Bài giảng Phương pháp tính - Chương 8: Xấp xỉ hàm số bằng đa thức đa thức nội suy Lagrange - Hà Thị Ngọc Yến
ĐA THỨC NỘI SUY
- Cho bộ điểm
- Đa thức bậc không quá n, đi qua
bộ điểm trên được gọi là đa thức nội suy
với các mốc nội suy
- Khi đó
xii n 0,ĐA THỨC NỘI SUY
• Định lý: Với bộ điểm
cho trước, đa thức nội suy tồn tại và duy
nhất

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5
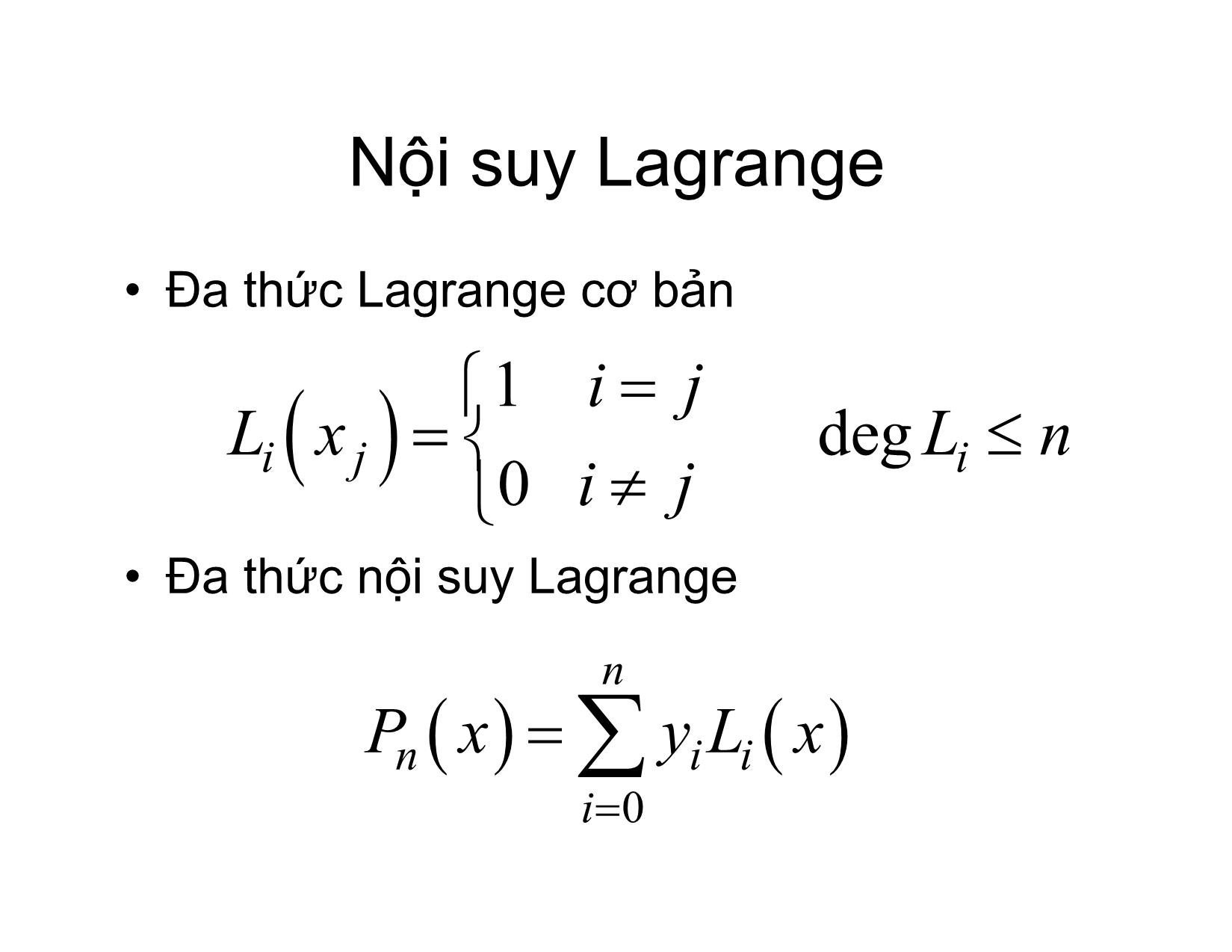
Trang 6
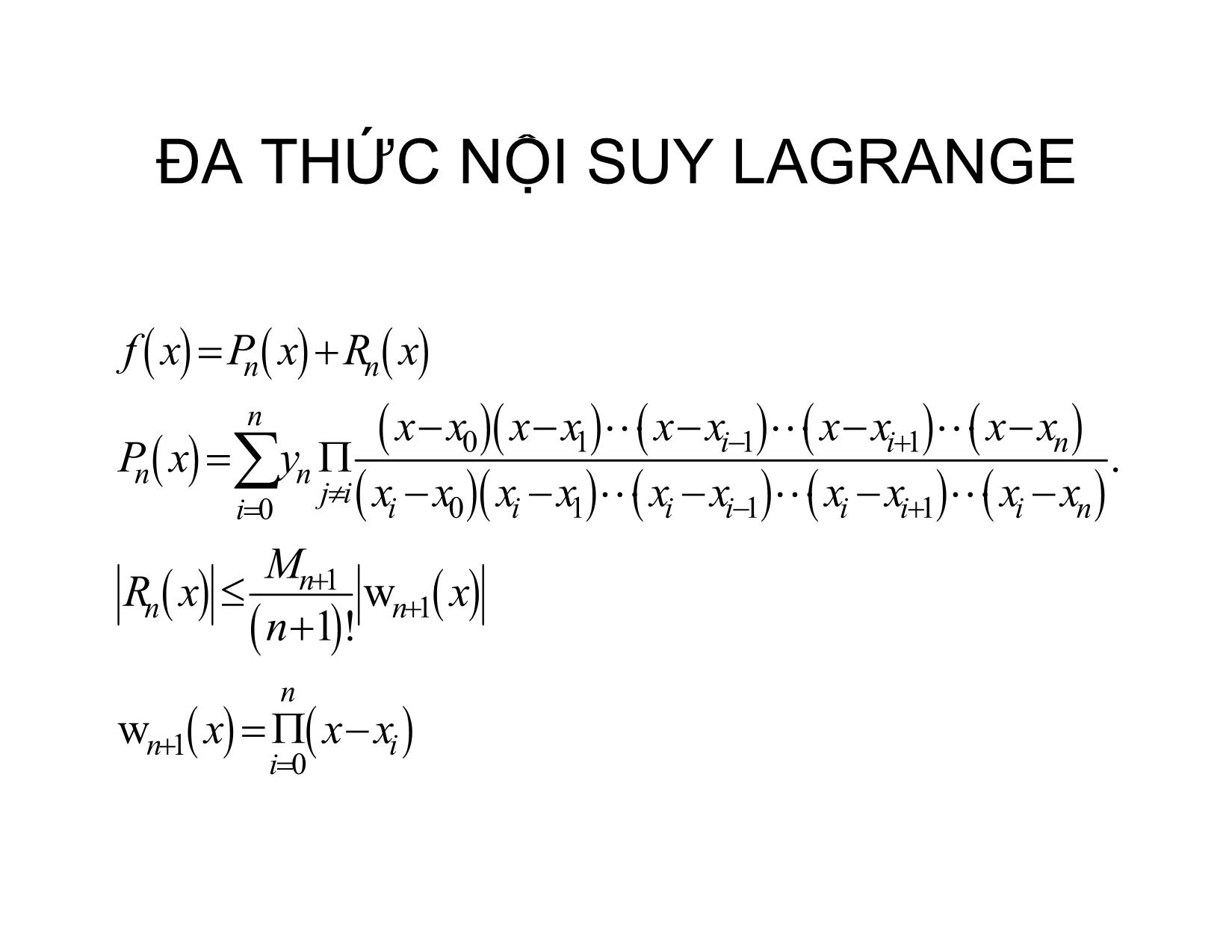
Trang 7

Trang 8
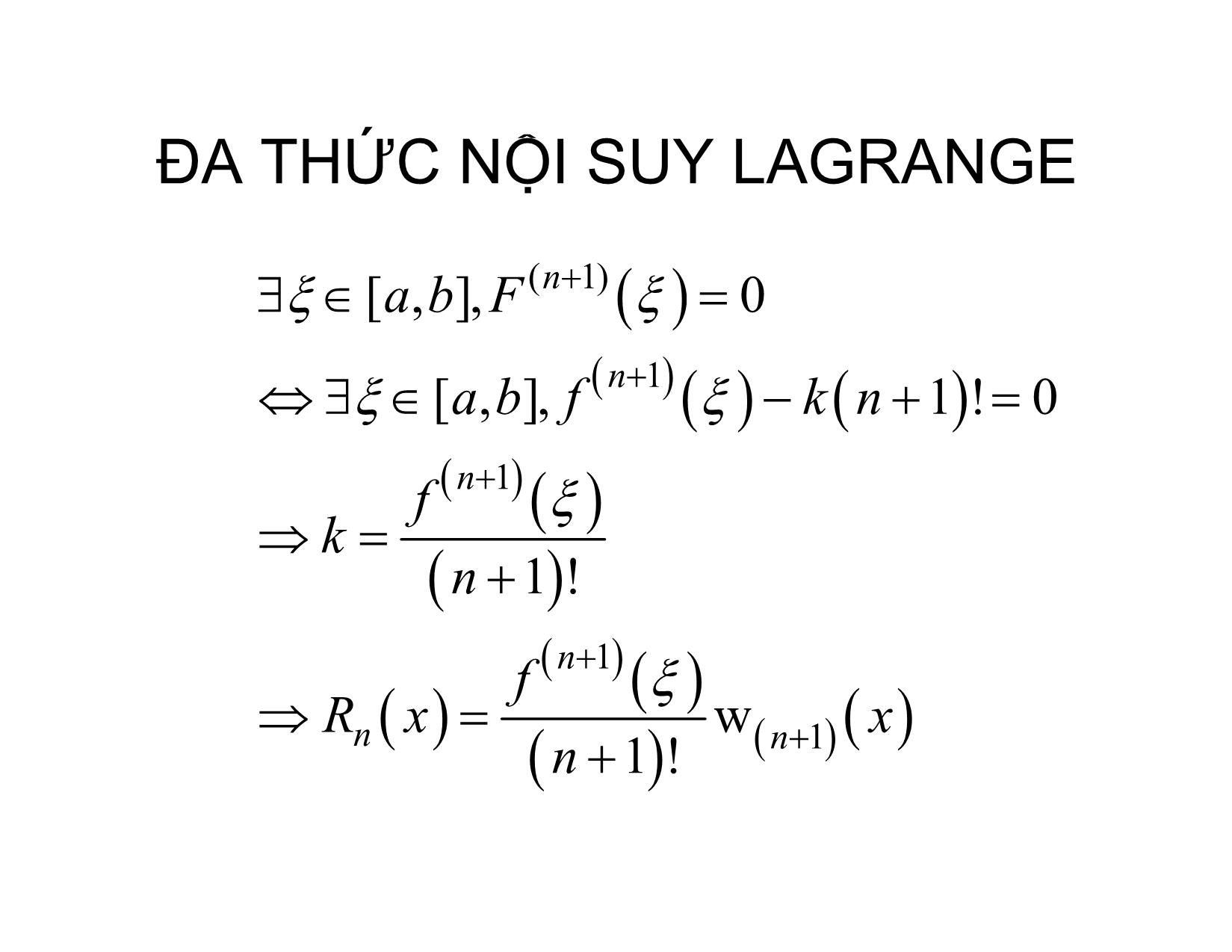
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Phương pháp tính - Chương 8: Xấp xỉ hàm số bằng đa thức đa thức nội suy Lagrange - Hà Thị Ngọc Yến", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Phương pháp tính - Chương 8: Xấp xỉ hàm số bằng đa thức đa thức nội suy Lagrange - Hà Thị Ngọc Yến

XẤP XỈ HÀM SỐ BẰNG ĐA THỨC ĐA THỨC NỘI SUY LAGRANGE Hà Thị NgọcYến Hà nội, 2/2017 ĐA THỨC NỘI SUY -Chobộđiểm x ,,,[,]yfx xxijxab ii i in 0, i j i - Đathứcbậc không quá n, Px n đi qua bộđiểmtrênđượcgọilàđathứcnộisuy x vớicácmốcnộisuy iin 0, -Khiđó f xPx n ĐA THỨC NỘI SUY x ,,yxxij , • Định lý: Vớibộđiểm iiin 0, i j cho trước, đathứcnộisuytồntạivàduy nhất ĐA THỨC NỘI SUY 2 n Pxnn a01 axax 2 ax aaxaxax 2 n y on10 20 0 0 2 n aaxaxaxon 11 21 1 y 1 Pxni y i i0, n 2 n aaxaxax y on12 n nnn ĐA THỨC NỘI SUY • Định thức n 1 xx00 n 1 xx11 xxij 0. ij n 1 xxnn •Vậyhệ có nghiệm duy nhất hay đathứcnộisuy tồntại và duy nhất Nội suy Lagrange • Đathức Lagrange cơ bản 1 ij Lij xLn deg i 0 ij • Đathứcnội suy Lagrange n Pxnii y Lx i 0 ĐA THỨC NỘI SUY LAGRANGE fx Pxnn Rx n xx 01 xx xx iin 1 xx 1 xx Pxnn y . ji i 0 xxxxii 01 xx iiiiin 1 xx 1 xx Mn 1 Rxnn w 1 x n 1! n wni 1 xxx i 0 ĐA THỨC NỘI SUY LAGRANGE • Đặt Ft Rnn t kw 1 t •Chọnk saocho Fx :0 fx Pnn x kw 1 x • F(t) có ít nhất n+2 nghiệm phân biệt nên F’(x) có ít nhất n+1 nghiệm phân biệt, .. ĐA THỨC NỘI SUY LAGRANGE (1)n [,],ab F 0 n 1 [,],ab f k n 1! 0 n 1 f k n 1! n 1 f Rxn w n 1 x n 1! ĐT NỘI SUY NEWTON x •Vídụ: xét hàm số y 3 x -1 0 1 y 1/3 1 3 ĐT NỘI SUY LAGRANGE xx 1 112 Lx1 x x 10 11 2 2 xx 11 2 Lx2 x 1 0101 xx 1 112 Lx3 x x 1110 2 2 1242 Lx L x L x31 L x x x 33312 3 ĐT NỘI SUY LAGRANGE 1110 fL 31.14 10 10
File đính kèm:
 bai_giang_phuong_phap_tinh_chuong_8_xap_xi_ham_so_bang_da_th.pdf
bai_giang_phuong_phap_tinh_chuong_8_xap_xi_ham_so_bang_da_th.pdf

