Bài giảng Phương pháp tính - Chương 7: Phương pháp Lặp đơn – Lặp Jacob giải phương trình ax=b - Hà Thị Ngọc Yến
Ý tưởng phương pháp
- Đưa về phương trình tương đương
- Lập dãy số
- Nếu dãy hội tụ thì giới hạn là nghiệm của
phương trình
Ax b x Bx d
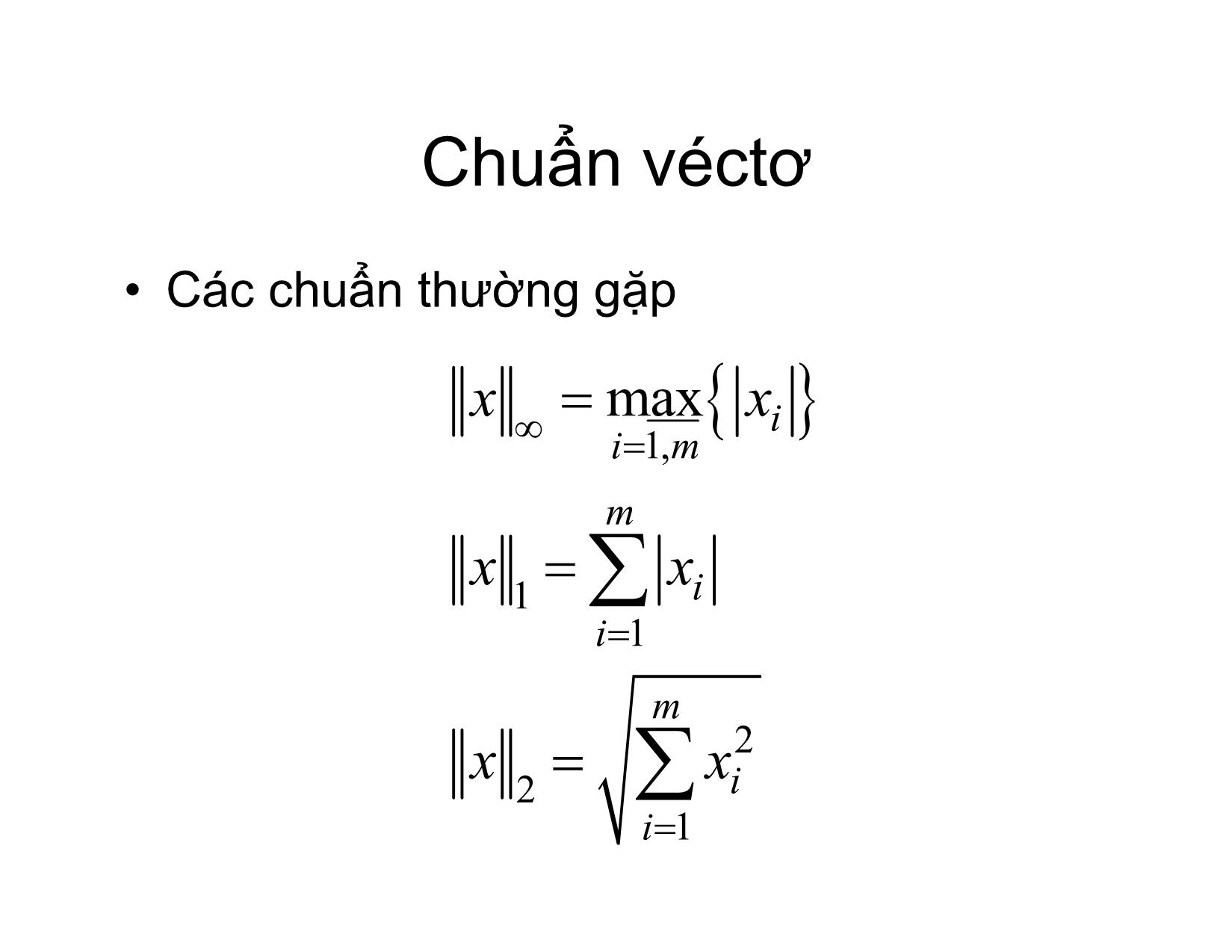
x Bx d x n n Chuẩn của véctơ
• Định nghĩa: chuẩn là một ánh xạ thỏa mãn
các tính chất sau

Trang 1

Trang 2

Trang 3
Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Phương pháp tính - Chương 7: Phương pháp Lặp đơn – Lặp Jacob giải phương trình ax=b - Hà Thị Ngọc Yến", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Phương pháp tính - Chương 7: Phương pháp Lặp đơn – Lặp Jacob giải phương trình ax=b - Hà Thị Ngọc Yến

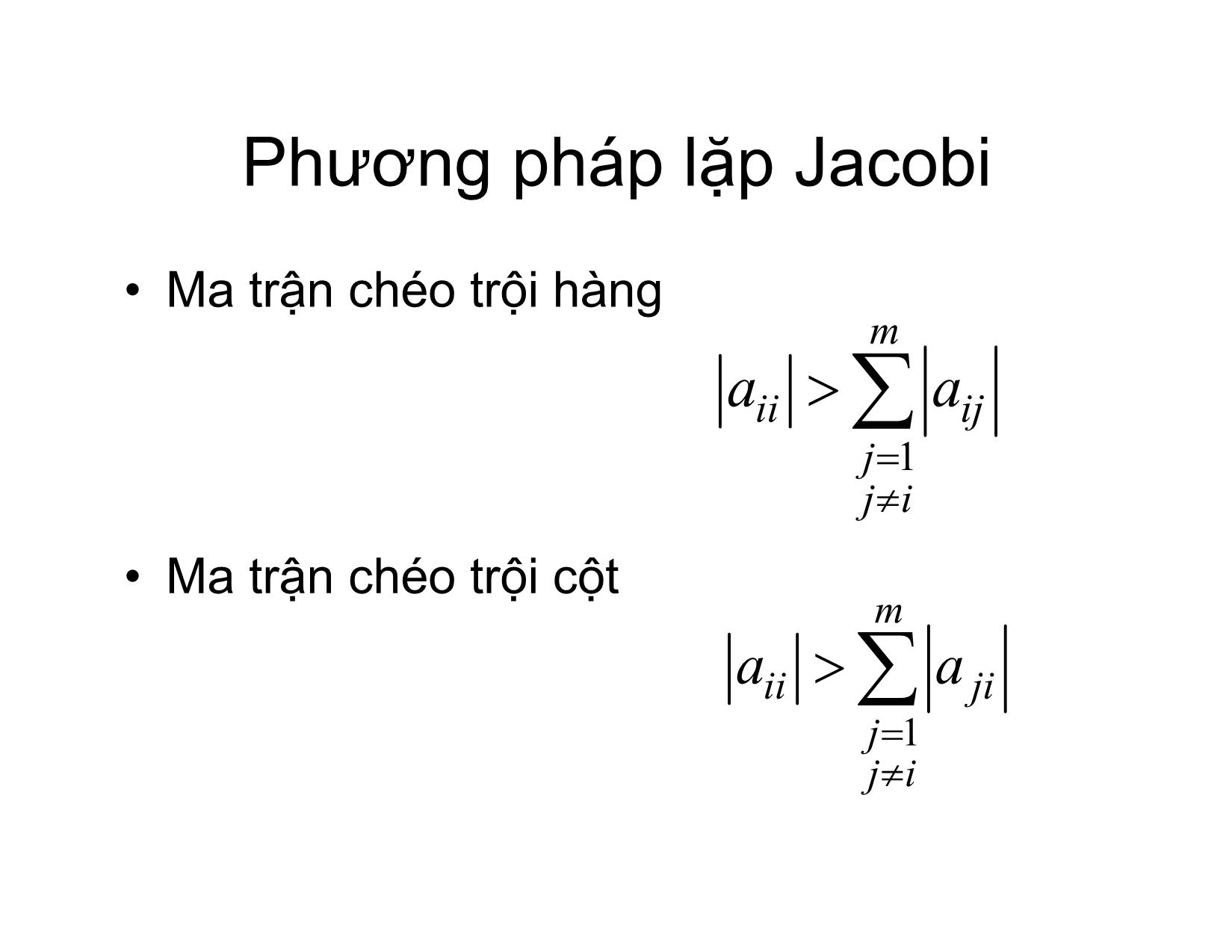
PP LẶP ĐƠN – LẶP JACOBI GIẢI PT Ax = b Hà Thị NgọcYến Hà nội, 2/2017 Ý tưởng phương pháp - Đưavề phương trình tương đương Ax b x Bx d -Lập dãy số m xBxdxnn 10, -Nếu dãy hộitụ thì giớihạn là nghiệmcủa phương trình Chuẩncủavéctơ • Định nghĩa: chuẩnlàmột ánh xạ thỏamãn các tính chấtsau: .:m uu 0, " " 0 ku k u k u m uv u v Chuẩnvéctơ •Cácchuẩnthường gặp xx max i im 1, m xx 1 i i 1 m xx 2 2 i i 1 Sự hộitụ của dãy véctơ • Định nghĩa: nn xxxxnn **0 n xximni i *1, •Chuẩntương đương: Hai chuẩnp vàq đượcgọilàtương đương nếu CC,0, C x x C x 12 1p qp 2 Sự hộitụ của dãy véctơ •Nếu hai chuẩnp vàq tương đương thì dãy véctơ hộitụ theo chuẩnp khivàchỉ khinóhộitụ theo chuẩnq •Mọichuẩn trong không gian véctơ hữu hạnchiều đềutương đương Chuẩncủa ma trận Ax AAx supp sup ppx xx 01p p m Aa max ij im 1, j 1 m Aa max 1 ij jm 1, i 1 AAA max T 2 i Sự hộitụ củaPP lặp đơn •NếuthìdãyB 1 xBxdxnn 10 , hộitụ tới nghiệm đúng duy nhấtcủaphương trìnhx Bx d theo đánh giá B n xx * xx n 1 B 10 B xx * xx nnn1 B 1 Các bướccm sự hộitụ củaPP • Dãy xn là dãy Cauchy nên hộitụ •Giớihạncủa dãy là nghiệm duy nhấtcủa phương trình • Cm hai công thứcsaisố Phương pháp lặp Jacobi •Ma trậnchéotrội hàng m aaii ij j 1 ji •Ma trậnchéotrộicột m aa ii ji j 1 ji PP lặp Jacobi • A là ma trậnchéotrội hàng: ab a 0 12 1m 1 aa a 11 11 11 a ab 21 0 22m Bd aa; a 22 22 22 aa b mm12 0 m aamm mm amm PP lặp Jacobi • A là ma trậnchéotrộicột: 1 00 a xy 11 11 1 xy00 22 a 22 xymm 1 00 amm Lặp Jacobi • A là ma trậnchéotrộicột: a a 0 12 1m aa 22 mm b a a 1 21 0 2m b Bd aa; 2 11 mm b aa m mm12 0 aa11 22
File đính kèm:
 bai_giang_phuong_phap_tinh_chuong_7_phuong_phap_lap_don_lap.pdf
bai_giang_phuong_phap_tinh_chuong_7_phuong_phap_lap_don_lap.pdf

