Bài giảng Phương pháp tính - Chương 6: Phương pháp Gauss và Gauss-Jordan giải phương trình ax=b - Hà Thị Ngọc Yến
Phương pháp Gauss
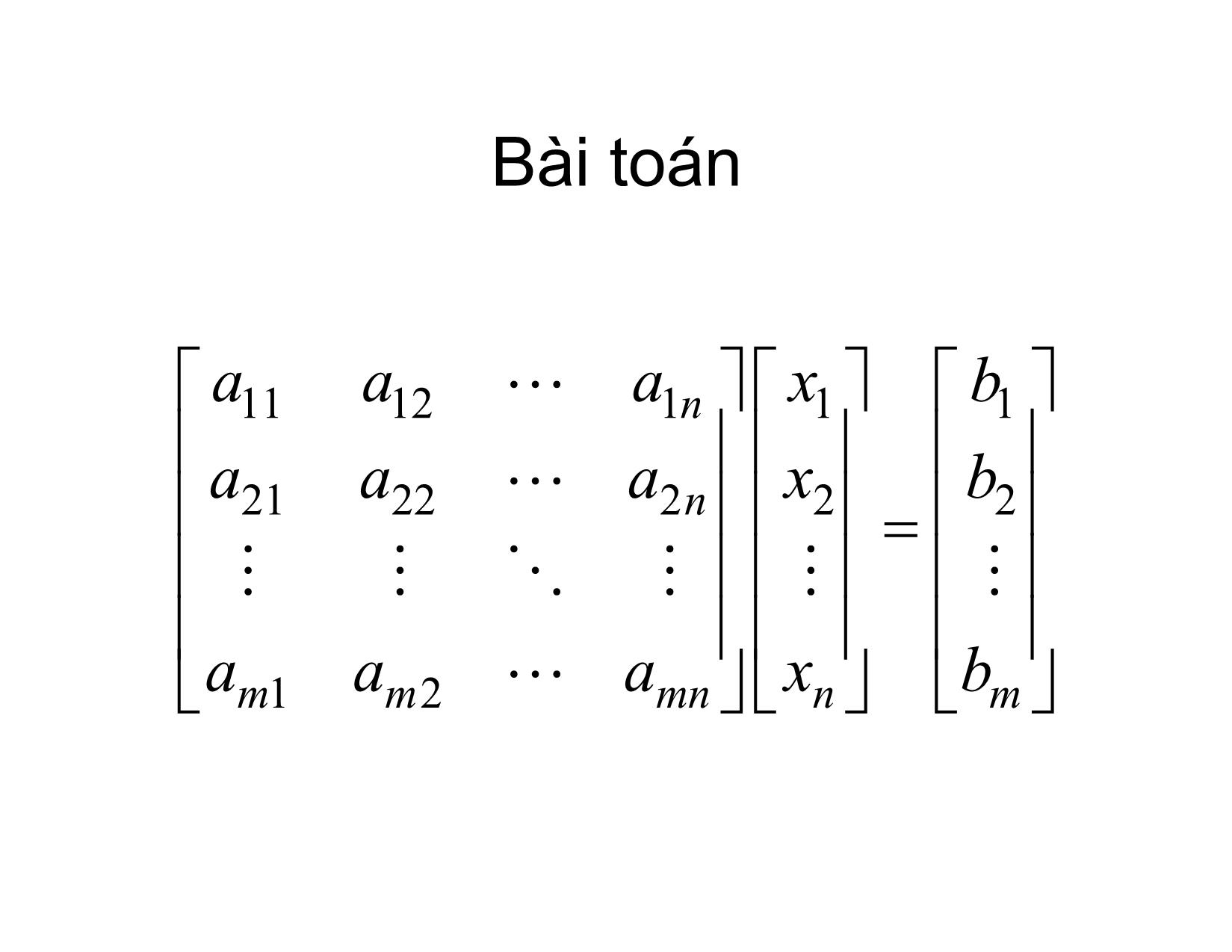
Ý tưởng:
• Quy trình thuận (QTT): Dùng phép khử dần
ẩn khỏi các phương trình đề đưa ma trận bổ
sung về dạng bậc thang.
• Quy trình nghịch (QTN): Dùng phép thế từ hệ
bậc thang để tìm dần giá trị các ẩn

Trang 1
Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9

Trang 10
Bạn đang xem tài liệu "Bài giảng Phương pháp tính - Chương 6: Phương pháp Gauss và Gauss-Jordan giải phương trình ax=b - Hà Thị Ngọc Yến", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Phương pháp tính - Chương 6: Phương pháp Gauss và Gauss-Jordan giải phương trình ax=b - Hà Thị Ngọc Yến

PP GAUSS VÀ GAUSS-JORDAN GIẢI PT Ax = b Hà Thị NgọcYến Hà nội, 3/2018 Bài toán aa11 12 ax 1n 1 b 1 aa ax b 21 22 2n 2 2 aamm12 a mnn x b m Phương pháp Gauss Ýtưởng: • Quy trình thuận (QTT): Dùng phép khử dần ẩnkhỏi các phương trình đề đưa ma trậnbổ sung về dạng bậc thang. • Quy trình nghịch (QTN): Dùng phép thế từ hệ bậc thang để tìm dần giá trị các ẩn. PP Gauss – QTT •B1: Khởitạo ijind 1; 1; [0,0,....,0]1 m •B2:Kiểmtra nếu aindijij 0 B3, trái lại thì sang B6 •B3: Nếuthìkim ết thúc QTT Nếu không, thì sang B4 • B4: Cho k chạytừ i+1 đến m, thựchiện biến đổi akj LLLkik aij PP Gauss - QTT •B5: Nếujn thì QTT kết thúc, trái lại ii 1; j j 1 B2 • B6: Cho ti 1. •B7: Kiểmtra nếuthìatj 0 đổichỗ 2 hàng t và i, vàind i j B3, trái lại sang B8 •B8: Nếutmjn ; thì QTT kết thúc NếuthìB2,tmjn ; jj 1 Nếutm thìtt 1 B7 PP Gauss - QTN Dành cho các bạntự viết Phương pháp Gauss - Jordan Ýtưởng: •Hạnchế sai số tính toán khi gặp các phép chia cho số gần0 bằng cách chọnphầntử khử thích hợp • Dùng phép khửẩnthứ k (tương ứng với cộtcóchứaphầntử khử) khỏitấtcả các hàng không chứaphầntử khử Chọnphầntử khử • Ưu tiên 1: k Chọn a 1;2;4;5... để các phép chia pq k choapq không có sai số hoặcsaisố nhỏ. • Ưu tiên 2: k kk 1 Chọnsaochoapq aapq max i, j ij •Chúý: Phầntử khử thứ k đượcchọntừ các hàng và cột không chứa các phầntử khửđãchọntrước đó. Quá trình khử Cho t chạytừ 1 đến m, tp , thựchiện phép biến đổi atq LLLtpt apq Quá trình khử aa11... 0 ... a 1 1 aa11 12... a 1qn ... a 1 b 11 12 1n b 1 1 11 1 1 aa21 22... a 2qn ... a 2 b aa... 0 ... a b 2 21 22 2n 2 ... ... ... ... aap12 p... a pq ... a pn bp aa... a ... a bp pp12 pqpn ... ... b 1 111 aam12 m... a mq ... a mn m aa... 0 ... a b m1 mmn2 m
File đính kèm:
 bai_giang_phuong_phap_tinh_chuong_6_phuong_phap_gauss_va_gau.pdf
bai_giang_phuong_phap_tinh_chuong_6_phuong_phap_gauss_va_gau.pdf

