Bài giảng Phương pháp tính - Chương 11: Tính gần đúng tích phân xác định - Hà Thị Ngọc Yến
PP HÌNH THANG
• Chia đoạn lấy tích phân thành n phần
bằng nhau
PP SIMPSON (PARABOL)
• Chia đoạn lấy tích phân thành 2n phần
bằng nhau

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6
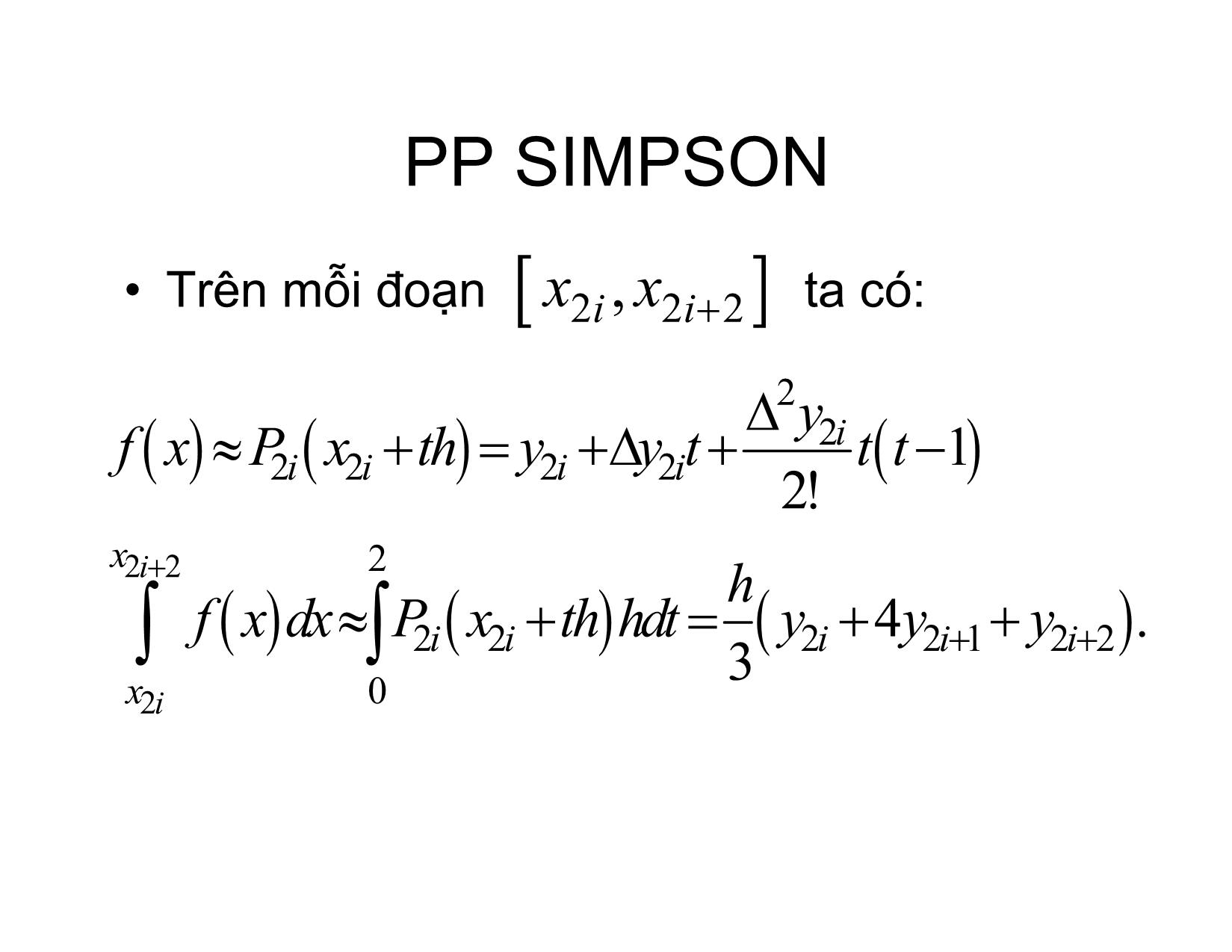
Trang 7

Trang 8
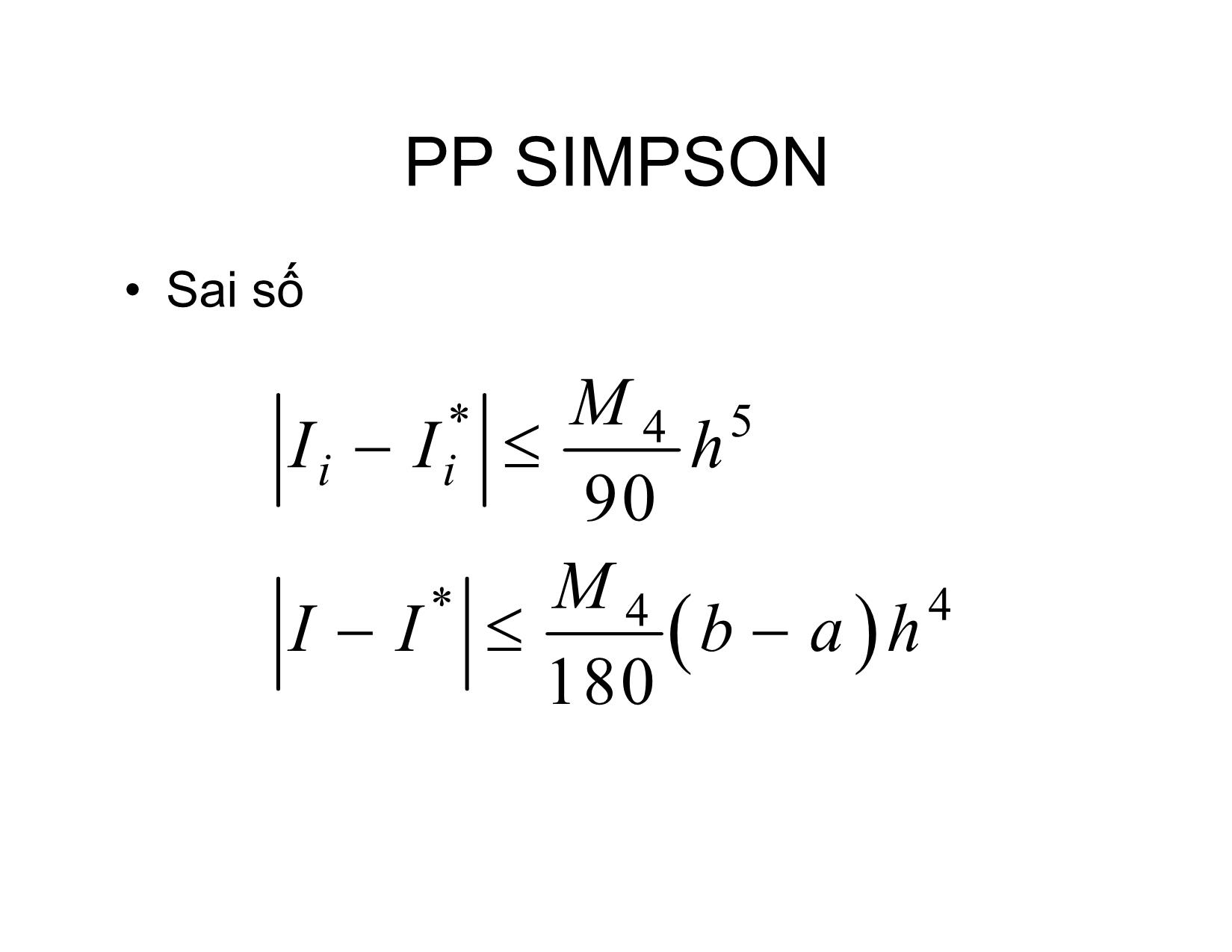
Trang 9
Bạn đang xem tài liệu "Bài giảng Phương pháp tính - Chương 11: Tính gần đúng tích phân xác định - Hà Thị Ngọc Yến", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Phương pháp tính - Chương 11: Tính gần đúng tích phân xác định - Hà Thị Ngọc Yến

TÍNH GẦN ĐÚNG TÍCH PHÂN XÁC ĐỊNH Hà Thị NgọcYến Hà nội, 2/2017 Ý tưởng f xPx n bb f xdx Pn xdx aa PP HÌNH THANG •Chiađoạnlấy tích phân thành n phần bằng nhau ab,, x01 x x 12 , x xnn 1 , x PP HÌNH THANG •Trênmỗi đoạntacó:xxii, 1 fx Px11iiiii y fxx , x x xx ii 11h fxdx Pxdx11iii y y . 2 xxii PP HÌNH THANG • Công thức tính: b h f xdx yy22 y y 2 01nn 1 a •Saisố: *3M 2 IIii h 12 *2M I Ibah2 12 PP SIMPSON (PARABOL) •Chiađoạnlấy tích phân thành 2n phần bằng nhau ax 012 x x x 2n b xxkhk 0 PP SIMPSON •Trênmỗi đoạntacó:xx222ii, 2 y2i fx P x thy yt tt 1 22ii 2 i 2 i 2! x 22i 2 h f x dx P x th hdt y4. y y 22ii3 2 i 2122 i i x2i 0 PP SIMPSON • Công thức tính: b h f xdx y42 y 3 0122n a 113 yy y 21n 224 yy y 22n PP SIMPSON •Saisố M II *54 h ii 90 M II *44 bah 180
File đính kèm:
 bai_giang_phuong_phap_tinh_chuong_11_tinh_gan_dung_tich_phan.pdf
bai_giang_phuong_phap_tinh_chuong_11_tinh_gan_dung_tich_phan.pdf

