Bài giảng Nguyên lý máy - Chương 4: Cân bằng máy - Nguyễn Chí Hưng
Lực quán tính xuất hiện khi nào?
Biến thiên theo chu kỳ hoạt động của máy
Khi v, ω >> Fqt >> Ptĩnh
Đặc điểm lực quán tính ly tâm
Tăng lực ma sát trong các khớp động dẫn tới giảm hiệu suất
của máy.
Làm rung động máy và nền móng dẫn tới giảm độ chính xác và
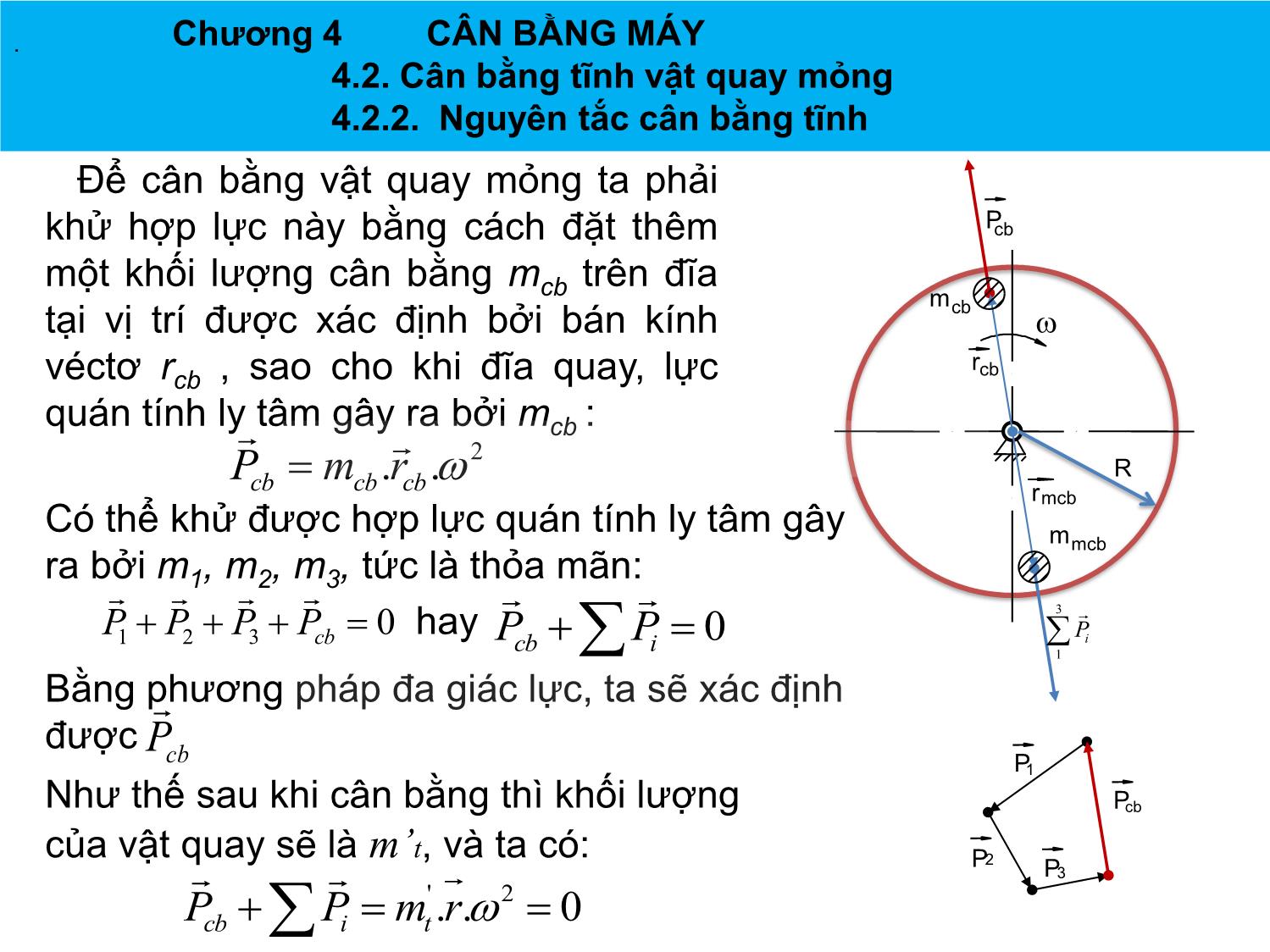
tuổi thọ của máy cũng nhƣ chất lƣợng sản phẩm.
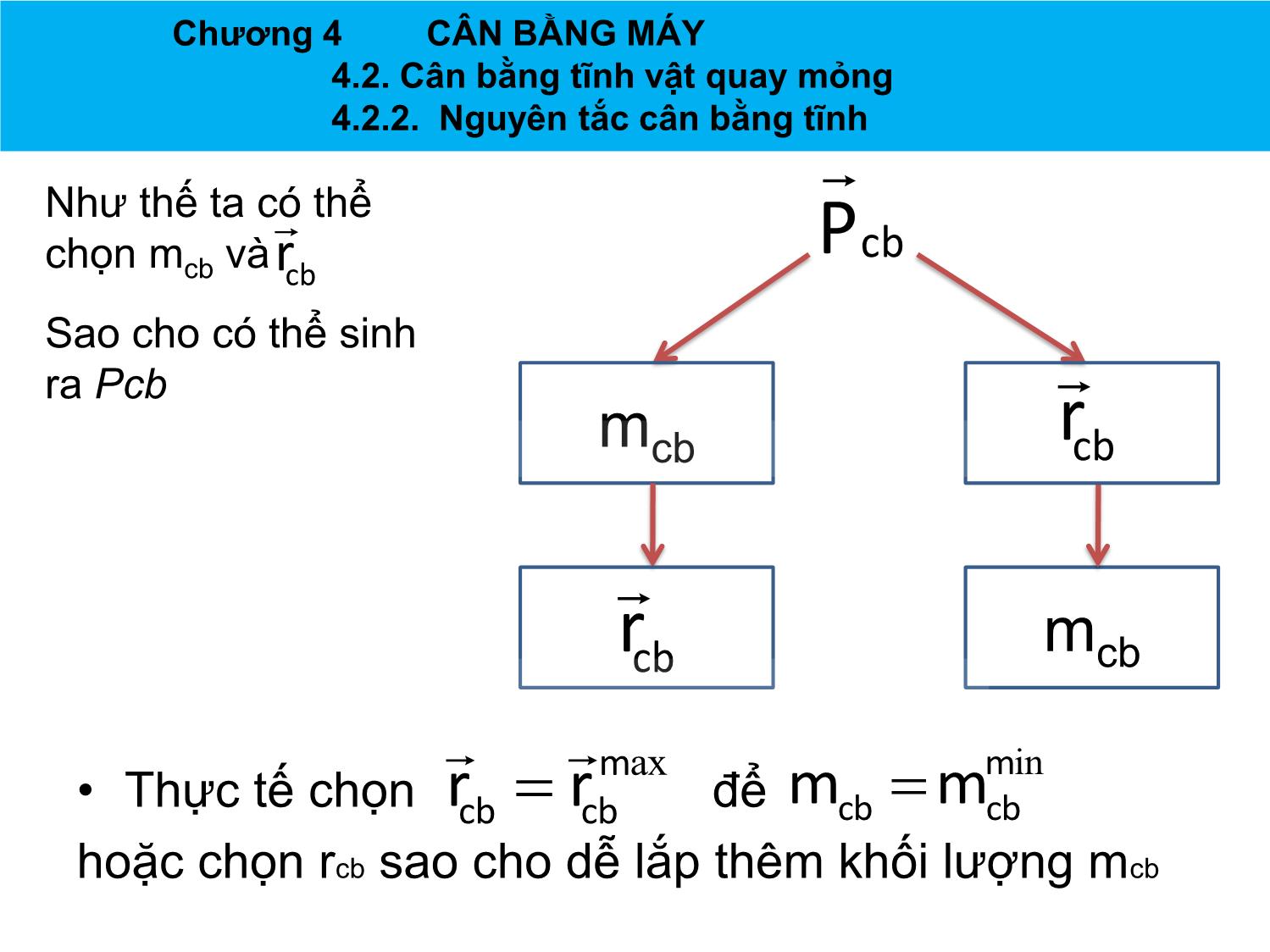
Ảnh hƣởng xấu đến môi trƣờng xung quanh và cả sức khỏe
của công nhân đứng máy.

Trang 1
Trang 2

Trang 3

Trang 4
Trang 5
Trang 6
Trang 7
Trang 8
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Nguyên lý máy - Chương 4: Cân bằng máy - Nguyễn Chí Hưng", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Nguyên lý máy - Chương 4: Cân bằng máy - Nguyễn Chí Hưng

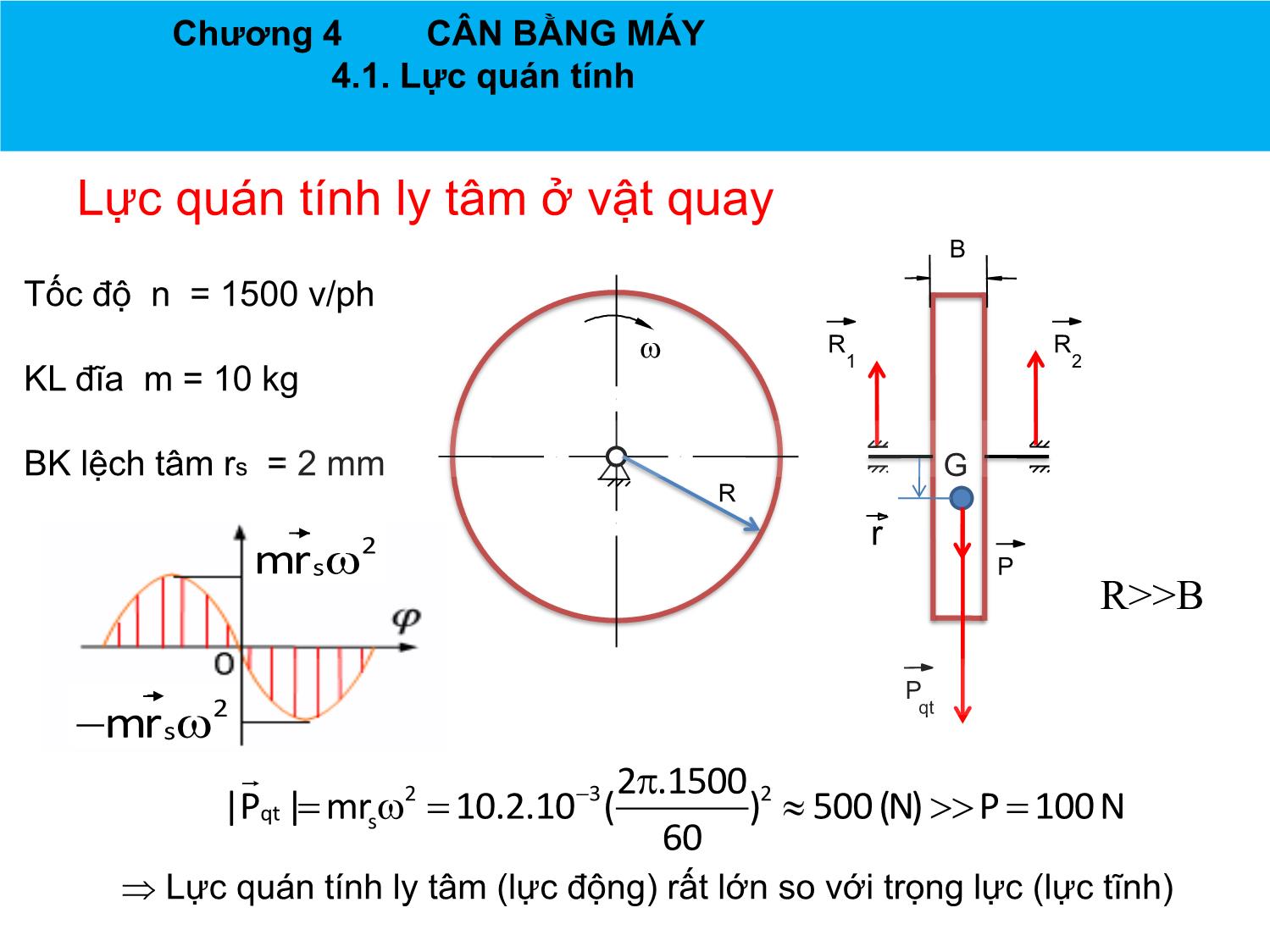
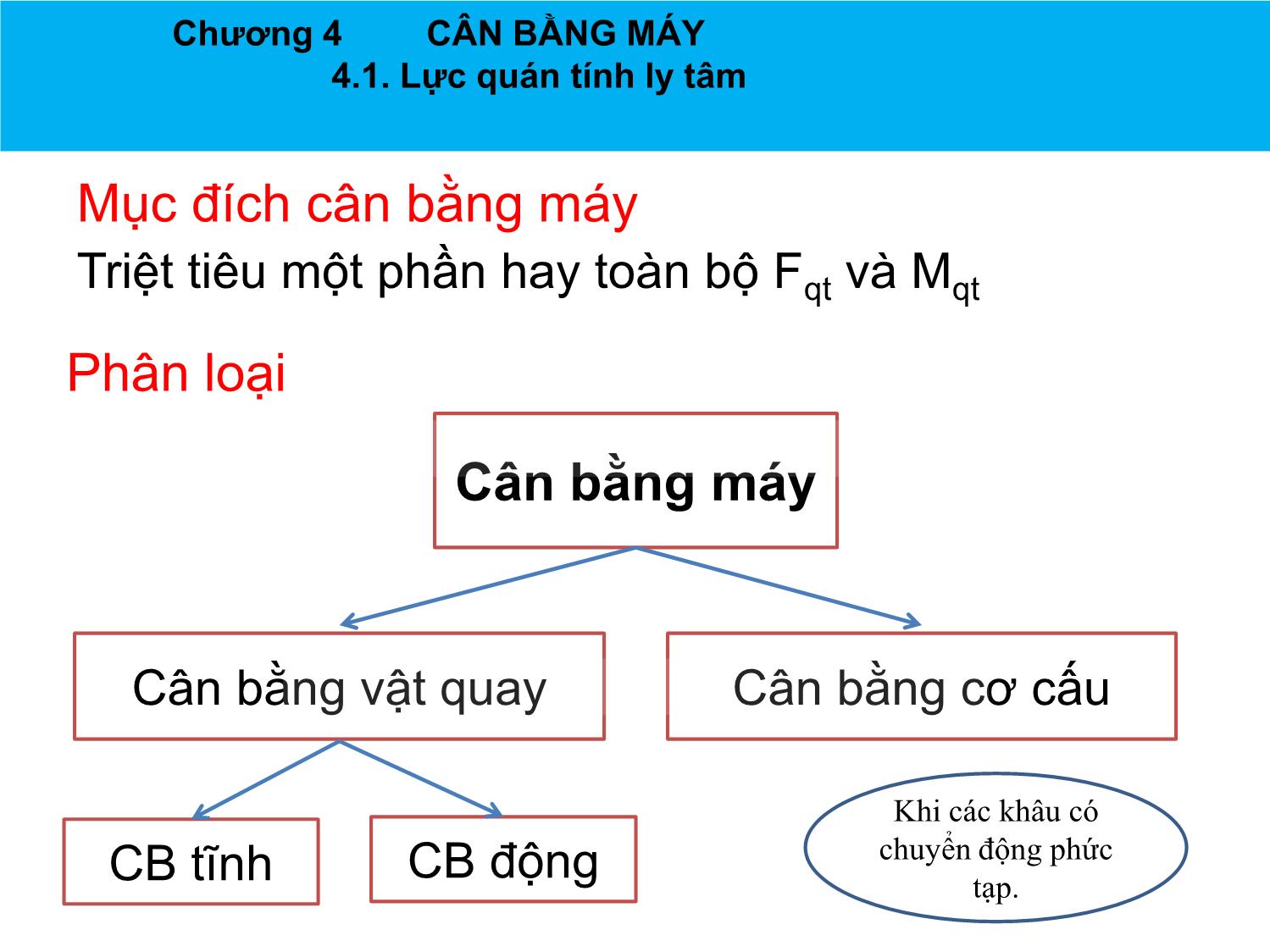
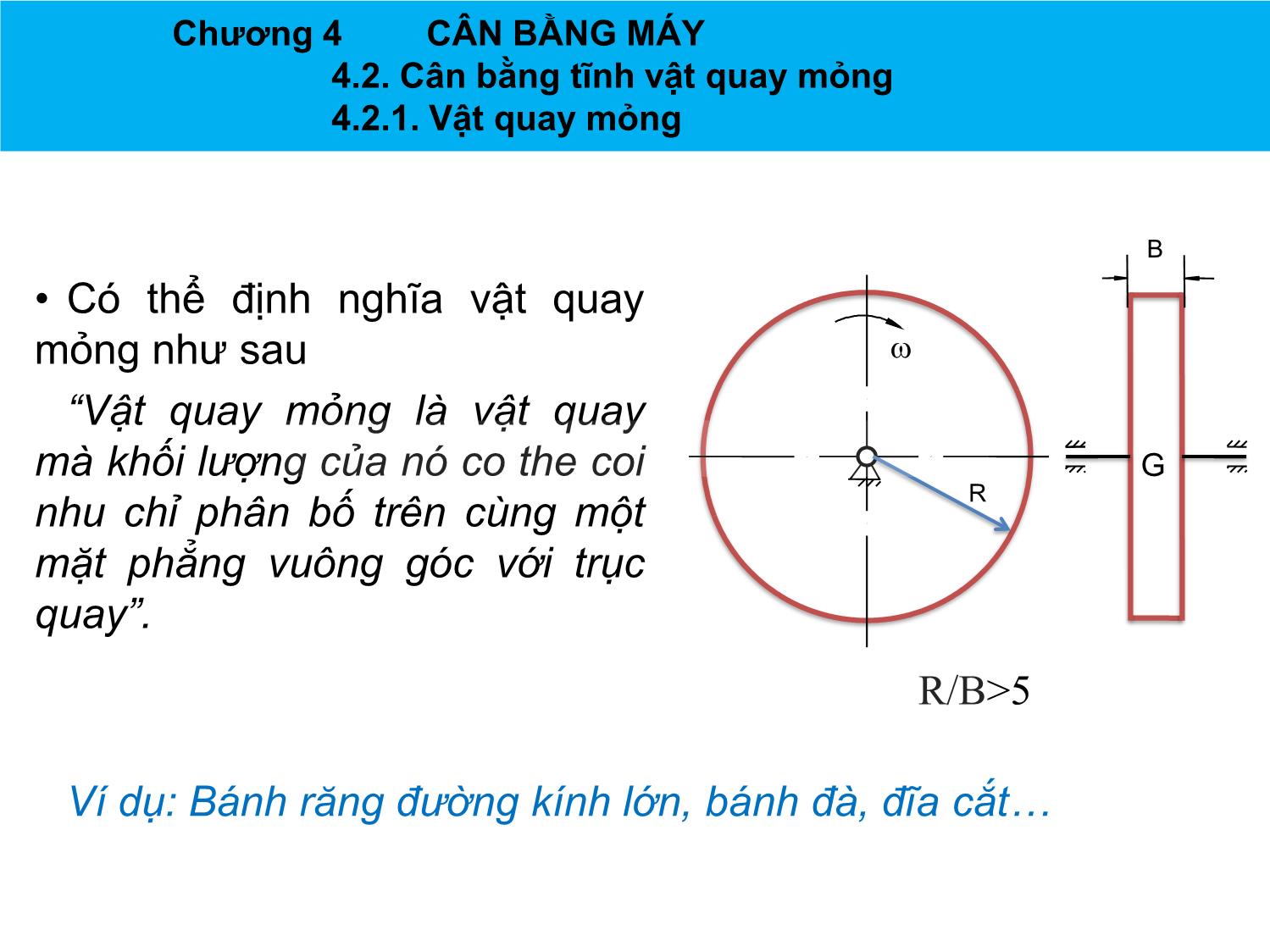
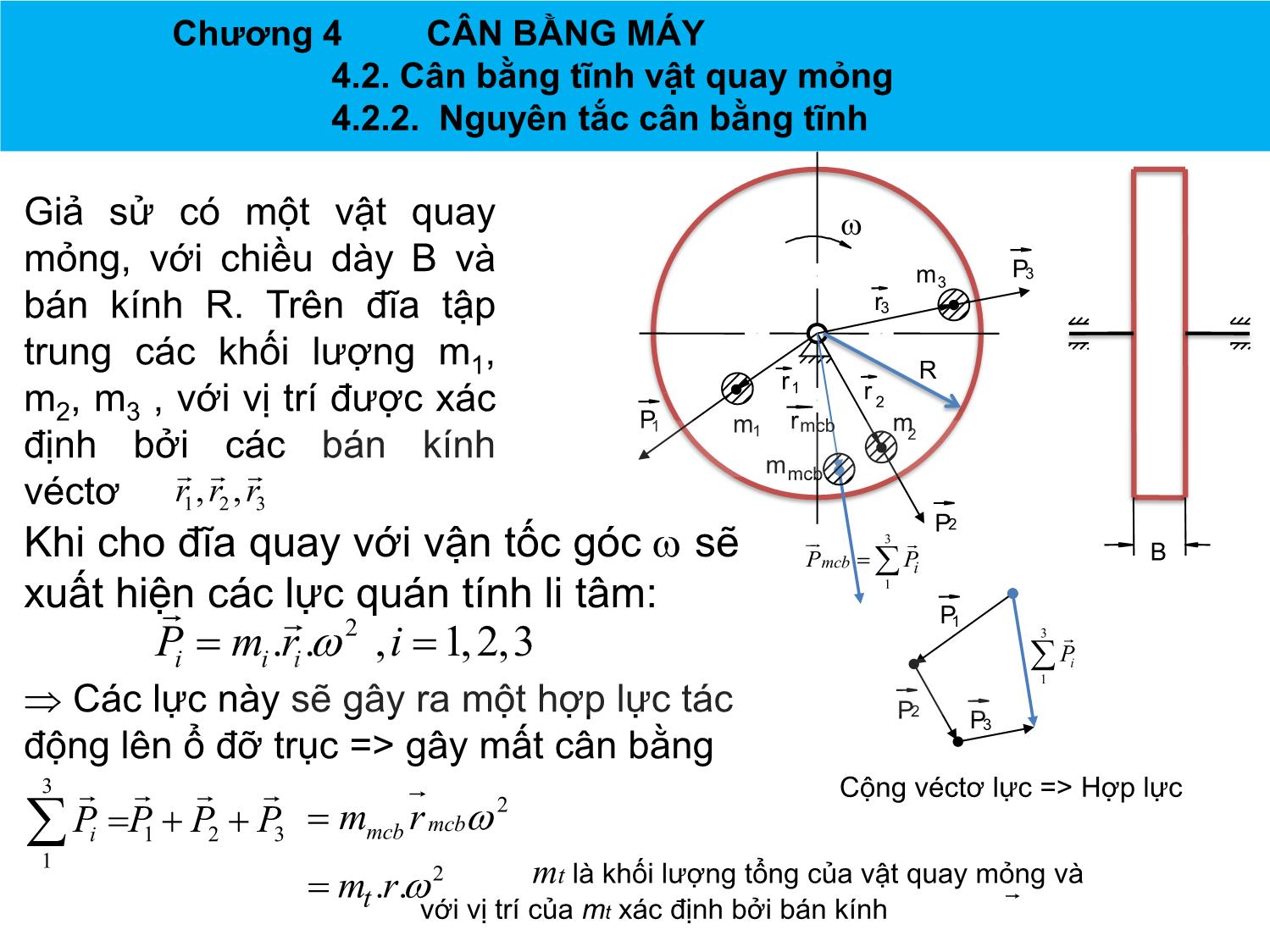
CHƢƠNG 4 CÂN BẰNG MÁY Chương 4 CÂN BẰNG MÁY 4.1. Lực quán tính Lực quán tính ly tâm ở vật quay B Tốc độ n = 1500 v/ph R R w 1 2 KL đĩa m = 10 kg BK lệch tâm rs = 2 mm G R 2 r mr sw P R>>B P 2 qt wmr s 2 32 .1500 2 |Pqt | mr w 10.2.10 ( ) 500(N) P 100N s 60 Lực quán tính ly tâm (lực động) rất lớn so với trọng lực (lực tĩnh) Chương 4 CÂN BẰNG MÁY 4.1. Lực quán tính Chương 4 CÂN BẰNG MÁY 4.1. Lực quán tính Lực quán tính xuất hiện khi nào? Máy là một cơ hệ chuyển động có gia tốc, vì vậy khi làm việc, trừ những khâu tịnh tiến đều hoặc quay đều với tâm quay trùng với trọng tâm, thì ở các khâu còn lại đều có lực quán tính hoặc quán tính ly tâm tác động. Đặc điểm lực quán tính ly tâm . Biến thiên theo chu kỳ hoạt động của máy . Khi v, ω >> Fqt >> Ptĩnh Tác hại . Tăng lực ma sát trong các khớp động dẫn tới giảm hiệu suất của máy. . Làm rung động máy và nền móng dẫn tới giảm độ chính xác và tuổi thọ của máy cũng nhƣ chất lƣợng sản phẩm. . Ảnh hƣởng xấu đến môi trƣờng xung quanh và cả sức khỏe của công nhân đứng máy. Chương 4 CÂN BẰNG MÁY 4.1. Lực quán tính ly tâm Mục đích cân bằng máy Triệt tiêu một phần hay toàn bộ Fqt và Mqt Phân loại Cân bằng máy Cân bằng vật quay Cân bằng cơ cấu Khi các khâu có CB động chuyển động phức CB tĩnh tạp. Chương 4 CÂN BẰNG MÁY 4.2. Cân bằng tĩnh vật quay mỏng 4.2.1. Vật quay mỏng B • Có thể định nghĩa vật quay mỏng nhƣ sau w “Vật quay mỏng là vật quay mà khối lượng của nó co the coi G nhu chỉ phân bố trên cùng một R mặt phẳng vuông góc với trục quay”. R/B>5 Ví dụ: Bánh răng đường kính lớn, bánh đà, đĩa cắt Chương 4 CÂN BẰNG MÁY 4.2. Cân bằng tĩnh vật quay mỏng 4.2.2. Nguyên tắc cân bằng tĩnh Giả sử có một vật quay w mỏng, với chiều dày B và P3 m3 bán kính R. Trên đĩa tập r3 trung các khối lƣợng m1, R r1 r m2, m3 , với vị trí đƣợc xác 2 P1 m rmcb m định bởi các bán kính 1 2 mmcb véctơ r1,, r 2 r 3 P2 3 Khi cho đĩa quay với vận tốc góc w sẽ B PPmcb i xuất hiện các lực quán tính li tâm: 1 P1 P m. r .w2 , i 1,2,3 3 i i i Pi 1 Các lực này sẽ gây ra một hợp lực tác P2 P3 động lên ổ đỡ trục => gây mất cân bằng 3 Cộng véctơ lực => Hợp lực 2 mrmcbw PPPPi 1 2 3 mcb 1 2 mt là khối lƣợng tổng của vật quay mỏng và mrt..w với vị trí của mt xác định bởi bán kính r . Chương 4 CÂN BẰNG MÁY 4.2. Cân bằng tĩnh vật quay mỏng 4.2.2. Nguyên tắc cân bằng tĩnh Để cân bằng vật quay mỏng ta phải khử hợp lực này bằng cách đặt thêm Pcb một khối lƣợng cân bằng m trên đĩa cb m tại vị trí đƣợc xác định bởi bán kính cb w r véctơ rcb , sao cho khi đĩa quay, lực cb quán tính ly tâm gây ra bởi mcb : 2 R Pcb m cb.. r cb w rmcb Có thể khử đƣợc hợp lực quán tính ly tâm gây mmcb ra bởi m , m , m , tức là thỏa mãn: 1 2 3 3 PPPP1 2 3 cb 0 hay PP 0 Pi cb i 1 Bằng phƣơng pháp đa giác lực, ta sẽ xác định đƣợc Pcb P1 Nhƣ thế sau khi cân bằng thì khối lƣợng Pcb của vật quay sẽ là m’t, và ta có: P2 P3 '2 Pcb P i m t . r .w 0 Chương 4 CÂN BẰNG MÁY 4.2. Cân bằng tĩnh vật quay mỏng 4.2.2. Nguyên tắc cân bằng tĩnh Nhƣ thế ta có thể chọn m và Pcb cb rcb Sao cho có thể sinh ra Pcb mcb rcb rcb mcb max min • Thực tế chọn rrcb cb để mmcb cb hoặc chọn rcb sao cho dễ lắp thêm khối lƣợng mcb Chương 4 CÂN BẰNG MÁY 4.2. Cân bằng tĩnh vật quay mỏng 4.2.2. Nguyên tắc cân bằng tĩnh Nhận xét: . Cần ít nhất một đối trọng (Có thể thêm nhiều đối trọng) Chú ý : . Có thể không cần thêm khối lƣợng mcb nhƣ đã làm, mà bớt đi một khối lƣợng mcb ở vị trí đối tâm với điểm ngọn của véctơ rcb để cho đĩa cân bằng (khoan lỗ trên đĩa). . Thay vì thêm một đối trọng, ta có thể thêm hai, ba... đối trọng với điều kiện hợp lực của các lực quán tính li tâm do chúng gây ra phải bằng Pcb . Chương 4 CÂN BẰNG MÁY 4.2. Cân bằng tĩnh vật quay mỏng 4.2.3. Thí nghiệm cân bằng tĩnh • Vật quay nào có trạng thái cân bằng tĩnh? (Trạng thái cân bằng phiếm định). B R Có trục quay đi qua trọng tâm của vật quay. Như thế khi quay, lực quán tính ly tâm của vật quay có giá0.bằng trị Chương 4 CÂN BẰNG MÁY 4.2. Cân bằng tĩnh vật quay mỏng 4.2.3. Thí nghiệm cân bằng tĩnh Lƣợng gắn thêm Đặt 2 đầu trục quay của đĩa cần cân bằng lên 2 lƣỡi dao nằm ngang và song song với nhau m hoặc lên giá đỡ có 2 ổ bi với mục đích để giảm ma sát giữa trục và giá đỡ. Nếu đĩa cân bằng thì nó sẽ không lăn và nằm im ở mọi vị trí (trạng thái cân bằng phiếm định). Còn nếu đĩa chƣa cân bằng thì nó sẽ lăn cho đến khi trọng Khoan bớt m tâm của nó nằm ở vị trí thấp nhất (trạng thái cân bằng bền). Nhƣ vậy ta cần thực hiện thí nghiệm đến khi đĩa ở trạng thái cân bằng phiếm định, tức là lúc đó mô men gây ra bởi trọng lƣợng đĩa với tâm quay bằng 0. Nhƣ thế vị trí trọng tâm của đĩa đƣợc đƣa về tâm quay. => Để triệt tiêu lực quán tính ly tâm ở vật quay mỏng, ta có thể thực hiện thí nghiệm ở trạng thái tĩnh, vật cần cân bằng không cần phải quay trên trục thí nghiệm cân bằng tĩnh Chương 4 CÂN BẰNG MÁY 4.2. Cân bằng tĩnh vật quay mỏng 4.2.3. Thí nghiệm cân bằng tĩnh Để đƣa đĩa về trạng thái cân bằng phiếm định, ta dùng mát-tít đắp dần lên phần cao nhất của Lƣợng gắn thêm đĩa và nằm trên đƣờng tròn bán m kính r nào đó để dễ đắp matít. Vừa làm vừa thử cho đến khi đạt đƣợc trạng thái cân bằng phiếm định. Sau đó ta lấy lƣợng mát-tít vừa đắp ra để cân, để biết khối lƣợng tổng của lƣợng matít đắp vào. Tiếp theo ta gắn vào vị trí vừa lấy ra đối trọng với Khoan bớt m khối lƣợng tƣơng đƣơng. Ta cũng có thể khoan bớt một lƣợng kim loại ở vị trí đối xứng qua tâm để làm cho đĩa cân bằng. (chọn vị trí dễ khoan và không ảnh hƣởng đến độ bền của đĩa) Chương 4 CÂN BẰNG MÁY 4.2. Cân bằng tĩnh vật quay mỏng 4.2.3. Thí nghiệm cân bằng tĩnh Chương 4 CÂN BẰNG MÁY 4.2. Cân bằng tĩnh vật quay mỏng 4.2.3. Thí nghiệm cân bằng tĩnh R1 Chia các tia các nhau 5 độ, chia càng nhỏ Mms độ chính xác càng cao Vẽ đƣờng tròn bán kính R1, gắn các khối mi lƣợng mi tƣơng ứng với tia i, tăng dần khối lƣợng mi đến khi vật bắt đầu quay. (Mms - P.r.cos ) - Qi.R1 = 0 Mms Cân mi ta sẽ tìm thấy mmax và mmin r Yêu cầu kiểm nghiệm tới khi nào tia Với Qi = mi.g R1 Qi chứa mmax và mmin phải tạo một góc P 1800 khi đó cos = 1 Mms Mms = Qmax.R1 - P.r r R1 r Mms = Qmin.R1 + P.r P Mms Qmax R1 P Qmin => r = (Qmax - Qmin)R1/2.P Như thế khi biết r thì có thể thêm một lượng gắn lên tia chứa mmax ở vị trí có bán kính thích hợp để vật quay cân bằng hơn. Chương 4 CÂN BẰNG MÁY 4.3. Cân bằng động vật quay dày 4.3.1. Lý do phải cân bằng động Xét vật có 2 khối lƣợng m1 và m2 phân bố trên cùng 2 mặt phẳng khác nhau vuông góc với trục quay và đồng thời cùng nằm trên 1 mặt phẳng chứa trục quay, và ở 2 phía khác nhau đối với trục, vị trí của m1, m2 đƣợc xác định bởi hai vectơ r1, r2 . Giả sử m1 = m2 và r1 = - r2 . Thấy rằng Q1.r1 = Q2.r2 , vật ở trạng thái cân bằng tĩnh. Trọng tâm tổng của vật nằm trên trục quay. Khi trục quay với vận tốc góc w, sẽ xuất hiện những lực quán tính li tâm: 2 Pi m i. r i .w ; i 1,2 Thấy rằng ở trạng thái động dù P1 = - P2 nhƣng do nằm trên 2 mặt phẳng cách nhau một khoảng L nên chúng không triệt tiêu nhau, mà tạo thành một ngẫu lực M=P2.L, ngẫu lực này sẽ gây nên các phản lực tại các ổ => gây ra mất cân bằng. Chương 4 CÂN BẰNG MÁY 4.3. Cân bằng động vật quay dày 4.3.1. Lý do phải cân bằng động Nhƣ vậy tuy vật cân bằng ở trạng thái tĩnh nhƣng ở trạng thái động khi vật quay quanh trục, ngẫu lực sinh ra sẽ làm vật mất cân bằng. Lý do phải thực hiện cân bằng động. Vậy, để cân bằng vật quay dày, hai điều kiện sau cần phải đƣợc thỏa mãn: qt Pi 0 qt Mi 0 Chương 4 CÂN BẰNG MÁY 4.3. Cân bằng động vật quay dày 4.3.2. Vật quay dày Vật quay dày . Vật quay dày đƣợc định nghĩa là “vật quay mà các khối lượng của nó được coi như phân bố trên nhiều mặt phẳng khác nhau vuông góc với trục quay”. . Ví dụ về vật quay dày: rôto của máy điện, trục khuỷu, Chương 4 CÂN BẰNG MÁY 4.3. Cân bằng động vật quay dày 4.3.3. Nguyên tắc cân bằng vật quay dày Phƣơng pháp chia lực Chương 4 CÂN BẰNG MÁY 4.3. Cân bằng động vật quay dày 4.3.3. Nguyên tắc cân bằng vật quay dày Phƣơng pháp chia lực . Thay thế một lực bằng hai lực song song có cùng tác dụng về lực và momen Thanh AB có lực P đặt a b tại C Ta thay thế lực P bởi A C B hai lực P1 và P2 hoàn toàn tƣơng đƣơng về P tác dụng lực và mômen 1 P2 nếu: P PPP i 12 P12.. a P b Chương 4 CÂN BẰNG MÁY 4.3. Cân bằng động vật quay dày 4.3.3. Nguyên tắc cân bằng vật quay dày Cân bằng vật quay dày . Giả sử có vật quay dày với các khối lƣợng m1, m2, m3 tập trung trên 3 mặt phẳng 1, 2 và 3 vuông góc với trục quay của vật, vị trí của chúng đƣợc xác định bởi các bán kính véctơ . . Khi cho đĩa quay với vận tốc góc ω sẽ xuất hiện các lực quán tính li tâm: 2 Pii m1. r .w ; i 1,2,3 . Để cân bằng ta sẽ dùng phƣơng pháp chia lực: Chọn hai mặt phẳng I, II tùy ý vuông góc với trục quay làm những mặt phẳng cân bằng. Khoảng các từ các mặt phẳng 1, 2, 3 đến hai mặt phẳng I, II lần lƣợt là a1, a2, a3 và b1, b2, b3. Trong mặt phẳng chứa lực và trục quay ta chia thành hai lực thành phần nằm trên hai mặt phẳng cân bằng I, II. Phép chia phải thỏa mãn điều kiện sau: I II PPPi i i I II i i i i P.. a P b Chương 4 CÂN BẰNG MÁY 4.3. Cân bằng động vật quay dày 4.3.2. Nguyên tắc cân bằng vật quay dày a3 b3 a2 b2 a1 b1 1 P2 2 3 I Pcb I m II mcb 2 Pcb I PII P r2 2 m II 2 cb I P3 w r r3 PII I 1 m 3 P1 3 PII 1 m 1 P 3 II I P1 II Pcb I Pcb P I II 2 P2 P I II I 3 P3 P1 II P1 Chương 4 CÂN BẰNG MÁY 4.3. Cân bằng động vật quay dày 4.3.2. Nguyên tắc cân bằng vật quay dày Cân bằng vật quay dày . Ta thấy các lực quán tính li tâm trong các mặt phẳng 1, 2, 3 đã đƣợc chia về hai mặt phẳng cân bằng I, II và hai hệ lực phẳng mới hoàn toàn tƣơng đƣơng với hệ lực không gian ban đầu về cả phƣơng diện lực và mômen. . Muốn vật cân bằng thì tổng các lực trên từng mặt phẳng cân bằng I, II phải bằng không. Do đó ta tiến hành cân bằng trên từng mặt I II phẳng bằng cách đặt lên chúng các khối lƣợng mcb , mcb sao cho khi vật quay, các lực quán tính li tâm: I I I22 II II II Pcb m cb..,.. r cbww P cb m cb r cb thỏa mãn: IIII PPPP1 2 3 cb 0 II II II II PPPP1 2 3 cb 0 Chương 4 CÂN BẰNG MÁY 4.3. Cân bằng động vật quay dày 4.3.2. Nguyên tắc cân bằng vật quay dày Cân bằng vật quay dày I II . Bằng phƣơng pháp đa giác lực ta xác định đƣợc Pcb và Pcb từ đó xác định đƣợc cần đặt lên hai mặt phẳng cân bằng những khối lƣợng bằng bao nhiêu và ở vị trí nào để vật cân bằng. . Nhận xét: • Để cân bằng vật quay dày ta sẽ cần ít nhất 2 đối trọng đặt trên 2 mặt phẳng khác nhau vuông góc với trục quay. • Trong thực tế cần tiến hành trên máy cân bằng động. Chương 4 CÂN BẰNG MÁY 4.3. Cân bằng động vật quay dày 4.3.3. Giới thiệu về máy cân bằng động Chương 4 CÂN BẰNG MÁY 4.3. Cân bằng động vật quay dày 4.3.3. Giới thiệu về máy cân bằng động Chương 4 CÂN BẰNG MÁY 4.3. Cân bằng động vật quay dày 4.3.3. Giới thiệu về máy cân bằng động |Pb| Chương 4 CÂN BẰNG MÁY 4.3. Cân bằng động vật quay dày 4.3.3. Giới thiệu về máy cân bằng động Chương 4 CÂN BẰNG MÁY 4.3. Cân bằng động vật quay dày 4.3.3. Giới thiệu về máy cân bằng động Chương 4 CÂN BẰNG MÁY 4.3. Cân bằng động vật quay dày 4.3.3. Giới thiệu về máy cân bằng động Cân bằng trục ngang Cân bằng trục dọc Chương 4 CÂN BẰNG MÁY 4.3. Cân bằng động vật quay dày 4.3.3. Giới thiệu về máy cân bằng động Chương 4 CÂN BẰNG MÁY 4.4. Cân bằng cơ cấu . Chỉ xét trƣờng hợp cơ cấu phẳng. . Bất kỳ cơ cấu nào cũng là một hệ chất điểm có khối tâm luôn di động trong quá trình chuyển động của cơ cấu. Khi thu gọn các lực quán tính trong cơ cấu về khối tâm sẽ thu đƣợc một véctơ chính Pqt và mômen chính Mqt . Cơ cấu sẽ cân bằng nếu trong quá trình chuyển động của nó Pqt và Mqt luôn bằng không. Do việc cân bằng mômen chính rất phức tạp nên ta sẽ tập trung vào việc cân bằng lực quán tính chính với: Pqt Ma S Trong đó: m là khối lƣợng cả cơ cấu aS là gia tốc của khối tâm S của cơ cấu Chương 4 CÂN BẰNG MÁY 4.4. Cân bằng cơ cấu . Muốn triệt tiêu lực P thì gia tốc aS của khối tâm phải bằng không khối tâm phải cố định hoặc chuyển động thẳng đều. . Trƣờng hợp cơ cấu chuyển động thẳng đều ít xảy ra do cơ cấu thông thƣờng chuyển động có chu kỳ, nên bài toán cân bằng cơ cấu nhiều khâu qui về việc phân bố khối lƣợng của các khâu sao cho khối tâm chung của cơ cấu phải cố định. n m .r i Si n i 1 rS const với m mi m i 1 rS là bán kính véc tơ khối tâm chung của cơ cấu. ri là bán kính véc tơ khối tâm của khâu thứ i có khối lƣợng mi. Chương 4 CÂN BẰNG MÁY 4.4. Cân bằng cơ cấu Xét cơ cấu tay quay con trƣợt B S1 S2 r1 r 2 S C S3 A rs r3 . Khối tâm chung của cơ cấu đƣợc xác định bởi véctơ r : S m1... r 1 m 2 r 2 m 3 r 3 r với r1 s 1;; r 2 l 1 s 2 r 3 l 1 l 2 s 3 s m m1. s 1 m 2 .( l 1 s 2 ) m 3 .( l 1 l 2 s 3 ) rs m ms. ( m mlms ). . ml . ms . r 11 2 31 22 32 33 s m Chương 4 CÂN BẰNG MÁY 4.4. Cân bằng cơ cấu Xét cơ cấu tay quay con trƣợt B S1 S2 r1 r 2 S C S3 A rs r3 Muốn rS không đổi, điều kiện sau buộc phải thỏa mãn: ()mm 23 sl11 . m1. s 1 ( m 2 m 3 ). l 1 0 m 1 m. s m . l 0 m 2 2 3 2 sl 3 . 22 m2 Đây là những điều kiện của trọng tâm khâu (1) và (2) để khối tâm chung S của cơ cấu tay quay con trƣợt có vị trí không đổi, khi đó cơ cấucânđƣợcsẽbằng. Chương 4 CÂN BẰNG MÁY 4.4. Cân bằng cơ cấu Xét cơ cấu tay quay con trƣợt Sau khi phân bố lại khối lƣợng trên các khâu Trọng tâm của cơ cấu cố định tại S ( không thay đổi tại mọi vị trí của cơ cấu) trong quá trình làm việc Vậy: cân bằng cơ cấu là phân bố lại khối lượng sao cho trọng tâm S cố định.
File đính kèm:
 bai_giang_nguyen_ly_may_chuong_4_can_bang_may_nguyen_chi_hun.pdf
bai_giang_nguyen_ly_may_chuong_4_can_bang_may_nguyen_chi_hun.pdf

