Bài giảng Lập và phân tích dự án cho kỹ sư - Chương 2: Giá trị theo thời gian của tiền tệ - Nguyễn Ngọc Bình Phương

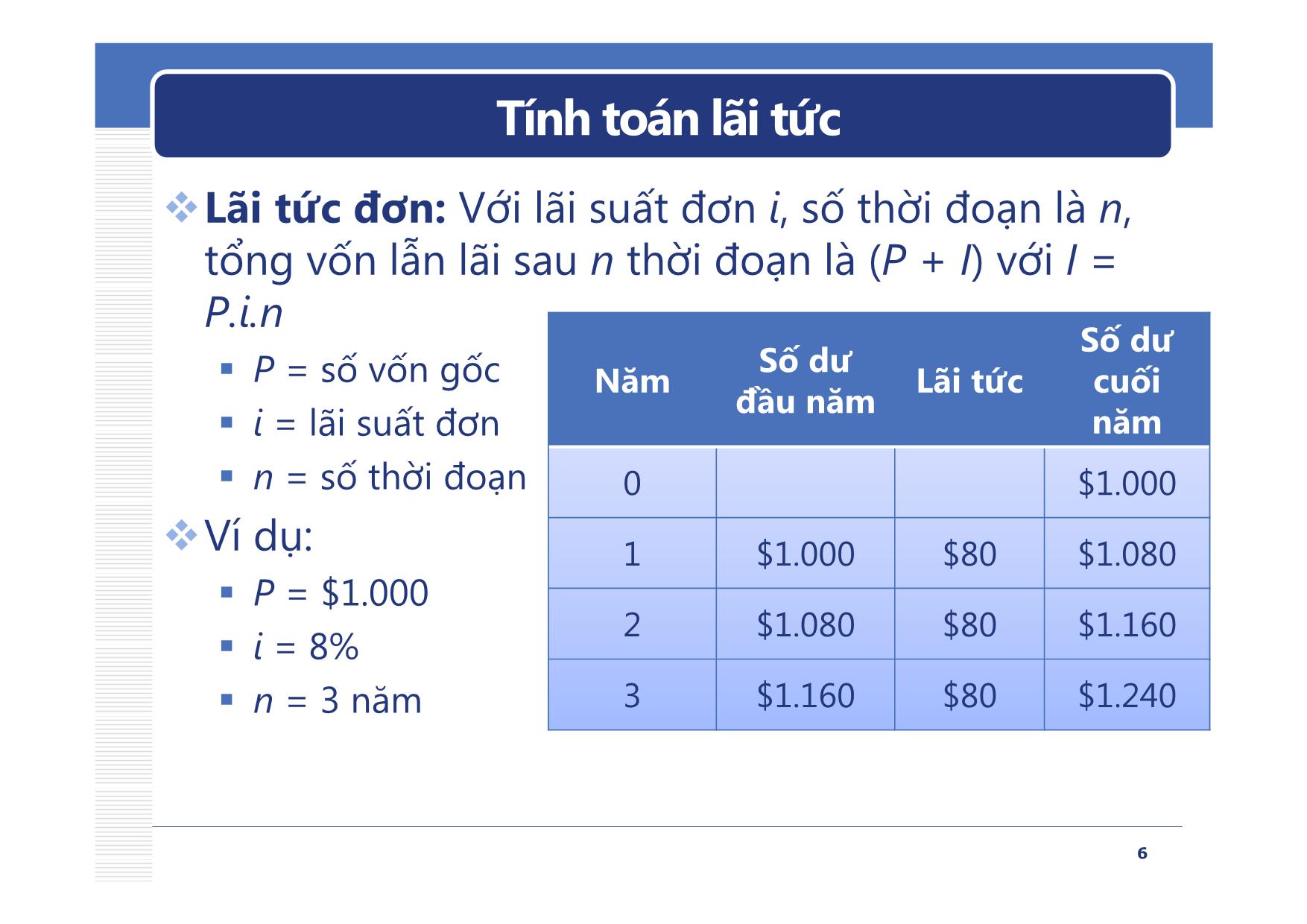
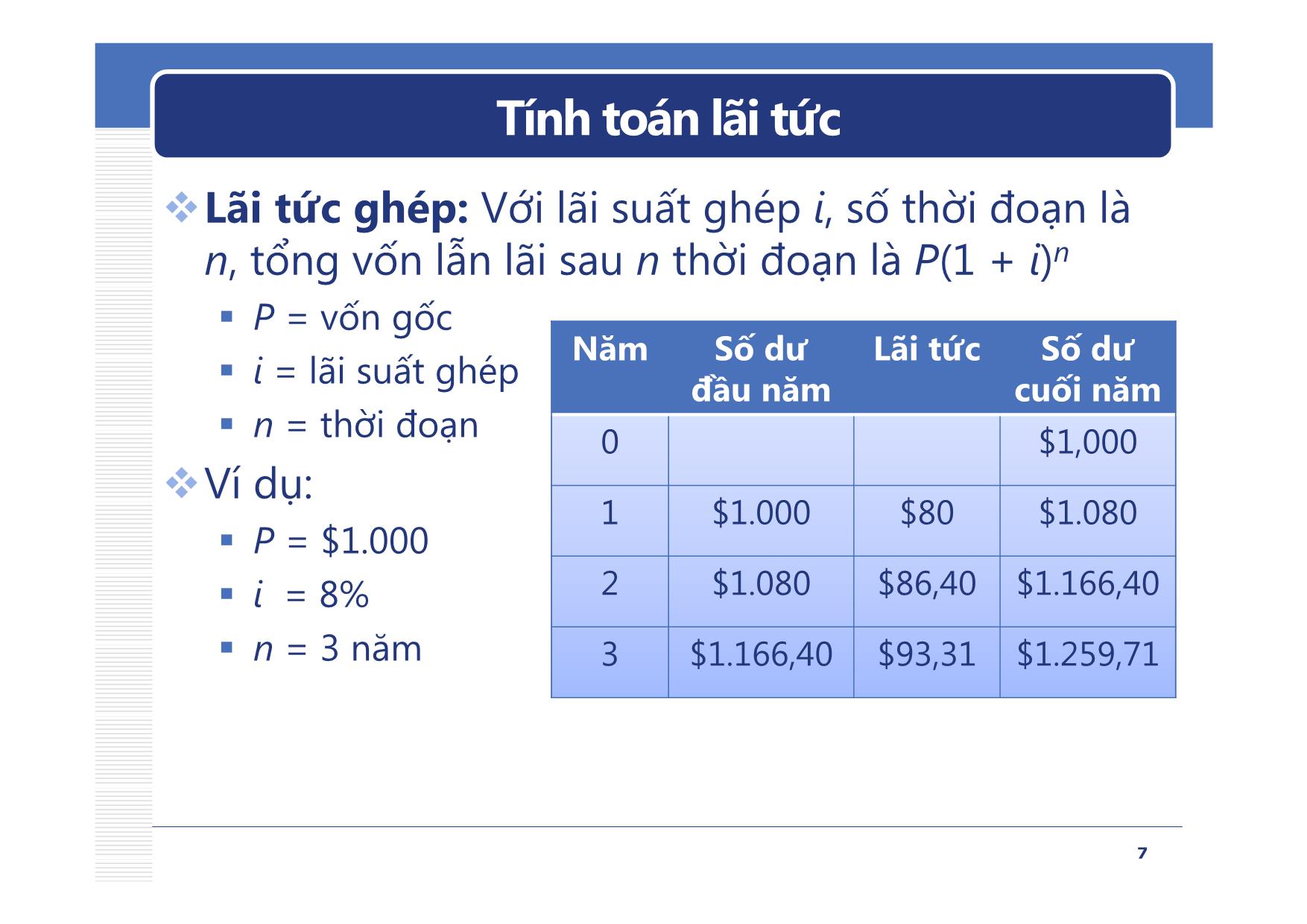
Chương 2
GIÁ TRỊ THEO THỜI GIAN CỦA TIỀN TỆ
 Nguyễn Ngọc Bình Phương
 nnbphuong@hcmut.edu.vn
 Khoa Quản lý Công nghiệp
 Đại học Bách Khoa – TP.HCM
 Nội dung
 1. Tính toán lãi tức
 2. Biểu đồ dòng tiền tệ (CFD)
 3. Các công thức tính giá trị tương đương cho
 các dòng tiền tệ đơn và phân bố đều
 4. Lãi suất danh nghĩa và lãi suất thực
Không học: Các công thứctínhgiátrị tương đương cho các dòng tiềntệ
phân bố không đều&Cáccôngthứctínhgiátrị tương đương khi ghép
lãi liên tục
 2
 Tính toán lãi tức
™Lãi tức (interest) là biểu hiện giá trị theo thời gian 
 của tiền tệ. 
 Lãi tức = (Tổng vốn tích luỹ) – (Vốn đầu tư ban đầu)
™Lãi suất (interest rate) là lãi tức biểu thị theo tỷ lệ 
 phần trăm đối với số vốn ban đầu cho một đơn vị 
 thời gian:
Lãi suất = (Lãi tức trong 1 đơn vị thời gian) / (Vốn gốc) x 100%
 3
 Tính toán lãi tức
™Sự tương đương về mặt kinh tế (economic 
 equivalence)
 ƒ Những số tiền khác nhau ở những thời điểm 
 khác nhau có thể bằng nhau về giá trị kinh tế.
 ƒ Với lãi suất 10%/năm, 1 triệu hôm nay tương 
 đương 1,1 triệu năm sau.
 ƒ Nếu gửi tiết kiệm P đồng hôm nay F - future
 trong n thời đoạn với lãi suất i
 thì sẽ có F (> P) đồng 0
 cuối thời đoạn n. n
 P - present
 4
 Tính toán lãi tức
™Lãi tức đơn (simple interest)
 ƒ Lãi tức chỉ tính theo số vốn gốc mà không tính 
 thêm lãi tức tích luỹ phát sinh từ tiền lãi ở các 
 thời đoạn trước đó.
™Lãi tức ghép (compound interest)
 ƒ Lãi tức ở mỗi thời đoạn được tính theo số vốn 
 gốc và cả tổng số tiền lãi tích luỹ được trong 
 các thời đoạn trước đó.
 ƒ Phản ánh được hiệu quả giá trị theo thời gian 
 của đồng tiền cho cả phần tiền lãi trước đó.
 ƒ Thường được sử dụng trong thực tế.
 5
 Tính toán lãi tức
™Lãi tức đơn: Với lãi suất đơn i, số thời đoạn là n, 
 tổng vốn lẫn lãi sau n thời đoạn là (P + I) với I = 
 P.i.n
 Số dư
 Số dư
 ƒ P = số vốn gốc Năm Lãi tức cuối
 đầunăm
 ƒ i = lãi suất đơn năm
 ƒ n = số thời đoạn 0 $1.000
™Ví dụ: 1 $1.000 $80 $1.080
 ƒ P = $1.000
 2 $1.080 $80 $1.160
 ƒ i = 8%
 ƒ n = 3 năm 3 $1.160 $80 $1.240
 6
 Tính toán lãi tức
™Lãi tức ghép: Với lãi suất ghép i, số thời đoạn là 
 n, tổng vốn lẫn lãi sau n thời đoạn là P(1 + i)n
 ƒ P = vốn gốc
 NămSố dư Lãi tứcSố dư
 ƒ
 i = lãi suất ghép đầunăm cuốinăm
 ƒ n = thời đoạn 0 $1,000
™Ví dụ:
 1 $1.000 $80 $1.080
 ƒ P = $1.000
 ƒ i = 8% 2 $1.080 $86,40 $1.166,40
 ƒ n = 3 năm 3 $1.166,40 $93,31 $1.259,71
 7
 Biểu đồ dòng tiềntệ (CFD)
™Dòng tiền tệ (Cash Flow - CF):
 ƒ CF bao gồm các khoản thu và các khoản chi, 
 được quy về cuối thời đoạn. 
 ƒ Trong đó, khoản thu được quy ước là CF 
 dương ( ), khoản chi là CF âm ( )
 ƒ Dòng tiền tệ ròng = Khoản thu – Khoản chi 
™Biểu đồ dòng tiền tệ (Cash Flow Diagrams -
 CFD): là một đồ thị biểu diễn các dòng tiền tệ 
 theo thời gian.
 8
 Biểu đồ dòng tiền tệ (CFD)
Các ký hiệu dùng trong CFD:
™P (present): Giá trị hay tổng số tiền ở mốc thời 
 gian quy ước nào đó được gọi là hiện tại. Trên 
 CFD, P ở cuối thời đoạn 0.
™F (future): Giá trị hay tổng số tiền ở mốc thời 
 gian quy ước nào đó được gọi là tương lai. Trên 
 CFD, F có thể ở cuối bất kỳ thời đoạn thứ N nào.
™A (annuity): Một chuỗi các giá trị tiền tệ có giá 
 trị bằng nhau đặt ở cuối các thời đoạn
™n: Số thời đoạn (năm, tháng,)
™i (interest rate): Lãi suất (mặc định là lãi suất 
 ghép)
 9
 Các công thức tính giá trị tương đương cho dòng tiền 
 đơn và phân bố đều
™Công thức tính giá trị tương đương cho dòng 
 tiền tệ đơn:
 FP=+(1 i ) n
 FPFPin= (/,,)
™Công thức tính giá trị tương đương cho dòng 
 tiền tệ phân phối đều:
 (1+−i )n 1
 FA=
 i
 = AF(/,,) Ain
 10
Các công thức tính giá trị tương đương cho dòng tiền 
 đơn và phân bố đều
Tìm BiếtCôngthứcKýhiệu
 FP (1+ i ) n (F / P, i, n)
 1
 PF (1+ i ) n (P / F, i, n)
 (1+−i )n 1
 PA ii(1+ ) n (P / A, i, n)
 + n
 AP ii(1 ) (A / P, i, n)
 (1+−i )n 1
 n
 FA (1+−i ) 1 (F / A, i, n)
 i
 AF i (A / F, i, n)
 (1+−i )n 1
 11
Các công thức tính giá trị tương đương cho dòng tiền 
 đơn và phân bố đều
 (F / P, 5%, 10) = 1,629
 12
 Các công thức tính giá trị tương đương cho dòng tiền 
 đơn và phân bố đều
Hàm Excel
™FV(rate, nper, pmt, pv, type)
™PV(rate, nper, pmt, fv, type)
™PMT(rate, nper, pv, fv, type)
Trong đó
™ rate: Lãi suất
™ nper: số thời đoạn
™ pv: giá trị hiện tại P [=0 nếu để trống]
™ fv: giá trị tương đương F [=0 nếu để trống]
™ pmt: giá trị trả đều A [=0 nếu để trống]
™ type = 0 (mặc định, thanh toán cuối kỳ)
 13
 Các công thức tính giá trị tương đương cho dòng tiền 
 đơn và phân bố đều
™Ví dụ 1: Nếu bạn đầu tư $2.000 bây giờ với lãi 
 suất 10%/nămthì8 năm sau bạn sẽ có bao 
 nhiêu? 
 F = ?
 i = 10%
 0
 8
 P = $2.000
 F = P(F/P,i,n) = 2.000(F/P,10%,8)=2.000*2,144=4.287,2
 FV(rate,nper,pmt,pv,type) = FV(10%,8,,-2000)=$4,287.18 
 14
 Các công thức tính giá trị tương đương cho dòng tiền 
 đơn và phân bố đều
™Ví dụ 2: Bạn muốn để dành một khoản tiền hôm 
 nay với lãi suất 7%/năm để có $10.000 trong 6 
 năm. Vậy bạn cần để dành bao nhiêu ngay hôm 
 nay?
 F = $10.000
 i = 7 %
 0
 6
 P = ?
 P = F(P/F,i,n) = 10.000 (P/F,7%,6)=10.000*0,666=6660
 PV(rate,nper,pmt,fv,type) = PV(7%,6,,10000)=($6,663.42) 
 15
 Các công thức tính giá trị tương đương cho dòng tiền 
 đơn và phân bố đều
™Ví dụ 3: Bạn sẽ phải gửi tiết kiệm bao nhiêu ngay 
 hôm nay để có thể rút $25.000 vào năm thứ 1, 
 $3.000 vào năm thứ 2, $5.000 vào năm thứ 4, với 
 lãi suất là 10%/năm? $25.000
 $3.000 $5.000
 0
 1 2 3 4
 P = ?
 P = F1(P/F,i,1) + F2(P/F,i,2) + F4(P/F,i,4)
 =25*0,909+3*0,826+5*0,683=28,618 
 16
 Các công thức tính giá trị tương đương cho dòng tiền 
 đơn và phân bố đều
™Ví dụ 4: Nếu hàng năm bạn gửi $5.000 tiết kiệm 
 với lãi suất 6%/năm trong 5 năm thì cuối năm thứ 
 5 bạn nhận được bao nhiêu?
 F =?
 i = 6%
 0 1 2 3 4 5
 $5.000 $5.000 $5.000 $5.000 $5.000
 F = A(F/A,i,n) = 5.000(F/A,6%,5)=5.000*5,637 =28.185,45 
 FV(rate,nper,pmt,pv,type) = FV(6%,5,-5000)=$28,185.46 
 17
 Các công thức tính giá trị tương đương cho dòng tiền 
 đơn và phân bố đều
™Ví dụ 5: Để hàng năm có thể nhận được $7,92 
 triệu trong vòng 25 năm, bạn phải gửi tiết kiệm 
 ngay hôm nay khoản tiền là bao nhiêu, biết lãi 
 suất là 8%/năm? A = $7,92
 0
 12 25
 i = 8%
 P = ?
 P = A(P/A,i,n)=7,92(P/A,8%,25)=7,92*10,675 = 84,546 
 PV(rate,nper,pmt,fv,type) = PV(8%,25,7.92)=($84.54) 
 18
 Lãi suất thực và lãi suất danh nghĩa
™ Thông thường, giá trị lãi suất được dùng để tính tiền lãi 
 trong thời đoạn 1 năm hay còn gọi thời đoạn phát biểu 
 lãi là 1 năm. Trong thực tế, thời đoạn phát biểu lãi có thể 
 ít hơn 1 năm.
™ Xét ví dụ:Lãi suất 12%/năm, ghép lãi theo quý, 6 tháng 
 lãnh lãi một lần
 ƒ Thời đoạn phát biểu lãi: 1 năm
 ƒ Thời đoạn ghép lãi: 1 quý
 ƒ Thời đoạn trả lãi (thời đoạn tính toán): 6 tháng
z Khi thời đoạn phát biểu lãi phù hợp với thời đoạn ghép 
 lãi thì đó là lãi suất thực (effective interest rate). Nếu 
 thời đoạn phát biểu lãi khác thời đoạn ghép lãi thì đó là 
 lãi suất danh nghĩa (nominal interest rate).
 19
 Lãi suất thực và lãi suất danh nghĩa
™ Tính chuyển lãi suất danh nghĩa theo những thời 
 đoạn khác nhau:
 Gọi rngan là lãi suất danh nghĩa ở thời đoạn ngắn (Vd: tháng)
 rdai là lãi suất danh nghĩa ở thời đoạn dài (Vd: năm)
 m là số thời đoạn ngắn trong thời đoạn dài (Vd: m = 12)
™ Ví dụ: ࢊࢇ࢏ ࢔ࢍࢇ࢔
 ƒ Lãi suất 3%/quý ⇒ Mặc định hiểu là lãi suất thực theo quý: 
 3%/quý (ghép lãi theo quý)
 ƒ Lãi suất danh nghĩa 3%/quý ⇒ Lãi suất danh nghĩa theo năm là 
 3%*4 = 12%/năm
 ƒ Lãi suất 20%/năm, ghép lãi theo quý ⇒ Lãi suất danh nghĩa theo 
 năm, ghép lãi theo quý ⇒ Lãi suất danh nghĩa theo quý = Lãi suất 
 thực theo quý = 5%/quý
 20
 Lãi suất thực và lãi suất danh nghĩa
 ™ Tính chuyển lãi suất thực theo những thời đoạn khác 
 nhau:
 Gọi ingan là lãi suất thực ở thời đoạn ngắn (Vd: tháng)
 idai là lãi suất thực ở thời đoạn dài (Vd: năm)
 m là số thời đoạn ngắn trong thời đoạn dài (Vd: m = 12)
 ࢓ ࢓
 ࢊࢇ࢏ ࢔ࢍࢇ࢔ ࢔ࢍࢇ࢔ ࢊࢇ࢏
 ™ Tính chuyển lãi suất danh nghĩa sang lãi suất thực:
 ƒ Bước 1: Từ lãi suất danh nghĩa tính chuyển sang lãi suất 
 thực trong thời đoạn ghép lãi.
 ƒ Bước 2: Tính chuyển lãi suất thực trong thời đoạn ghép lãi 
 sang lãi suất thực trong thời đoạn tính toán.
 21
HẾT CHƯƠNG 2