Bài giảng Kỹ thuật siêu cao tần - Chương 3: Ma trận tán xạ - Phan Hồng Phương
Chỉ quan tâm đến quan hệ vào ra mà không cần quan
tâm đến cấu trúc bên trong của mạng Người
ta đưa ra các khái niệm: Hàm truyền, ma trận đặc
tính (ma trận trở kháng [Z], ma trận dẫn nạp [Y], ma
trận H, ma trận ABCD,
Trang 1
Trang 2
Trang 3
Trang 4
Trang 5
Trang 6

Trang 7
Trang 8

Trang 9
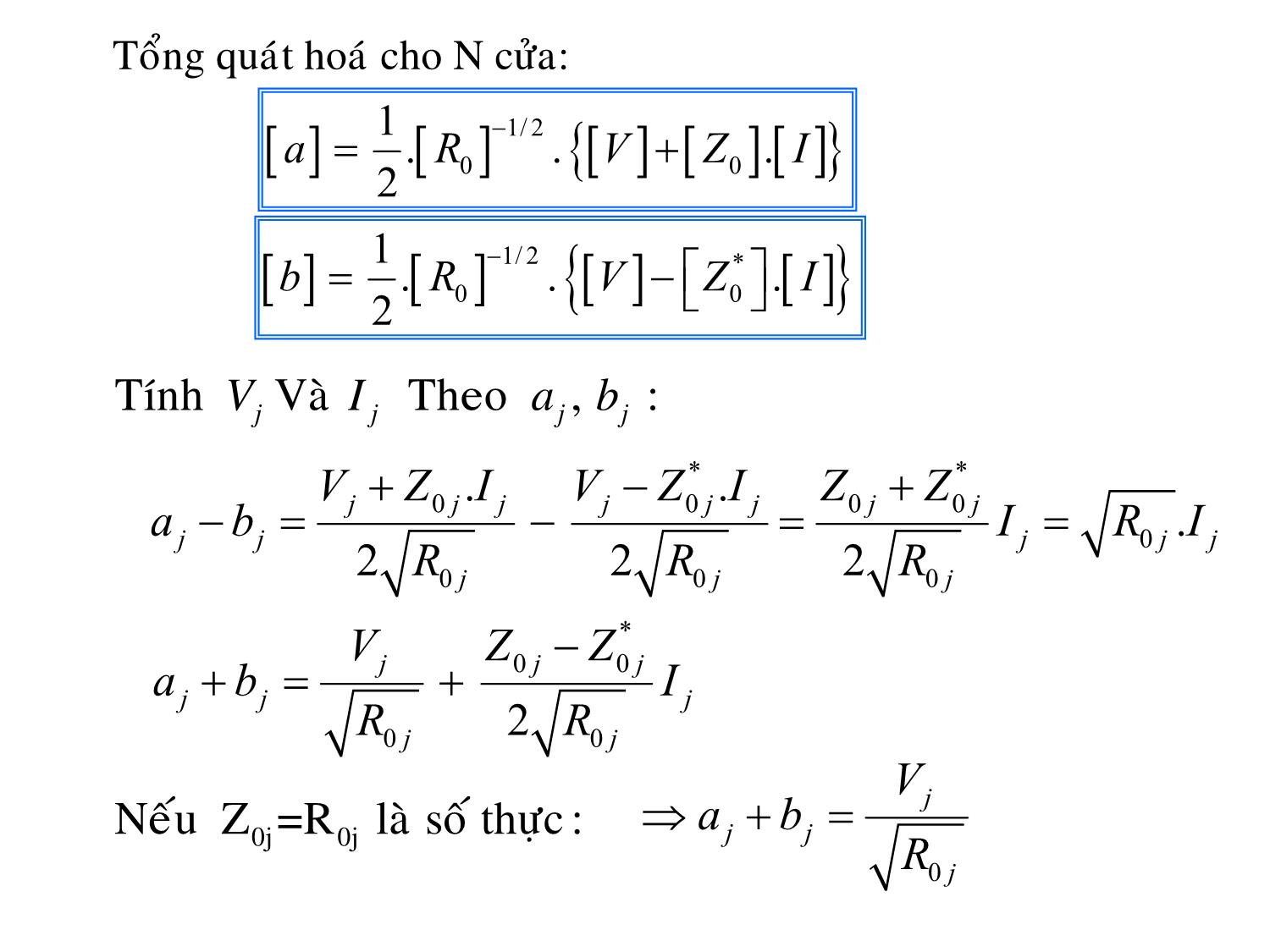
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Kỹ thuật siêu cao tần - Chương 3: Ma trận tán xạ - Phan Hồng Phương", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Kỹ thuật siêu cao tần - Chương 3: Ma trận tán xạ - Phan Hồng Phương
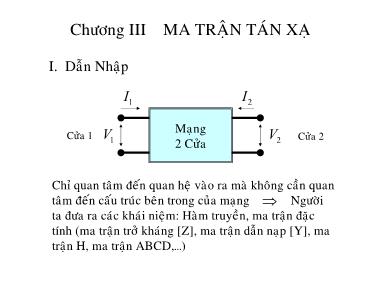
Chương III MA TRẬN TÁN XẠ
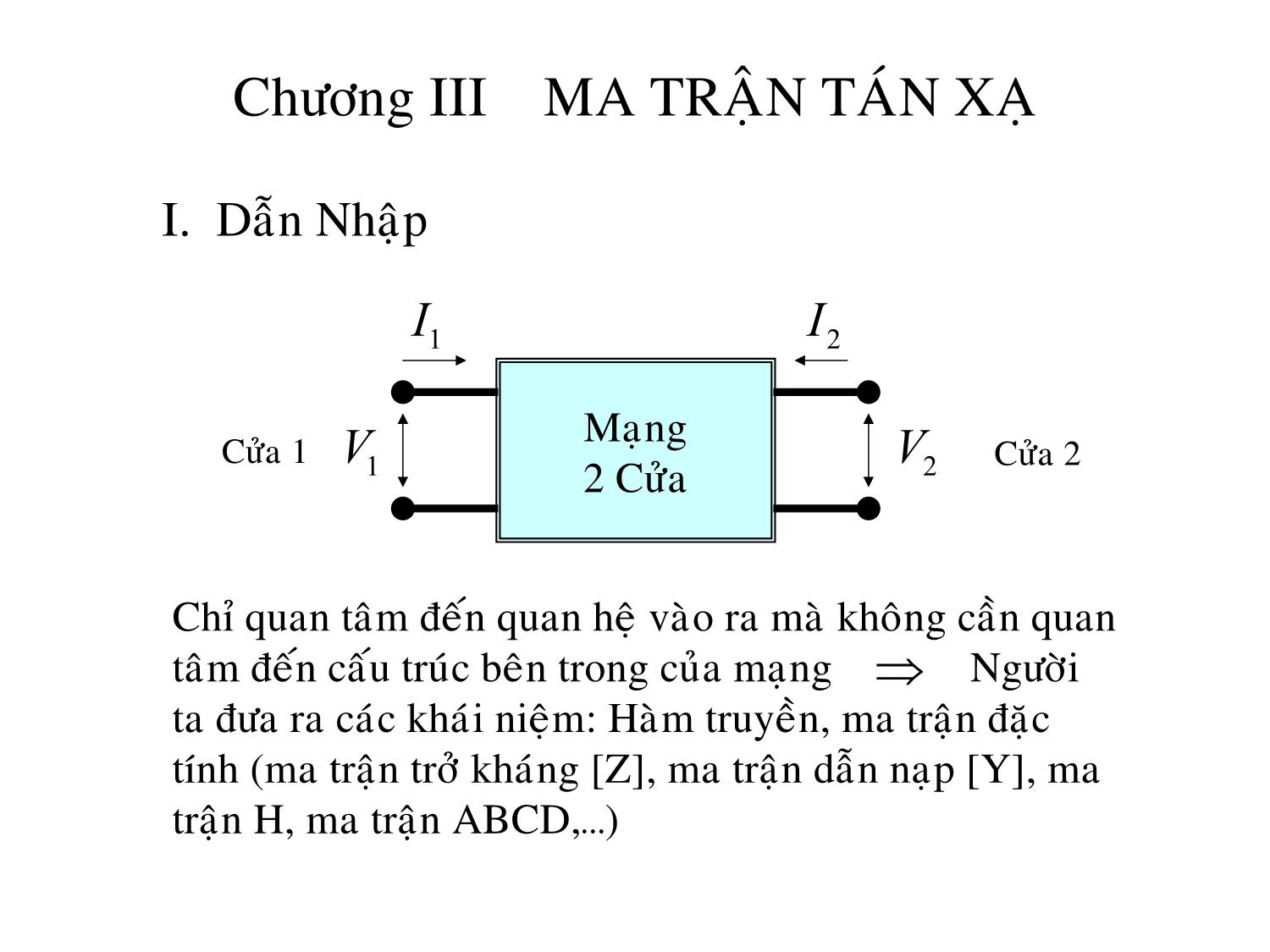
I. Dẫn Nhập
I1 I2
Mạng
Cửa 1 V V Cửa 2
1 2 Cửa 2
Chỉ quan tâm đến quan hệ vào ra mà không cần quan
tâm đến cấu trúc bên trong của mạng ⇒ Người
ta đưa ra các khái niệm: Hàm truyền, ma trận đặc
tính (ma trận trở kháng [Z], ma trận dẫn nạp [Y], ma
trận H, ma trận ABCD,)
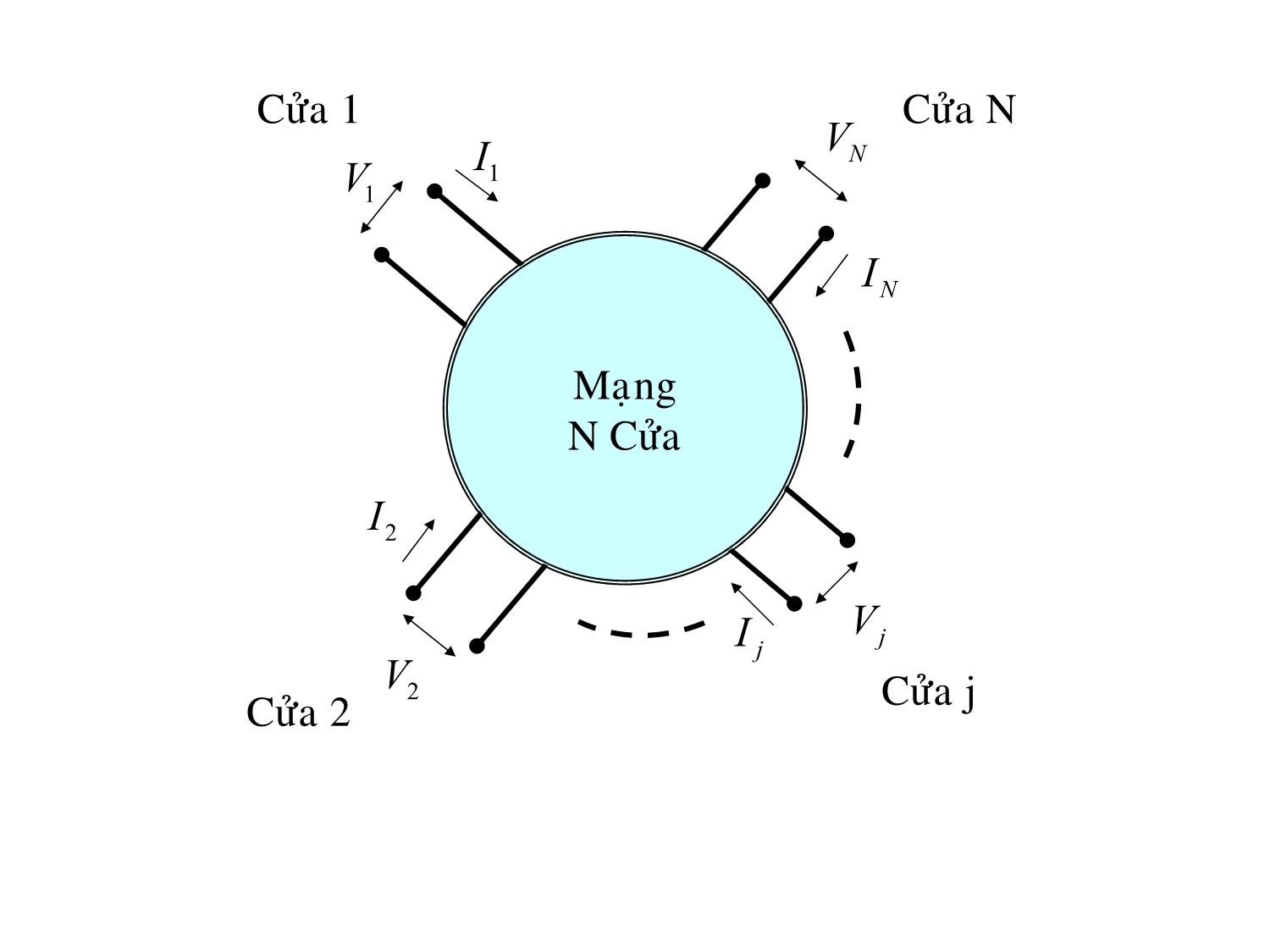
Cửa 1 Cửa N
VN
I1
V1
I N
Mạng
N Cửa
I2
V
I j j
V2 Cửa j
Cửa 2
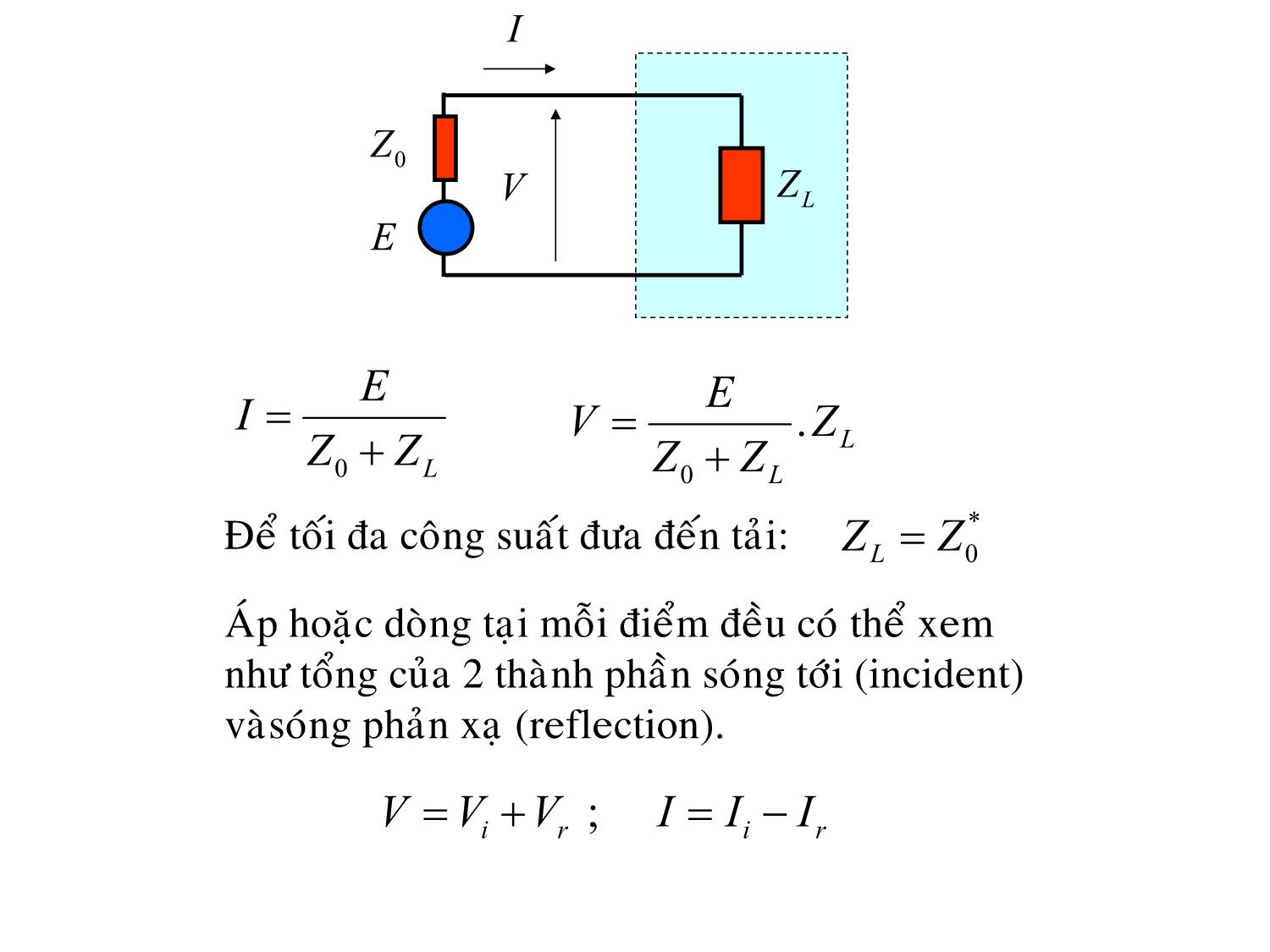
I
Z0
V ZL
E
E E
I = VZ= .
ZZ+ L
0 L ZZ0 + L
*
Để tối đa công suất đưa đến tải: ZZL = 0
Áp hoặc dòng tại mỗi điểm đều có thể xem
như tổng của 2 thành phần sóng tới (incident)
vàsóng phản xạ (reflection).
VVV= ir+=−; II ir I
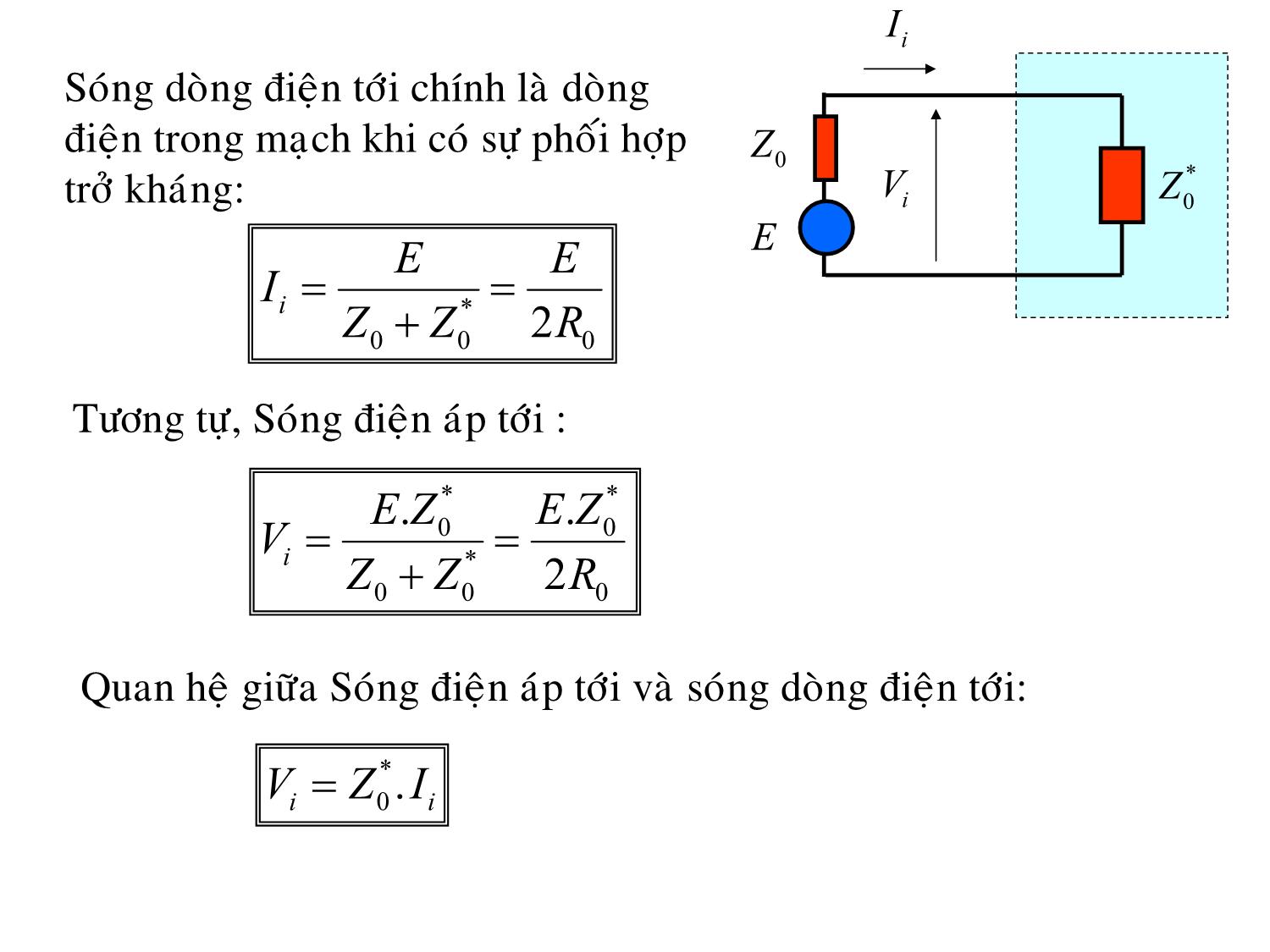
Ii
Sóng dòng điện tới chính là dòng
điện trong mạch khi có sự phối hợp
Z0
V Z *
trở kháng: i 0
E E E
Ii ==*
ZZ00+ 2 R 0
Tương tự, Sóng điện áp tới :
**
E..ZEZ00
Vi ==*
ZZ00+ 2 R 0
Quan hệ giữa Sóng điện áp tới và sóng dòng điện tới:
*
VZIii= 0 .
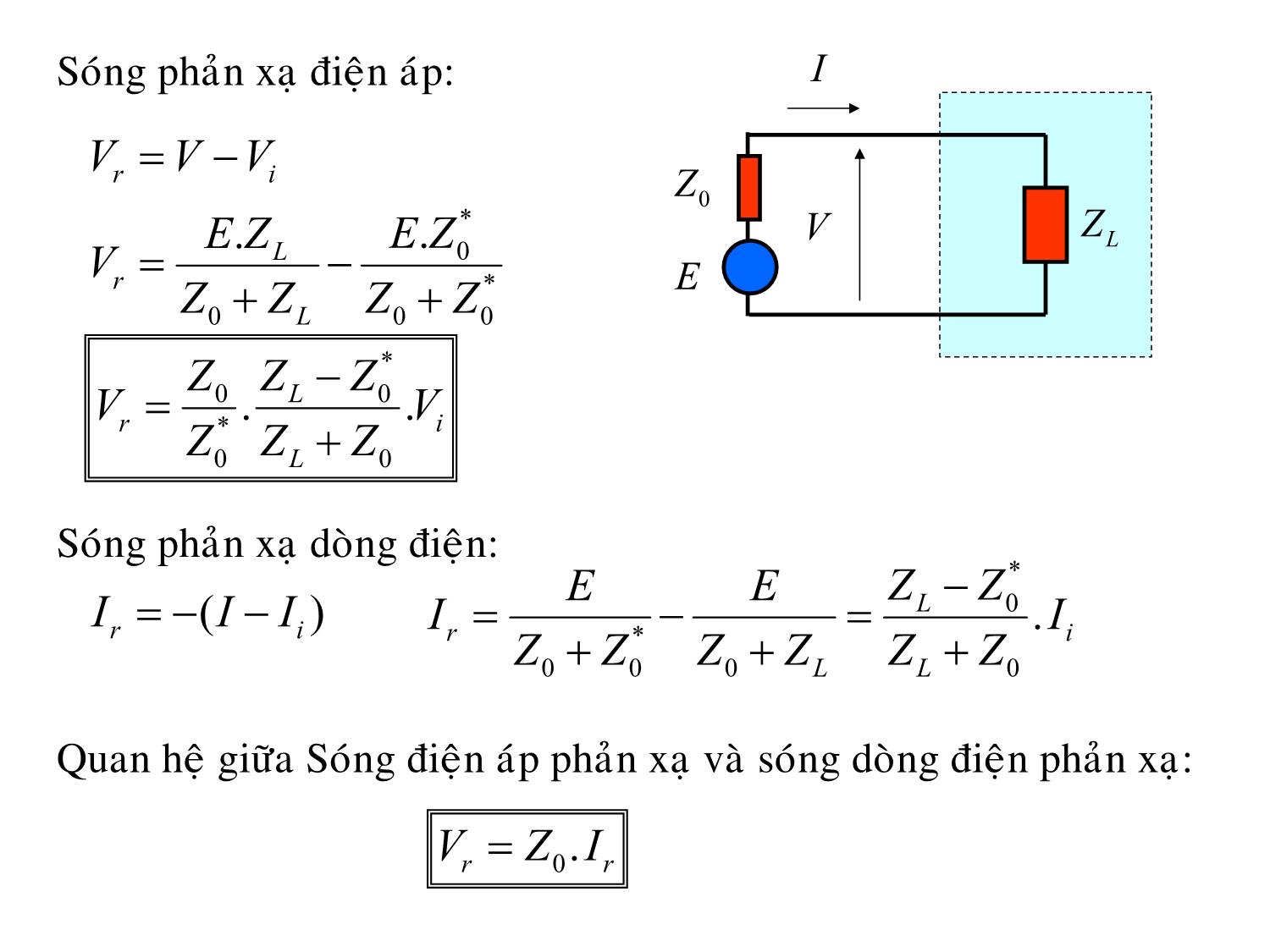
Sóng phản xạ điện áp: I
VVVri=−
Z0
* V Z
EZ. L E.Z0 L
Vr =−* E
ZZ000++L ZZ
*
ZZ00L − Z
VVri= * ..
ZZ00L + Z
Sóng phản xạ dòng điện:
EEZZ− *
I =−()II − L 0
riIri=−=* .I
ZZ00++ ZZ 0LL ZZ + 0
Quan hệ giữa Sóng điện áp phản xạ và sóng dòng điện phản xạ:
VZIrr= 0.
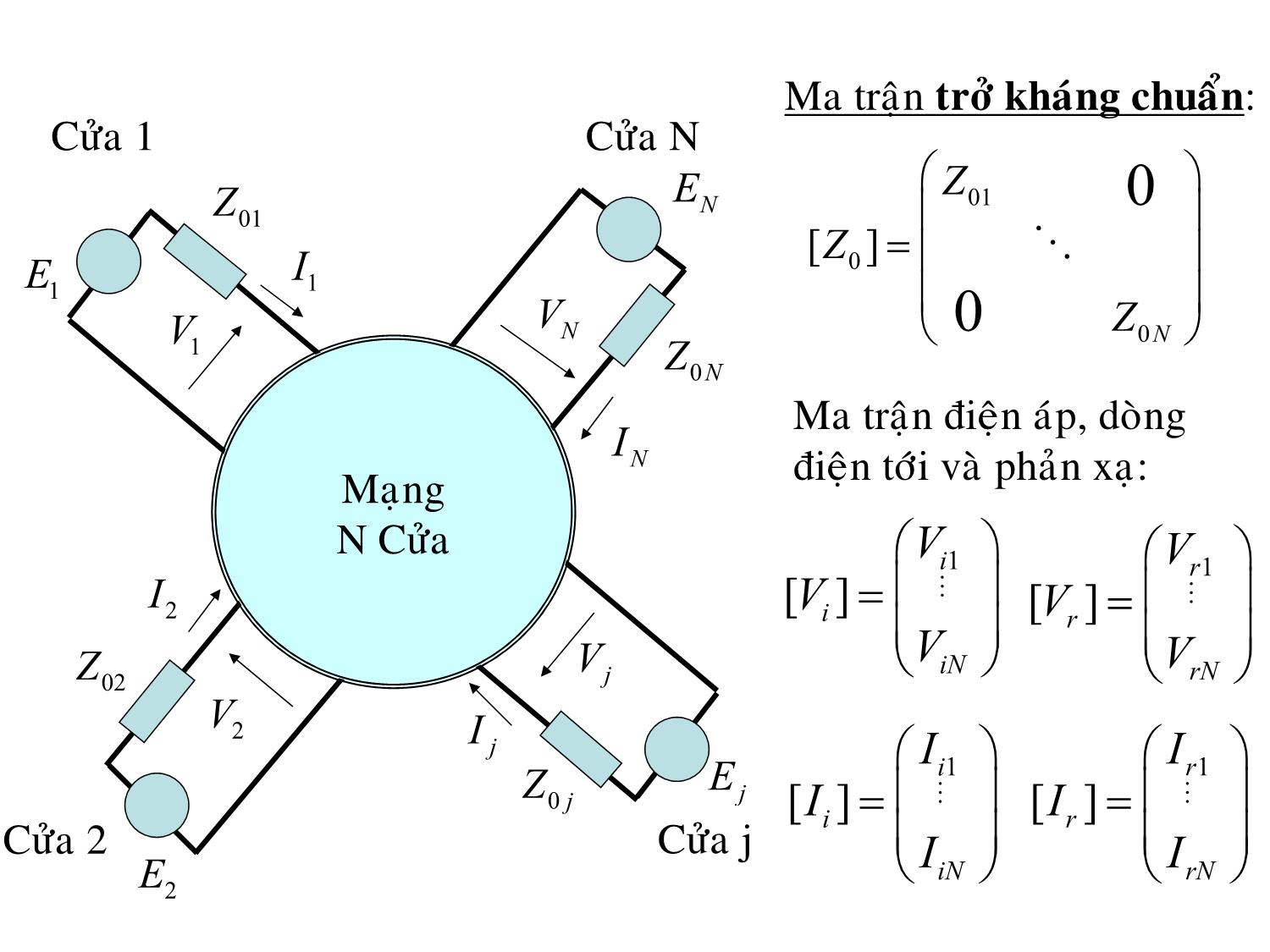
Ma trận trở kháng chuẩn:
Cửa 1 Cửa N
⎛⎞Z
EN 01 0
Z01 ⎜⎟
[]Z0 = ⎜⎟%
E I1
1 ⎜⎟
VN 0 Z0N
V1 ⎝⎠
Z0N
Ma trận điện áp, dòng
I
N điện tới và phản xạ:
Mạng
N Cửa V
⎛⎞i1 ⎛⎞Vr1
⎜⎟# #
I2 []Vi = []V = ⎜⎟
⎜⎟ r ⎜⎟
V ViN V
Z02 j ⎝⎠ ⎝⎠rN
V2 I
j ⎛⎞I ⎛⎞I
E i1 r1
Z0 j j ⎜⎟# ⎜⎟#
[]Ii = []Ir =
Cửa 2 Cửa j ⎜⎟ ⎜⎟
⎝⎠IiN ⎝⎠IrN
E2
Ma trận Tán Xạ của mạng N cửa: [S]
[b] = []S .[a]
⎡b1 ⎤ ⎛⎞SS11 12 " S1N ⎡a1 ⎤
⎜⎟
⎢⎥# = SS" S.⎢# ⎥
⎢⎥ ⎜⎟21 22 2N ⎢ ⎥
⎢ ⎥ ⎜⎟⎢ ⎥
⎣⎦bN ⎝ SSNN1 2 " S NN⎠ ⎣aN ⎦
Ma trận tán xạ thể hiện quan hệ giữa Sóng Tới [a]
và Sóng Về [b] tại các cửa.
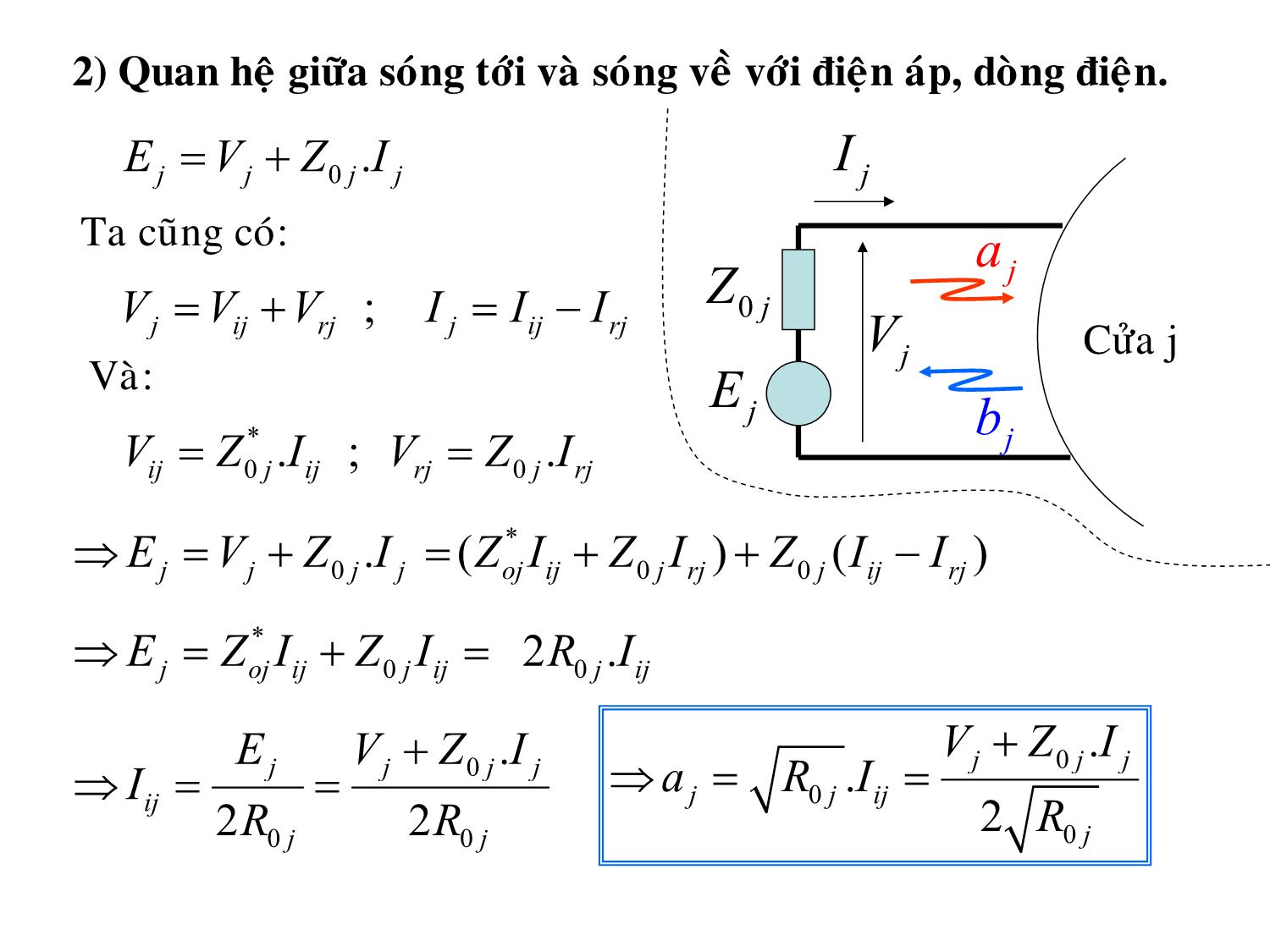
2) Quan hệ giữa sóng tới và sóng về với điện áp, dòng điện.
EVZIjj=+0 jj. I j
Ta cũng có:
a j
Z0 j
VVVj =+ij rjj; I =− IIij rj
Vj Cửa j
Và:
E j
* bj
VZIVZIij==00 j.; ij rj j . rj
*
⇒=+EVZIjj00 jj.( = ZIZIZIIoj ijj +rjj ) +0 (ij −rj )
*
⇒=EZIZIj oj ijj +00ijj =2. RIij
EVZI+ . VZIjjj+ 0 .
jjjj0 ⇒=aRI. =
⇒=Iij = jjij0
22RR00jj 2 R0 j
Quan hệ của sóng về theo dòng, áp tại cửa j:
Ta cũng có:
VVVjijrjjijrj=+; I =− II
Và:
*
VZIVZIij==00 j.; ij rj j . rj
** *
⇒−VZIjjj00.( = ZIZIZIIoj ijj +rjj )( −0ij −rj )
**
⇒−VZIZIZIjjjj00.2 =rj +oj rjj = RI0.rj
VZI− * . VZI− * .
jjj0 ⇒=bRI. =jjj0
⇒=Irj jjrj0
2R0 j 2 R0 j
Tổng quát hoá cho N cửa:
1 −1/2
[]aR=+..[]00{} [][][] VZI .
2
1 −1/2 *
[]bR=−..[]00 [] VZI⎡⎤ . []
2 { ⎣⎦ }
TínhVIj Vàjjj Theo ab , :
**
VZIjjjjjjjj+−000.. VZI Z + Z0
abjj−= − = Ij = RI0 jj.
222RRR000jjj
*
VZZjjj00−
abjj+= + Ij
RR00jj2
Vj
Nếu Z0j =R 0j là số thực : ⇒+=abjj
R0 j
3) Quan hệ giữa công suất với sóng tới và sóng về.
I j
P P
R0 j ij j
Vj
E j
Prj Cửa j
1
Công suất truyền vào cửa j: P = ReVI . *
jj2 ()j
1 **
Pjj=+−Re Rab00()jj./ abjjj R
2 { ()}
1
P =−+−Re aa** ab() ab *** bb
jj2 {}jjjjjjj
1 22
⇒=P ab −
jjj2 { }
4) Ý Nghĩa Vật Lý Của Các Hệ Số Trong Ma trận [S]
I1
I2
R R
01 a a 02
V 1 Mạng Hai Cửa 2
1 [S] V2
b1 b2
E1 E2
VRIjjj+ 0 .
Sóng tới tại cửa j: aRIjjij==0 .
2 R0 j
VRI− .
Sóng Về tại cửa j: bRI==. jjj0
jjrj0 2 R
0 j
⎡⎤ba11⎛⎞SS11 12 ⎡⎤ ⎧bSaSa1111122=+..
= ⎜⎟. ⇔ ⎨
⎢⎥baSS ⎢⎥
⎣⎦2 ⎝⎠21 22 ⎣2 ⎦ ⎩bSaSa2211222=+..
b
S : 1
Ý nghĩa của 11 S11 =
a1
a2 =0
a2 = 0: Có nghĩa không có sóng vào của 2 , Tức là: Nguồn
E2 bị triệt tiêu và có phối hợp trở kháng ở cửa 2.
I
1 I2
R01
a1 Mạng Hai Cửa
V b2
1 V2 R02
b1 [S]
E1
S11
VRI1011+ .
a1 =
2 R b
01 1 VRI1011− .
⇒=S11 ⇒=S
a 11 VRI+ .
1 a =0 1011ER=0, Tải
VRI1011− . 2 202
b1 =
2 R01 I
1 I2
R01
a1 Mạng Hai Cửa
V b2
1 V2 R02
b1 [S]
E1
S11= Γ 1
V1
Đặt: Z11 = Là trở kháng ngo õvào trong trường hợp :
I1
ER20= 0, Tải 2
ZR11− 01
⇒=S11 = Γ1
ZR11+ 01
⎧bSaSa1111122=+..
⎨
⎩bSaSa2211222=+..
b
S : 2
Ý nghĩa của 21 S21 =
a1
a2 =0
I
1 I2
R01
a1 Mạng Hai Cửa
V b2
1 V2 R02
b1 [S]
E1
Hệ số S21 : thể hiện hệ số truyền đạt từ cửa 1 sang cửa 2
1 2
2
b2
2 b2 2
S21 ==2
1 2
a1 a
a2 =0 2 1
1 2 1 2
P = a P = b
i112 r 222
I
1 I2
R01
a1 Mạng Hai Cửa
V b2
1 V2 R02
b1 [S]
E1
2
Hệ số S21 : thể hiện hệ số truyền đạt công suất từ cửa 1
sang cửa 2 trong điều kiện cửa 2 phối hợp trở kháng.
⎧bSaSa1111122=+..
⎨
⎩bSaSa2211222=+..
b
Ý nghĩa của S : 2
22 S22 = =Γ2
a2
a1=0
a1 = 0: Có nghĩa không có sóng vào của 1 , Tức là: Nguồn
E1 bị triệt tiêu và có phối hợp trở kháng ở cửa 1.
I
1 I2
a R
b1 Mạng Hai Cửa 2 02
R01 V V
1 [S] 2
b2
E2
S22
⎧bSaSa1111122=+..
⎨
⎩bSaSa2211222=+..
b
S : 1
Ý nghĩa của 12 S12 =
a2
a1=0
I
1 I2
a R
b1 Mạng Hai Cửa 2 02
R01 V V
1 [S] 2
b2
E2
S
22
Hệ số S12 : thể hiện hệ số truyền đạt từ cửa 2 sang cửa 1
5) Đo Các Hệ Số Ma trận tán xạ [S]
Bộ Chỉ Thị
Sóng Đứng
R
0 a1 a
Phần tử cần đo 2 Z
b [S] b L
E R0 1 2
Γ
Γ1 2
⎧bSaSa1111122=+..
⎨
⎩bSaSa2211222=+..
a ⎧bSaS=+Γ..() b
Γ= 2 ⇒ 11111222
2 b ⎨
2 ⎩bSaS22112222=+Γ..() b
⎧bSaS11111222=+Γ..() b
⎨
⎩bSaS22112222=+Γ..() b
S ⎡ SSΓ ⎤
ba= . 21 baS=+21 12 2
21−ΓS 1111⎢ ⎥
1.22 2 ⎣ 1.− S22Γ 2 ⎦
bSS12112Γ2
Γ=11 =S 1 +
aS121.− 2Γ2
a) Dùng : Tải bằng điện trở chuẩn
ZL = R0 ⇒Γ2 =0
bS121S21Γ2
Γ=11a =SS1 + = 11
aS121.−Γ22
Γ=2 0
b) Dùng : Tải ngắn mạch ⇒Γ =−1
ZL = 0 2
bS121S12
Γ=11b =S 1 −
aS121+ 2
Γ=−2 1
c) Dùng : Tải hở mạch ⇒Γ =1
ZL =∞ 2
bS121S12
Γ=11c =S 1 +
aS121− 2
Γ=2 1
SS21 21 SS21 21
Γ=111a S (1) Γ=111b S − (2) Γ=111c S + (3)
1+ S22 1− S22
(2) ⇒=+−ΓSS21 21 (1 S22 )( S 11 1b ) (4)
Thay (4), (1) vào (3)
(1+ SS22 )( 11−Γ 1b )
⇒Γ111c =S +
1− S22
(1+ S22 )(Γ−Γ 1ab 1 )
⇒Γ11ca = Γ +
1− S22
⇒ SSS22,( 12 . 21 )
Nếu mạng 2 cửa mang tính thuận nghịch: ⇒=SS12 21
Bài Tập:
a2
a1
Trở Kháng Trở Kháng
Chuẩn Z Chuẩn
0 Z0
b1
b2
ab12=
ab21=
⎛⎞01
⇒=S ⎜⎟
⎝⎠10
Bài Tập:
a2
a1
Trở Kháng Z Trở Kháng
Chuẩn Z Chuẩn
01 Z02
b1
b2
b1 Z11−+−ZZZZ 01 02 01
S11 ==Γ==11
aZZZZZ111+++010201
a2 =0
b2 Z22−+−ZZZZ 02 01 02
S22 ==Γ==22
aZZZZZ222+++020102
a1 =0
b2
S21 =
a1
a2 =0
6) Dịch Chuyển Mặt Phẳng Chuẩn Của Ma trận tán xạ [S]
l1 l2
l1 l2
II. Các Ma trận Đặc Tính Khác
1) Ma trận Trở Kháng
2) Ma trận Dẫn Nạp
3) Ma trận ABCD
VAVBI122= +
ICVDI122=+
⎡VV12⎤⎡⎤⎡⎤AB
⎢ ⎥⎢⎥= ⎢⎥
⎣ICDI12⎦⎣⎦⎣⎦
V I V I
A = 1 C = 1 B = 1 D = 1
V I
V2 2 I =0 2 V =0 I2
I2 =0 2 2 V2 =0
I1 I1a I2a I1b I2b I2
V V Mạng 2 Cửa V V Mạng 2 Cửa V V
1 1a a 2a 1b b 2b 2
⎡⎤⎡⎤⎡⎤AB AB AB
⎢⎥⎢⎥⎢⎥= .
⎣⎦⎣⎦⎣⎦CD CDab CD
Quan hệ giữa ma trận tán xạ [S] và Ma trận trở kháng [Z]
Quan hệ giữa ma trận tán xạ [S] và Ma trện dẫn nạp [Y]
Quan hệ giữa ma trận tán xạ [S] và Ma trận ABCD
AZ02 + B−− CZ01 Z 02 DZ 01
S11 =
AZ02 ++ B CZ01 Z 02 + DZ 01
A =+(1 SS11 − 22 −Δ SZZ)01 / 02 / 2 S 21
2(AD− BC ) Z Z
S = 01 02
BSSSZZS=+(1 11 + 22 +Δ)01 . 02 / 2 21 12
AZ02 ++ B CZ01 Z 02 + DZ 01
CSSSSZZ=−(1 11 − 22 −Δ) / 221 01 . 02
2 ZZ01 02
S21 =
DSSSZZS=−(1 11 + 22 −Δ)02 / 01 / 2 21 AZ02 ++ B CZ01 Z 02 + DZ 01
Δ=SSSSS11 12 − 12 21 −+−AZBCZZDZ02 01 02 + 01
S22 =
AZBCZZDZ02 ++01 02 + 01File đính kèm:
 bai_giang_ky_thuat_sieu_cao_tan_chuong_3_ma_tran_tan_xa_phan.pdf
bai_giang_ky_thuat_sieu_cao_tan_chuong_3_ma_tran_tan_xa_phan.pdf

