Bài giảng Kiến trúc máy tính - Chương: Biểu diễn số chấm động

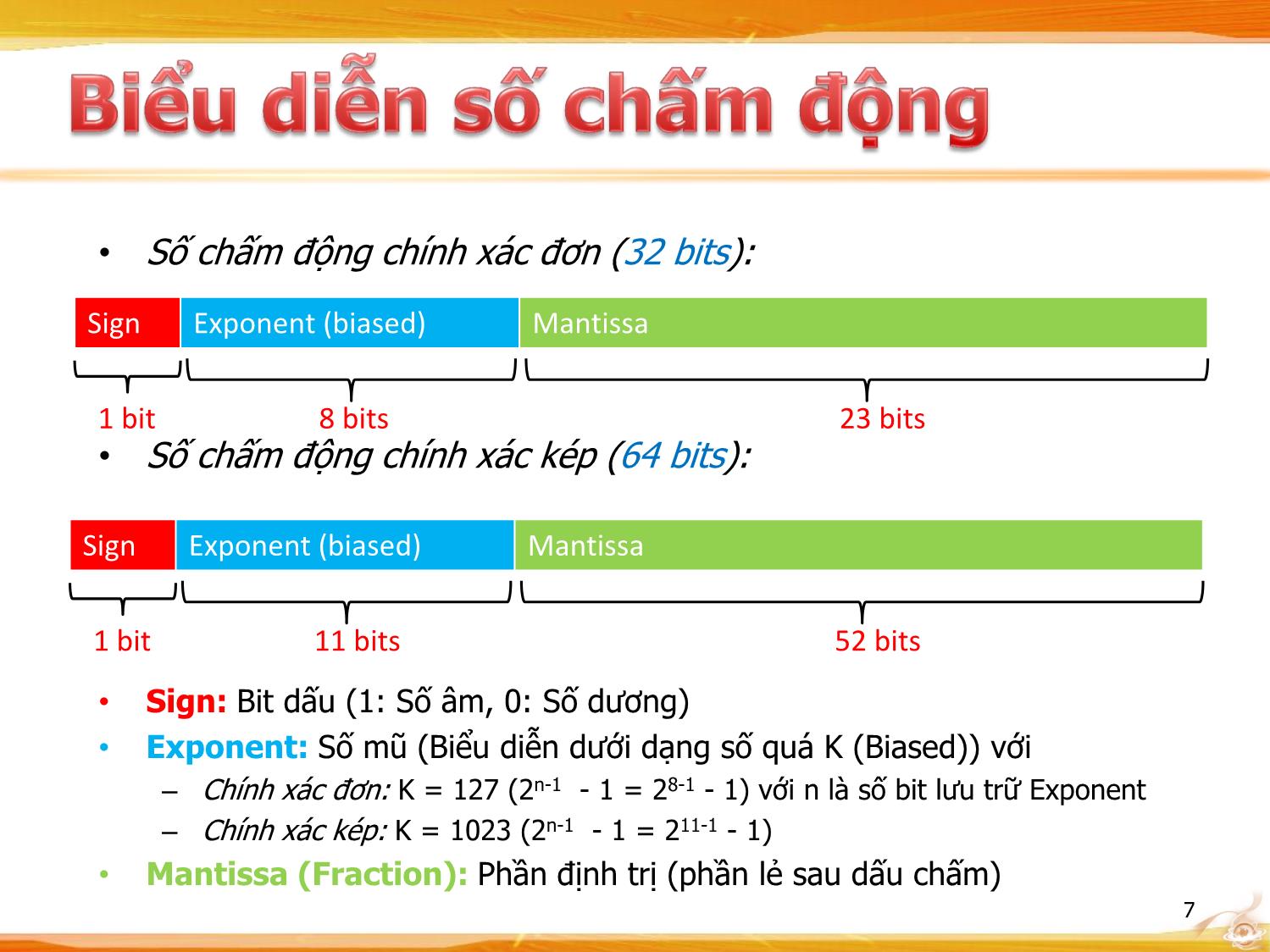
 1 
Môn học: Kiến trúc máy tính 
 • Biểu diễn số 123.37510 sang hệ nhị phân? 
 • Ý tưởng đơn giản: Biểu diễn phần nguyên và phần thập phân riêng lẻ 
 – Với phần nguyên: Dùng 8 bit ([010, 25510]) 
 12310 = 64 + 32 + 16 + 8 + 2 + 1 = 0111 10112 
 – Với phần thập phân: Tương tự dùng 8 bit 
 -2 -3
 0.375 = 0.25 + 0.125 = 2 + 2 = 0110 00002 
 123.37510 = 0111 1011.0110 00002 
 • Tổng quát công thức khai triển của số thập phân hệ nhị phân: 
 n 1 n 2 0 1 2 m
xn 1xn 2...x0.x 1x 2...x m xn 1.2 xn 2.2 ... x0.2 x 1.2 x 2.2 ... x m 2
 2 
• Tuy nhiênvới 8 bit: 
 – Phần nguyên lớn nhất có thể biểu diễn: 255 
 – Phần thập phân nhỏ nhất có thể biểu diễn: 2-8 ~ 10-3 = 0.001 
 Biểu diễn số nhỏ như 0.0001 (10-4) hay 0.000001 (10-
 5)? 
 Một giải pháp: Tăng số bit phần thập phân 
 – Với 16 bit cho phần thập phân: min = 2-16 ~ 10-5 
 – Có vẻ không hiệu quảCách tốt hơn ? 
 Floating Point Number (Số thực dấu chấm động) 
 3 
• Giả sử ta có số (ở dạng nhị phân) 
 -15 -16
 X = 0.00000000000000112 = (2 + 2 )10 
 14 số 0 
 -14 -1 -2 -14 -15 -16
 X = 0.112 * (2 )10 (= (2 + 2 ).2 = 2 + 2 ) 
 Thay vì dùng 16 bit để lưu trữ phần thập phân, ta có thể chỉ cần 6 bit: 
 X = 0.11 1110 
 Cách làm: Di chuyển vị trí dấu chấm sang phải 14 vị trí, dùng 4 bit để lưu 
 trữ số 14 này 
 Đây là ý tưởng cơ bản của số thực dấu chấm động (floating point number) 
 4 
• Trước khi các số được biểu diễn dưới dạng số 
 chấm động, chúng cần được chuẩn hóa về dạng: 
 ±1.M * 2E 
 – M: Phần thập phân không dấu (định trị) 
 – E: Phần số mũ (Exponent) 
• Ví dụ: 
 -4 
 – +0.0937510 = 0.000112 = +1.1 * 2
 2 
 – -5.2510 = 101.012 = -1.0101 * 2
 5 
• Có nhiều chuẩn nhưng hiện nay chuẩn IEEE 754 được 
 dùng nhiều nhất để lưu trữ số thập phân theo dấu chấm 
 động trong máy tính, gồm 2 dạng: 
 (slide sau) 
 6 
 • Số chấm động chính xác đơn (32 bits): 
 Sign Exponent (biased) Mantissa 
 1 bit 8 bits 23 bits 
 • Số chấm động chính xác kép (64 bits): 
Sign Exponent (biased) Mantissa 
 1 bit 11 bits 52 bits 
 • Sign: Bit dấu (1: Số âm, 0: Số dương) 
 • Exponent: Số mũ (Biểu diễn dưới dạng số quá K (Biased)) với 
 – Chính xác đơn: K = 127 (2n-1 - 1 = 28-1 - 1) với n là số bit lưu trữ Exponent 
 – Chính xác kép: K = 1023 (2n-1 - 1 = 211-1 - 1) 
 • Mantissa (Fraction): Phần định trị (phần lẻ sau dấu chấm) 
 7 
Biểu diễn số thực sau theo dạng số chấm động chính xác đơn (32 bit): X = -5.25 
• Bước 1: Đổi X sang hệ nhị phân 
 X = -5.2510 = -101.012 
• Bước 2: Chuẩn hóa theo dạng ±1.M * 2E 
 X = -5.25 = -101.01 = -1.0101 * 22 
• Bước 3: Biểu diễn Floating Point 
 – Số âm: bit dấu Sign = 1 
 – Số mũ E = 2 Phần mũ exponent với số thừa K=127 được biểu diễn: 
 Exponent = E + 127 = 2 + 127 = 12910 = 1000 00012 
 – Phần định trị = 0101 0000 0000 0000 0000 000 (Thêm 19 số 0 cho đủ 23 bit) 
 Kết quả nhận được: 1 1000 0001 0101 0000 0000 0000 0000 000 
 8 
• Số 0 (zero) 
 – Exponent = 0, Significand = 0 
• Số không thể chuẩn hóa (denormalized) 
 – Exponent = 0, Significand != 0 
• Số vô cùng (infinity) 
 – Exponent = 1111 (toàn bit 1), Significand = 0 
• Số báo lỗi (NaN – Not a Number) 
 – Exponent = 1111 (toàn bit 1), Significand != 0 
 9 
• Mã BCD dùng để biểu diễn hệ thập phân bằng các bit 
 nhị phân. Mã này thường được sử dụng trước khi qua 
 khối giải mã led 7 đoạn. 
• Mã BCD sử dụng 4 bit nhị phân tương ứng với 1 chữ số 
 thập phân. Ví dụ: 100112 = 1910 = 0001 1001BCD 
 Giải mã trên led 7 đoạn 
 10 
• Đặc điểm của mã Gray là 2 số có giá trị liền kề nhau thì khác 
 nhau 1 bit. Ta có bảng mã Gray 3 bit như sau: 
 Thập phân Nhị phân Gray 
 0 000 000 
 1 001 001 
 2 010 011 
 3 011 010 
 4 100 110 
 5 101 111 
 6 110 101 
 7 111 100 
 11