Bài giảng Kiến trúc máy tính - Chương 9: Bộ xử lý số học - Nguyễn Thị Phương
1. Đơn vị số học & logic (ALU)
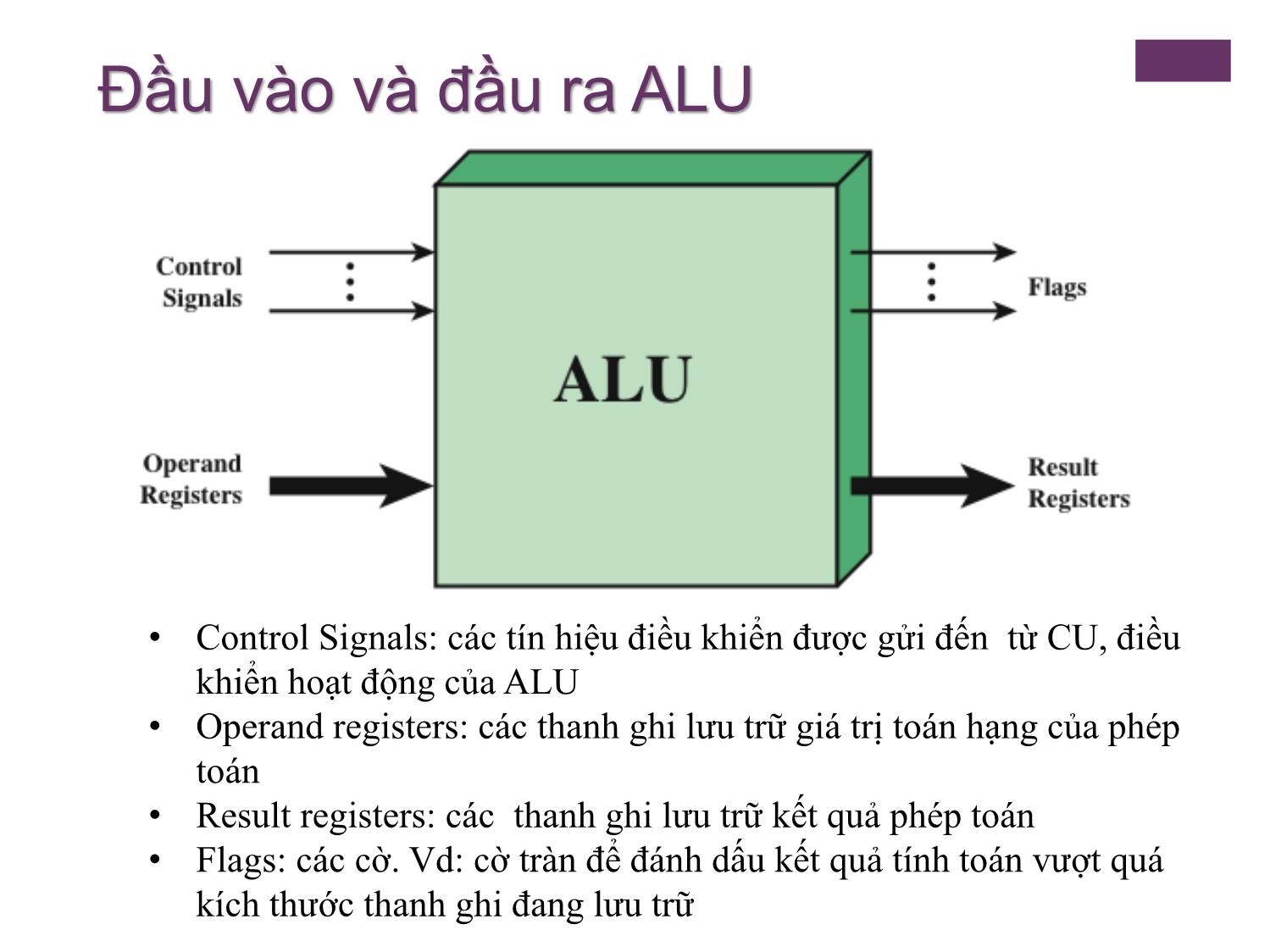
Phần của máy tính thực hiện phép toán số học và lôgíc
trên dữ liệu
Tất cả các bộ phận khác trong hệ thống máy tính (CU,
thanh ghi, bộ nhớ, I/O) đưa dữ liệu tới ALU để xử lý, sau
đó gửi lại kết quả
Khối ALU được thực hiện sử dụng các linh kiện logic số
có thể lưu trữ các số nhị phân và thực hiện các phép toán
logic Boolean đơn giản

Trang 1

Trang 2

Trang 3
Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Kiến trúc máy tính - Chương 9: Bộ xử lý số học - Nguyễn Thị Phương", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Kiến trúc máy tính - Chương 9: Bộ xử lý số học - Nguyễn Thị Phương

đảo ngược 0 1, 1 0) + Ví dụ 1 Biểu diễn các số sau sang dạng dấu-độ lớn 8b và bù 2-8b a) -128 b) 128 c) -54 d) 145 e) 11 f) -13 + b. Biểu diễn bù 2 (tiếp) Miền giá trị của từ mã n bit: −2푛−1 đến 2푛−1 − 1 Tính toán giá trị mã bù 2: Một số nguyên A, biểu diễn dưới dạng bù 2, n-bit: 풏− 풏− Nếu A là số dương Bit dấu 푛−1 có giá trị 0 Nếu A là số âm (A<0) Bit dấu 푛−1 có giá trị 1 Trong đó, 풊 là giá trị bit tại vị trí i + Hộp giá trị Bảng 10.2 Biểu diễn số nguyên 4-Bit Biểu diễn thập Biểu diễn dấu – độ Biểu diễn bù 2 phân lớn + Mở rộng phạm vi Trong một số trường hợp, ta muốn biểu diễn một số n-bit sang dạng biểu diễn m-bit ( > 푛): mở rộng phạm vi biểu diễn Trong biểu diễn dấu – độ lớn: di chuyển bit dấu tới vị trí mới ngoài cùng bên trái và điền (m-n) bit 0 vào sau bit dấu Biểu diễn số bù 2: Quy tắc: di chuyển bit dấu sang vị trí ngoài cùng bên trái và điền vào bằng bản sao bit dấu Đối với số dương, điền 0 vào, và số âm thì điền vào số 1 Đây được gọi là phần mở rộng dấu + Mở rộng phạm vi Ví dụ số bù 2 + Một số đặc điểm của biểu diễn bù 2 Miền giá trị (n bit) −2푛−1 đến 2푛−1 − 1 Biểu diễn số 0 1 cách Lấy bù của số dương tương ứng sau đó cộng thêm Biểu diễn số âm 1 Mở rộng chiều dài Điền giá trị dấu vào bên trái chuỗi bit Khi cộng hai số cùng dấu, nếu kết quả có dấu Luật tràn ngược lại tràn Luật trừ Khi trừ A cho B, lấy bù 2 của B sau đó cộng với A + 2. Phép toán trên số nguyên a. Phép đảo (phép phủ định) b. Phép cộng c. Phép trừ - luật trừ d. Phép nhân e. Phép chia + a. Phép đổi dấu (phép lấy âm) Quy tắc: Biểu diễn dấu – độ lớn: đảo bit dấu Biểu diễn bù 2: thực hiện phép toán bù 2 Đảo từng bit (kể cả bit dấu) Cộng 1 Đảo của đảo một số là chính nó + Số bù 2: xét hai trường hợp đặc biệt b. Phép cộng . Phép cộng được thực hiện bình thường như cộng hai số nhị phân . Trong một số trường hợp, xuất hiện thêm 1b (bit bôi đen) bỏ qua các bit này Nguyên tắc • Tràn ô nhớ: khi kết quả của một phép toán quá lớn vượt qua phạm vi biểu diễn của ô nhớ • Số bù 2: Tràn ô nhớ xảy ra nếu hai Tràn số cùng dấu cộng với nhau mà kết quả thu được lại là một số có dấu ngược với dấu của hai số đó + • Khi phát hiện tràn, ALU cần phải báo hiệu việc này để CPU không sử dụng kết quả c. Phép trừ Nguyên tắc NGUYÊN TẮC TRỪ: Lấy bù 2 (đảo) của số trừ và cộng với số bị trừ. Trừ + Phép trừ Mô tả hình học của số nguyên bù 2 Điểm đánh dấu tràn Hình 10.5 Mô tả hình học của số nguyên bù 2 Phần cứng thực hiện cộng và trừ • Thanh ghi A, B (A, B Register): lưu trữ hai số • Với phép trừ: thanh ghi B lưu trữ số trừ • Complementer: bộ lấy bù 2 • SW (switch): lựa chọn cộng hoặc trừ • Bộ cộng (Adder): thực hiện phép toán và đưa ra cờ tràn (nếu có) • Cờ tràn (OF-overflow bit): • 0: không tràn • 1: tràn • Kết quả có thể được lưu trữ ở thanh ghi thứ 3 hoặc một trong 2 thanh ghi A, B d. Phép nhân • So với phép cộng và phép trừ, phép nhân phức tạp hơn • Nhiều thuật toán tính toán phép nhân khác nhau đã được sử dụng trong các máy tính khác nhau • Trong phần này: i. Phép nhân giữa hai số nguyên không dấu ii. Phép nhân hai số biểu diễn bù 2 + i. Phép nhân giữa hai số nguyên không dấu Các bước bằng tay: • Tính các tích thành phần • Nếu số nhân là bit 0, tích thành phần bằng 0. Nếu số nhân là bit 1, tích thành phần là số bị nhân (multiplicand) • Tính tổng các tích thành phần (mỗi tích dịch trái đơn vị so với tích trước đó) • Tích của hai số n-bit là một số có kích thước 2n-bit + Thuật toán phép nhân nhị phân không dấu theo hướng máy tính Mô tả: Thanh ghi M: số bị nhân Thanh ghi Q: số nhân Thanh ghi 1bit C: ghi giá trị tràn của A+M (nếu có) Kết quả 2n-bit: thanh ghi A, Q + Ví dụ phép nhân nhị phân không dấu +ii. Phép nhân bù 2 . Số nguyên dương: nguyên tắc nhân giống số nguyên không dấu . Số nguyên âm: do có sự xuất hiện của bit dấu nên nguyên tắc trên không còn đúng nữa + Giải pháp 1 Sử dụng thuật toán nhân hai số không dấu: . Bước 1: Chuyển đổi số nhân và số bị nhân thành số dương tương ứng. . Bước 2: Nhân 2 số bằng thuật giải nhân số nguyên không dấu → được tích 2 số dương. . Bước 3: Hiệu chỉnh dấu của tích: . Nếu 2 thừa số ban đầu cùng dấu thì tích nhận được ở bước 2 là kết quả cần tính. . Nếu 2 thừa số ban đầu khác dấu nhau thì kết quả là số bù 2 của tích nhận được ở bước 2. Giải pháp 2: thuật toán Booth . Tốc độ tính toán nhanh hơn do số lượng phép toán ít hơn . Thuật toán chung cho cả số nguyên dương và âm + Thuật toán Booth + Giải thích thuật toán Ta có: 2i + 2i-1 + + 2j = 2i+1 – 2j (với i>=j) VD: M * 01110010 = M * (27 – 24 + 3) Quy tắc: duyệt từ trái sang phải: . Nếu gặp 10 thì trừ A đi M rồi dịch phải . Nếu gặp 01 thì cộng A với M rồi dịch phải . Nếu gặp 00 hay 11 thì chỉ dịch phải Ví dụ thuật toán Booth + e. Phép chia Phức tạp hơn phép nhân nhưng cũng sử dụng chung nguyên lý Thuật toán thực hiện phép chia hai số Bằng tay nguyên không dấu trong máy tính Số chia đặt trong thanh ghi M, số bị chia trong thanh ghi Q. A=0. Bộ đếm = n Tại mỗi bước: A và Q dịch trái 1 đơn vị Thực hiện − , nếu − ≥ 0 thì 푄0 = 1, A = − − < 0 thì 푄0 = 0 Giảm bộ đếm và quay trở lại thực hiện vòng lặp đến khi Bộ đếm = 0 + Lưu đồ thuật toán phép chia hai số nguyên không dấu + Chia số nguyên có dấu Bước 1: Chuyển đổi số chia và số bị chia thành số dương tương ứng Bước 2: Sử dụng thuật giải chia số nguyên không dấu để chia 2 số dương, kết quả nhận được là thương Q và phần dư R đều dương Bước 3: Hiệu chỉnh dấu kết quả theo quy tắc sau: + + Phép chia số bù 2 Tương tự như phép nhân, do có bit dấu nên phải có thuật toán khác: Giả sử số chia V và số bị chia D dương và < Nếu = : thương = 1, dư = 0. Nếu > : thương = 0, dư = D Thuật toán như sau: B1: Ghi số bù 2 của V vào thanh ghi M (M chứa số âm của V), ghi D vào thanh ghi A, Q, bộ đếm = n B2: Dịch A,Q sang trái 1 đơn vị B3: Tính A+M A B4: Kiểm tra: Nếu A dương (bit dấu = 0), 푄0 = 1 Nếu A âm (bit dấu =1), 푄0 = 0, khôi phục A lại giá trị trước đó B5: Giảm bộ đếm đi 1 đơn vị Lặp lại các bước từ 2 đến 5 cho đến khi bộ đếm = 0 Với các trường hợp V, D không dương, hiệu chỉnh kết quả dựa theo bảng ở trên + Ví dụ phép chia bù 2 + 4. Biểu diễn dấu chấm động a. Nguyên lý Quy ước: "dấu chấm" (point) được hiểu là kí hiệu ngăn cách giữa phần nguyên và phần lẻ của 1 số thực. Có 2 cách biểu diễn số thực trong máy tính: Số dấu chấm tĩnh (fixed-point number): Dấu chấm là cố định (số bit dành cho phần nguyên và phần lẻ là cố định) Hạn chế: không thể biểu diễn số rất lớn hoặc số thập phân rất nhỏ. Phần thập phân trong thương của một phép chia hai số lớn có thể bị mất Dùng trong các bộ vi xử lý hay vi điều khiển thế hệ cũ. Số dấu chấm động (floating-point number): Dấu chấm không cố định Dùng trong các bộ vi xử lý hiện nay, có độ chính xác cao hơn. + Biểu diễn số nhị phân dấu chấm động Một số nhị phân có thể được biểu diễn dưới dạng như sau: Trong đó: S: phần định trị B: cơ số E: số mũ Nếu B là một số định sẵn, ta chỉ cần lưu trữ S và E Vậy một số nhị phân có thể được lưu trữ trong máy tính với 3 trường sau: Dấu Giá trị S Số mũ E Định dạng dấu chấm động 32-bit Ví dụ: các số trên được lưu trữ như sau: B: ngầm định = 2 1 bit dấu: 0 nếu là số dương, 1 biểu diễn số âm 8 bit biased exponent: số mũ lệch Số mũ thực tế = số mũ lệch - độ lệch (độ lệnh = 2 −1 − 1, k: số bit phần mũ). Trong trường hợp này, độ lệch = 127 Số mũ thực tế nằm trong khoảng -127 đến +128 23 bit còn lại: phần định trị, được quy ước dạng 1.bbbbb...... Trong đó, số 1 đầu tiên là ngầm định + Biểu diễn số nhị phân dấu chấm động 32b S E M Hầu hết các hệ VXL có 3 loại định dạng nhị phân dấu chấm động (quy định theo chuẩn 754) 32b: 1b dấu (S), 8b phần mũ (E), 23b phần định trị (M) 64b: 1b dấu (S), 11b phần mũ (E), 52b phần định trị (M) 128b: 1b dấu, 15b phần mũ (E), 112b phần định trị (M) Trong đó: S: 0 nếu là số dương, 1 nếu là số âm E = số mũ thực tế + độ lệch (độ lệch = 2 −1 − 1, k là số bit phần mũ) M: phần định trị được chuẩn hóa dạng 1.bbbbb.bbbb + Chú ý: chuẩn hóa phần định trị Phần định trị có thể được biểu diễn thành nhiều dạng Các cách viết sau đây là tương đương, trong đó phần định trị được biểu diễn dưới dạng nhị phân: 0.110 * 25 110 * 22 0.0110 * 26 Quy ước biểu diễn: đưa về dạng 1.bbbbbbb.... Khi lưu trữ không cần lưu trữ phần nguyên, chỉ cần lưu trữ phần thập phân. Dấu chấm ngầm định ngay sau 8 bit phần số mũ + Ví dụ Chuyển số 23.5436 ra số nhị phân biểu diễn dạng dấu chấm động 32b B1: chuyển 23.5436 ra số nhị phân: 10111.1001101 (xấp xỉ) ퟒ B2: chuẩn hóa: . 풙 B3: Biểu diễn dạng dấu chấm động: + Ví dụ 1 Biểu diễn số thực X = 0.375 về dạng số dấu chấm động theo chuẩn IEEE 754 dạng 32 bit Ví dụ 2 Có một số thực X có dạng biểu diễn nhị phân theo chuẩn IEEE 754 dạng 32 bit như sau: 1100 0001 0101 0110 0000 0000 0000 0000. Xác định giá trị thập phân của số thực đó. Ví dụ 3 Xác định giá trị thập phân của số thực X có dạng biểu diễn theo chuẩn IEEE 754 dạng 32 bit như sau: 0011 1111 1000 0000 0000 0000 0000 0000 + Miền giá trị + Mật độ số dấu phẩy động b. Chuẩn IEEE 754 Hiệp hội IEEE đã chuẩn hóa cho việc biểu diễn số dấu phẩy động nhị phân trong máy tính Mục đích: . Hỗ trợ tính di động của chương trình từ bộ xử lý này sang bộ xử lý khác . Khuyến khích phát triển các chương trình định hướng số học tinh vi hơn Chuẩn được công nhận rộng rãi và được sử dụng trên hầu hết các bộ VXL và bộ tính toán số học hiện đại IEEE 754-2008 quy định các định dạng biểu diễn dấu phẩy động nhị phân và thập phân Trong phần này chỉ đề cập đến dạng biểu diễn dấu phẩy động nhị phân + IEEE 754-2008 IEEE 754-2008 định nghĩa 3 định dạng dấu chấm động sau: Định dạng số học Được sử dụng để biểu diễn các toán hạng hoặc kết quả phép toán dưới dạng dấu chấm động. Định dạng cơ bản: quy định 5 dạng biểu diễn dấu chấm động: Ba cho số nhị phân: chiều dài 32b, 64b và 128b Hai cho thập phân: chiều dài 64b và 128b Định dạng chuyển đổi Đưa ra dạng mã hoá nhị phân độ dài cố định cho phép trao đổi dữ liệu giữa các nền tảng khác nhau và có thể được sử dụng để lưu trữ. Định dạng IEEE 754 Cơ số R = 2 Có các dạng cơ bản: . Dạng 32-bit: 1b dấu, 8b mũ, 23b định trị . Dạng 64-bit: 1b dấu, 11b mũ, 52b định trị . Dạng 128-bit: 1b dấu, 15b mũ, 112b định trị Bảng 10.3 Thông số định dạng chính trong chuẩn IEEE 754 *không bao gồm bit ngầm định và bit dấu + IEEE754: Một số quy ước đặc biệt Nếu tất cả các bit của phần số mũ đều bằng 0, các bit của phần định trị đều bằng 0, thì X = ± 0 Ví dụ: định dạng 32b: +010 = 0 00000000 00000000000000000000000 −010 = 1 00000000 00000000000000000000000 Nếu tất cả các bit của phần mũ đều bằng 1, các bit của phần định trị đều bằng 0, thì X = ± ∞ Ví dụ: định dạng 32b: +∞ = 0 11111111 00000000000000000000000 −∞ = 1 11111111 00000000000000000000000 Nếu tất cả các bit của phần mũ đều bằng 1, phần định trị có ít nhất một bit bằng 1, thì X biểu diễn một giá trị quy ước NaN (not a number) NaN sinh ra bởi một số phép toán dấu chấm động đặc biệt, vd: ±∞/±∞ Có hai loại NaN: quiet NaN và signalling NaN + Các định dạng bổ sung Extended Precision Formats Extendable Precision Format Cung cấp các bit bổ sung trong số Độ chính xác và phạm vi được xác mũ (phạm vi mở rộng) và trong định dưới sự kiểm soát của người phần định trị (độ chính xác mở dùng rộng) Có thể được sử dụng để tính toán Giảm khả năng kết quả cuối cùng bị tồi đi do sai số làm tròn quá mức trung gian nhưng chuẩn sẽ không có ràng buộc hoặc định dạng hoặc Giảm bớt khả năng tràn trung gian chiều dài làm hủy bỏ phép tính có kết quả cuối cùng có thể biểu diễn được dưới định dạng cơ bản Có một số lợi ích của định dạng cơ bản rộng hơn mà không phải chịu chi phí thời gian khi muốn độ chính xác cao hơn + 5 Các phép toán với số dấu chấm động a. Phép toán cộng và trừ Cộng và trừ dấu phẩy động + Bốn bước cơ bản của thuật toán cộng và trừ Kiểm tra các số hạng có bằng 0 hay không Nếu có thì gán kết quả dựa trên số còn lại. Hiệu chỉnh phần định trị Sao cho 2 số có phần mũ giống nhau: tăng số mũ nhỏ và dịch phải phần định trị tương ứng (dịch phải để hạn chế sai số nếu có). 3 3 3 VD: 1.01 * 2 + 1.11 = 1.01 * 2 + 0.00111 * 2 Cộng hoặc trừ phần định trị Nếu tràn thì dịch phải và tăng số mũ, nếu bị tràn số mũ thì báo lỗi tràn số. Chuẩn hóa kết quả Dịch trái phần định trị để bit trái nhất (bit MSB) khác 0. Tương ứng với việc giảm số mũ nên có thể dẫn đến hiện tượng tràn dưới số mũ. + Các khả năng tràn số Phép toán cộng hoặc trừ có thể gây ra một số khả năng tràn như sau: Tràn trên số mũ (Exponent Overflow): mũ dương vượt ra khỏi giá trị cực đại của số mũ dương có thể. Tràn dưới số mũ (Exponent Underflow): mũ âm vượt ra khỏi giá trị cực đại của số mũ âm có thể. Tràn trên phần định trị (Mantissa Overflow): cộng hai phần định trị có cùng dấu, kết quả bị nhớ ra ngoài bit cao nhất. Tràn dưới phần định trị (Mantissa Underflow): Khi hiệu chỉnh phần định trị, các số bị mất ở bên phải phần định trị. + b. Phép nhân dấu chấm động • Bộ nhân phần định trị được thực hiện giống như thuật toán nhân hai số nhị phân thông thường. • Kết quả sẽ có kích thước lớn gấp đôi, tuy nhiên giá trị sẽ được chuẩn hóa theo dạng biểu diễn + c. Phép chia dấu chấm động + Nhân và chia dấu chấm động Các bước cơ bản 1. Kiểm tra 0 2. Cộng/trừ số mũ (có thể xảy ra tràn kiểm tra tràn mũ) 3. Nhân/chia các định trị 4. Chuẩn hóa 5. Làm tròn + Câu hỏi chương 9 1. Giải thích ngắn gọn về các biểu diễn: dấu-độ lớn, bù 2. 2. Cách xác định một số là âm hay dương trong các biểu diễn: dấu-độ lớn, bù 2. 3. Nguyên tắc mở rộng phạm vi biểu diễn số cho biểu diễn bù 2 là gì? 4. Cách đảo một số nguyên trong biểu diễn bù 2? 5. Phân biệt biểu diễn bù 2 của một số và bù 2 của một số? 6. Nếu coi 2 số bù 2 như là số nguyên không dấu khi thực hiện cộng, kết quả hiểu theo số bù 2 là chính xác. Điều này không đúng với phép nhân. Tại sao? 7. Bốn thành phần của một số trong biểu diễn dấu chấm động là gì? 8. Vì sao sử dụng biểu diễn bias cho số mũ của một số dấu chấm động? 9. Phân biệt tràn số mũ, và tràn định trị? 10. Các yếu tố cơ bản của phép cộng và trừ dấu chấm động là gì?
File đính kèm:
 bai_giang_kien_truc_may_tinh_chuong_9_bo_xu_ly_so_hoc_nguyen.pdf
bai_giang_kien_truc_may_tinh_chuong_9_bo_xu_ly_so_hoc_nguyen.pdf

