Bài giảng Kiến trúc máy tính 1 - Chương 3: Biểu diễn dữ liệu - Vũ Đức Lung
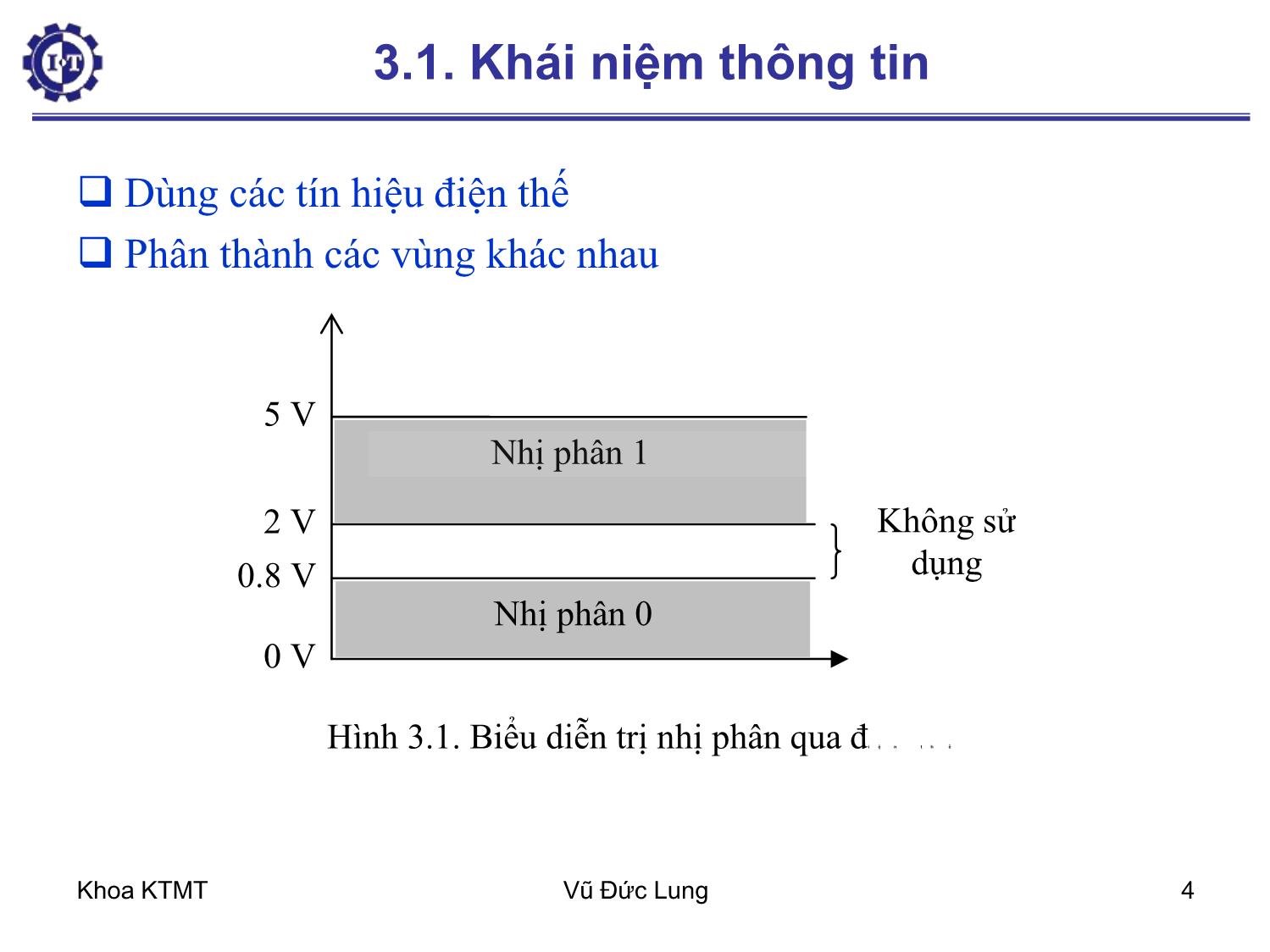
3.1. Khái niệm thông tin
3.2. Lượng thông tin và sự mã hóa thông tin
3.3. Hệ thống số
3.4. Các phép tính số học cho hệ nhị phân
3.5. Số quá n (excess-n)
3.6. Cách biểu diễn số với dấu chấm động
3.7. Biểu diễn số BCD
3.8. Biểu diễn các ký tự

Trang 1

Trang 2

Trang 3
Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Kiến trúc máy tính 1 - Chương 3: Biểu diễn dữ liệu - Vũ Đức Lung", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Kiến trúc máy tính 1 - Chương 3: Biểu diễn dữ liệu - Vũ Đức Lung

Khoa KTMT Vũ Đức Lung 1 Chương 3 – Biểu diễn dữ liệu 3.1. Khái niệm thông tin 3.2. Lượng thông tin và sự mã hóa thông tin 3.3. Hệ thống số 3.4. Các phép tính số học cho hệ nhị phân 3.5. Số quá n (excess-n) 3.6. Cách biểu diễn số với dấu chấm động 3.7. Biểu diễn số BCD 3.8. Biểu diễn các ký tự Khoa KTMT Vũ Đức Lung 2 Mục tiêu Hiểu các hệ cơ số thông dụng và cách chuyển đổi. Hiểu phương pháp biểu diễn số nguyên và số chấm động. Hiểu các phương pháp tính đơn giản với các số. Hiểu các phương pháp biểu diễn số BCD và ký tự Khoa KTMT Vũ Đức Lung 3 Hình dung về “biểu diễn dữ liệu” Mọi thứ trong máy tính đều là 0 và 1 Thế giới bên ngoài có nhiều khái niệm như con số, chữ cái, hình ảnh, âm thanh, → biểu diễn dữ liệu = quy tắc “gắn kết” các khái niệm trong thế giới thật với một dãy số 0 và 1 trong máy tính Khoa KTMT Vũ Đức Lung 4 3.1. Khái niệm thông tin Dùng các tín hiệu điện thế Phân thành các vùng khác nhau 5 V 2 V 0.8 V 0 V Nhị phân 1 Nhị phân 0 Không sử dụng Hình 3.1. Biểu diễn trị nhị phân qua đi ệ n t h ế Khoa KTMT Vũ Đức Lung 5 3.2. Lượng thông tin và sự mã hoá thông tin Thông tin được đo lường bằng đơn vị thông tin mà ta gọi là bit. Lượng thông tin được định nghĩa bởi công thức: I = Log2(N) – Trong đó: • I: là lượng thông tin tính bằng bit • N: là số trạng thái có thể có – Ví dụ, để biểu diễn một trạng thái trong 8 trạng thái có thể có, ta cần một số bit ứng với một lượng thông tin là: I = Log2(8) = 3 bit Khoa KTMT Vũ Đức Lung 6 3.3. Hệ Thống Số Dạng tổng quát để biểu diễn giá trị của một số: – Trong đó: • Vk: Số cần biểu diễn giá trị • m: số thứ tự của chữ số phần lẻ (phần lẻ của số có m chữ số được đánh số thứ tự từ -1 đến -m) • n-1: số thứ tự của chữ số phần nguyên (phần nguyên của số có n chữ số được đánh số thứ tự từ 0 đến n-1) • bi: giá trị của chữ số thứ i • k: hệ số (k=10: hệ thập phân; k=2: hệ nhị phân;...). 1 . n mi i ik kbV Khoa KTMT Vũ Đức Lung 7 3.3. Hệ Thống Số Các hệ đếm (cơ số) thông dụng – Thập phân (Decimal) • 10 chữ số : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 – Nhị phân (Binary) • 2 chữ số: 0, 1 – Bát phân (Octal) • 8 chữ số: 0, 1, 2, 3, 4, 5, 6, 7 – Thập lục phân (Hexadecimal) • 16 chữ số: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E. – A=10, B=11, C=12, D=13, E=14, F=15 Khoa KTMT Vũ Đức Lung 8 Chuyển đổi từ cơ số 10 sang b Quy tắc: Chia số cần đổi cho b, lấy kết quả chia tiếp cho b cho đến khi kết quả bằng 0. Số ở cơ số b chính là các số dư (của phép chia) viết ngược. Ví dụ: 41 2 = 20 dư 1 20 2 = 10 dư 0 10 2 = 5 dư 0 5 2 = 2 dư 1 2 2 = 1 dư 0 1 2 = 0 dư 1 4110 = 1010012 Khoa KTMT Vũ Đức Lung 9 Chuyển đổi hệ 10 sang Nhị phân Quy tắc: Người ta chuyển đổi từng phần nguyên và lẻ theo quy tắc sau Phần nguyên: Chia liên tiếp phần nguyên cho 2 giữ lại các số dư, Số nhị phân được chuyển đổi sẽ là dãy số dư liên tiếp tính từ lần chia cuối về lần chia đầu tiên. Phần lẻ: Nhân liên tiếp phần lẻ cho 2, giữ lại các phần nguyên được tạo thành. Phần lẻ của số Nhị phân sẽ là dãy liên tiếp phần nguyên sinh ra sau mỗi phép nhân tính từ lần nhân đầu đến lần nhân cuối Khoa KTMT Vũ Đức Lung 10 Ví dụ: Chuyển sang hệ Nhị phân số: 13,6875 Thực hiện: Phần nguyên: 13:2 = 6 dư 1 6:2 = 3 dư 0 3:2 = 1 dư 1 1:2 = 0 dư 1 Phần nguyên của số Nhị phân là 1101 Phầnlẻ: 0,6875 x 2 = 1,375 Phần nguyên là 1 0,375 x 2 = 0,750 Phần nguyên là 0 0,750 x 2 = 1,500 Phần nguyên là 1 0,5 x 2 = 1,00 Phần nguyên là 1 Phần lẻ của số Nhị phân là: 0,1011 Ta viết kết quả là: (13,625)10 = (1101,1011)2 Chuyển đổi hệ 10 sang Nhị phân Khoa KTMT Vũ Đức Lung 11 Chuyển đổi từ cơ số 10 sang b Quy tắc: Chia số cần đổi cho b, lấy kết quả chia tiếp cho b cho đến khi kết quả bằng 0. Số ở cơ số b chính là các số dư (của phép chia) viết ngược. Ví dụ: 41 16 = 2 dư 9 2 16 = 0 dư 2 4110 = 2916 Khoa KTMT Vũ Đức Lung 12 Ví dụ: Chuyển số (3287,5100098)10 sang Cơ số 8. Phần nguyên: 3287:8 = 410dư 7 410:8 = 51 dư 2 51:8= 6 dư 3 6:8 = 0 dư 6 Vậy (3287)10=(6327)8 Phần lẻ: 0,5100098x8 = 4,0800784 phần nguyên là 4 0,0800784x8= 0,6406272 phần nguyên là 0 0,6406270x8= 5,1250176 phần nguyên là 5 0,1250176x8= 1,0001408 phần nguyên là 1 Vậy (0,5100098)10=(0,4051)8 Kết quả chung là: (3287,5100098)10 =(6327,4051)8 Khoa KTMT Vũ Đức Lung 13 Chuyển đổi hệ 2 sang hệ 10 Ví dụ: Chuyển đổi sang hệ Thập phân số: m = 1101,011 Thực hiện: Ta lập tổng theo trọng số của từng Bit nhị phân: m = 1.23 + 1.22 + 0.21 + 1.20 + 0.2-1 + 1.2-2 + 1.2-3 m = 8 + 4 + 0 + 1 + 0 + 1/4 + 1/8 m = 13,375 Khoa KTMT Vũ Đức Lung 14 Chuyển đổi cơ số 2-8-16 Quy tắc: Từ phải sang trái, gom 3 chữ số nhị phân thành một chữ số bát phân hoặc gom 4 chữ số nhị phân thành một chữ số thập lục phân Khoa KTMT Vũ Đức Lung 15 Ví dụ: Chuyển số M = (574,321)8 sang biễu diễn nhị phân. Thực hiện: Thay mỗi chữ số bằng nhóm nhị phân 3 bit tương ứng: M = 101 111 100 , 011 010 001 5 7 4 3 2 1 Ví dụ: Chuyển số M = (1001110,101001)2 sang cơ số 8. Thực hiện: M = 1 001 110 , 101 001 M = 1 1 6 , 5 1 M = (116,51)8 Khoa KTMT Vũ Đức Lung 16 Số bù Quy tắc chung (r: cơ số, n: số chữ số) – Bù (r-1) của N = (rn – 1) – N – Bù r của N = rn – N • Bù r của (bù r của N) = N • Nhận xét: Có tính chất giống – (– N) = N Đối với hệ nhị phân: – Bù 1 = đảo n bit của N • Bù 1 của (1100) = 0011 – Bù 2 = bù 1 + 1 • Bù 2 của (1100) = 0011 + 1 = 0100 • Mẹo: giữ nguyên các số 0 bên phải cho đến khi gặp số 1, sau đó đảo 1100 0100 Khoa KTMT Vũ Đức Lung 17 Số quá n (excess-n) 000 001 010 011 100 101 110 111 0 1 2 3 4 5 6 7 000 001 010 011 100 101 110 111 -3 -2 -1 0 1 2 3 4 Nguyên dương Quá 3 Quy tắc chung: Biểu diễn quá n của N = biểu diễn nguyên dương của (N + n) Ví dụ: Biểu diễn (quá 127) của 7 là: 127+7 = 134 = 100001102 Khoa KTMT Vũ Đức Lung 18 Cộng trừ số nhị phân nguyên Quy tắc: -A = bù 2 của A A – B = A + (-B) = A + (bù 2 của B) Ví dụ: 13 – 6 = 13 + (-6) 6 = 00000110 -6 = 11111010 13 = 00001101 = 00000111 (7)1 Bỏ bit tràn (nếu có) Khoa KTMT Vũ Đức Lung 19 BCD (Binary Coded Decimal) Biểu diễn một chữ số thập phân bằng 4 chữ số nhị phân (ít dùng) 0 = 0000 1 = 0001 9 = 1001 Khoa KTMT Vũ Đức Lung 20 Biểu diễn ký tự Sử dụng bộ mã ASCII mở rộng (8 bit) – 00 – 1F: ký tự điều khiển – 20 – 7F: ký tự in được – 80 – FF: ký tự mở rộng (ký hiệu tiền tệ, vẽ khung, ) Ngày nay dùng bộ mã Unicode (16 bit) (UTF-8) Khoa KTMT Vũ Đức Lung 21 Biểu diễn chấm động F = (-1)S M RE – S: dấu – M: định trị – R: cơ số – e: mũ Ví dụ: 2006 = (-1)0 2.006 103 Khoa KTMT Vũ Đức Lung 22 Biểu diễn chấm động Biểu diễn chấm động được gọi là chuẩn hóa khi phần định trị chỉ có duy nhất một chữ số bên trái dấu chấm thập phân và chữ số đó khác không → một số chỉ có duy nhất một biểu diễn chấm động được chuẩn hóa. 2.006 103 (chuẩn) 20.06 102 (không) 0.2006 104 (không) Khoa KTMT Vũ Đức Lung 23 Biểu diễn chấm động trên hệ nhị phân Sử dụng dạng chuẩn hóa Dùng 1 bit cho phần dấu: 0-dương, 1-âm Không biểu diễn cơ số (R) vì luôn bằng 2 Phần định trị chỉ biểu diễn phần lẻ (bên phải dấu chấm) vì chữ số bên trái dấu chấm luôn là 1 Khoa KTMT Vũ Đức Lung 24 Biểu diễn chấm động trên hệ nhị phân Ví dụ: – Dấu 1 bit – Mũ: 8 bit (từ bit 23 đến bit 30) là một số quá 127 (sẽ có trị từ -127 đến 128) – Định trị: 23 bit (từ bit 0 đến bit 22) 022233031 Khoa KTMT Vũ Đức Lung 25 Biểu diễn chấm động trên hệ nhị phân Ví dụ: 209.812510 = 11010001.11012 = 1.10100011101 27 Biểu diễn (quá-127) của 7 là: 127+7 = 134 = 100001102 Kết quả: 0 10000110 1010001110100000000000 022233031 Lưu ý không có số 1 bên trái dấu chấm
File đính kèm:
 bai_giang_kien_truc_may_tinh_1_chuong_3_bieu_dien_du_lieu_vu.pdf
bai_giang_kien_truc_may_tinh_1_chuong_3_bieu_dien_du_lieu_vu.pdf

