Bài giảng Giải tích II - Chương 2: Đạo hàm, vi phân - Nguyễn Văn Quang
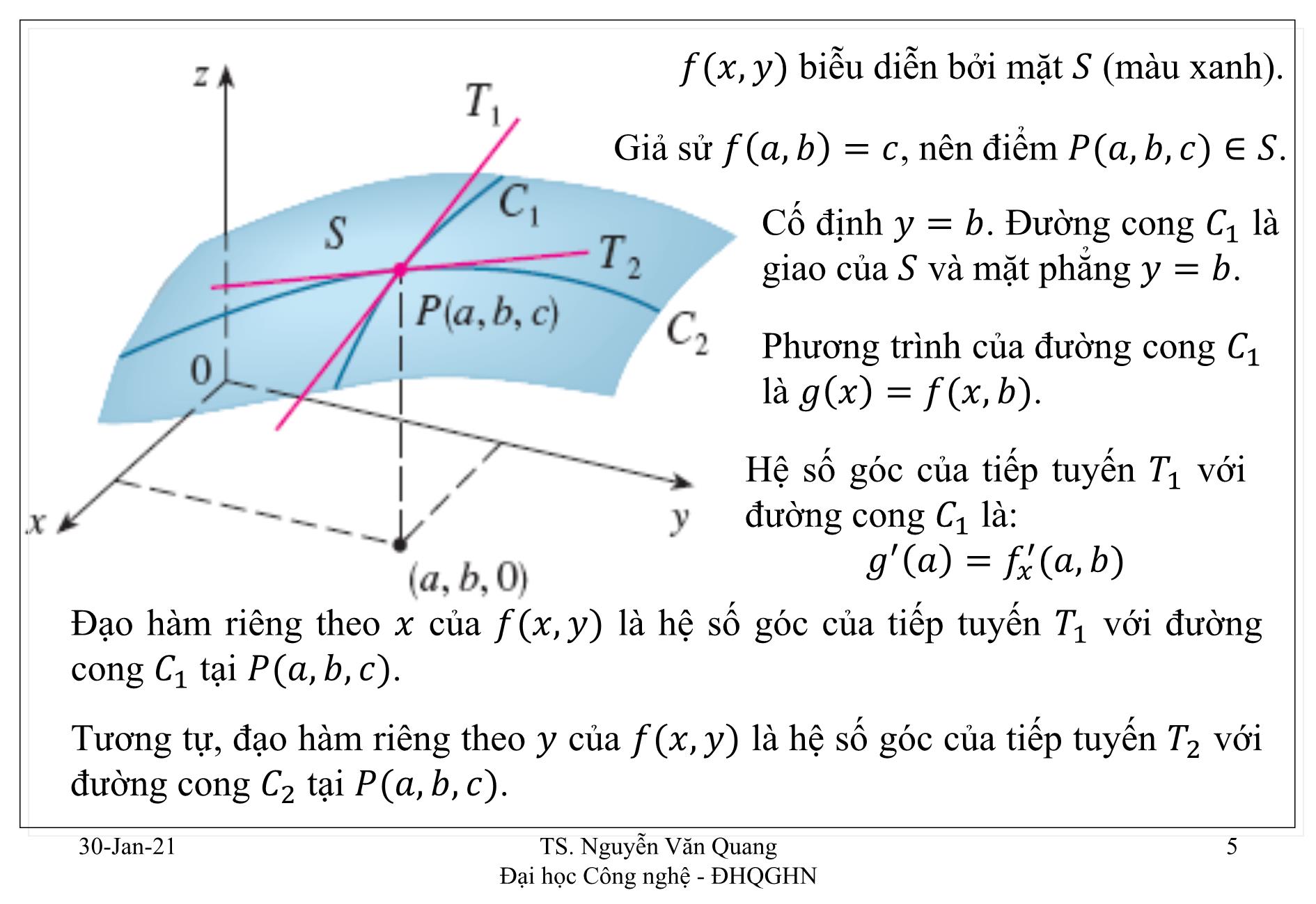
𝑓(𝑥, 𝑦) biễu diễn bởi mặt 𝑆 (màu xanh).
Giả sử 𝑓 𝑎, 𝑏 = 𝑐, nên điểm 𝑃(𝑎, 𝑏, 𝑐) ∈ 𝑆.
Cố định 𝑦 = 𝑏. Đường cong 𝐶1 là
giao của 𝑆 và mặt phẳng 𝑦 = 𝑏.
Phương trình của đường cong 𝐶1
là 𝑔 𝑥 = 𝑓(𝑥, 𝑏).
Hệ số góc của tiếp tuyến 𝑇1 với
đường cong 𝐶1 là:
𝑔′ 𝑎 = 𝑓𝑥′(𝑎, 𝑏)
Đạo hàm riêng theo 𝑥 của 𝑓(𝑥, 𝑦) là hệ số góc của tiếp tuyến 𝑇1 với đường
cong 𝐶1 tại 𝑃(𝑎, 𝑏, 𝑐).
Tương tự, đạo hàm riêng theo 𝑦 của 𝑓(𝑥, 𝑦) là hệ số góc của tiếp tuyến 𝑇2 với
đường cong 𝐶2 tại 𝑃(𝑎, 𝑏, 𝑐).

Trang 1

Trang 2

Trang 3

Trang 4
Trang 5

Trang 6
Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Giải tích II - Chương 2: Đạo hàm, vi phân - Nguyễn Văn Quang", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Giải tích II - Chương 2: Đạo hàm, vi phân - Nguyễn Văn Quang

p 1, cấp 2 tại (0,0) đều bằng 0 do đó: f(,)() x y o 2 2 xsin y y sin x o Vậy: lim lim 0 (,)(0,0)x y xy2 2 (,)(0,0) x y 2 30-Jan-21 TS. Nguyễn Văn Quang 97 Đại học Công nghệ - ĐHQGHN Ví dụ xsin y y sin x Tính giới hạn: lim (xy , ) (0,0) xy22 Cách 2: Sử dụng khai triển hàm một biến: 33 yx33 x y o y y x o x 3! 3! f(,) x y xy22 xy x2 y 2 x o y 3 y o x 3 xy22 3! xy22 30-Jan-21 TS. Nguyễn Văn Quang 98 Đại học Công nghệ - ĐHQGHN Ví dụ xsin y y sin x Tính giới hạn: lim (xy , ) (0,0) xy22 22 Ta có: xy x y xy22 0 0,(xy , ) (0,0) xy22 3! 2 3! xoy 3 yox 3 xoy 3 yox 3 xoy 3 yox 3 0 x22 y2 xy 2 xy 2 xy o y33 o x 0,(xy , ) (0,0) . Do đó: limf ( x , y ) 0 22yx (xy , ) (0,0) 30-Jan-21 TS. Nguyễn Văn Quang 99 Đại học Công nghệ - ĐHQGHN Cực trị không điều kiện Định nghĩa Hàm f f (,) x y đạt cực đại địa phương tại , nếu tồn tại một lân cận của (,):(,)(,)x0 y 0 f x y f x 0 y 0 , với mọi ( , ) thuộc lân cận đó. Tức là: BMr ( 0 ,): MBMrfM ( 0 ,):() fM ( 0 ). Định nghĩa tương tự cho cực tiểu địa phương. Điểm dừng: các đạo hàm riêng cấp 1 bằng 0. Điểm tới hạn: các đạo hàm riêng cấp 1 bằng 0 hoặc không tồn tại. Điểm cực trị: hàm đạt cực đại địa phương hoặc cực tiểu địa phương. 30-Jan-21 TS. Nguyễn Văn Quang 100 Đại học Công nghệ - ĐHQGHN Ví dụ Hàm ( , ) = 2 + 2 đạt cực tiểu tại (0,0). Xét f ( x , y ) f (0,0) x22 y 0 f(,) x y x22 y 0 (,)(0,0) x y Vậy điểm (0,0) là điểm cực tiểu. 30-Jan-21 TS. Nguyễn Văn Quang 101 Đại học Công nghệ - ĐHQGHN Ví dụ Khảo sát cực trị của f ( x , y ) 1 ( x 1) 22 ( y 1) tại (1,1). f( x , y ) f (1,1) 1 ( x 1)22 ( y 1) 1 (xy 1)22 ( 1) 0 f( x , y ) f (1,1) f( x , y ) 1 ( x , y ) (1,1) Vậy hàm đạt cực đại tại (1,1). 30-Jan-21 TS. Nguyễn Văn Quang 102 Đại học Công nghệ - ĐHQGHN Ví dụ Khảo sát cực trị của ( , ) = 2 tại điểm (0,0). Hàm không đạt cực trị tại (0,0). Nếu dần về (0,0) theo đường thẳng y = x (x > 0) thì f (x,y) > 0. Nếu dần về (0,0) theo đường thẳng y = x (x < 0) thì f (x,y) < 0. Trong mọi lân cận của (0,0) đều tìm được điểm (x,y) mà f (x,y) > 0 và điểm (x,y) mà f (x,y) < 0. 30-Jan-21 TS. Nguyễn Văn Quang 103 Đại học Công nghệ - ĐHQGHN Cực trị không điều kiện Định lý điều kiện cần của cực trị Hàm f đạt cực trị tại M 0 (,) x 0 y 0 thì tại đó: 1) Không tồn tại đạo hàm riêng cấp 1, hoặc 2) fxy ( x0 , y 0 ) 0, f ( x 0 , y 0 ) 0 30-Jan-21 TS. Nguyễn Văn Quang 104 Đại học Công nghệ - ĐHQGHN Cực trị không điều kiện Định lý điều kiện đủ của cực trị Cho M 0 (,) x 0 y 0 là điểm dừng của hàm = ( , ) và có các đạo hàm riêng liên tục đến cấp 2 trong lân cận của điểm 0. 2 1) 0 > 0: 0 là điểm cực tiểu. 2 2) 0 < 0: 0 là điểm cực đại. 2 3) 0 không xác định dấu thì 0 không phải là điểm cực trị. 30-Jan-21 TS. Nguyễn Văn Quang 105 Đại học Công nghệ - ĐHQGHN Cực trị không điều kiện Sơ đồ khảo sát cực trị của hàm hai biến = ( , ): fx ( x , y ) 0 1) Tìm điểm dừng P( x , y ), P ( x , y ), 1 1 1 2 2 2 fy ( x , y ) 0 2) Tính tất cả các đạo hàm riêng cấp hai f xx ,,. f xy f yy 3) Khảo sát từng điểm dừng. 2 P1(,): x 1 y 1 A fxx ( P1 ), B f xy ( P 1 ), C f yy ( P 1 ), AC B 0 0 P1 là điểm cực tiểu P1 là điểm cực đại A 0 A 0 0: chưa kết luận được 0 P không là điểm cực trị 1 phải khảo sát bằng định nghĩa 30-Jan-21 TS. Nguyễn Văn Quang 106 Đại học Công nghệ - ĐHQGHN Cực trị không điều kiện Chú ý: 1) Sơ đồ này không cho phép khảo sát cực trị tại điểm mà các đạo hàm riêng không tồn tại (điểm tới hạn, nhưng không phải là điểm dừng). Những điểm này phải khảo sát bằng định nghĩa. 2) Sơ đồ này chỉ áp dụng cho hàm hai biến. 30-Jan-21 TS. Nguyễn Văn Quang 107 Đại học Công nghệ - ĐHQGHN Ví dụ Khảo sát cực trị của hàm: f ( x , y ) x 22 xy y 2 x y f 2 x y 2 0 1) Tìm điểm dừng: x P (1,0) 1 fy x 2 y 1 0 2) Tìm đạo hàm riêng cấp 2: f xx 2, f xy 1, f yy 2 3) Khảo sát từng điểm dừng: P1(1,0) : A fxx ( P 1 ) 2; B f xy ( P 1 ) 1 2 C fyy ( P1 ) 2; AC B 3 0 0 Kết luận cho điểm dừng P1: P 1 là điểm cực tiểu, f ct f ( P 1 ) 1 A 0 30-Jan-21 TS. Nguyễn Văn Quang 108 Đại học Công nghệ - ĐHQGHN Ví dụ Khảo sát cực trị của hàm: f ( x , y ) x 4 y 4 x 2 2 xy y 2 3 fx 4 x 2 x 2 y 0 1) Tìm điểm dừng: PPP(1,1), ( 1, 1), (0,0) 3 1 2 3 fy 4 y 2 x 2 y 0 22 2) Tìm đạo hàm riêng cấp 2: fxx 12 x 2, f xy 2, f yy 12 y 2 3) Khảo sát từng điểm dừng: P 11 (1,1) : A fxx ( P ) 10; B 2 22 C fyy ( P1 ) 10; AC B 10 4 0 0 Kết luận cho điểm dừng P1: P 1 là điểm cực tiểu, f ct f ( P 1 ) 2. A 0 Tương tự P2 là điểm cực tiểu. 30-Jan-21 TS. Nguyễn Văn Quang 109 Đại học Công nghệ - ĐHQGHN Ví dụ 2 Tại điểm dừng P 3 (0,0) : AC B 0 chưa kết luận được. Khảo sát bằng định nghĩa: ffxyf ( , ) (0,0) xyx4 4 2 2 xyy 2 Xét dấu của f trong lân cận của (0,0): 1 n Chọn dãy: (xynn , ) ,0 (0,0) n 1 1 1 n2 Khi đó: f( x , y ) 0 nn n4 n 2 n 4 11 n Chọn dãy: (xynn , ) , (0,0) nn 1 1 2 Khi đó: f( x , y ) 0 nn n4 n 4 n 4 Vậy hàm không đạt cực trị tại (0,0). 30-Jan-21 TS. Nguyễn Văn Quang 110 Đại học Công nghệ - ĐHQGHN Ví dụ 30-Jan-21 TS. Nguyễn Văn Quang 111 Đại học Công nghệ - ĐHQGHN Ví dụ Khảo sát cực trị của hàm: f ( x , y ) 1 x 22 y x fx 0 22 xy 1) Tìm điểm dừng: Không có điểm dừng. y f y 0 22 xy Dùng định nghĩa ta thấy đạo hàm riêng theo x, theo y tại (0,0) không tồn tại. Do đó (0,0) là điểm tới hạn, nhưng không phải là điểm dừng. f(0,0) f (,) x y f (0,0) x22 y 0 f(0,0) 0 ( x , y ) (0,0). Suy ra (0,0) là điểm cực tiểu. 30-Jan-21 TS. Nguyễn Văn Quang 112 Đại học Công nghệ - ĐHQGHN Ví dụ Khảo sát cực trị của ( , ) = | | + 2 tại điểm (0,0). Không tồn tại f x (0,0) Điểm (0,0) không là điểm dừng. Điểm (0,0) là điểm tới hạn. f(,) x y f (0,0)|| x y2 0 Do đó (0,0) là điểm cực tiểu. 30-Jan-21 TS. Nguyễn Văn Quang 113 Đại học Công nghệ - ĐHQGHN Cực trị có điều kiện Đồ thị của f ( x , y ) 2 x 2 y là mặt phẳng. Không có cực trị ∀( , ) ∈ 푅2. Xét điều kiện: xy 22 1 Khảo sát cực trị trên đường Ellipse là giao của mặt phẳng và mặt trụ. Tồn tại cực trị có điều kiện. 30-Jan-21 TS. Nguyễn Văn Quang 114 Đại học Công nghệ - ĐHQGHN Cực trị có điều kiện Hàm số: z x 22 2 y Xét điều kiện: xy 22 1 Khảo sát cực trị trên đường cong C là giao của mặt cong z(x,y) và mặt trụ. Tồn tại cực trị có điều kiện. 30-Jan-21 TS. Nguyễn Văn Quang 115 Đại học Công nghệ - ĐHQGHN Cực trị có điều kiện Định nghĩa Hàm = ( , ) đạt cực đại tại 0( 0, 0) với điều kiện 휑 , = 0 nếu tồn tại một lân cận của 0, 0 : , ≤ ( 0, 0), với mọi ( , ) thuộc lân cận đó và thỏa mãn điều kiện 휑 , = 0. Tức là: BMr(0 ,): MBMrfM ( 0 ,):() fM ( 0 );()0 M Định nghĩa tương tự cho cực tiểu có điều kiện. 30-Jan-21 TS. Nguyễn Văn Quang 116 Đại học Công nghệ - ĐHQGHN Cực trị có điều kiện Điểm M 0 (,) x 0 y 0 được gọi là điểm kỳ dị của đường cong (xy , ) 0 nếu xy ( MM 00 ) 0; ( ) 0 Định lý (điều kiện cần của cực trị có điều kiện) Điểm thỏa các điều kiện: 1) 0 không là điểm kỳ dị của đường cong ( xy , ) 0 2) f ( x , y ), ( x , y ) và các đạo hàm riêng cấp 1 liên tục trong lân cận của 0 3) Hàm ( , ) với điều kiện ( xy , ) 0 đạt cực trị tại 0 fxx ( M00 ) ( M ) 0 Khi đó tồn tại một số thỏa mãn: fyy ( M00 ) ( M ) 0 (M 0 ) 0 30-Jan-21 TS. Nguyễn Văn Quang 117 Đại học Công nghệ - ĐHQGHN Cực trị có điều kiện Số được gọi là nhân tử Lagrange. Hàm L (,)(,)(,) x y f x y x y được gọi là hàm Lagrange. Định lý (điều kiện đủ của cực trị có điều kiện) Giả sử f ( x , y ), ( x , y ) khả vi liên tục đến cấp 2 trong lân cận của M 0 Trong lân cận của thỏa mãn các điều kiện trong định lý điều kiện cần. 2 d L( M 0 ) 0 M0 là điểm cực tiểu có điều kiện. 2 d L( M 0 ) 0 là điểm cực đại có điều kiện. 2 d L() M 0 không xác định dấu không là điểm cực trị. 30-Jan-21 TS. Nguyễn Văn Quang 118 Đại học Công nghệ - ĐHQGHN Sơ đồ khảo sát cực trị của = ( , ) với điều kiện (xy , ) 0 1) Lập hàm Lagrange: L (,)(,)(,) x y f x y x y Lx ( x , y ) 0 P1( x 1 , y 1 ), 1 Tìm điểm dừng của 퐿( , ): L y ( x , y ) 0 P2( x 2 , y 2 ), 2 (xy , ) 0 2) Tính tất cả các đạo hàm riêng cấp hai LLL xx ,,. xy yy 3) Khảo sát từng điểm dừng. 2 2 2 P1( x 1 , y 1 ), 1 : d L( P1 ) Lxx ( P 1 ) dx 2 L xy ( P 1 ) dxdy L yy ( P 1 ) dy Dựa vào định lý điều kiện đủ để kết luận. Tương tự khảo sát các điểm dừng còn lại. 30-Jan-21 TS. Nguyễn Văn Quang 119 Đại học Công nghệ - ĐHQGHN Chú ý: 2 1) Để khảo sát d L () P 1 ta có thể sử dụng điều kiện: (xy , ) 0 d ( x , y ) 0 dP (1 ) 0 xy (P11 ) dx ( P ) dy 0. Từ đây ta có theo (hoặc theo ). 2 2 2 Thay vào biểu thức của d L () P 1 , ta có một hàm theo (hoặc ). 2) Trong bài toán cực trị có điều kiện: và khác 0. 3) Nếu từ 휑 , = 0 → = hoặc = ( ), khi đó hàm ( , ) sẽ thành hàm 1 biến theo hoặc . Khảo sát cực trị của hàm 1 biến này. 30-Jan-21 TS. Nguyễn Văn Quang 120 Đại học Công nghệ - ĐHQGHN Tìm cực trị của hàm f ( x , y ) 2 x 22 12 xy y với điều kiện xy 22 4 25 1) Hàm Lagrange: L (,)2 x y x 2 12 xy y 2 ( x 2 4 y 2 25) Lx 4 x 12 y 2 x 0 2 :PP (3, 2), ( 3,2) 1 1 2 L y 12 x 2 y 8 y 0 17 3 3 :PP (4, ), ( 4, ) 22 24 3 2 4 2 (x , y ) x 4 y 25 0 2) Tìm đạo hàm riêng cấp 2: LLL xx 4 2 , xy 12, yy 2 8 3) Khảo sát từng điểm dừng: P 11 (3, 2), 2: 2 2 2 22 d L( P1 ) Lxx ( P 1 ) dx 2 L xy ( P 1 ) dxdy L yy ( P 1 ) dy 8dx 24 dxdy 18 dy 2(2dx 3 dy )2 0 → P1 là điểm cực tiểu có điều kiện. 30-Jan-21 TS. Nguyễn Văn Quang 121 Đại học Công nghệ - ĐHQGHN Tìm cực trị của hàm f ( x , y ) 6 5 x 4 y với điều kiện xy 22 9 1) Hàm Lagrange: L ( x , y ) 6 5 x 4 y ( x22 y 9) Lx 5 2 0 x P (5, 4), 1/ 2 11 Ly y 4 2 0 P22( 5,4), 1/ 2 22 (x , y ) x y 9 0 2) Tìm đạo hàm riêng cấp 2: LLL xx 2 , xy 0, yy 2 3) Khảo sát từng điểm dừng: P 11 (5, 4), 1/ 2: 2 2 2 22 d L( P1 ) Lxx ( P 1 ) dx 2 L xy ( P 1 ) dxdy L yy ( P 1 ) dy dx dy 5 từ điều kiện: dP ( ) 0 10dx 8 dy 0 dy dx 1 4 2 2 2 59 2 d L( P1 ) dx dx dx 0 → P1 là điểm cực đại có điều kiện. 4 16 30-Jan-21 TS. Nguyễn Văn Quang 122 Đại học Công nghệ - ĐHQGHN Giá trị lớn nhất, nhỏ nhất Định nghĩa Số được gọi là giá trị lớn nhất của hàm f trên một tập đóng và bị chặn D, nếu M D :() f M a và M 00 D :() f M a Tương tự ta có định nghĩa giá trị nhỏ nhất. Nhắc lại: Để tìm giá trị lớn nhất, nhỏ nhất của = ( ) trên [ , ]: 1) Tìm điểm tới hạn thuộc ( , ): xx12, ,... Loại các điểm không thuộc ( , ). Tính giá trị của tại những điểm còn lại. 2) Tính giá trị ( ), ( ). 3) So sánh giá trị của ở bước 1) và bước 2). Kết luận. 30-Jan-21 TS. Nguyễn Văn Quang 123 Đại học Công nghệ - ĐHQGHN Giá trị lớn nhất, nhỏ nhất Định lý Weierstrass Hàm nhiều biến f liên tục trên tập đóng, bị chặn D thì đạt giá trị lớn nhất và giá trị nhỏ nhất tại các điểm tới hạn trong D, hoặc tại các điểm biên của D. Để tìm giá trị lớn nhất, nhỏ nhất của hàm nhiều biến f trên D: 1) Tìm trong D (các điểm trong của D) (bài toán tìm cực trị không điều kiện) Tìm điểm tới hạn của f : PP12, ,... Loại các điểm không là điểm trong của D. Tính giá trị của f tại những điểm còn lại. 2) Tìm cực trị của f trên biên D (bài toán tìm cực trị có điều kiện). 3) So sánh giá trị của f ở bước 1) và bước 2). Kết luận. 30-Jan-21 TS. Nguyễn Văn Quang 124 Đại học Công nghệ - ĐHQGHN Giá trị lớn nhất, nhỏ nhất Chú ý: 1) Tìm trên biên D: giả sử biên D cho bởi phương trình (xy , ) 0 Tìm trên biên D tức là tìm cực trị của ( , ) với điều kiện (xy , ) 0 Lập hàm Lagrange: L(,)(,).(,) x y f x y x y Lx ( x , y ) 0 Q1(,) x 1 y 1 Tìm điểm dừng của 퐿: L y ( x , y ) 0 Q2(,) x 2 y 2 (xy , ) 0 Tính giá trị của tại các điểm 푄1, 푄2, 30-Jan-21 TS. Nguyễn Văn Quang 125 Đại học Công nghệ - ĐHQGHN Giá trị lớn nhất, nhỏ nhất Chú ý: 2) Trường hợp đặc biệt, biên của D là những đoạn thẳng. Tìm trên từng đoạn thẳng. Giả sử tìm trên đoạn AB có phương trình: ac ax by c ( b 0) yx bb Thay vào hàm ( , ) ta có hàm một biến x, tìm GTLN, GTNN của hàm này. 30-Jan-21 TS. Nguyễn Văn Quang 126 Đại học Công nghệ - ĐHQGHN Giá trị lớn nhất, nhỏ nhất Tìm giá trị lớn nhất, giá trị nhỏ nhất của f ( x , y ) ( x 6) 22 ( y 8) trên miền D: xy 22 25 fxx 2( 6) 0 1) Tìm trong D: P (6, 8) D 1 fyy 2( 8) 0 2) Tìm trên biên của D: ( x , y ) x 22 y 25 0 Lập hàm Lagrange: L ( x , y ) ( x 6) 2 ( y 8) 2 ( x 2 y 2 25) 30-Jan-21 TS. Nguyễn Văn Quang 127 Đại học Công nghệ - ĐHQGHN Giá trị lớn nhất, nhỏ nhất Lx 2( x 6) 2 x 0 Tìm điểm dừng của L: L y 2( y 8) 2 y 0 QQ 12 (3, 4); ( 3,4) 22 xy 25 f( Q1 ) f (3, 4) 25 f( Q2 ) f ( 3,4) 225 3) So sánh giá trị của f ở bước 1) và bước 2). Kết luận. Giá trị lớn nhất là 225 đạt tại (-3,4). Giá trị nhỏ nhất là 25 đạt tại (3,-4). 30-Jan-21 TS. Nguyễn Văn Quang 128 Đại học Công nghệ - ĐHQGHN Giá trị lớn nhất, nhỏ nhất Tìm giá trị lớn nhất, giá trị nhỏ nhất của f (,) x y x 22 xy y trên miền D: | xy | | | 1 A(0,1) D( 1,0) B(1,0) C(0, 1) f 20 x y 1) Tìm trong D: x P (0,0) D fP() 0 1 1 fy x 20 y 30-Jan-21 TS. Nguyễn Văn Quang 129 Đại học Công nghệ - ĐHQGHN Giá trị lớn nhất, nhỏ nhất 2) Tìm trên biên của D. Có 4 cạnh. Tìm trên từng cạnh một. Trên AB: phương trình AB là: y 1 x , x [0,1] f x2 x(1 x ) (1 x ) 2 3 x 2 3 x 1 Tìm giá trị lớn nhất, nhỏ nhất của hàm một biến trên [0,1]. 1 f 6 x 3 0 x [0,1] 2 11 Trên AB có 3 điểm cần xét: A(0,1), B(1,0) và Q1 , 22 1 Tính giá trị của f tại 3 điểm này: f();(); A 1 f B 1 f( Q ) 1 4 Tương tự tìm trên 3 cạnh còn lại. 3) So sánh, kết luận: GTLN: 1; GTNN: 0. 30-Jan-21 TS. Nguyễn Văn Quang 130 Đại học Công nghệ - ĐHQGHN Giá trị lớn nhất, nhỏ nhất Tìm giá trị lớn nhất, giá trị nhỏ nhất của f (,) x y x 22 y trên miền D: x 22 y 2 x fx 20 1) Tìm trong D: x P (0,0) loại vì không là điểm trong của D. 1 fyy 20 30-Jan-21 TS. Nguyễn Văn Quang 131 Đại học Công nghệ - ĐHQGHN Giá trị lớn nhất, nhỏ nhất 2) Tìm trên biên D: ( x , y ) x 22 y 2 x 0 y22 2 x x Tìm giá trị lớn nhất, nhỏ nhất của hàm một biến: f x2 (2 x x 2 ) 2 x 2 2 x trên [0,2] 1 1 1 f 4 x 2 0 x f ; f(0) 0 ; f (2) 4 2 2 2 1 3) So sánh, kết luận: Giá trị lớn nhất là 4 ; giá trị nhỏ nhất là 2 Chú ý: có thể lập hàm Lagrange. 30-Jan-21 TS. Nguyễn Văn Quang 132 Đại học Công nghệ - ĐHQGHN 30-Jan-21 TS. Nguyễn Văn Quang 133 Đại học Công nghệ - ĐHQGHN 30-Jan-21 TS. Nguyễn Văn Quang 134 Đại học Công nghệ - ĐHQGHN 30-Jan-21 TS. Nguyễn Văn Quang 135 Đại học Công nghệ - ĐHQGHN 30-Jan-21 TS. Nguyễn Văn Quang 136 Đại học Công nghệ - ĐHQGHN
File đính kèm:
 bai_giang_giai_tich_ii_chuong_2_dao_ham_vi_phan_nguyen_van_q.pdf
bai_giang_giai_tich_ii_chuong_2_dao_ham_vi_phan_nguyen_van_q.pdf

