Bài giảng Đại số tuyến tính - Chương I: Logic. Tập hợp. Ánh xạ. Số phức - Nguyễn Hải Sơn

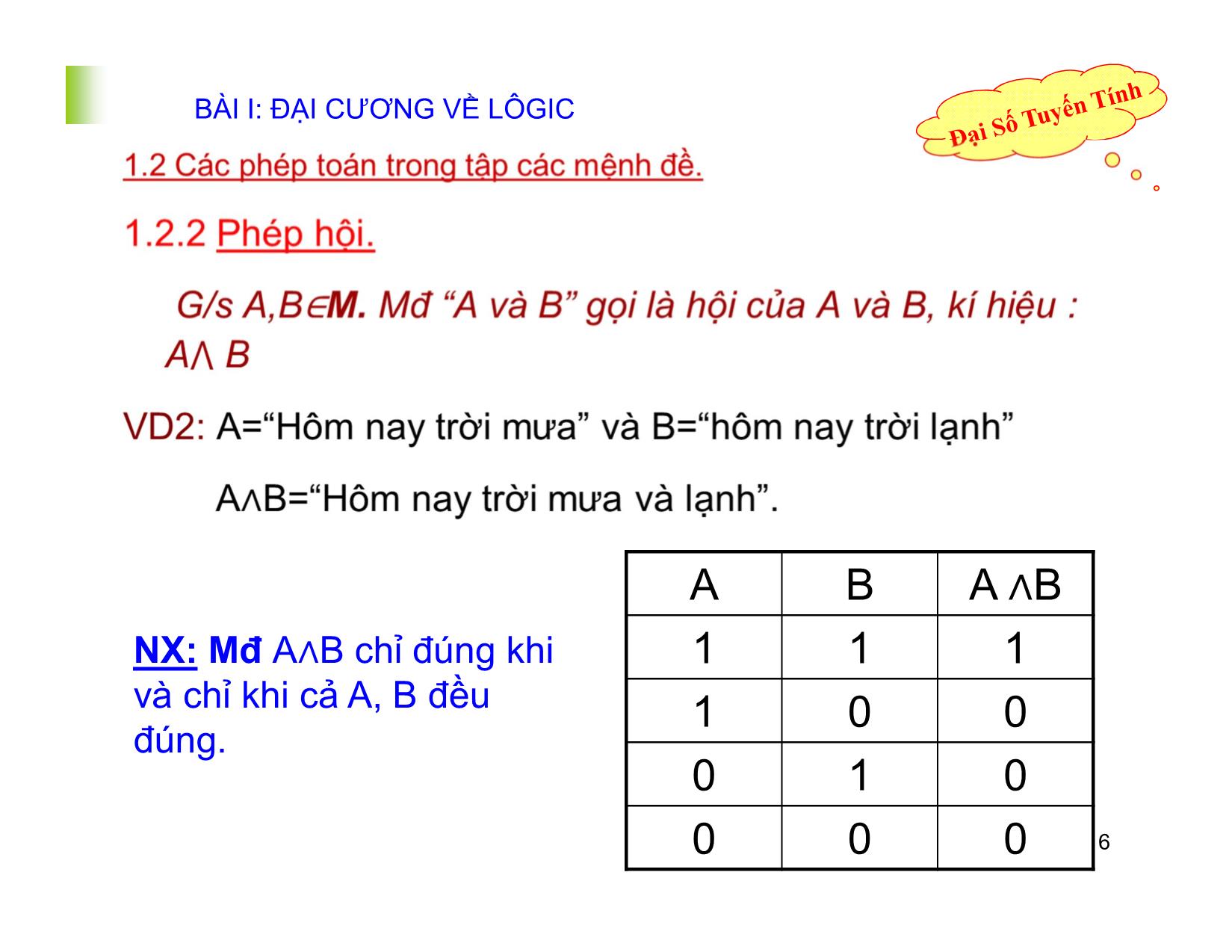
)  (  ) \ ( AB  ) bABCABC ) ( \ ) \ \ (  )
Lời giải: b) ( A \ B ) \ C A \ ( B  C )
Cách 1: Phương pháp phần tử. 
 35
BÀI II: SƠ LƯỢC VỀ LÍ THUYẾT TẬP HỢP
 b) ( A \ B ) \ C A \ ( B  C )
Cách 2: Phương pháp biến đổi tương đương.
 36
BÀI II: SƠ LƯỢC VỀ LÍ THUYẾT TẬP HỢP
2.4 Tích Descartes (Đề các) 
 2.4.1 Hai bộ số bằng nhau
 m n
 (a1 ; a 2 ;...; am ) ( b 1 ; b 2 ;...; b n ) 
 ai b i ;  i 1, n
 2.4.2. Đ/n: Tích Descartes của các tập hợp AAA 1 , 2 ,..., n 
là một tập hợp n
 CAAAA 1 2 ... n  i
 i 1
xác định như sau:
 (i ) C  khi  i : Ai 
 (ii ) C=A1 khi n 1
 (iiiC ) {( aa ; ;...; a ) | a Ai ; 1, n }
 1 2 n i i 37
BÀI II: SƠ LƯỢC VỀ LÍ THUYẾT TẬP HỢP
2.4 Tích Descartes (Đề các) 
 n
*Chú ý: Khi AAAA 1 2 ... n thì viết CA 
VD: A={a;b}, B={1;2;3}. Xác định 
 a) ABBAA ; ; 2
 b) Phần tử (a;2;b) thuộc tập hợp nào? 
 c) Số phần tử của AxBxAxB. 
Lời giải: 
 38
MỘT SỐ ĐỀ THI
Bài 1. Với A, B, C là các tập hợp bất kì, CMR
 (i) (\)\\() ABCABC 
 (ii) ABCABAC \(\)(\)()  
Bài 2. Cho các tập hợp A, B, C thỏa mãn 
 ()()ABAC   và ()()ABAC  
 CMR: BC
 (Đề 3-K51)
 39
 BÀI III: ÁNH XẠ
3.1 Định nghĩa.
a. Đ/n: Cho X,Y≠  . Ánh xạ f từ X đến Y là một quy tắc 
 cho tương ứng mỗi phần tử x của X với một và chỉ một
 phần tử y của Y.
 f: X Y
 x y f ( x )
 y=f(x): ảnh của x qua ánh xạ f
 X: tập nguồn Y: tập đích
 VD1: Ánh xạ đồng nhất của tập X: IXXX : 
 x x
 VD2: X: tập người, Y: tập tên người. Ánh xạ f từ X đến Y 
 cho mỗi người với 1 tên tương ứng
 40
 BÀI III: ÁNH XẠ
3.1 Định nghĩa.
b. Tập ảnh và tập nghịch ảnh. 
Cho ánh xạ: 
 f: X Y và AXBY, 
 x y f ( x )
 - Ảnh của tập A: f( A ) { f ( x ) | x A }
 Đặc biệt, f(X)=Imf gọi là ảnh của X qua f .
 - Tập nghịch ảnh của B: f 1( B ) { x X | f ( x ) B }
 2x 3
VD1. Cho ánh xạ , f : \{ 1} , f ( x ) 
 Xác định x 1
 a) f ({0;2}), f 1 (0), f 1 ({0;7})
 1
 b) f (( 1;0]), f ([4;7)) (Đề1- 08/2010) 41
 BÀI III: ÁNH XẠ
NX: (i ) y f ( A )  x A , y f ( x )
 (ii ) x f 1 ( B ) f ( x ) B
VD2. CM các tính chất của ảnh và nghịch ảnh của ánh xạ 
 (i) f(A B) f(A)  f(B);A,B  X
 (ii) f 1 (A B) f 1 (A)  f 1 (B);A,B  Y
 42
BÀI III: ÁNH XẠ
3.2 Đơn ánh, toàn ánh, song ánh.
Đ/n: Cho ánh xạ f: X→Y 
(if ) : ®¬n ¸nh  xxXfxfx1 , 2 ,( ( 1 ) ( 2 )) ( xx 1 2 )
 x1 , x 2 X ,( x 1 x 2 ) ( f ( x 1 ) f ( x 2 ))
 y Y , pt f ( x ) y có kh«ng qu¸ 1 nghiÖm 
(ii ) f : toµn ¸nh f ( X ) Y 
 y Y ,  x X , y f ( x )
 y Y , pt f ( x ) y lu«n có nghiÖm. 
 f : ®¬n ¸nh
(iii ) f : song ¸nh 
 f : toµn ¸nh
 43
BÀI III: ÁNH XẠ
3.2 Đơn ánh, toàn ánh, song ánh.
VD1. Phủ định các mệnh đề trên và chỉ ra: để chứng minh f
 không là đơn ánh (toàn ánh, song ánh), ta phải làm gì.
VD2. Xét xem trong các ánh xạ sau có là đơn ánh, toàn 
 ánh hay song ánh không 
 a) f : c) f : 
 x f ( x ) x2 x f ( x ) x2
 b) f : d) f : 
 x f ( x ) x2 x f ( x ) x2
 44
BÀI III: ÁNH XẠ
3.2 Tích của hai ánh xạ.
Đ/n: Cho hai ánh xạ f: X→Y và g: Y→Z. 
 Ánh xạ h : X →Z xác định bởi h(x)=g(f(x)) với mọi x∈X 
 gọi là ánh xạ tích (ánh xạ hợp thành) của f và g , kí 
 hiệu: gf . 
 f g
 X Y Z
 g ◦f
 VD. Cho các ánh xạ 
 f : \ {1} g : 
 x x g ( x ) x2
 x f ( x ) 
 x 1
 45
 Xác định các ánh xạ g ◦f và f ◦ g (nếu có)
BÀI III: ÁNH XẠ
 3.3 Ánh xạ ngược.
 Đ/n. Cho song ánh f: X→Y. Khi đó, với mỗi y của Y đều 
 tồn tại duy nhất một x của X để f(x)=y hay f 1 () y x . 
 Như vậy, ta có ánh xạ: 
 f 1 : Y X
 y x f 1 ( y )
 Ánh xạ này cũng là một song ánh và gọi là ánh xạ ngược 
 của f .
 VD1 Xác định ánh xạ ngược của các ánh xạ sau: 
 a) f : b) g : \ {0} \ {0}
 3 1
 x f ( x ) x 1 x g ( x ) 
 x3
 46
MỘT SỐ ĐỀ THI
 x 2
Bài 1.Cho ánh xạ ,f : \{ 1} , f ( x ) 
 x 1
 Xác định f((3;5]), f 1 ([2;7))
 (Đê 2- hè 2010)
Bài 2. Cho ánh xạ f: , f ( z ) z6 3 z 3
 Tìm f 1( 4)
 (Đề 3-K51)
Bài 3. Cho ánh xạ f: , f ( z ) 3 z4 5 iz 2
 1) f có là đơn ánh ? toàn ánh không? Vì sao
 2) Cho B={-2}. Tìm f 1() B
 (Đề 3-K53)
 47
 MỘT SỐ ĐỀ THI
 Bài 4.Cho ánh xạ f: 2 2 , f ( x , y ) ( x 2 y ,2 x y )
 a) CM f là một song ánh. 
 b) Cho tập A {(x;y) 2 |x 2 +y 2 =45} . Tìm nghịch ảnh f 1() A
 (Đề 3- K55)
Bài 5. Như câu 4 với f( x , y ) (3 x y ; x 3 y )
 A {(x;y) 2 |x 2 +y 2 =40} (Đề 4- K55)
 Bài 6. Cho các ánh xạ f :,: X Y g Y Z có ánh xạ hợp 
 thành . Giả sử là toàn ánh và là đơn ánh. 
 g0 f: X Z f g0 f
 CMR g là đơn ánh. 
 (Đề 4- K51)
 48
 BÀI IV: SỐ PHỨC
 4.1 Phép toán hai ngôi.
 4.1.1 Khái niệm. Phép toán hai ngôi (phép toán) * trên tập 
 E là một quy luật khi tác động lên hai phần tử a và b của 
 E sẽ tạo ra một và chỉ một phần tử cũng của E.
 *: EEE 
 (a,b) a * b
VD1: Phép cộng (+) và phép nhân (.) thông thường trên
 các tập số: N, Z, Q, R, C. 
VD2: Phép giao và phép hợp trên tập các tập hợp.
?1: Phép chia là phép toán trên tập R hay không?
?2: Hãy cho biết các phép toán trên tập các mệnh đề?
 49
BÀI IV: SỐ PhỨC
4.1.2 Tính chất của phép toán.
Cho phép toán * trên tập E. 
a. Tính kết hợp: (a*b)*c=a*(b*c) với mọi a,b,c ∈E
b. Tính giao hoán: a*b=b*a với mọi a,b∈E
c. Phần tử trung hòa e: e E,  a E : a * e e * a a
d. Phần tử đối ( hay đối xứng): G/s có phần tử trung hòa e. 
 Xét phần tử a∈E, phần tử b gọi là phần tử đối của a nếu
 a*b=b*a=e
* Chú ý: - phép toán được đặt tên là phép cộng (phép 
 nhân) thì phần tử đối xứng gọi là phần tử đối (nghịch 
 đảo) và kí hiệu là –a ( a-1 )
 50
 BÀI IV: SỐ PHỨC
 VD1. Trên tập N, Z, Q xét xem phép cộng, phép nhân có 
 những tính chất gì?
 (+) Kết hợp Giao hoán Pt trung Pt đối 
 hòa xứng
 N
 Z
 Q
(.) Kết hợp Giao hoán Pt trung Pt đối 
 hòa xứng
N -
Z -
Q - 51
BÀI IV: SỐ PHỨC
VD2. Trên tập các mệnh đề, các phép hội, tuyển, kéo theo 
 có những tính chất gì?
 Kết hợp Giao hoán Pt trung Pt đối 
 hòa xứng
 ∧
 ∨
 →
VD3. Trên tập các tập hợp, các phép giao, phép hợp có 
 những tính chất gì?
 52
BÀI IV: SỐ PHỨC
4.1.3 Cấu trúc đại số
Một tập hợp được trang bị một hay nhiều phép toán với 
 các tính chất xác định gọi là một cấu trúc đại số. 
VD: nửa nhóm, nhóm, vành, trường, đại số,
 53
BÀI IV: SỐ PHỨC
 4.2 Nhóm-vành – trường. 
 4.2.1 Nhóm (Group)
 a. Đ/n. Cho tập G khác rỗng với phép toán * . Khi đó 
 (G,*) là một nhóm nếu thảo mãn 3 tiên đề: 
 ()i  xyzGxyzxyz , , : (*)* *(*)
 (ii )  eG :  xGxeexx , * * 
 ()iii  xGx ,  ' Gxx , *' xxe '* 
 e: phần tử trung hòa, x’: phần tử đối của x
 Nhóm (G,*) gọi là nhóm giao hoán (hay nhóm Abel) 
 nếu t/m: 
 (iv )  x , y G : x * y y * x
 54
55
Vào 5 tháng 6, 2002, bốn tem 
Norwegian được phát hành để kỉ 
niệm Abel 2 tháng trước 200 
năm ngày sinh của ông. Có một 
bức tượng của Abel ở Oslo. Hố 
Abel trên Mặt trăngđược đặt 
theo tên ông. Vào năm 2002, giải 
Abel đã được thiết lập để vinh 
danh ông.
Giải Abel, giải Wolf hay giải 
Fields đều được xem là “Nobel 
toán học”. Xét về danh tiếng thì 
giải Abel và Wolf không thua 
kém gì Fields, mỗi giải đều có 
một ưu thế nổi trội riêng và tất 
cả đều là vinh dự lớn của các 
nhà toán học trên thế giới. 
 56
Évariste Galois là một thiên tài toán 
học người Pháp đoản mệnh, nhưng 
các công trình toán học ông để lại là 
một đề tài rất quan trọng cho việc 
tìm nghiệm của các phương trình đa 
thức bậc cao hơn 4 thông qua việc 
xây dựng lý thuyết nhóm trừu tượng 
mà ngày nay được gọi là lý thuyết 
nhóm Galois. 
 57
 BÀI IV: SỐ PHỨC
4.2.1 Nhóm
b. Một số tính chất của nhóm.
 (i) Phần tử trung hòa e là duy nhất.
 (ii) Phần tử đối x’ là duy nhất 
 (iii) Luật giản ước: a* b a * c b c
 (iv) Pt a * x b có nghiệm duy nhất x a'* b
 VD1. (Z,+), (Q,+), (R,+), (Q*, .), (R*, .) là các nhóm Abel.
 (N,+), (Z*,.) không là một nhóm. 
 VD2. Tập các song ánh trên một tập X với phép hợp 
 thành là một nhóm. Nếu X có nhiều hơn hai phần tử thì 
 nhóm đó không giao hoán. 
 58
BÀI IV: SỐ PHỨC
 4.2 Nhóm-vành – trường. 
 4.2.2 Vành (Ring)
 a. Đ/n. Cho tập G khác rỗng với hai phép toán kí hiệu là 
 “+” và “.” . Khi đó (G,+,.) là một vành nếu thảo mãn: 
 (i) (G,+) là một nhóm giao hoán 
 (ii)Tính kết hợp của phép “.”
 (x . y ). z x .( y . z )
 (iii) Tính phân phối của phép “.” và phép “+”
 x .( y z ) x . y x . z
 (y z ). x y . x z . x
 59
 BÀI IV: SỐ PHỨC
4.2.2 Vành
 Vành (G,+,.) gọi là giao hoán nếu x, y G : x . y y . x
gọi là có đơn vị là 1 nếu phép nhân có phần tử trung hòa là 1. 
b. Ví dụ.
 VD1. (Z,+,.), (Q,+,.), (R,+,.) là các vành giao hoán có đơn 
 vị là 1.
 Z a b a b Z
 VD2. 2 { 2 | , } lµ mét vµnh
 60
BÀI IV: SỐ PHỨC
 4.2 Nhóm-vành – trường. 
 4.2.3 Trường (Field)
 a. Đ/n. Cho tập G khác rỗng với hai phép toán kí hiệu là 
 “+” và “.” . Khi đó (G,+,.) là một trường nếu thảo mãn: 
 (i ) ( G , ,.) lµ mét vµnh giao ho¸n, ®v 1
 (ii )  x G \ {0},  x ' : x . x ' 1
 b. NX. Nếu (G,+,.) là một trường thì (G\{0},.) là một nhóm
 c. VD:
 VD1: (Z,+,.) không là một trường. 
 (Q,+,.), (R,+,.) là một trường.
 VD2. Z a b a b Z
 2 { 2 | , } ko lµ mét tr­êng
 Q 2 { a b 2 | a , b Q } lµ mét tr­êng 61
 BÀI IV: SỐ PHỨC
 4.3 Số phức
 4.3.1 Xây dựng trường số phức
 Với R là trường số thực, xét tập C=RxR={(a,b)|a,b∈R}
 + Quan hệ bằng nhau trên C:
 a c
 (,)(,)a b c d 
 b d
 + Trên C trang bị hai phép toán:
 - Phép cộng “+” : (,)(,)(,)a b c d a c b d
 - Phép nhân “.” : (ab , ).( cd , ) ( ac bdad ; bc )
 (C,+,.) là một trường với phần tử không là (0;0), pt đơn vị 
 là (1;0) và phần tử nghịch đảo của (a;b) là 
 a b 
 2 2; 2 2 62
 a b a b 
BÀI IV: SỐ PHỨC
 4.3 Số phức
 4.3.1 Xây dựng trường số phức
 + Xét tập con F={(a,0)|a ∈R} của C và ánh xạ 
 f : RF 
 x ( x ,0)
 Khi đó, f là một song ánh thỏa mãn 
 f(x+y)=f(x)+f(y) và f(xy)=f(x)f(y) 
 → đồng nhất R với F ((x,0) ≡ x) 
 hay R là một trường con của C. 
 63
BÀI IV: SỐ PHỨC
 4.3 Số phức
 4.3.1 Xây dựng trường số phức
 Đặt i=(0;1), ta có 
 z (a,b) (a,0) (0,b) (a,0) (b,0)(0,1) a bi
 i2 (0,1)(0,1) ( 1,0) 1
 Dạng z=a+bi gọi là dạng chính tắc của z
 a=Re(z) gọi là phần thực của z
 b=Im(z) gọi là phần ảo của z
 2
 số i gọi là đơn vị ảo i 1
 Trong C ,pt x2 1 có nghiệm x= i
 64
Heron xứ Alexandria là người đầu tiên đề cập đến số ảo 
vào khoảng thế kỷ 1 trước công nguyên trong khi tính toán 
khối hình lượng kim tự tháp, tuy nhiên, việc nghiên cứu số 
ảo chỉ thực sự bắt đầu bởi nhà toán học người Ý Rafael 
Bombelli (1526-1572) trong cuốn sách đại số 
L'Algebra viết năm 1569. Rafael Bombelli là người đưa ra 
ký hiệu đơn vị ảo i và mô tả các tính chất của nó.
 65
BÀI IV: SỐ PHỨC
 4.3 Số phức
 4.3.2 Các phép toán ở dạng chính tắc.
 (i) (a bi) (c di) (a c) (b d)i
 (ii) (a bi)(c di) (ac bd) (ad bc)i
 a bi (a bi)(c di)
 (iii) 
 c di c2 d 2
 (iv) Cho số phức z=a+bi. 
 - Số phức liên hợp của z: z a bi
 - Môđun của z: z a2 b 2
 2
 NX: z z.z
 66
 BÀI IV: SỐ PHỨC
(v) Các tính chất. 
 z1 z 2 z 2 z 1 ; z 1 z 2 z 2 z 1
 (z12 z) z 31 z (z 23 z); ( zz)z 123123 z(zz)
 z1 (z 2 z 3 ) z 1 z 2 z 1 z 3
 z1 z 2 z 1 z 2 ; z 1 z 2 z 1 .z 2
 z1 z 2 z 1 . z 2 ; z 1 z 2 z 1 z 2
 1 2i 1 3
 VD1. Tính A 
 4 3i 2i 4
 VD2. Cho |z1|=1. CMR với mọi z2 ≠ z1 ta có: 
 z z
 1 2 1 (K50-lần 2)
 1 z1 z 2
 67
 BÀI IV: SỐ PHỨC
 4.3.3 Dạng lượng giác của số phức
 a. Mặt phẳng phức.
z a bi  1 1 (a;b)  1 1 M(a;b) Oxy
 Mỗi số phức sẽ được biểu diễn bởi 1 điểm 
 nằm trên mặt phẳng Oxy và một điểm trên 
 mp Oxy biểu diễn một số phức. 
 Do đó, mp Oxy gọi là mp phức
 Ox: trục thực
 Oy: trục ảo 
 68
 BÀI IV: SỐ PHỨC
 4.3.3 Dạng lượng giác của số phức
 b. Dạng lượng giác của số phức
Cho số phức z=a+bi được biểu diễn 
bởi điểm M(a;b). 
r OM z a2 b 2 : môđun của z
  
 Ox;OM : argument của z
k/h: Arg(z) ( k2 )
 a b
 Khi đó cos , sin 
 a2 b 2 a 2 b 2
 z r(cos isin )
 69
BÀI IV: SỐ PHỨC
4.3.3 Dạng lượng giác của số phức
 z a bi  z r(cos isin )
 a b
 rz a2 b,cos 2 ,sin 
 a2 b 2 a 2 b 2
 VD1: Viết dạng lượng giác của các số phức sau:
 a)A 3i b)B22i 
 c) C 2 d) D 5
 e) E 2i f) F 3i
 70
BÀI IV: SỐ PHỨC
4.3.4 Các phép toán ở dạng lượng giác
 (i) Phép nhân và phép chia
 r(c1os 1 isin 1 )r(c 2 os 2 isin 2 ) 
 =(rr)cos(1 2 1 2 ) isin( 1 2 )
 -Khi r2≠0, ta có: 
 r1 (cos 1 isin 1 ) r 1
 cos( 1 2 ) isin( 1 2 )
 r2 (cos 2 isin 2 ) r 2
 5 5 
VD1: Cho z1 6cos isin ,z 2 4cos isin 
 12 12 6 6 
 z1
 Tính z1 .z 2 vµ 
 z2
 71
BÀI IV: SỐ PHỨC
•Chú ý: Nếu z r(cos isin ) thì 
 z r(cos( ) isin( ))
 1
 z 1 (cos( ) isin( ))
 r
(ii) Phép lũy thừa
 n n
 r(cos isin ) r cos(n ) isin(n ) (n )
 Công thức Moivre (r=1)
 (cos isin )n cos(n ) isin(n )
VD1: Tính A ( 3 i)2011
VD2: Biểu diễn sin(5x) và cos(5x) qua sinx và cosx? 
 72
BÀI IV: SỐ PHỨC
(iii) Phép khai căn
a. ĐN1: Căn bậc n của số phức z là các số phức z0 sao cho
 n
 z0 z
 Tập các căn bậc n của z kí hiệu là n z
 VD1. 4 { 2}, 1 { i }, 3 8{2,1i3} 
b. Công thức
 n r(cos isin )
 n k2 k2 
 zk rcos isin ,k0,n1 
 n n n n 
*NX: Nếu z≠0 thì n z n
 73
BÀI IV: SỐ PHỨC
 n r(cos isin )
 n k2 k2 
 zk rcos isin ,k0,n1 
 n n n n 
VD1: Tính 3 8 cos isin 
 4 4 
VD2: Tính 3 8
VD3: Tính 1 i
 74
BÀI IV: SỐ PHỨC
4.3.5 Giải phương trình bậc hai trên trường số phức
 (Tự đọc)
 ax2 bx c 0, a,b,c 
Cách giải: - Tính b2 4ac
 - Tìm z0 một căn bậc 2 của Δ
 b z
 -Nghiệm z 0
 1,2 2a
VD1: Giải các phương trình phức
 a) z2 4iz 5 0 
 b) z2 (3 i)z 14 5i 0
 c) z6 7z 3 8 0
 75
BÀI IV: SỐ PHỨC
4.3.6 Đa thức
Đ/n1. Đa thức với hệ số trên trường số F, có dạng 
 2 n
 P(x)n a 0 ax 1 ax 2 ... ax, n (a i F,  i 0,n)
 Nếu an ≠0 thì ta nói đa thức có bậc n và k/h: degPn(x)=n 
VD1: deg( x3 2x 1) 3
ĐL1. (D’Alember) Mọi đa thực có bậc dương đều có ít nhất 
một nghiệm thực hoặc phức. 
ĐL2 Mọi đa thức bậc n dương có đúng n nghiệm thực hoặc 
phức (đơn hoặc bội).
ĐL3 Mọi đa thức khác không bậc không lớn hơn n (n>0) 
không thể có quá n nghiệm thực hoặc phức. 
 76
BÀI IV: SỐ PHỨC
4.3.7 Phân tích đa thức với hệ số thực ra thừa số.
Xét đa thức 
 2 n
 P(x) a0 ax 1 ax 2 ... ax, n (a i ,  i 0,n)
ĐL1. Nếu z là một nghiệm của P(x) thì z cũng là nghiệm 
của P(x).
ĐL2 Mọi đa thức bậc n dương, với hệ số thực đều có thể 
phân tích thành tích các đa thức bậc nhất và bậc hai với biệt 
thức âm. 
VD1. Phân tích đa thức (x2-x+3)2+3 thành tích của 2 đa 
thức bậc 2 với hệ số thực. (Đề thi K55)
VD2.Cho đa thức f(z)=z4-6z3+17z2-24z+52
 a) Tính f(2i)
 b) Giải phương trình f(z)=0 (Đề thi K53) 77
MỘT SỐ ĐỀ THI
Câu 1. (Đề K49) Viết các nghiệm phức của phương trình 
sau dưới dạng chính tắc: 
 (i) z6 (1 i ) 28 0 (ii) z 4 (1 i 3) 21 0
 (iii) z5 9 z 0 (iv) z 5 16 z
Câu 2. Tìm các nghiệm phức của phương trình
(i) z6 i 3 z 3 1 i 3 0 (Đề1- 8/2010)
(ii) z2 (4 i ) z 5 i 0 
(iii) z8 7 z 4 8 0 (Đề 4-K51)
 6 1
(iv) z 2 (Đề 4-K50)
 z
 78
 MỘT SỐ ĐỀ THI
Câu 3. Phân tích đa thức (x2+x+3)2+3 thành tích của 2 đa 
thức bậc 2 với hệ số thực. (Đề thi K55)
Câu 4.Cho đa thức f(z)=z4-6z3+17z2-24z+52
 a) Tính f(2i)
 b) Giải phương trình f(z)=0 (Đề thi K53) 
 Câu 5. Cho ánh xạ f: , f ( z ) 3 z4 5 iz 2
 1) f có là đơn ánh ? toàn ánh không? Vì sao
 2) Cho B={-2}. Tìm f 1() B
 (Đề 3-K53)
 79