A rank-deficient and sparse penalized optimization model for compressive indoor radar target localization
We introduce a low-Rank and sparse penalized optimization model for solving the problem of radar imaging of indoor targets in the presence of strong wall clutter from compressed data measurements. Compressive through-wall radar imaging (TWRI) accelerates data collection and reduces operation cost, but incomplete radar data makes wall clutter mitigation and target image reconstruction become more challenging. This paper aims to tackle these difficulties by formulating the task of wall clutter suppression and target image formation as a penalized minimization problem with low-rank and sparse regularizers. The former penalty is used to model the low-dimensional attribute of the wall reflections and the later regularizer is used to represent the image of the behind-the-wall targets. We develop an iterative algorithm based on the forward-backward proximal gradient technique to solve the regularized minimization problem, which removes wall interferences and forms an indoor target image simultaneously. The effectiveness of the proposed approach is validated using extensive experiments on both simulated and real radar data

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5
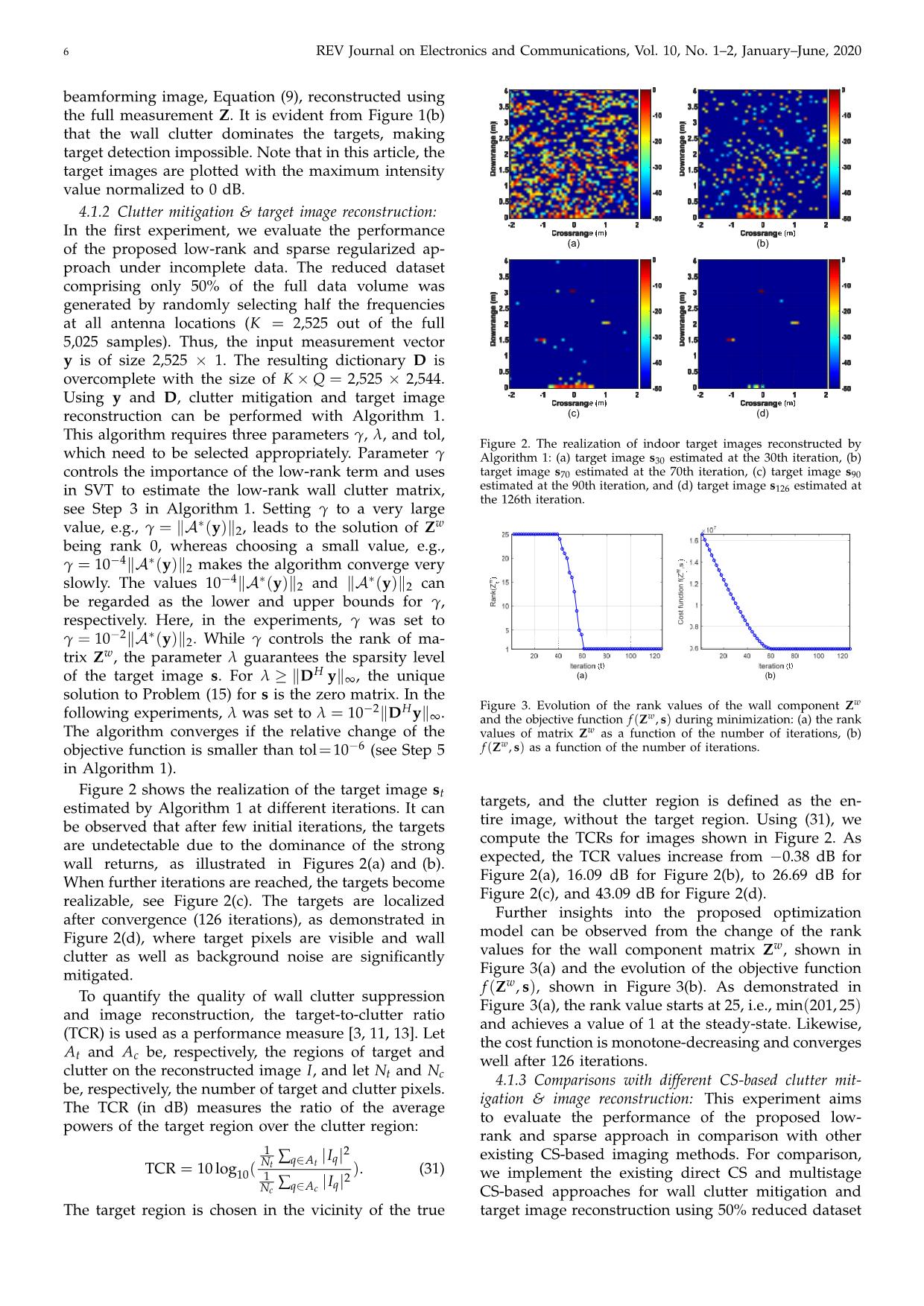
Trang 6
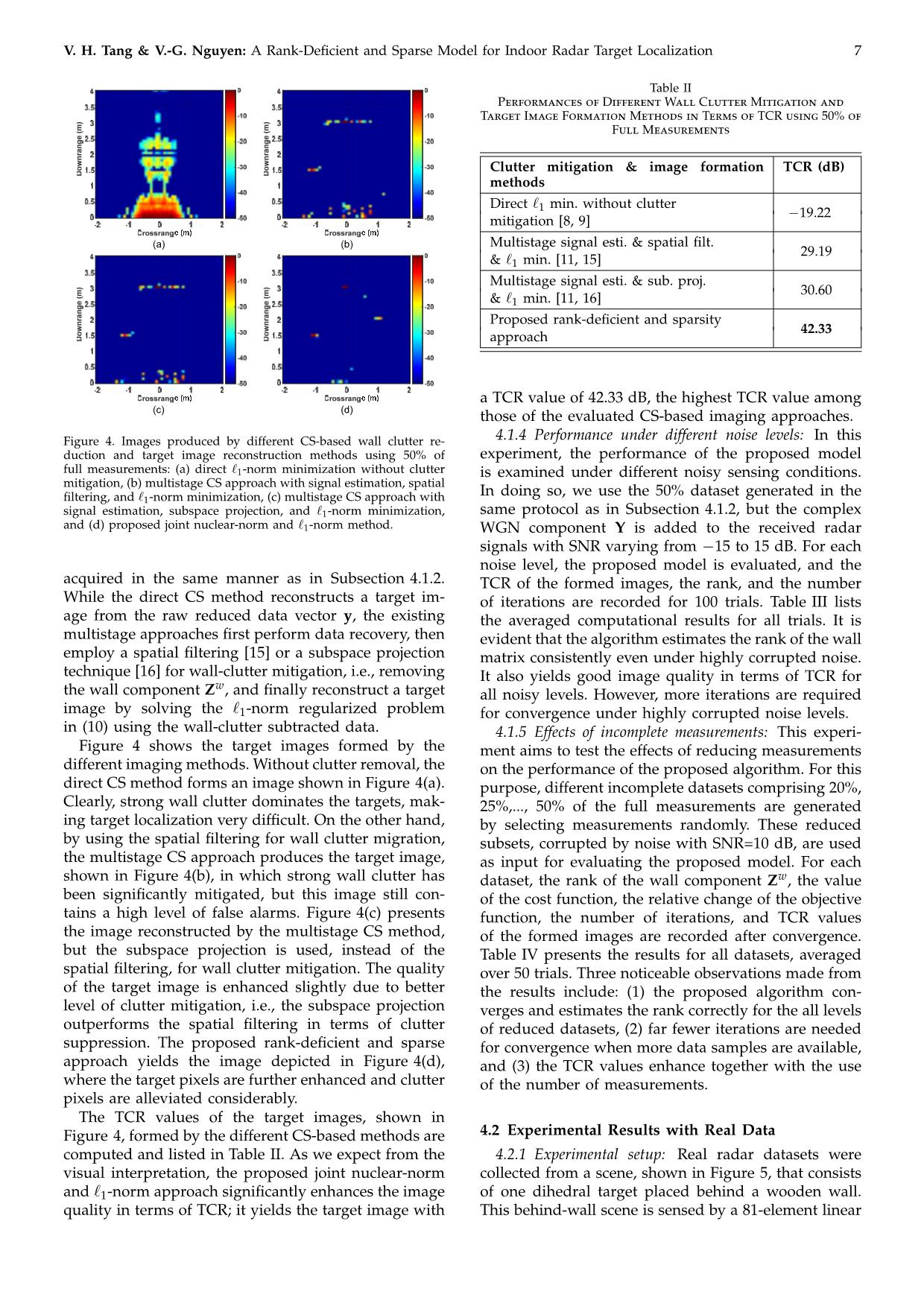
Trang 7
Trang 8
Trang 9

Trang 10
Tóm tắt nội dung tài liệu: A rank-deficient and sparse penalized optimization model for compressive indoor radar target localization

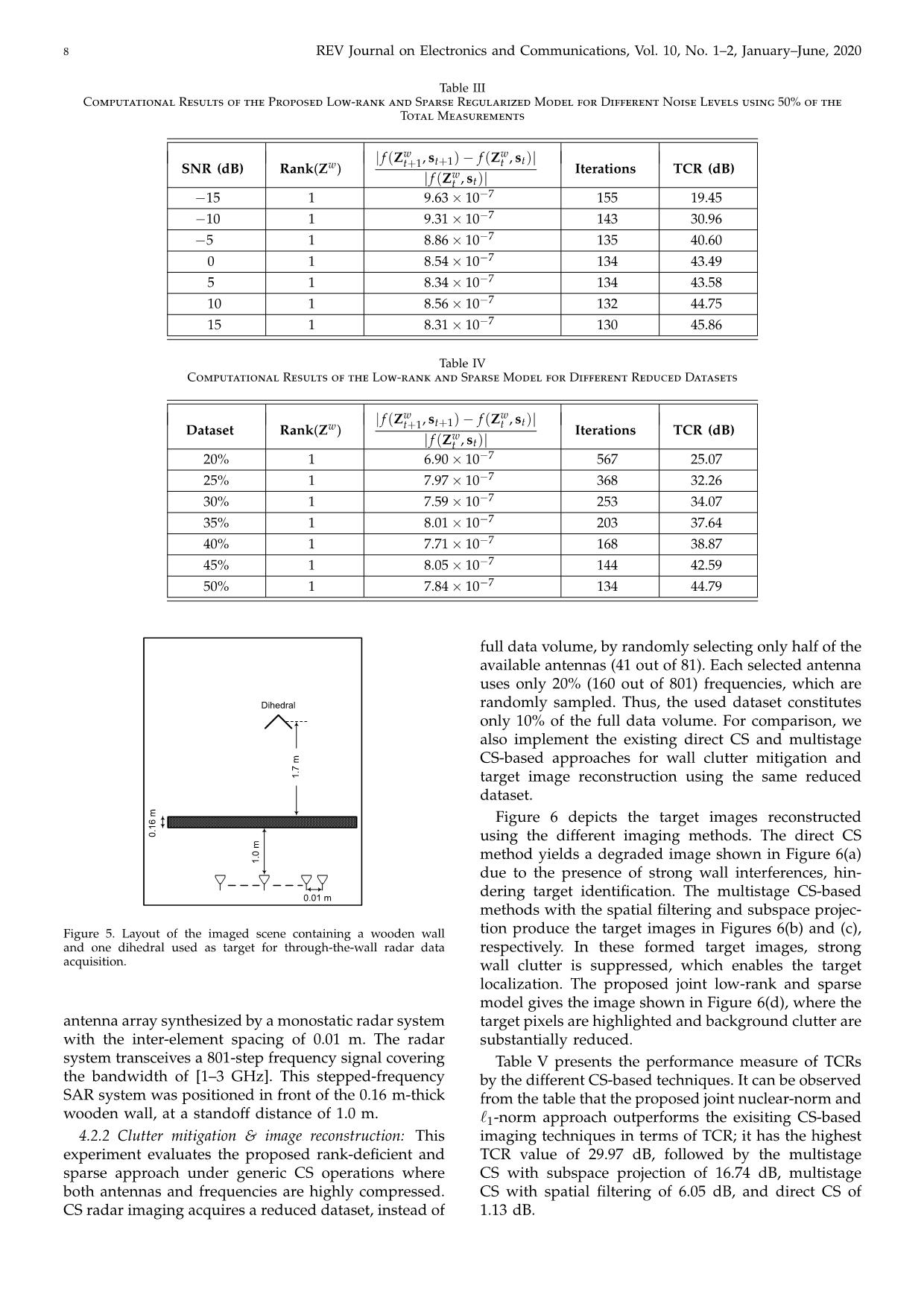
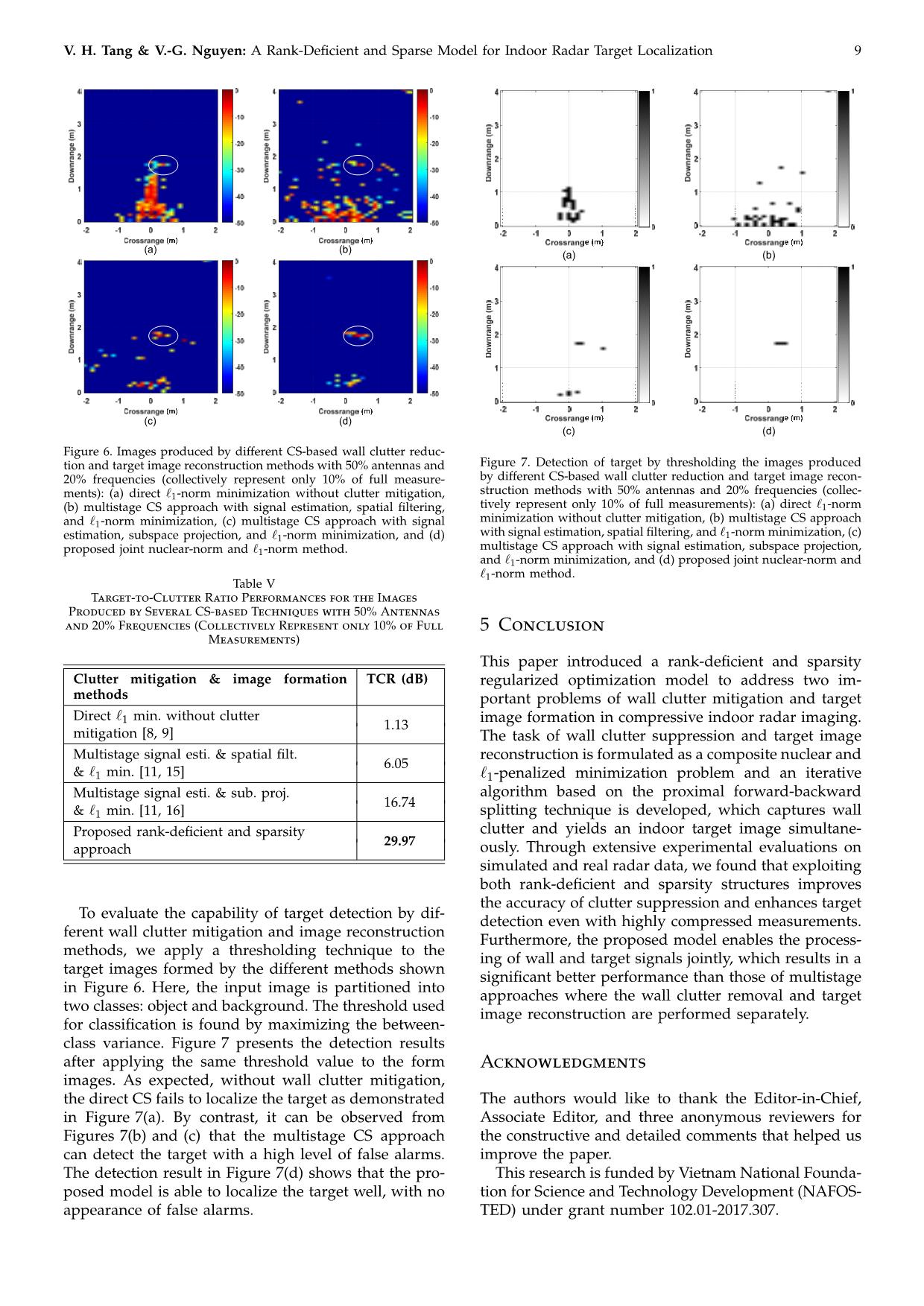
h Real Data computed and listed in Table II. As we expect from the 4.2.1 Experimental setup: Real radar datasets were visual interpretation, the proposed joint nuclear-norm collected from a scene, shown in Figure 5, that consists and `1-norm approach significantly enhances the image of one dihedral target placed behind a wooden wall. quality in terms of TCR; it yields the target image with This behind-wall scene is sensed by a 81-element linear 8 REV Journal on Electronics and Communications, Vol. 10, No. 1–2, January–June, 2020 Table III Computational Results of the Proposed Low-rank and Sparse Regularized Model for Different Noise Levels using 50% of the Total Measurements w w f (Z , st+1) f (Z , st) SNR (dB) Rank(Zw) | t+1 − t | Iterations TCR (dB) f (Zw, s ) | t t | 15 1 9.63 10 7 155 19.45 − × − 10 1 9.31 10 7 143 30.96 − × − 5 1 8.86 10 7 135 40.60 − × − 0 1 8.54 10 7 134 43.49 × − 5 1 8.34 10 7 134 43.58 × − 10 1 8.56 10 7 132 44.75 × − 15 1 8.31 10 7 130 45.86 × − Table IV Computational Results of the Low-rank and Sparse Model for Different Reduced Datasets w w f (Z , st+1) f (Z , st) Dataset Rank(Zw) | t+1 − t | Iterations TCR (dB) f (Zw, s ) | t t | 20% 1 6.90 10 7 567 25.07 × − 25% 1 7.97 10 7 368 32.26 × − 30% 1 7.59 10 7 253 34.07 × − 35% 1 8.01 10 7 203 37.64 × − 40% 1 7.71 10 7 168 38.87 × − 45% 1 8.05 10 7 144 42.59 × − 50% 1 7.84 10 7 134 44.79 × − full data volume, by randomly selecting only half of the available antennas (41 out of 81). Each selected antenna uses only 20% (160 out of 801) frequencies, which are !"#$%&' randomly sampled. Thus, the used dataset constitutes only 10% of the full data volume. For comparison, we also implement the existing direct CS and multistage CS-based approaches for wall clutter mitigation and *), + target image reconstruction using the same reduced dataset. Figure 6 depicts the target images reconstructed ()*- + using the different imaging methods. The direct CS method yields a degraded image shown in Figure 6(a) *)( + due to the presence of strong wall interferences, hin- ()(* + dering target identification. The multistage CS-based methods with the spatial filtering and subspace projec- Figure 5. Layout of the imaged scene containing a wooden wall tion produce the target images in Figures 6(b) and (c), and one dihedral used as target for through-the-wall radar data respectively. In these formed target images, strong acquisition. wall clutter is suppressed, which enables the target localization. The proposed joint low-rank and sparse model gives the image shown in Figure 6(d), where the antenna array synthesized by a monostatic radar system target pixels are highlighted and background clutter are with the inter-element spacing of 0.01 m. The radar substantially reduced. system transceives a 801-step frequency signal covering Table V presents the performance measure of TCRs the bandwidth of [1–3 GHz]. This stepped-frequency by the different CS-based techniques. It can be observed SAR system was positioned in front of the 0.16 m-thick from the table that the proposed joint nuclear-norm and wooden wall, at a standoff distance of 1.0 m. `1-norm approach outperforms the exisiting CS-based 4.2.2 Clutter mitigation & image reconstruction: This imaging techniques in terms of TCR; it has the highest experiment evaluates the proposed rank-deficient and TCR value of 29.97 dB, followed by the multistage sparse approach under generic CS operations where CS with subspace projection of 16.74 dB, multistage both antennas and frequencies are highly compressed. CS with spatial filtering of 6.05 dB, and direct CS of CS radar imaging acquires a reduced dataset, instead of 1.13 dB. V. H. Tang & V.-G. Nguyen: A Rank-Deficient and Sparse Model for Indoor Radar Target Localization 9 !" #" !" #" $" %" $" %" Figure 6. Images produced by different CS-based wall clutter reduc- tion and target image reconstruction methods with 50% antennas and Figure 7. Detection of target by thresholding the images produced 20% frequencies (collectively represent only 10% of full measure- by different CS-based wall clutter reduction and target image recon- ments): (a) direct `1-norm minimization without clutter mitigation, struction methods with 50% antennas and 20% frequencies (collec- (b) multistage CS approach with signal estimation, spatial filtering, tively represent only 10% of full measurements): (a) direct `1-norm and `1-norm minimization, (c) multistage CS approach with signal minimization without clutter mitigation, (b) multistage CS approach ` estimation, subspace projection, and `1-norm minimization, and (d) with signal estimation, spatial filtering, and 1-norm minimization, (c) proposed joint nuclear-norm and `1-norm method. multistage CS approach with signal estimation, subspace projection, and `1-norm minimization, and (d) proposed joint nuclear-norm and `1-norm method. Table V Target-to-Clutter Ratio Performances for the Images Produced by Several CS-based Techniques with 50% Antennas and 20% Frequencies (Collectively Represent only 10% of Full 5 Conclusion Measurements) This paper introduced a rank-deficient and sparsity Clutter mitigation & image formation TCR (dB) regularized optimization model to address two im- methods portant problems of wall clutter mitigation and target Direct ` min. without clutter 1 1.13 image formation in compressive indoor radar imaging. mitigation [8, 9] The task of wall clutter suppression and target image Multistage signal esti. & spatial filt. reconstruction is formulated as a composite nuclear and 6.05 & `1 min. [11, 15] `1-penalized minimization problem and an iterative Multistage signal esti. & sub. proj. algorithm based on the proximal forward-backward 16.74 & `1 min. [11, 16] splitting technique is developed, which captures wall Proposed rank-deficient and sparsity clutter and yields an indoor target image simultane- 29.97 approach ously. Through extensive experimental evaluations on simulated and real radar data, we found that exploiting both rank-deficient and sparsity structures improves the accuracy of clutter suppression and enhances target To evaluate the capability of target detection by dif- detection even with highly compressed measurements. ferent wall clutter mitigation and image reconstruction Furthermore, the proposed model enables the process- methods, we apply a thresholding technique to the ing of wall and target signals jointly, which results in a target images formed by the different methods shown significant better performance than those of multistage in Figure 6. Here, the input image is partitioned into approaches where the wall clutter removal and target two classes: object and background. The threshold used image reconstruction are performed separately. for classification is found by maximizing the between- class variance. Figure 7 presents the detection results after applying the same threshold value to the form Acknowledgments images. As expected, without wall clutter mitigation, the direct CS fails to localize the target as demonstrated The authors would like to thank the Editor-in-Chief, in Figure 7(a). By contrast, it can be observed from Associate Editor, and three anonymous reviewers for Figures 7(b) and (c) that the multistage CS approach the constructive and detailed comments that helped us can detect the target with a high level of false alarms. improve the paper. The detection result in Figure 7(d) shows that the pro- This research is funded by Vietnam National Founda- posed model is able to localize the target well, with no tion for Science and Technology Development (NAFOS- appearance of false alarms. TED) under grant number 102.01-2017.307. 10 REV Journal on Electronics and Communications, Vol. 10, No. 1–2, January–June, 2020 References tional Conference on Recent Advances in Signal Processing, Telecommunications & Computing (SigTelCom). IEEE, 2019, [1] M. G. Amin, Ed., Through-the-Wall Radar Imaging. CRC pp. 48–52. press, 2010. [18] P. L. Combettes and V. R. Wajs, “Signal recovery by [2] F. Ahmad, M. G. Amin, and S. A. Kassam, “Synthetic proximal forward-backward splitting,” SIAM J. Multi- aperture beamformer for imaging through a dielectric scale Multiscale Modeling & Simulation, vol. 4, no. 4, pp. wall,” IEEE Transactions on Aerospace and Electronic Sys- 1168–1200, 2005. tems, vol. 41, no. 1, pp. 271–283, 2005. [19] P. L. Combettes and J.-C. Pesquet, “Proximal splitting [3] V. H. Tang, S. L. Phung, F. H. C. Tivive, and methods in signal processing,” in Fixed-point algorithms A. Bouzerdoum, “A sparse Bayesian learning approach for inverse problems in science and engineering. Springer, for through-wall radar imaging of stationary targets,” 2011, pp. 185–212. IEEE Transactions on Aerospace and Electronic Systems, [20] N. Parikh and S. Boyd, “Proximal algorithms,” Founda- vol. 53, no. 5, pp. 2485–2501, 2017. tions and Trends® in Optimization, vol. 1, no. 3, pp. 123– [4] M. G. Amin and F. Ahmad, “Wideband synthetic aper- 231, 2013. ture beamforming for through-the-wall imaging,” IEEE [21] V. H. Tang, A. Bouzerdoum, S. L. Phung, and F. H. C. Signal Processing Magazine, vol. 25, no. 4, pp. 110–113, Tivive, “Enhanced through-the-wall radar imaging using 2008. Bayesian compressive sensing,” in Proceedings of the SPIE [5] D. L. Donoho, “Compressed sensing,” IEEE Transactions Compressive Sensing II, vol. 8717. International Society on Information Theory, vol. 52, no. 4, pp. 1289–1306, 2006. for Optics and Photonics, 2013, pp. 87 170I.1–87 170I.12. [6] E. J. Candes, J. K. Romberg, and T. Tao, “Stable signal re- [22] V. H. Tang, A. Bouzerdoum, and S. L. Phung, “Multi- covery from incomplete and inaccurate measurements,” polarization through-wall radar imaging using low-rank Communications on Pure and Applied Mathematics: A Jour- and jointly-sparse representations,” IEEE Transactions on nal Issued by the Courant Institute of Mathematical Sciences, Image Processing, vol. 27, no. 4, pp. 1763–1776, 2017. vol. 59, no. 8, pp. 1207–1223, 2006. [23] S. Ma, D. Goldfarb, and L. Chen, “Fixed point and Breg- [7] E. J. Candès, J. Romberg, and T. Tao, “Robust uncertainty man iterative methods for matrix rank minimization,” principles: Exact signal reconstruction from highly in- Mathematical Programming, vol. 128, no. 1-2, pp. 321–353, complete frequency information,” IEEE Transactions on 2011. Information Theory, vol. 52, no. 2, pp. 489–509, 2006. [24] J.-F. Cai, E. J. Candès, and Z. Shen, “A singular value [8] Y.-S. Yoon and M. G. Amin, “Compressed sensing tech- thresholding algorithm for matrix completion,” SIAM nique for high-resolution radar imaging,” in Proceedings Journal on Optimization, vol. 20, no. 4, pp. 1956–1982, of the Signal Processing, Sensor Fusion, and Target Recog- 2010. nition XVII, vol. 6968. International Society for Optics [25] R. T. Rockafellar, Convex analysis. Princeton University and Photonics, 2008, pp. 69 681A.1–69 681A.10. Press, 1970, no. 28. [9] Q. Huang, L. Qu, B. Wu, and G. Fang, “UWB through- [26] K. Lee and Y. Bresler, “ADMiRA: Atomic decomposition wall imaging based on compressive sensing,” IEEE for minimum rank approximation,” IEEE Transactions on Transactions on Geoscience and Remote Sensing, vol. 48, Information Theory, vol. 56, no. 9, pp. 4402–4416, 2010. no. 3, pp. 1408–1415, 2009. [27] A. Beck and M. Teboulle, “A fast iterative shrinkage- [10] V. H. Tang, A. Bouzerdoum, and S. L. Phung, “Two-stage thresholding algorithm for linear inverse problems,” through-the-wall radar image formation using compres- SIAM Journal on Imaging Sciences, vol. 2, no. 1, pp. 183– sive sensing,” Journal of Electronic Imaging, vol. 22, no. 2, 202, 2009. pp. 021 006.1–021 006.10, 2013. [11] E. Lagunas, M. G. Amin, F. Ahmad, and M. Nájar, “Joint wall mitigation and compressive sensing for indoor im- age reconstruction,” IEEE Transactions on Geoscience and Van Ha Tang received the B.Eng. degree in Remote Sensing, vol. 51, no. 2, pp. 891–906, 2012. 2005 and M.Eng. degree in 2008, all in com- [12] V. H. Tang, A. Bouzerdoum, S. L. Phung, and F. H. C. puter engineering, from Le Quy Don Technical Tivive, “Enhanced wall clutter mitigation for compressed University, Hanoi, Vietnam. In 2016, he ob- through-the-wall radar imaging using joint Bayesian tained the Ph.D. degree in computer engineer- sparse signal recovery,” in Proceedings of the IEEE Interna- ing from the University of Wollongong, Aus- tional Conference on Acoustics, Speech and Signal Processing tralia. Since 2016, he has been working as a (ICASSP). IEEE, 2014, pp. 7804–7808. Postdoctoral Research Fellow in the School of [13] F. Ahmad, J. Qian, and M. G. Amin, “Wall clutter mit- Electrical Computer and Telecommunications igation using discrete prolate spheroidal sequences for Engineering, University of Wollongong. Dr. Tang is now with the Faculty of Information sparse reconstruction of indoor stationary scenes,” IEEE Technology, Le Quy Don Technical University, Hanoi, Vietnam. His Transactions on Geoscience and Remote Sensing, vol. 53, research interests include radar imaging and through-wall radar no. 3, pp. 1549–1557, 2014. signal processing, statistical and probabilistic modeling, and inverse [14] A. Bouzerdoum, F. H. C. Tivive, and V. H. Tang, “Multi- problems in image and signal processing. polarization through-the-wall radar imaging using joint Bayesian compressed sensing,” in Proceedings of the 19th International Conference on Digital Signal Processing. IEEE, 2014, pp. 783–788. [15] Y.-S. Yoon and M. G. Amin, “Spatial filtering for wall- Van-Giang Nguyen received his B.S. degree in computer science from Le Quy Don Tech- clutter mitigation in through-the-wall radar imaging,” nical University , Hanoi, Vietnam, in 2005, IEEE Transactions on Geoscience and Remote Sensing, and his M.Sc. and Ph.D. degrees in electronic vol. 47, no. 9, pp. 3192–3208, 2009. engineering from Paichai University, Daejeon, [16] F. H. C. Tivive, A. Bouzerdoum, and M. G. Amin, “A Korea, in 2009 and 2012, respectively. Since subspace projection approach for wall clutter mitigation 2013, he has been with the Department of in through-the-wall radar imaging,” IEEE Transactions on Information Systems, Le Quy Don Techni- Geoscience and Remote Sensing, vol. 53, no. 4, pp. 2108– cal University, Hanoi, Vietnam. His current 2122, 2014. research interests include image processing, [17] H. Van Tang and V.-G. Nguyen, “A rank-deficient and computer vision, machine learning and their applications to medical physics and medical imaging. sparse penalized optimization model for compressive indoor radar imaging,” in Proceedings of the 3rd Interna-
File đính kèm:
 a_rank_deficient_and_sparse_penalized_optimization_model_for.pdf
a_rank_deficient_and_sparse_penalized_optimization_model_for.pdf

