A novel quotient prediction for floating-point division
At present, floating-point operations are used as add-on functions in critical embedded systems,
such as physics, aerospace system, nuclear simulation, image and digital signal processing, automatic
control system and optimal control and financial, etc. However, floating-point division is slower than
floating-point multiplication. To solve this problem, many existing works try to reduce the required
number
of iterations, which exploit large Look Up Table (LUT) resource to achieve approximate mantissa of a
quotient. In this paper, we propose a novel prediction algorithm to achieve an optimal quotient by
predicting certain bits in a dividend and a divisor, which reduces the required LUT resource. Therefore,
the final quotient is achieved by accumulating all predicted quotients using our proposed prediction
algorithm. The experimental results show that only 3 to 5 iterations are required to obtain the final
quotient in a floating-point division computation. In addition, our proposed design takes up 0.84% to
3.28% (1732 LUTs to 6798 LUTs) and 5.04% to 10.08% (1916 (ALUT) to 3832 (ALUT)) when ported to
Xilinx Virtex-5 and Altera Stratix-III FPGAs, respectively. Furthermore, our proposed design allows
users to track remainders and to set customized thresholds of these remainders to be compatible with a
specific application.

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7
Trang 8

Trang 9
Trang 10
Tải về để xem bản đầy đủ
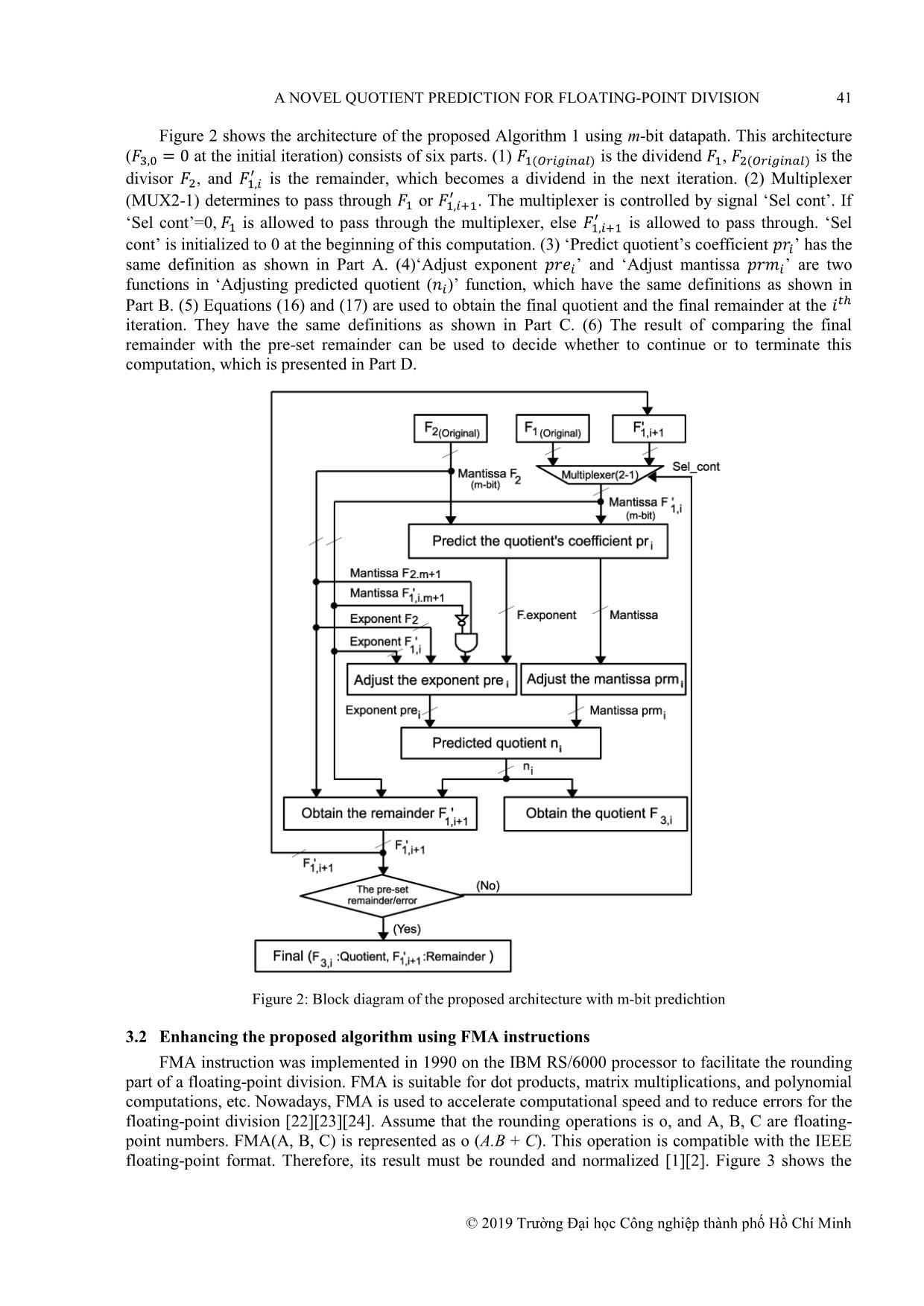
Tóm tắt nội dung tài liệu: A novel quotient prediction for floating-point division

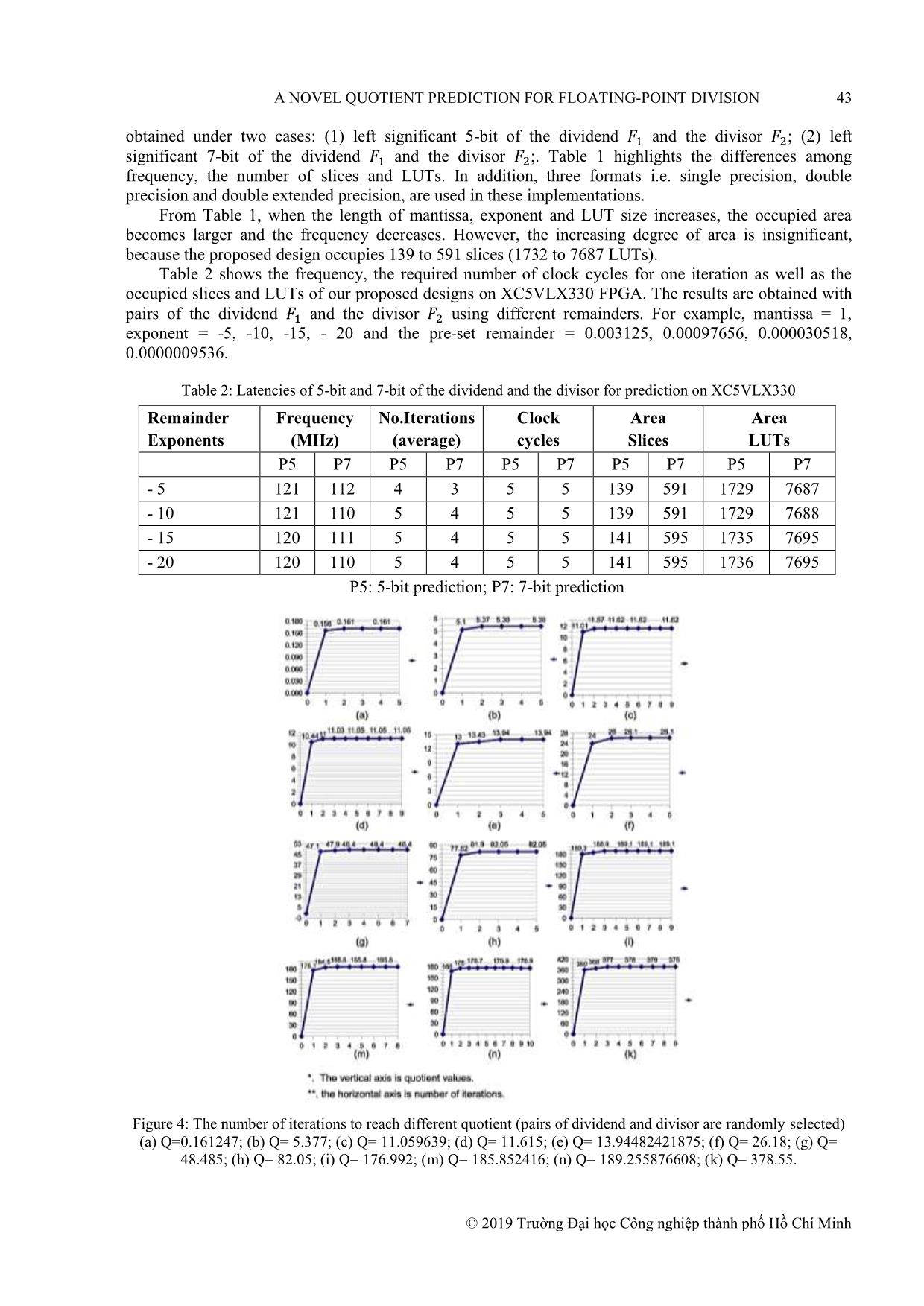
esults are © 2019 Trường Đại học Công nghiệp thành phố Hồ Chí Minh A NOVEL QUOTIENT PREDICTION FOR FLOATING-POINT DIVISION 43 obtained under two cases: (1) left significant 5-bit of the dividend and the divisor ; (2) left significant 7-bit of the dividend and the divisor ;. Table 1 highlights the differences among frequency, the number of slices and LUTs. In addition, three formats i.e. single precision, double precision and double extended precision, are used in these implementations. From Table 1, when the length of mantissa, exponent and LUT size increases, the occupied area becomes larger and the frequency decreases. However, the increasing degree of area is insignificant, because the proposed design occupies 139 to 591 slices (1732 to 7687 LUTs). Table 2 shows the frequency, the required number of clock cycles for one iteration as well as the occupied slices and LUTs of our proposed designs on XC5VLX330 FPGA. The results are obtained with pairs of the dividend and the divisor using different remainders. For example, mantissa = 1, exponent = -5, -10, -15, - 20 and the pre-set remainder = 0.003125, 0.00097656, 0.000030518, 0.0000009536. Table 2: Latencies of 5-bit and 7-bit of the dividend and the divisor for prediction on XC5VLX330 Remainder Frequency No.Iterations Clock Area Area Exponents (MHz) (average) cycles Slices LUTs P5 P7 P5 P7 P5 P7 P5 P7 P5 P7 - 5 121 112 4 3 5 5 139 591 1729 7687 - 10 121 110 5 4 5 5 139 591 1729 7688 - 15 120 111 5 4 5 5 141 595 1735 7695 - 20 120 110 5 4 5 5 141 595 1736 7695 P5: 5-bit prediction; P7: 7-bit prediction Figure 4: The number of iterations to reach different quotient (pairs of dividend and divisor are randomly selected) (a) Q=0.161247; (b) Q= 5.377; (c) Q= 11.059639; (d) Q= 11.615; (e) Q= 13.94482421875; (f) Q= 26.18; (g) Q= 48.485; (h) Q= 82.05; (i) Q= 176.992; (m) Q= 185.852416; (n) Q= 189.255876608; (k) Q= 378.55. © 2019 Trường Đại học Công nghiệp thành phố Hồ Chí Minh 44 A NOVEL QUOTIENT PREDICTION FOR FLOATING-POINT DIVISION Figure 4 shows the relationship between the different obtained quotient values and the number of iteration. In Figure 4 from (a) to (l), we randomly choose the pairs of the dividend and the divisor based on test vector sets as shown in Table 2. It is obvious that the computed quotient value is close to the required quotient value in the first iteration. It could reach the optimal condition after the second iteration and remains stable for the rest iterations. From Figure 4 and Table 2, we can draw a conclusion that approximately 3 to 5 iterations on the average are needed to obtain the final quotient. A significant speedup of convergence is achieved in the first two iterations of the computation. The speed of this convergent slows down or remains stable from the third iteration or the fourth iteration onwards. For example, the results of 10 divided by 3 can be 3.3333, 3.333333, or 3.3333333, which depends on the required precision. If the dividend is larger than the divisor, the speed of convergence to obtain the final quotient is faster. In the case that the pre-set reminder is small, the number of iterations to reach the stable state is large, which results in the longer computational time. Table 3 shows the implementation results of our proposed algorithms on XC5VLX330 and EP3SE50F484C2 FPGAs, respectively. In this particular test, the dividend is 0.100001111.27, the divisor is 0.10010001.25, the required remainder mantissa is 1, and the required remainder‟s exponent is -5. The results show that the proposed design takes up 0.84% to 3.28% (1732 LUTs to 6798 LUTs) and 5.04% to 10.08% (1916 (ALUT) to 3832 (ALUT)) on XC5VLX330 and EP3SE50F484C2 FPGAs, respectively. Table 3: The implementation results of the floating-point division on XC5VLX330 and EP3SE50F484C2 Single precision Double precision Double extended Platforms Virtex-5 Stratix III Virtex-5 Stratix III Virtex-5 Stratix III Frequency (MHz) 193 179 162 160 162 158 Number of Slices 139 1916 301 2805 548 3832 (ALUT) (ALUT) (ALUT) (0.07%) (5.04%) (0.15%) (7.38%) (0.26%) (10.8%) Number of LUTs 1732 1916 3728 2805 6798 3832 (ALUT) (ALUT) (ALUT) (0.84%) (5.04%) (1.80%) (7.38%) (3.28%) (10.08%) i (iterations) 5 5 5 5 5 5 Total time (ns) 155 196 182 230 217 263 Table 4 shows a comparison between our proposed algorithm and existing floating-point divisions for double precision. It is quite hard to make a fair comparison due to different algorithms and different platforms used in the existing works. Therefore, we focus on the comparison of number of iterations. The maximum numbers of iterations in [5] and [25] with the non-restoring algorithm and digit-current algorithm are 29 and 55. Compared to them, 13.8% and 54% reduction on maximum number of iterations has been achieved by our algorithm. The maximum number of iterations used in [7] in with Newton Raphson method is 31. Compare with this, our proposed algorithm reduces 19.4% number of iterations. The maximum number of iterations in [8] with SRT method is 40. Our proposed algorithm only requires 25 iterations. In the worst case, the maximum number of iterations of our proposed algorithm is 20% larger than the one in [17] and the same in [6]. This also proves that our proposed algorithm is able to overcome shortcomings of the SRT method, which can efficiently reduce the number of iterations and computational latency. The proposed design takes up 139 to 548 slices on Xilinx Virtex-5 FPGA, which is only 50% to 74% of the designs in [5] and [25] and reduces number of iterations with [26] using CR algorithm. © 2019 Trường Đại học Công nghiệp thành phố Hồ Chí Minh A NOVEL QUOTIENT PREDICTION FOR FLOATING-POINT DIVISION 45 Table 4: Latency comparisons between this work and previous works Works Algorith- Platform Area Total Cycle Latency ms of Time (ns) (ns) Iteratio -nns P.Echeverri‟a NRA Virtex-4 742 (Slices)** 24 ~ 29 3.6 ~ 2.9 85.7 ~ [5] 114.4 M. Schulte [6] GA K7 (FPU) - 14 ~ 26 - - GA GS1 (FPU) - 11 ~ 25 - - P. Soderquist [7] SRT-8/16 - - 8 ~ 15 7.14 57 ~ 107 NRM PA7200(FP - 14 ~ 19 7.14 107 U) NRM PA8000(FP - 31 5 155 U) S. Oberman [8] SRT – 1 SPECfp92 - > 40 - - SRT- SPECfp92 - 4 ~ 40 - - 2/4/8 T. Lang [17] SRT - 10 CMOS std - 20 1 20 (90-nm) M. Baesler [25] DRA Virtex-5 55 ~ 261 1 ~ 55 153.7 ~ 6.8 153.7 ~ 374 (Slices)* Björn Liebig CR XC5VFX20 - 10 ~ 57 5 - [26] 0T-1 This work PQC Virtex-5 139 (Slices)* 5 ~ 25 6.2 ~ 5.2 155 ~ 217 548 (Slices)** Stratix III 1916 (ALUTs)* 5 ~ 25 7.8 ~ 6.2 196 ~ 263 3832 (ALUTs)** -: not supported; *: Single precision; **: Double extended NRA: Non-restoring Algorithm; GA: Goldschmidt Algorithm SRT: The high-radix Sweeney, Robertson and Tocher Algorithm NRM: Newton-Raphson Method; DRA: Digit-Recurrent Algorithm PQC: Predicting the quotient‟s coefficient by LUT 5.2 CONCLUSIONS The floating-point division is the most complicated computations among four floating-point operations, such as addition, subtraction, multiplication and division. In order to reduce the required number of iterations, we focus on the acceleration to obtain the final quotient using the prediction of the quotient at each iteration. In our proposed algorithm, only 3 to 5 iterations are needed in order to reach final quotient in the floating-point division computation. The major advantage of our algorithm is that it is independent on different formats of floating-point number. Moreover, our proposed design utilizes FMA function, which has the advantages of obtaining the remainder easily, avoiding ”Normalize” step, and reducing effort in coding. The experimental results show that the proposed design only occupies 0.07% to 0.26% (139 slices to 548 slices) and 5.04% to 10.08% (1916 (ALUT) to 3832 (ALUT)) on Virtex-5 and Stratix-III, respectively. Furthermore, our proposed design reduces the maximum number of iterations to obtain the final quotient, with 26% to 50% reduction of the occupied area compared to the state-of-the-art works. © 2019 Trường Đại học Công nghiệp thành phố Hồ Chí Minh 46 A NOVEL QUOTIENT PREDICTION FOR FLOATING-POINT DIVISION REFERENCES [1] I. Koren, Computer Arithmetic Algorithms, AK Peters Ltd, 2002. [2] J.-M. Muller, N. Brisebarre, F.-D. Dinechin, C.-P. Jeannerod, V. Lefevre, G. Melquiond, N. Revol, D. Stehle, and S. Torres, Handbook of FloatingPoint Arithmetic, Boston-Basel-Berlin, United States, 2009. [3] T. Lang and M. D.Ercegovac, Digital Arithmetic, Morgan Kaufmann Publishers, 2004. [4] 2013. [5] P. Echeverr´ia and M. L´ opez-Vallejo, Customizing floating-point units for fpgas: Area-performance-standard trade-offs, Microprocessors and Microsystems, Available: www.elsevier.com/locate/micpro, vol. 35, pp. 535–546, 2011. [6] M. Schulte, D. Tan, and C. Lemonds, Floating-point division algorithms for an x86 microprocessor with a rectangular multiplier, in Computer Design, 2007. ICCD 2007. 25th International Conference on, October 2007, pp.304–310 [7] P. Soderquist and M. Leeser, Division and square root: choosing the right implementation, IEEE Micro, vol. 17, no. 4, pp. 56 –66, July/August 1997. [8] S. Oberman and M. Flynn, Design issues in division and other floating-point operations, IEEE Transactions on Computers, vol. 46, no. 2, pp. 154 –161, February 1997. [9] S. Obermann and M. Flynn, Division algorithms and implementations, IEEE Transactions on Computers, vol. 46, no. 8, pp. 833 –854, August 1997. [10] J.-A. Pineiro and J. Bruguera, High-speed double-precision computation of reciprocal, division, square root, and inverse square root, IEEE Transactions on Computers, vol. 51, no. 12, pp. 1377 – 1388, December 2002. [11] D. Wong and M. Flynn, Fast division using accurate quotient approximations to reduce the number of iterations, IEEE Transactions on Computers, vol. 36, pp. 850–863, 1992. [12] A. Amin and W. Shinwari, High-radix multiplier-dividers: Theory, design, and hardware, IEEE Transactions on Computers, vol. 59, no. 8, pp. 1009–1022, August 2010. [13] T.-J. Kwon and J. Draper, Floating-point division and square root using a taylor-series expansion algorithm, Microelectronics Journal, Available: www.elsevier.com/locate/mejo, vol. 40, pp. 1601–1605, 2009. [14] N. Brisebarre, J.-M. Muller, and S. K. Raina, Accelerating correctly rounded floating-point division when the divisor is known in advance, IEEE Transactions on Computers, vol. 53, no. 8, pp. 1069 – 1072, August 2004. [15] X. Wang and B. Nelson, Tradeoffs of designing floating-point division and square root on virtex fpgas, in Field-Programmable Custom Computing Machines, 2003. FCCM 2003. 11th Annual IEEE Symposium on, 2003, pp. 195–203. [16] B. P. H. Nikmehr and C. Limb, A novel implementation of radix-4 foating-point division/square-root using comparison multiples, Computers and Electrical Engineering, Available: www.elsevier.com/locate/compeleceng, vol. 36, pp. 850–863, 2010. [17] T. Lang and A. Nannarelli, A radix-10 digit-recurrence division unit: Algorithm and architecture, IEEE Transactions on Computers, vol. 56, no. 6, pp.727 –739, June 2007. [18] W. Liu and A. Nannarelli, Power efficient division and square root unit, IEEE Transactions on Computers, vol. 61, no. 8, pp. 1059 –1070, August 2012. © 2019 Trường Đại học Công nghiệp thành phố Hồ Chí Minh A NOVEL QUOTIENT PREDICTION FOR FLOATING-POINT DIVISION 47 [19] K. Quinn., The newton raphson algorithm for function optimization. Department of Political Science and The Center for Statistics and the Social Sciences, pp. 364–384, October 2001. [20] A. Y. S. Lam and V. O. K. Li, Chemical Reaction Optimization: a tutorial, 2012. [21] T. Pham, Y. Wang, and R. Li, A variable-latency floating-point division in association with predicted quotient and fixed remainder, in Circuits and Systems (MWSCAS), 2013 IEEE 56th International Midwest Symposium on, 2013, pp. 1240–1245. [22] A. Amaricai, M. Vladutiu, and O. Boncalo, Design issues and implementations for floating-point divide - add fused, Circuits and Systems II: Express Briefs, IEEE Transactions on, vol. 57, no. 4, pp. 295 –299, April 2010. [23] S. Boldo and J.-M. Muller, Exact and approximated error of the fma, IEEE Transactions on Computers, vol. 60, no. 2, pp. 157 –164, February 2011. [24] L. Huang, S. Ma, L. Shen, Z. Wang, and N. Xiao, Low-cost binary128 floating-point fma unit design with simd support, IEEE Transactions on Computers, vol. 61, no. 5, pp. 745 –751, May 2012. [25] M. Baesler, S. Voigt, and T. Teufel, Fpga implementations of radix-10 digit recurrence fixed-point and floating-point dividers, in Reconfigurable Computing and FPGAs (ReConFig), 2011 International Conference on, December 2011, pp. 13 –19. [26] Björn Liebig, Andreas Koch, Low-Latency Double-Precision Floating-PointDivision for FPGAs, 2014 International Conference on Field-Programmable Technology (FPT), pp. 25 – 32. MỘT CẢI TIẾN CHO SỰ ƯỚC LƯỢNG THƯƠNG SỐ CHO PHÉP TOÁN CHIA SỐ DẤU CHẤM ĐỘNG Tóm tắt. Ngày nay, những phép tính số dấu chấm động được sử dụng như những hàm bổ trợ trong các hệ thống nhúng tư duy ứng dụng trong các lĩnh vực như vật lý, hệ thống hàng không vũ trụ, mô phỏng hạt nhân, xử lý tín hiệu hình ảnh và kỹ thuật số, hệ thống điều khiển tự động và điều khiển tối ưu và tài chính, v.v. Tuy nhiên, phép toán chia số dấu chấm động chậm hơn so với phép toán nhân số dấu chấm động. Để giải quyết vấn đề này, đã có nhiều nghiên cứu để giảm số lượng vòng lặp cần thiết để ra thương số bằng việc dùng tài nguyên bảng tra (LUT) để đạt tới xấp sỉ gần giá trị thương số. Trong bài báo này, chúng tôi đề xuất một thuật toán ước lượng cải tiến để đạt đến một thương số tối ưu bằng sự tiên đoán những bit nhất định trong số chia và số bị chia, giảm tài nguyên LUT cần thiết. Do đó, thương số cuối cùng đạt được bằng cách tích lũy tất cả các thương số tiên đoán của giải thuật tiên đoán của chúng tôi đề xuất. Kết quả thực nghiệm cho thấy chỉ cần từ 3 đến 5 vòng lặp để có được thương số cuối cùng trong phép chia số dấu chấm động. Thêm nữa, thiết kế được đề xuất chiếm 0.84% đến 3.28% (1732 LUTs đến 6798 LUTs) và 5.04% đến 10.08% (1916 (ALUT) đến 3832 (ALUT)) khi được cài đặt trên chip Xilinx Virtex-5 và Altera Stratix-III FPGAs tương ứng. Hơn nữa, thiết kế đề xuất cho phép những người sử dụng theo dõi phần dư để đặt ngưỡng tùy chỉnh cho số dư tương thích với những ứng dụng chuyên biệt của người sử dụng. Từ khóa. Số dấu chấm động, phép toán chia số dấu chấm động, đơn vị xử lý số dấu chấm động (FPU), FPGA, bảng tra (LUT), hệ thống nhúng. Ngày nhận bài:08/08/2019 Ngày chấp nhận đăng:25/10/2019 © 2019 Trường Đại học Công nghiệp thành phố Hồ Chí Minh
File đính kèm:
 a_novel_quotient_prediction_for_floating_point_division.pdf
a_novel_quotient_prediction_for_floating_point_division.pdf

