A new method for solving the mgrlw equation using a base of quintic B-Spline

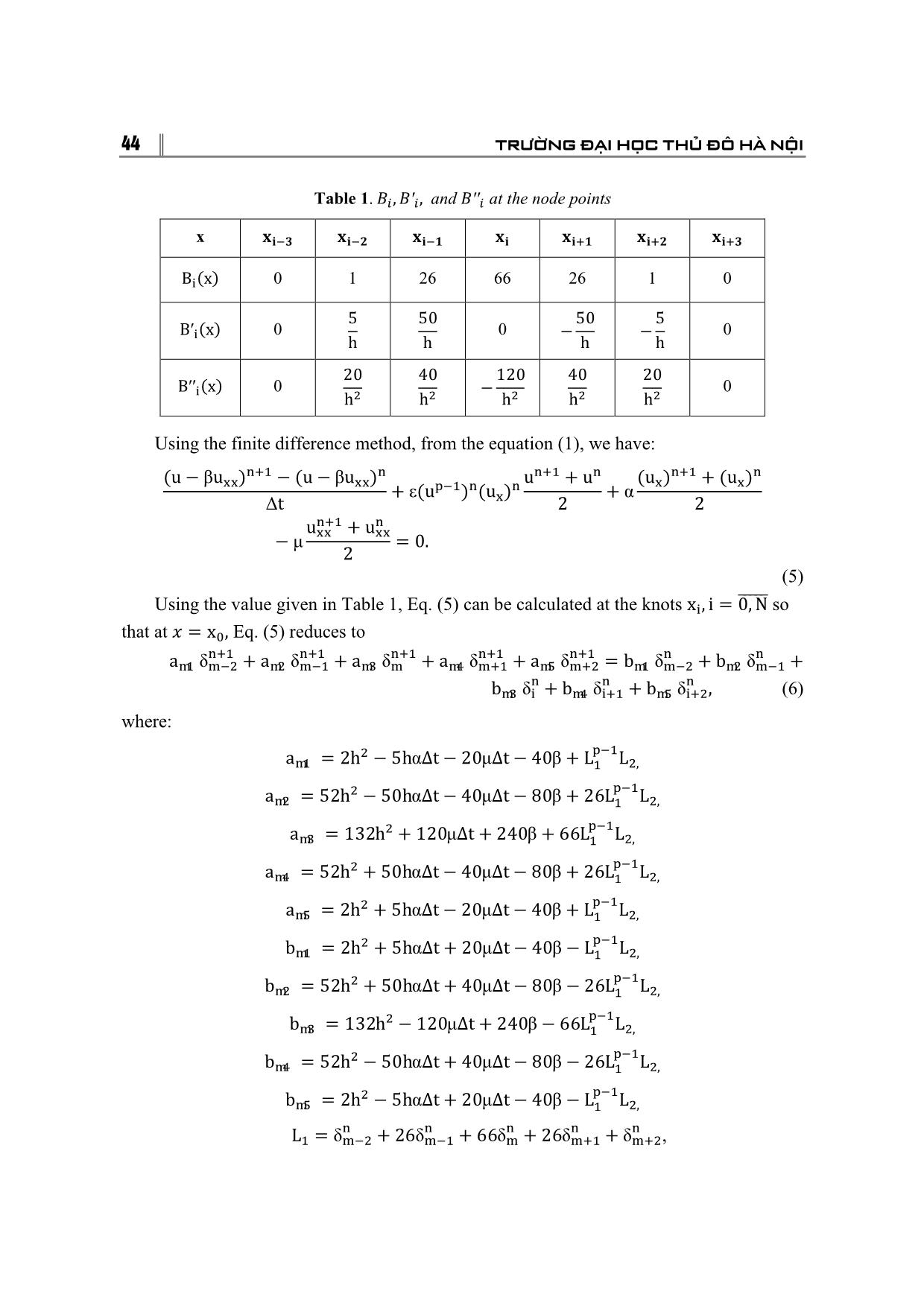
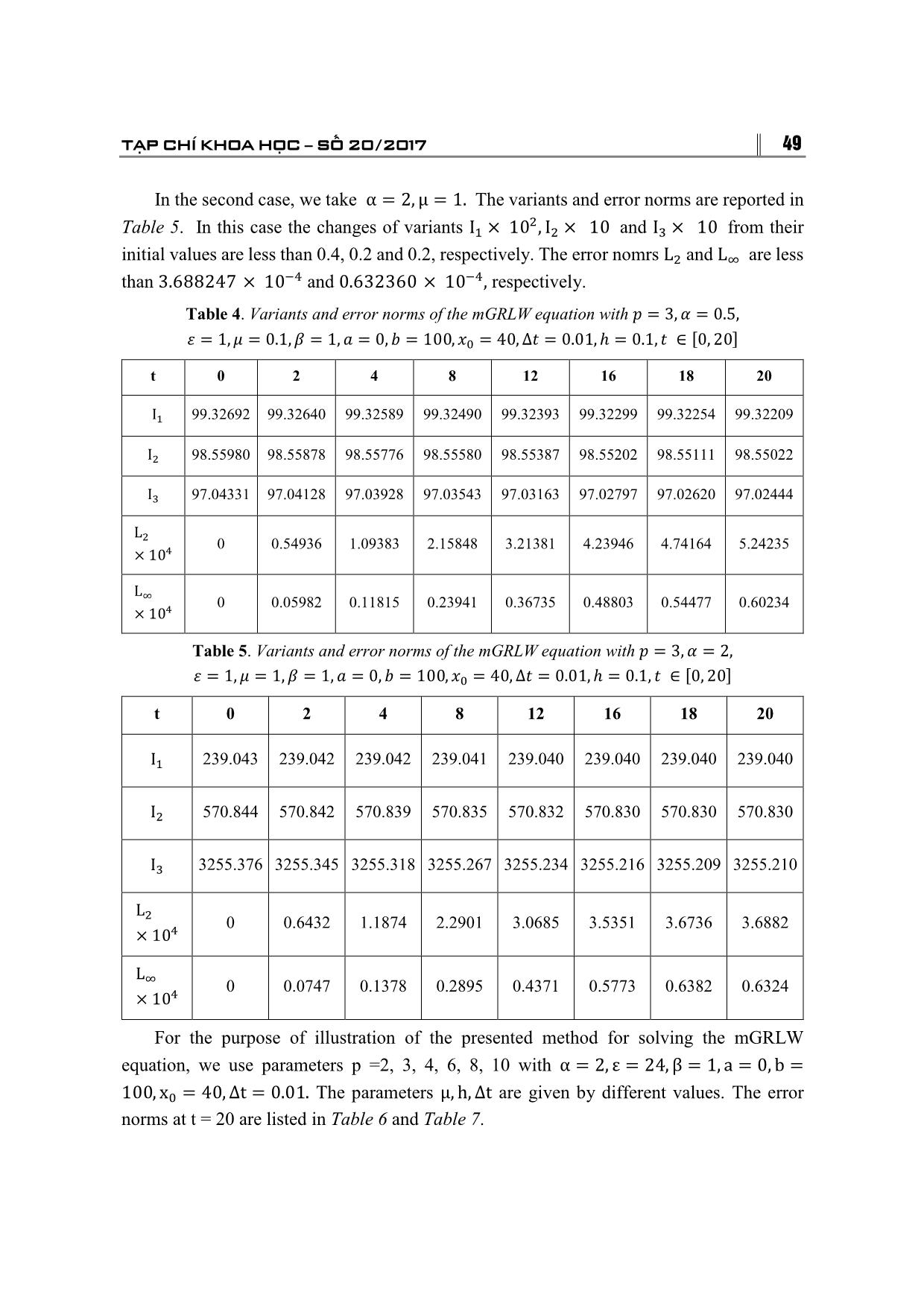
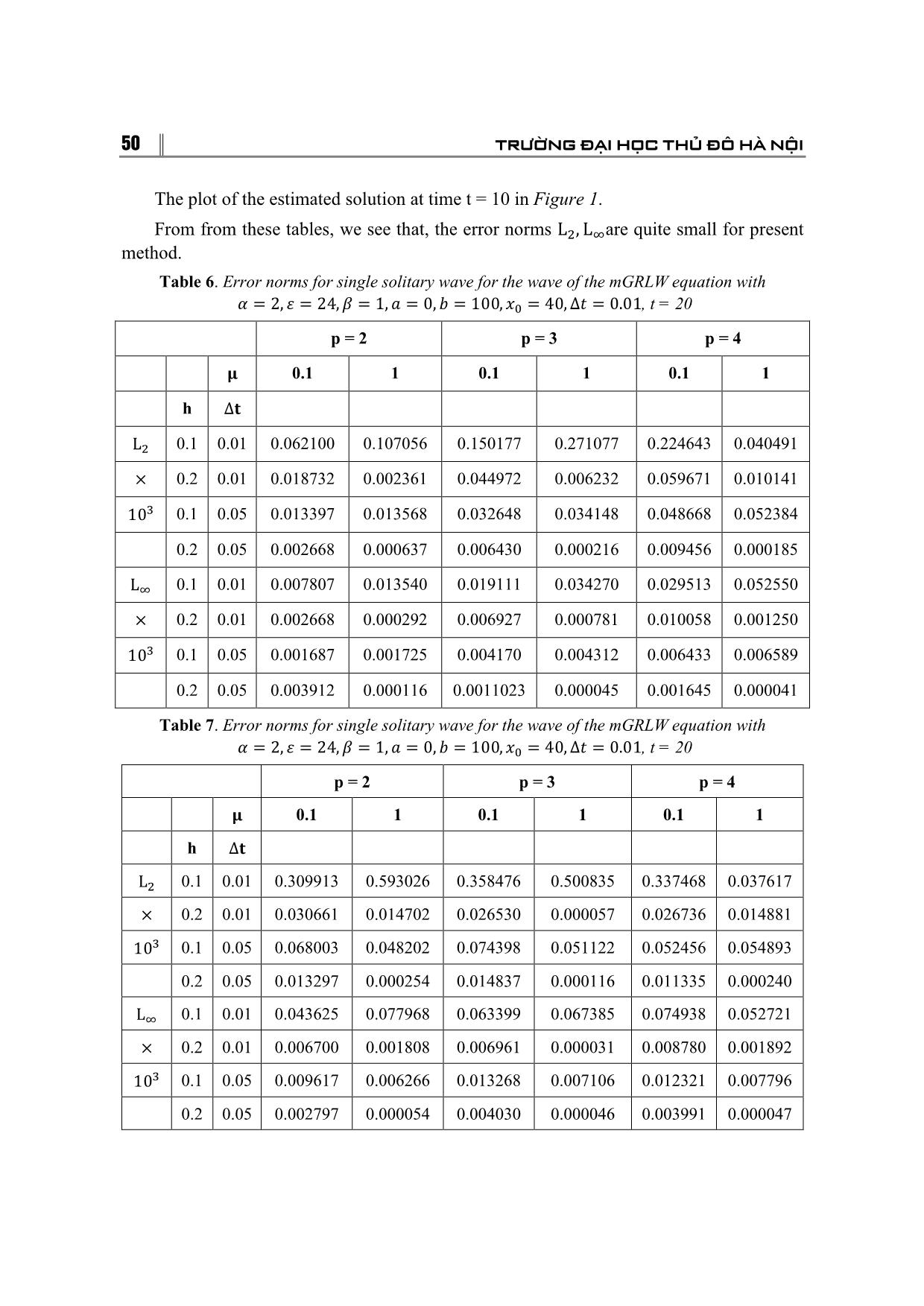
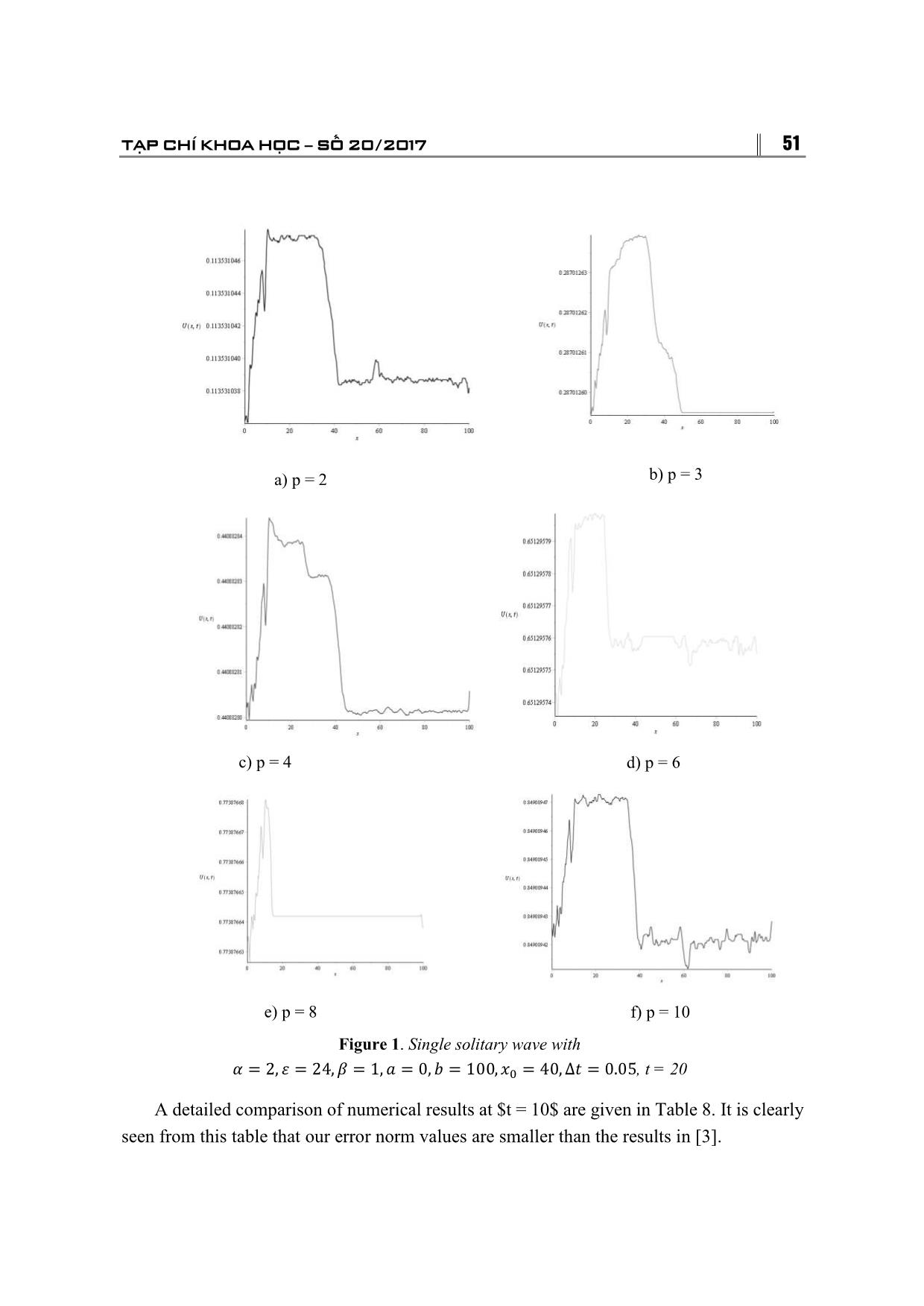
= (δ, δ,  , δ) , r = (f(x), f(x),  , f(x)) . 
46   TRƯỜNG ĐẠI HỌC THỦ ĐÔ HÀ NỘI 
3. STABILITY ANALYSIS 
 To apply the Von-Neumann stability for the system (6), we must first linearize this 
system. 
 We have: 
  
 δ = ξ exp(iγjh) , i = √−1,        (10) 
where γ is the mode number and h is the element size. 
 
 Being applicable to only linear schemes the nonlinear term U U is linearized by taking 
U as a  locally constant value c. The linearized form of proposed scheme is given as 
        
 pδ + pδ + pδ + pδ + pδ = p′δ + p′δ + p′δ +
  
 + p′δ + p′δ  (11) 
where 
 p = 1 − M − N − P, p = 26 − 10M − 2N − 2P, p = 66 + 6N + 6P, 
   p = 26 + 10M − 2N − 2P, p = 1 + M − N − P, 
 ′ ′
   p′ = 1 + M + N − P, p  = 26 + 10M + 2N − 2P, p  = 66 − 6N + 6P, 
   p′ = 26 − 10M + 2N − 2P, p′ = 1 − M + N − P, 
 5(α + εc)∆t 10μ∆t 10β
 M = , N = , P = . 
 h  h h
  
 Substitretion of δ = exp(iγjh)ξ ,into Eq. (11) leads to  
 ξ[p exp(−2ihγ) + p exp(−iγh) + p + p exp(iγh) + p exp(2iγh)] =
 p exp(−2iγh) + p exp(−iγh) + p + p exp(iγh) + p′ exp(2iγh). (12) 
 Simplifying Eq. (13), we get: 
 A − iB
  =  , 
 C + iB 
where 
 A = 2(1 + N − P) cos(2ϕ) + 4(13 + N − P)cosϕ + 66− 6N + 6P, 
 B = 2M(sin( 2ϕ) + 10), 
 C = 2(1 − N − P) cos(2ϕ) + 4(13 − N − P)cosϕ + 66 + 6N + 6P, 
 ϕ = γh. 
TẠP CHÍ KHOA HỌC SỐ 20/2017   47 
  
 It is clear that C ≥ A. So || ≤ 1. 
 Therefore, the linearized numerical scheme for the mGRLW equation is unconditionally 
stable. 
4. NUMERICAL EXAMPLE 
 We now obtain the numerical solution of the mGRLW equation for some problems. To 
show the efficiency of the present method for our problem in comparison with the exact 
solution, we report L∞ and L using formula: 
 L = max|U(x, t) − u(x, t)|, 
 
 
 
 L = h |U(x, t) − u(x, t)|  , 
 
where U is numerical solution and u denotes exact solution. 
 Three invariants of motion which correspond to the conservation of mass, momentum, 
and energy are given as: 
   
    2β(p + 1) 
 I =  udx, I =  (u + βu)dx, I =  u − u dx. 
    ε
 Using the method [8], we find the exact solution of the mGRLW is: 
 
 3 sinh(kx + ωt + x ) + 5 cosh(kx + ωt + x ) 
 u(x, t) = ρ 1 +    , 
 3 cosh(kx + ωt + x) + 5 sinh(kx + ωt + x)
  
where ρ =  αβ(p + 5p + 4 + (p + 1)A ), k = (−αβ(p + 4) + A ), 
 ()  () 
 
 ω = , A = β(p + 4)[αβ(p + 4) − 8μ]. 
 () 
 The initial condition of Equation (1) given by: 
 
 3 sinh(kx + x ) + 5 cosh(kx + x ) 
 f(x) = ρ 1 +    . 
 3 cosh(kx + x) + 5 sinh(kx + x)
 We take p = 2, α = 2, ε = 24, μ = 1, β = 1, a = 0, b = 100, x = 40, ∆t = 0.025 and 
∆t = 0.01, h = 0.1 and h = 0.2, t ∈ [0, 20]. The values of the variants and the error norms 
at several times are listed in Table 2 and Table 3. From Table 2, we see that, changes of 
   
variants I × 10 , I × 10  and I × 10 from their initial value are less than 0.2, 0.5 and 
48   TRƯỜNG ĐẠI HỌC THỦ ĐÔ HÀ NỘI 
 
0.2,  respectively.  The  error  nomrs  L, L  are  less  than  0.214669 × 10   and 
0.027200 × 10, respectively.  
   
 In Table 3, changes of variants I × 10 , I × 10  and I × 10 from their initial value 
are  less  than  0.3,  0.5  and  0.2,  respectively.  The  error  nomrs  L, L  are  less  than 
0.236126 × 10 and 0.029150 × 10, respectively.  
 Table 2. Variants and error norms of the mGRLW equation with  = 2,  = 2, 
  = 24,  = 1,  = 1,  = 0,  = 100,  = 40, ∆ = 0.025, ℎ = 0.1,  ∈ [0, 20] 
 t 0 5 10 15 20 
 I  11.364457  11.364400  11.364348  11.364304  11.364267 
 I  1.290217  1.290206  1.290104  1.290184  1.290175 
 I  0.016630  0.016630  0.016629  0.016629  0.016629 
 
 L × 10     0  0.061154  0.118178  0.169317  0.214669 
 
 L × 10     0  0.006843  0.013690  0.020430  0.027200 
 Table 3. Variants and error norms of the mGRLW equation with p = 2, α = 2, 
 ε = 24, μ = 1, β = 1, a = 0, b = 100, x = 40, ∆t = 0.01, h = 0.2, t ∈ [0, 20] 
 t 0 5 10 15 20 
 I  11.375810  11.375816  11.375821  11.375827  11.375831 
 I  1.291507  1.291509  1.291510  1.291511  1.291512 
 I  0.016647  0.016647  0.016647  0.016647  0.016647 
 
 L × 10     0  0.058625  0.121810  0.179241  0.236126 
 
 L × 10     0  0.007040  0.014610  0.021330  0.029150 
 To get more the variants and error norms, we choose two sets of parameters by taking 
different values of α, μand the same values of ε = 1, β = 1, a = 0, b = 100, x = 40, ∆t =
0.01, h = 0.1  The variants and error norms are calculated from time t = 0 to t = 20. 
 In the first case, we take α = 0.5, μ = 0.1. The variants and error norms are listed in 
 
Table 4. In this table, we get, the changes of variants I × 10 , I × 10 and I × 10 from 
their initial values are less than 0.5, 0.1 and 0.2, respectively. The error nomrs Land L are 
less than 5.242345 × 10 and0.602344 × 10, respectively.  
TẠP CHÍ KHOA HỌC SỐ 20/2017   49 
 In the second case, we take  α = 2, μ = 1.  The variants and error norms are reported in 
 
Table 5.  In this case the changes of variants I × 10 , I × 10  and I × 10  from their 
initial values are less than 0.4, 0.2 and 0.2, respectively. The error nomrs L and L  are less 
than 3.688247 × 10 and 0.632360 × 10, respectively. 
 Table 4. Variants and error norms of the mGRLW equation with  = 3,  = 0.5, 
  = 1,  = 0.1,  = 1,  = 0,  = 100,  = 40, ∆ = 0.01, ℎ = 0.1,  ∈ [0, 20] 
 t 0 2 4 8 12 16 18 20 
 I  99.32692  99.32640  99.32589  99.32490  99.32393  99.32299  99.32254  99.32209 
 I  98.55980  98.55878  98.55776  98.55580  98.55387  98.55202  98.55111  98.55022 
 I  97.04331  97.04128  97.03928  97.03543  97.03163  97.02797  97.02620  97.02444 
 L
  0  0.54936  1.09383  2.15848  3.21381  4.23946  4.74164  5.24235 
 × 10 
 L
  0  0.05982  0.11815  0.23941  0.36735  0.48803  0.54477  0.60234 
 × 10 
 Table 5. Variants and error norms of the mGRLW equation with  = 3,  = 2, 
  = 1,  = 1,  = 1,  = 0,  = 100,  = 40, ∆ = 0.01, ℎ = 0.1,  ∈ [0, 20] 
 t 0 2 4 8 12 16 18 20 
 I  239.043  239.042  239.042  239.041  239.040  239.040  239.040  239.040 
 I  570.844  570.842  570.839  570.835  570.832  570.830  570.830  570.830 
 I  3255.376  3255.345  3255.318  3255.267  3255.234  3255.216  3255.209  3255.210 
 L
  0  0.6432  1.1874  2.2901  3.0685  3.5351  3.6736  3.6882 
 × 10 
 L
  0  0.0747  0.1378  0.2895  0.4371  0.5773  0.6382  0.6324 
 × 10 
 For  the  purpose  of  illustration  of  the  presented  method  for  solving  the  mGRLW 
equation,  we  use  parameters  p  =2,  3,  4,  6,  8,  10  with  α = 2, ε = 24, β = 1, a = 0, b =
100, x = 40, ∆t = 0.01. The parameters μ, h, ∆t are given by different values. The error 
norms at t = 20 are listed in Table 6 and Table 7.  
50   TRƯỜNG ĐẠI HỌC THỦ ĐÔ HÀ NỘI 
 The plot of the estimated solution at time t = 10 in Figure 1.  
 From from these tables, we see that, the error norms L, Lare quite small for present 
method. 
 Table 6. Error norms for single solitary wave for the wave of the mGRLW equation with 
  = 2,  = 24,  = 1,  = 0,  = 100,  = 40, ∆ = 0.01, t = 20 
 p = 2 p = 3 p = 4 
  0.1 1 0.1 1 0.1 1 
 h ∆ 
 L  0.1  0.01  0.062100  0.107056  0.150177  0.271077  0.224643  0.040491 
 ×  0.2  0.01  0.018732  0.002361  0.044972  0.006232  0.059671  0.010141 
10  0.1  0.05  0.013397  0.013568  0.032648  0.034148  0.048668  0.052384 
   0.2  0.05  0.002668  0.000637  0.006430  0.000216  0.009456  0.000185 
L  0.1  0.01  0.007807  0.013540  0.019111  0.034270  0.029513  0.052550 
 ×  0.2  0.01  0.002668  0.000292  0.006927  0.000781  0.010058  0.001250 
10  0.1  0.05  0.001687  0.001725  0.004170  0.004312  0.006433  0.006589 
   0.2  0.05  0.003912  0.000116  0.0011023  0.000045  0.001645  0.000041 
 Table 7. Error norms for single solitary wave for the wave of the mGRLW equation with 
  = 2,  = 24,  = 1,  = 0,  = 100,  = 40, ∆ = 0.01, t = 20 
 p = 2 p = 3 p = 4 
  0.1 1 0.1 1 0.1 1 
 h ∆ 
 L  0.1  0.01  0.309913  0.593026  0.358476  0.500835  0.337468  0.037617 
 ×  0.2  0.01  0.030661  0.014702  0.026530  0.000057  0.026736  0.014881 
 10  0.1  0.05  0.068003  0.048202  0.074398  0.051122  0.052456  0.054893 
   0.2  0.05  0.013297  0.000254  0.014837  0.000116  0.011335  0.000240 
 L  0.1  0.01  0.043625  0.077968  0.063399  0.067385  0.074938  0.052721 
 ×  0.2  0.01  0.006700  0.001808  0.006961  0.000031  0.008780  0.001892 
 10  0.1  0.05  0.009617  0.006266  0.013268  0.007106  0.012321  0.007796 
   0.2  0.05  0.002797  0.000054  0.004030  0.000046  0.003991  0.000047 
TẠP CHÍ KHOA HỌC SỐ 20/2017   51 
 a) p = 2  b) p = 3 
   c) p = 4  d) p = 6 
   e) p = 8  f) p = 10 
   Figure 1. Single solitary wave with 
  = 2,  = 24,  = 1,  = 0,  = 100,  = 40, ∆ = 0.05, t = 20 
 A detailed comparison of numerical results at $t = 10$ are given in Table 8. It is clearly  
seen from this table that our error norm values are smaller than the results in [3]. 
 52   TRƯỜNG ĐẠI HỌC THỦ ĐÔ HÀ NỘI 
 Table 8. Error norms for single solitary wave for the wave of the mGRLW equation with 
  = 1,  = 1,  = 1,  = 0.5,  = 0,  = 1,  = 30, ∆ = 0.1, t = 10 
 p = 2 p = 4 p = 8 
 Methods LIAS Our BCS LIAS Our BCS LIAS Our BCS 
 h 
 L  0.25  63.77969  0.00023  63.16492  0.000008  11.50448  0.00007 
 ×  0.125  15.82597  0.00084  15.68213  0.00008  2.98155  0.00113 
 10  0.0625  3.92074  0.00141  3.88572  0.00182  0.74262  0.00075 
   0.03125  0.95011  0.01380  94.16614  0.00140  0.18014  0.00788 
 L  0.25  93.52639  0.00042  92.62624  0.000007  18.22979  0.00010 
 ×  0.125  23.14686  0.00212  22.94480  0.00010  4.67495  0.00200 
 10  0.0625  5.89364  0.00218  5.82816  0.00290  1.16764  0.00140 
   0.03125  1.42826  0.01922  1.41245  0.00165  0.28796  0.01126 
 5. CONCLUSION 
 In this work, we have used the quintic B - spline collocation method for solution of the 
 mGRLW equation. We tasted our scheme through single solitary wave and the obtained 
 results are tabulaces. These tables show that, the changes of variants are quite small. The 
 error norms L, L for the inviscid and mGRLW equation are better than the ones in previous 
 methods. So the present method is more capable for solving these equations. 
 REFERENCES 
1. S.S.Askar  and  A.A.Karawia  (2015),  “On  solving  pentadiagonal  linear  systems  via 
 transformations”, Mathematical Problems in Engineering, Vol. 2015, pp.1-9.   
2. S.Battal Gazi Karakoça, Halil Zeybek (2016), “Solitary - wave solutions of the GRLW equation 
 using septic B - spline collocation method”, Applied Mathematics and Computation, Vol. 289, 
 pp.159-171.  
3. H.Che, X.Pan, L.Zhang and  Y.Wang (2012), “Numerical analysis of a linear - implicit average 
 scheme for generalized Benjamin - Bona - Mahony - Burgers equation”, J. Applied Mathematics, 
 Vol. 2012, pp.1-14. 
 TẠP CHÍ KHOA HỌC SỐ 20/2017   53 
4. D.J.Evans  and  K.R.Raslan  (2005),  “Solitary  waves  for  the  generalized  equal  width  (GEW) 
 equation”, International J. of Computer Mathematics, Vol. 82(4), pp.445-455. 
5. C.M.García - Lospez, J.I.Ramos (2012), “Effects of convection on a modified GRLW equation”, 
 Applied Mathematics and Computation, Vol. 219, pp.4118-4132. 
6. C.M.García  -  Lospez,  J.I.Ramos  (2015),  “Solitari  waves  generated  by  bell  -  shaped  initial 
 conditions in the invicis and viscous GRLW equations”, Applied Mathematical Modelling, Vol. 
 39 (21), pp.6645-6668. 
7. P.A.Hammad, M.S.EI – Azab (2015), “A 2N order compact finite difference method for solving 
 the  generalized  regularized  long  wave  (GRLW)  equation”,  Applied Mathematics and 
 Computation, Vol. 253, pp.248-261. 
8. B.Hong,  D.Lu  (2008),  “New  exact  solutions  for  the  generalized  BBM  and  Burgers  -  BBM 
 equations”, World Journal of Modelling and Simulation, Vol. 4(4), pp.243-249. 
9. S.Islam,  F.Haq  and  I.A.Tirmizi  (2010),  “Collocation  method  using  quartic  B-spline  for 
 numerical solution of the modified equal width wave equation”, J. Appl. Math. Inform., Vol. 
 28(3 - 4), pp.611-624.  
10. A.G.Kaplan,  Y.Dereli  (2017),  “Numerical  solutions  of  the  GEW  equation  using  MLS 
 collocation  method”,  International Journal of Modern Physics C,  Vol.  28(1),  1750011,  
 pp.1-23.  
11. M.Mohammadi, R.Mokhtari (2011), “Solving the generalized regularized long wave equation 
 on the basis of a reproducing kernel space”, J. of Computation and Applied Mathematics, Vol. 
 235, pp.4003-4014. 
12. R.Mokhtari,  M.Mohammadi  (2010),  “Numerical  solution  of  GRLW  equation  using  sinc  - 
 collocation method”, Computer Physics Communications, Vol. 181, pp.1266-1274. 
13. E.Pindza and E.Maré (2014), “Solving the generalized regularized long wave equation using a 
 distributed  approximating  functional  method”,  International Journal of Computational 
 Mathematics, Vol. 2014, pp.1-12. 
14. P.M.Prenter (1975), “Splines and Variational Methods”, Wiley, New York.  
15. T.Roshan (2011), “A Petrov – Galerkin method for solving the generalized equal width (GEW) 
 equation”, J. Comput. Appl. Math., Vol. 235, pp.1641-1652. 
16. T.Roshan (2012), “A Petrov – Galerkin method for solving the generalized regularized long 
 wave (GRLW) equation”, Computers and Mathematics with Applications, Vol. 63, pp.943-956.  
17. M.Zarebnia and R.Parvaz (2013), “Cubic B-spline collocation method for numerical solution of 
 the Benjamin - Bona - Mahony - Burgers equation”, International Journal of Mathematical, 
 Computational, Physical, Electrical and Computer Engineering, Vol. 7 (3), pp.540-543. 
18. H.Zeybek and S.Battal Gazi Karakoça (2017), “Application of the collocation method with B - 
 spline to the GEW equation”, Electronic Transactions on Numerical Analysis, Vol. 46, pp.71-88.  
19. L.Zhang (2005), “A finite difference scheme for generalized regularized long wave equation”, 
 Applied Mathematics and Computation, Vol. 168, pp.962-972. 
20. J.Wang,  F.Bai  and  Y.Cheng  (2011),  “A  meshless  method  for  the  nonlinear  generalized 
 regularized long wave equation”, Chin. Phys. B, Vol. 20(3), 030206, pp.1-8. 
54   TRƯỜNG ĐẠI HỌC THỦ ĐÔ HÀ NỘI 
 PHƯƠNG PHÁP MỚI GIẢI PHƯƠNG TRÌNH MGRLW 
 SỬ DỤNG CƠ SỞ B – SPLINE BẬC 5 
 Tóm tắt: Trong bài báo này, nghiệm số của phương trình mGRLW sẽ tìm được dựa trên cơ 
 sở phương pháp mới sử dụng cơ sở B – spline bậc 5. Sử dụng phương pháp Von – Neumann 
 hệ phương trình sai phân ổn định vô điều kiện. Thuật toán được với sóng đơn được áp dụng 
 giải một số ví dụ. Kết quả số chứng tỏ phương pháp đưa ra hữu hiệu để giải phương 
 trình trên. 
 Từ khóa: Phương trình mGRLW, spline bậc 5, phương pháp collocation, phương pháp sai 
 phân hữu hạn.