A new method against attacks on networked industrial control systems

roblems. In this paper, we use the CUSUM statistic because it is very similar to the SPRT. 
Given a fixed false alarm rate, the CUSUM algorithm attempts to minimize the time N (where N > ks) for which the 
test stops and decides that a change has occurred. Let S(0) = 0. The CUSUM statistic is updated according to 
 1
0
( ( ))
( 1) log ( )
( ( ))
p z k
S k S k
p z k
 (16) 
where (a)
+
 = a if a ≥ 0 and zero otherwise. The stopping time is: inf { : ( ) }
n
N n S n  (17) 
for a given threshold τ selected based on the false alarm constraint. 
We can see that the CUSUM algorithm is an SPRT test with L = 0, U = τ , and whenever the statistic reaches the 
lower threshold L, it restarts. We now describe how to adapt the results of change detection theory to the particular 
problem of detecting compromised sensors. In the following, we use the subscript i to denote the sequence 
corresponding to sensor i. 
One problem that we have in our case is that we do not know the probability distribution for an attack p1. In 
general, an adaptive adversary can select any arbitrary (and possibly) non-stationary sequence zi(k). Assuming a fixed 
p1 will thus limit our ability to detect a wide range of attacks. 
To avoid making assumptions about the probability distribution of an attacker, we use ideas from nonparametric 
statistics. We do not assume a parametric distribution for p1 and p0; instead, only place mild constraints on the 
observation sequence. One of the simplest constraints is to assume the expected value of the random process Zi(k) that 
generates the sequence zi(k) under H0 is less than zero (  0 0iZ ) and the expected value of Zi(k) under H1 is greater 
than zero (  1 0iZ ). 
To achieve these conditions let us define ˆ( ) ( ) ( )i i i iz k y k y k b (18) 
where bi is a small positive constant chosen such that 0 ˆ( ) ( ) 0i i iy k y k b (19) 
The nonparametric CUSUM statistic for sensor i is then: ( ) ( ( 1) ( )) , (0) 0i i i iS k S k z k S
 (20) 
and the corresponding decision rule is 1
,
0
 if ( )
( ( ))
i i
N i i
H S k
d d S k
H otherwise

 
 (21) 
where τi is the threshold selected based on the false alarm rate for sensor i. 
Following [1], we state the following two important results for Equation (20)-(21): 
 The probability of false alarm decreases exponentially as the threshold τi increases, 
 The time to detect an attack, (Ni − ks,i)
+
, is inversely proportional to bi. 
D. Stealthy Attacks 
A fundamental problem in intrusion detection is the existence of adaptive adversaries that will attempt to evade the 
detection scheme; therefore, we now consider an adversary that knows about our anomaly detection scheme. We take a 
conservative approach in our models by assuming a very powerful attacker with knowledge of: (1) the exact linear 
model that we use (i.e., matrices A, B, and C), the parameters (τi and bi), and (3) the control command signals. Such a 
powerful attacker may be unrealistic in some scenarios, but we want to test the resiliency of our system to such an 
attacker to guarantee safety for a wide range of attack scenarios. 
The goal of the attacker is to raise the pressure in the tank without being detected (i.e., raise the pressure while 
keeping the statistic he controls below the corresponding threshold τi). We model three types of attacks: surge attacks, 
bias attacks and geometric attacks. Surge attacks model attackers that want to achieve maximum damage as soon as 
they get access to the system. A bias attack models attackers that try to modify the system discretely by adding small 
perturbations over a large period of time. Finally, geometric attacks model attackers that try to shift the behavior of the 
14 A NEW METHOD AGAINST ATTACKS ON NETWORKED INDUSTRIAL CONTROL SYSTEMS 
system very discretely at the beginning of the attack and then maximize the damage after the system has been moved to 
a more vulnerable state. 
E. Surge Attacks 
In a surge attack the adversary tries to maximize the damage as soon as possible, but when the statistic reaches the 
threshold, it then stays at the threshold level: Si(k) = τ for the remaining time of the attack. To stay at the threshold, the 
attacker needs to solve the following quadratic equation: 
2
ˆ( ) ( ) ( )i i i i iS k y k y k b  (22) 
The resulting attack (for y2 and y1) is: 
min if S ( 1)
( )
ˆ ( ) ( ) if ( 1)
i i i
i
i i i i i i
y k
y k
y k b S k S k

 
 (23) 
For y3 we use 
3
3 3
min
3 3
3
3 3 3 3
 if S ( )
( )
ˆ ( ) ( ) if ( )
y
y y
y k
y k
y k b S k S k

 
 (24) 
F. Bias Attacks 
In a bias attack the attacker adds a small constant ci at each time step. 
 , ,ˆi k i k i iy y c Y (25) 
In this case, the nonparametric CUSUM statistic can be written as 
1
0
ˆ( ) ( ) ( )
n
i i i i
k
S n y k y k nb
  (26) 
Assuming the attack starts at time k = 0 and assuming the attacker wants to be undetected for n time steps the 
attacker needs to solve the following equation 
1
0
n
i i i
k
c nb
  (27) 
Therefore ci = τi/n + b. This attack creates a bias of τi/n + bi for each attacked signal. 
This equation shows the limitations of the attacker. If an attacker wants to maximize the damage (maximize the bias 
of a signal), the attacker needs to select the smallest n it can find. Because i iy Y this attack reduces to an impulse 
attack. 
If an attacker wants to attack for a long time, then n will be very large. If n is very large then the bias will be 
smaller. 
G. Geometric Attacks 
In a geometric attack, the attacker wants to drift the value very slowly at the beginning and maximize the damage at 
the end. This attack combines the slow initial drift of the bias attack with a surge attack at the end to cause maximum 
damage. 
Let α ∈ (0, 1). The attack is ˆ( ) ( ) n ki i i iy k y k  
 (28) 
Now we need to find α and β such that Si(n) = τi. 
Assume the attack starts at time k = 0 and the attacker wants to be undetected for n time steps. The attacker then 
needs to solve the following equation: 
1
0
n
n k
i i i i
k
nb 
  (29) 
This addition is a geometric progression 
1 1
1
1
0 0
1
( )
1
nn n
n k n k i
i i i i i i
k k i
  
  (30) 
By fixing α the attacker can select the appropriate β to satisfy the above equation. 
III. RESPONSE TO ATTACKS 
A comprehensive security posture for any system should include mechanisms for prevention, detection, and 
response to attacks. Automatic response to computer attacks is one of the fundamental problems in information 
assurance. While most of the research efforts found in the literature focus on prevention (authentication, access 
controls, cryptography etc.) or detection (intrusion detection systems), in practice there are quite a few response 
mechanisms. 
Nguyen Dao Truong, Le My Tu 15 
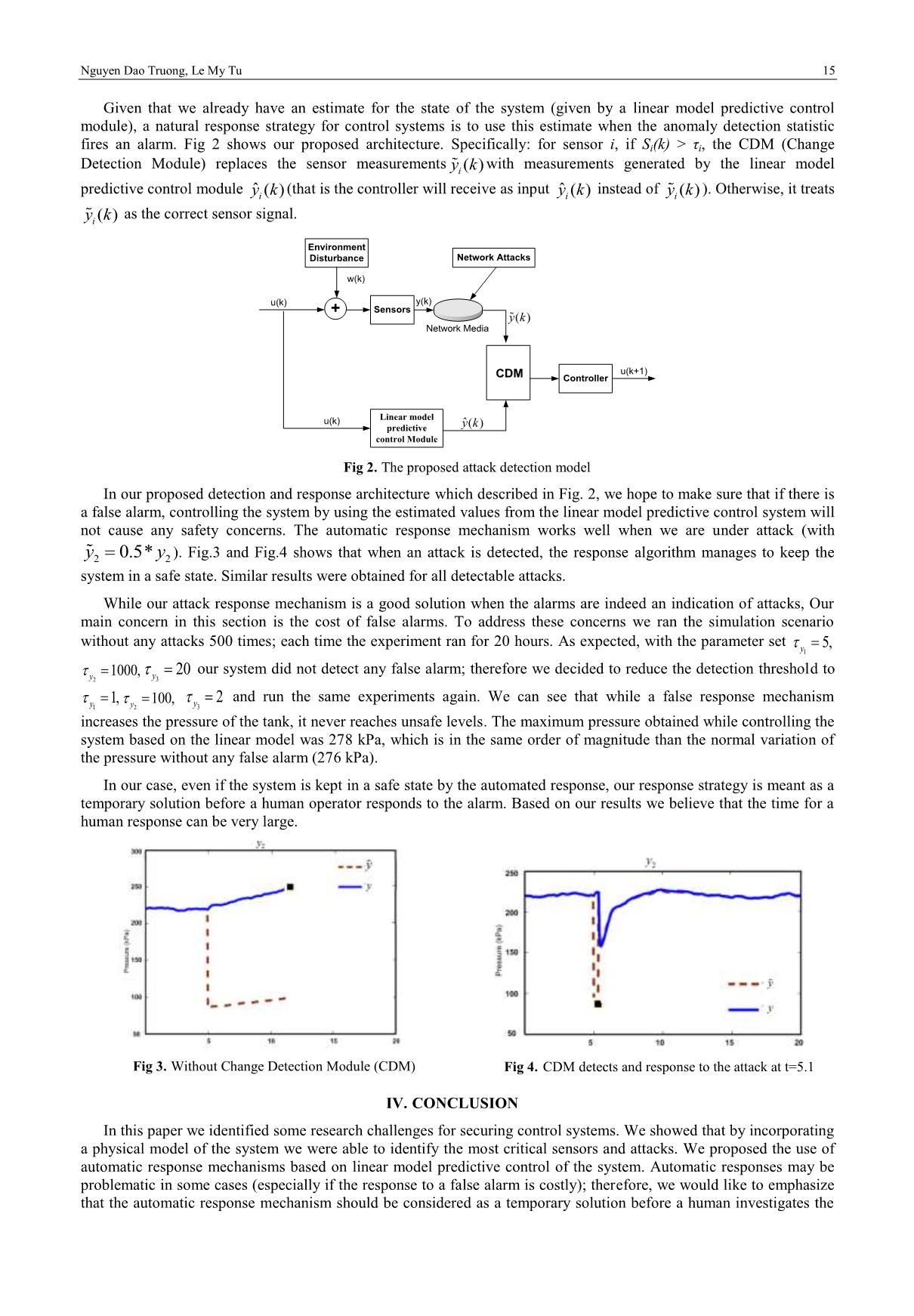
Given that we already have an estimate for the state of the system (given by a linear model predictive control 
module), a natural response strategy for control systems is to use this estimate when the anomaly detection statistic 
fires an alarm. Fig 2 shows our proposed architecture. Specifically: for sensor i, if Si(k) > τi, the CDM (Change 
Detection Module) replaces the sensor measurements ( )iy k with measurements generated by the linear model 
predictive control module ˆ ( )iy k (that is the controller will receive as input ˆ ( )iy k instead of ( )iy k ). Otherwise, it treats 
( )iy k as the correct sensor signal. 
Sensors+
Environment 
Disturbance Network Attacks
Controller
Linear model 
predictive 
control Module
u(k)
u(k+1)
w(k)
y(k)
u(k)
( )y k
ˆ( )y k
CDM
Network Media
Fig 2. The proposed attack detection model 
In our proposed detection and response architecture which described in Fig. 2, we hope to make sure that if there is 
a false alarm, controlling the system by using the estimated values from the linear model predictive control system will 
not cause any safety concerns. The automatic response mechanism works well when we are under attack (with 
2 20.5*y y ). Fig.3 and Fig.4 shows that when an attack is detected, the response algorithm manages to keep the 
system in a safe state. Similar results were obtained for all detectable attacks. 
While our attack response mechanism is a good solution when the alarms are indeed an indication of attacks, Our 
main concern in this section is the cost of false alarms. To address these concerns we ran the simulation scenario 
without any attacks 500 times; each time the experiment ran for 20 hours. As expected, with the parameter set 
1
5,y 
2
1000,y 3 20y our system did not detect any false alarm; therefore we decided to reduce the detection threshold to 
1
1,y 2 100,y 3 2y and run the same experiments again. We can see that while a false response mechanism 
increases the pressure of the tank, it never reaches unsafe levels. The maximum pressure obtained while controlling the 
system based on the linear model was 278 kPa, which is in the same order of magnitude than the normal variation of 
the pressure without any false alarm (276 kPa). 
In our case, even if the system is kept in a safe state by the automated response, our response strategy is meant as a 
temporary solution before a human operator responds to the alarm. Based on our results we believe that the time for a 
human response can be very large. 
Fig 3. Without Change Detection Module (CDM) 
Fig 4. CDM detects and response to the attack at t=5.1 
IV. CONCLUSION 
In this paper we identified some research challenges for securing control systems. We showed that by incorporating 
a physical model of the system we were able to identify the most critical sensors and attacks. We proposed the use of 
automatic response mechanisms based on linear model predictive control of the system. Automatic responses may be 
problematic in some cases (especially if the response to a false alarm is costly); therefore, we would like to emphasize 
that the automatic response mechanism should be considered as a temporary solution before a human investigates the 
16 A NEW METHOD AGAINST ATTACKS ON NETWORKED INDUSTRIAL CONTROL SYSTEMS 
alarm. A full deployment of any automatic response mechanism should take into consideration the amount of time in 
which it is reasonable for a human operator to respond, and the potential side effects of responding to a false alarm. 
However, as a word of caution, large scale control system designs are often not to resilient by design and may 
become prey to such stealth attacks if sufficient resilience is not built by design in the first place. Thus, our ideas 
become all the more relevant for operational security until there is a principled way of designing fully attack resilient 
control structures and algorithms (which by itself is a very challenging research endeavor and may not offer a cost 
effective design solution). By our proposed solution, we hope keep the system in safety state before the human 
operators can control the system and and no catastrophes occur. 
V. REFERENCES 
[1] Brodsky B. and Darkhovsky B., “Non-Parametric Methods in Change-Point Problems”, Kluwer Academic Publishers, 1993. 
[2] Clarke D. W., Mohtadi C and Tuffs P. S., “Generalized predictive control – Part I. The basic algorithm”, Automatica, 23: 137-
148, 1987. 
[3] Cutler C. R. and Ramker B. L. “Dynamic matrix control – a computer control algorithm”, Proceedings Joint Automatic Control 
Conference, Sanfrancisco, CA.,1980. 
[4] Denning D., “An intrusion-detection model”, Software Engineering, IEEE Transac- tions on SE-13(2), 1987, pp.222–232. 
[5] Eaton J. W., Rawlings J. B., “Model predictive control of chemical processes”, Chemical Engineering Science, 47: 705-720, 
1992. 
[6] Garcia C. E., Prett D. M., and Morari M., “Model predictive control: Theory and Practice - A survey”, Automatica, 25: 335-
348, 1989. 
[7] Goodwin G. C., Sin K. S., “Adaptive Filtering Prediction and Control”, Printice Hall, Englewood Cliffs, New Jersey, 1984. 
[8] Gu G., Zhang J. and Lee W., “Botsniffer: Detecting botnet command and control channels in network traffic”, in Proceedings 
of the 15th Annual Network and Distributed System Security Symposium (NDSS‟08), San Diego, CA, 2008. 
[9] Jung J., Paxson V., Berger A. and Balakrishan H., “Fast portscan detection using sequential hypothesis testing”, in Proceedings 
of the 2004 IEEE Symposium on Security and Privacy, 2004, pp. 211–225. 
[10] Kailath T. and Poor H. V., “Detection of stochastic processes”, IEEE Transactions on Information Theory 44(6), 1998, 
pp.2230–2258. 
[11] Quin S. J. and Badgwell T. A., “A survey of industrial model predictive control technology”, Control Engineering Practice 
11(7), 2003, pp.733-764. 
[12] Rawlings J., “Tutorial overview of model predictive control”, Control Systems Maga-zine, IEEE 20(3), 2000, pp.38–52. 
[13] Richalet J., Rault A., Testud J. L. and Papon J., “Model predictive heuristic control: Application to industrial processes”, 
Automatica, 14: 413-428, 1978. 
[14] Ricker N., “Model predictive control of a continuous, nonlinear, two-phase reactor”, Journal of Process Control 3(2), 1993, pp. 
109–123. 
[15] Schechter S. and Berger J. J. A., “Fast detection of scanning worm infections”, in „Proc. of the Seventh International 
Symposium on Recent Advances in Intrusion Detection (RAID)‟, 2004. 
[16] Venkateswarlu Ch., Gangiah K., “Constrained generalized predictive control of unstable nonlinear processes”, Transactions of 
Insitution of Chemical Engineers, 75: 371-376, 1997. 
[17] Venkateswarlu Ch., Naidu K.V.S. “Adaptive fuzzy model predictive control of an exothermic batch chemical reactor”, 
Chemical Engineering Communications, 186: 1-23, 2001. 
[18] Wald A., “Sequential Analysis”, J. Wiley & Sons, New York, NY, 1947. 
MỘT PHƯƠNG PHÁP MỚI CHỐNG TẤN CÔNG TRONG MẠNG 
ĐIỀU KHIỂN CÔNG NGHIỆP 
Nguyễn Đào Trường, Lê Mỹ Tú 
TÓM TẮT— Trong bài báo này, bằng cách kết hợp những kiến thức về điều khiển hệ thống vật lý, chúng tôi đề xuất một phương 
pháp mới để phát hiện các tấn công máy tính mà chúng làm thay đổi hành vi của hệ thống điều khiển công nghiệp. Bằng việc sử 
dụng những kiến thức về hệ thống vật lý chúng tôi tập trung vào phân tích các hình thức tấn công, những lỗ hổng bị khai thác không 
theo những cơ chế đặc thù mà từ đó kẻ tấn công có thể ẩn lấp. Chúng tôi phân tích sự an toàn của giải pháp đề xuất thông qua thực 
thi các hình thức tấn công và hy vọng giải pháp phản ứng tấn công tự động sẽ đưa hệ thống về trạng thái an toàn trước các tấn 
công. Trong bài báo này, chúng tôi đề xuất sử dụng hai module: một cho phát hiện những thay đổi bằng phương pháp phát hiện 
tuần tự và thống kê CUSUM, còn lại để phản ứng lại các tấn công bằng thuật toán điều khiển tiên đoán tuyến tính để giữ cho hệ 
thống ở trạng thái an toàn trước khi người vận hành có thể kiểm soát được tình hình.