Ước lượng VaR với tiếp cận Cornish - Fisher

TẠP CHÍ KHOA HỌC SỐ 4/2016 63 
 ƢỚC LƢỢNG VaR VỚI TIẾP CẬN CORNISH - FISHER 
 Trần Trọng Nguy n1(1), Nguyễn V n Tuấn1, Nguyễn Tiến Ninh2 
 1Học viện Chính sách và Phát triển 
 2Trường Đại học Sư phạm Hà Nội 2 
 Tóm tắt: Khi đo lường giá trị rủi ro của một tài sản, người ta thường sử dụng mô hình 
 VaR với giả thiết chuỗi lợi suất tài sản có phân phối chuẩn. Tuy nhiên, trong thực tế, giả 
 thiết phân phối chuẩn của lợi suất tài sản thường không thỏa mãn, đặc biệt đối với mẫu 
 nhỏ. Khi đó, rõ ràng các phương pháp ước lượng VaR truyền thống không còn chính xác 
 do sử dụng phân vị chuẩn. Trong bài báo này, chúng tôi giới thiệu phương pháp ước 
 lượng VaR với tiếp cận Cornish - Fisher bằng cách xấp xỉ giá trị phân vị chuẩn bởi khai 
 triển Taylor thông qua các hệ số nhọn và hệ số bất đối xứng. Kết quả thực nghiệm trên cổ 
 phiếu DST cho thấy mô hình khá tốt. Phương pháp này cũng có thể vận dụng trong đo 
 lường giá trị rủi ro của một danh mục đầu tư ở một hoặc nhiều lĩnh vực đầu tư tài chính 
 khác nhau. 
 Từ khóa: Mô hình VaR, kỹ thuật Cornish – Fisher, đo lường rủi ro 
1. MỞ ĐẦU 
 Đo lƣờng rủi ro thị trƣờng của các cổ phiếu đóng vai trò quan trọng trong quản trị rủi 
ro đầu tƣ chứng khoán. Việc nhận diện và đo lƣờng rủi ro của các cổ phiếu gi p nhà đầu tƣ 
cũng nhƣ cơ quan quản lý có những giải pháp phòng ngừa và hạn chế rủi ro. Trên thế giới 
đã có nhiều thƣớc đo rủi ro đƣợc khuyến nghị sử dụng trong đó thƣớc đo giá trị rủi ro 
(Value at Risk - ký hiệu VaR) nổi lên nhƣ một công cụ hữu hiệu nhất (xem [5], [6]). 
 Mô hình VaR (xem [5], [6]) thƣờng đƣợc sử dụng để đo lƣờng rủi ro thị trƣờng của 
một (hoặc danh mục đầu tƣ) tài sản. Trong mô hình này ngƣời ta giả thiết chuỗi lợi suất tài 
sản tuân theo quy luật phân phối chuẩn với trung bình μ và độ lệch chuẩn ζ nào đó. Khi đó, 
với mức tin cậy 1 - α, giá trị rủi ro của tài sản đƣợc tính theo công thức: 
1 Nhận bài ngày 20.04.2016; gửi phản biện và duyệt đăng ngày 10.05.2016 
 Liên hệ tác giả: Trần Trọng Nguyên; Email: nguyenttc@gmail.com 
64 TRƯỜNG ĐẠI HỌC THỦ ĐÔ HÀ NỘI 
 VaR  z  (1) 
trong đó zα là phân vị mức α của phân phối chuẩn hóa N(0,1). 
 Tuy nhiên, trong thực tế, giả thiết phân phối chuẩn của lợi suất tài sản thƣờng không 
thỏa mãn, đặc biệt đối với mẫu nhỏ. Khi đó, rõ ràng công thức tính VaR truyền thống ở 
trên không còn chính xác. Để giải quyết vấn đề này, ch ng tôi sử dụng phƣơng pháp 
Cornish - Fisher mở rộng bằng cách xấp xỉ giá trị phân vị chuẩn bởi khai triển Taylor 
thông qua các hệ số nhọn và hệ số bất đối xứng. 
 Cấu tr c bài báo nhƣ sau: Mục 2 giới thiệu ƣớc lƣợng VaR với kỹ thuật điều chỉnh 
Cornish – Fisher, mục 3 thử nghiệm đo lƣờng giá trị rủi ro VaR của cổ phiếu DST đang 
niêm yết trên Sở giao dịch chứng khoán Hà Nội, mục 4 là một số thảo luận. 
2. ƢỚC LƢỢNG VaR VỚI TIẾP CẬN CORNISH - FISHER 
2.1. Ƣớc lƣợng VaR truyền thống 
 Xét mô hình VaR đƣợc giới thiệu trong công thức (1). Với giả thiết chuỗi lợi suất {rt} 
phân phối chuẩn, ta dễ dàng xác định đƣợc phân vị chuẩn zα. Để ƣớc lƣợng VaR, ta cần 
ƣớc lƣợng các tham số μ và ζ của chuỗi lợi suất {rt}. Theo thời gian, có thể chuỗi lợi suất 
này không dừng, đặc biệt là phƣơng sai có thể không thuần nhất. Do đó ta phải xét lợi suất 
rt với điều kiện biết các thông tin tới thời điểm (t 1), nói cách khác ta phải xét chuỗi {rt} 
có điều kiện: (rt/Ft-1), trong đó Ft-1 là tập thông tin liên quan rt có đƣợc tới thời điểm (t 1). 
Khi đó, ngƣời ta thƣờng sử dụng hai phƣơng pháp sau để ƣớc lƣợng VaR. 
 Phƣơng pháp RiskMetricsTM 
 Năm 1995, ngân hàng JP Morgan đã đƣa ra phƣơng pháp RiskMetricsTM để ƣớc lƣợng 
VaR với các giả thiết cơ bản nhƣ sau: 
 1. Chuỗi lợi suất {rt} với điều kiện biết các thông tin tới thời điểm (t 1) có phân phối 
 2
chuẩn: (rt/Ft-1)  N(t,  t) 
 2. μt tuân theo mô hình ARMA(1,1). 
 2
 3. ζ t tuân theo mô hình GARCH (1,1). 
 Từ đó, nếu đặt ut = rt - μt thì: 
 2 2 2
 ut = tt với t  i.i.d.N(0,1) và  t = +  t-1 + (1 )u t-1. 
 Nhƣ vậy chuỗi {rt} tuân theo mô hình IGARCH (1,1). Trong thực tế tính toán, 
 TM
RiskMetrics cho μt 0 (xem [6]). 
 Phƣơng pháp toán kinh tế 
TẠP CHÍ KHOA HỌC SỐ 4/2016 65 
 Ta sử dụng lớp mô hình kinh tế lƣợng ARMA(m,n) mô tả lợi suất rt, mô hình 
 2
GARCH(p,q) mô tả phƣơng sai ζ t với các tham số m, n, p, q, phù hợp dạng: 
 mn
 rrti t i0 uu ti t i 
 ii 11
 ut = ζtεt 
 pq
 222
 tj t  jj0 t j  u 
 jj 11
 2
với εt ~i.i.d.N(0,ζ ). 
 Trong thực tế, ngƣời ta thƣờng lựa chọn các mô hình GARCH(1,1), GARCH(1,2), 
GARCH(2,1) cho phƣơng trình phƣơng sai. Ngoài ra có thể sử dụng một số dạng khác của 
mô hình GARCH nhƣ: IGARCH, MGARCH, EGARCH, TGARCH (xem [6]). 
 2.2. Ƣớc lƣợng VaR nhờ kỹ thuật Cornish-Fisher 
 Nhƣ đã giới thiệu ở trên, giả thiết phân phối chuẩn có vẻ là một giả thiết quá mạnh. 
Khi giả thiết chuẩn không thỏa mãn, ý tƣởng của Cornish – Fisher là sửa chữa các sai lệch 
phát sinh từ phân vị chuẩn bằng cách xấp xỉ bởi các moment của nó dựa trên khai triển 
chuỗi Taylor. Nói cách khác, phƣơng pháp này dựa trên đánh giá các moment của một 
phân bố sai lệch với đƣờng cong phân phối chuẩn để xác định các phân vị của phân bố này. 
 Phƣơng pháp Cornish - Fisher đƣợc phát triển bởi Cornish và Fisher (xem [3], [4]) để 
ƣớc lƣợng phân vị qα của một biến ngẫu nhiên dựa trên các moment của nó. Thông thƣờng, 
xấp xỉ Cornish – Fisher sử dụng 4 moment đầu tiên của phân phối nhƣ sau: 
 1 1 1
 qu ( u2 1)() EX 3 ( uuEX 3 3)() 4 (2 uuEX 3 5)() 3 2 
 6 24 36 
trong đó uα là phân vị mức α của phân phối chuẩn hóa N(0,1) (thƣờng ký hiệu là zα), 
E(X3) là hệ số bất đối xứng S và E(X4) là hệ số nhọn mở rộng (K-3) của phân phối. Công 
thức trên có thể viết lại nhƣ sau: 
 1 1 1
 q z ( z2 1)S ( z 3 3)(K3) z (2 z 3 5)S z 2 (2) 
 6 24 36 
 Từ đó có thể tính VaR của tài sản bởi công thức: 
 VaR  q  (3) 
 Trong thực nghiệm, các moment có thể ƣớc lƣợng thông qua mẫu dữ liệu lịch sử. Khi 
lợi suất có hệ số bất đối xứng đạt giá trị âm hay phần đuôi rộng (platykurtic) phƣơng pháp 
Cornish - Fisher sẽ đƣa một ƣớc lƣợng lớn hơn cho phần mất mát của VaR thông thƣờng. 
66 TRƯỜNG ĐẠI HỌC THỦ ĐÔ HÀ NỘI 
Ngƣợc lại, khi lợi suất có hệ số bất đối xứng dƣơng (leptokurtic), mức lỗ dự kiến sẽ nhỏ 
hơn của VaR thông thƣờng. Khi lợi suất phân phối chuẩn, các ƣớc lƣợng này hội tụ về các 
tham số của VaR thông thƣờng. 
3. ĐO LƢỜNG RỦI RO VaR BẰNG TIẾP CẬN CORNISH - FISHER 
 Trong mục này ch ng tôi thử nghiệm đo lƣờng giá trị rủi ro VaR của cổ phiếu DST 
(Công ty cổ phần sách và thiết bị giáo dục Nam Định) đang niêm yết trên Sở giao dịch 
chứng khoán Hà Nội. Việc phân tích dữ liệu và đo lƣờng VaR đƣợc thực hiện với sự hỗ trợ 
của các phần mềm Eviews, Excel... 
3.1. Phân tích số liệu 
 Thu thập dữ liệu về giá đóng cửa của cổ phiếu DST từ ngày 01/5/2015 đến ngày 
21/4/2016 với 321 phiên giao dịch (Nguồn: fpts.com.vn). Ch ng ta sẽ đo lƣờng rủi ro của 
cổ phiếu DST thông qua chuỗi lợi suất LS DST tƣơng ứng: 
 DSTtt DST 1
 LS_ RDSTt . 
 DSTt 1
 Trƣớc tiên, ta kiểm định tính chuẩn và tính dừng của chuỗi lợi suất này. Kết quả kiểm 
định đƣợc cho trong bảng 1 và bảng 2 sau đây. 
 Bảng 1. Kết quả kiểm định tính chuẩn của chuỗi lợi suất LS_DST 
 LS_DST 
 Jarque – Bera 147.4845 
 Probability 0.000000 
 Bảng 2. Kết quả kiểm định tính dừng của chuỗi lợi suất LS_DST 
 LS_DST 
 ADF Test Statistic 7.088784 
 1% Critical Value 3.4529 
 Từ các kết quả kiểm định trong bảng 1, với mức ý nghĩa rất nhỏ, theo tiêu chuẩn 
Jarque - Bera, chuỗi lợi suất LS DST không có phân phối chuẩn. Nhƣ vậy, không thể dùng 
công thức (1) để ƣớc lƣợng VaR của cổ phiếu này. Trong bảng 2, với mức ý nghĩa 1%, giá 
trị quan sát của thống kê Dickey - Fuller (ADF Test Statistic) có giá trị tuyệt đối lớn hơn 
giá trị tuyệt đối của mức tới hạn (Critical Value) tƣơng ứng, do đó có thể kết luận chuỗi lợi 
suất LS DST là chuỗi dừng. Điều này gợi ý rằng phân phối xác suất của chuỗi lợi suất 
TẠP CHÍ KHOA HỌC SỐ 4/2016 67 
LS DST có thể tuân theo một phân phối xác suất nào đó mà không phải phân phối chuẩn. 
Các phân tích này cho thấy, nên sử dụng kỹ thuật mở rộng Cornish - Fisher để ƣớc lƣợng 
giá trị rủi ro của cổ phiếu DST. 
 Tiếp theo, để lựa chọn mô hình chính xác cho ƣớc lƣợng VaR, ch ng ta kiểm tra lƣợc 
đồ tƣơng quan của chuỗi LS DST. Sử dụng phần mềm Eviews với chuỗi dữ liệu trên ta có 
lƣợc đồ sau: 
 Hình 1. Lƣợc đồ tƣơng quan của chuỗi LS_DST 
 Nhìn vào lƣợc đồ trên ta thấy lợi suất cổ phiếu DST phụ thuộc vào lợi suất của nó ở 1 
kỳ trƣớc. Từ đó, mô hình lựa chọn là AR(1) và MA(1). 
3.2. Ƣớc lƣợng VaR với tiếp cận Cornish-Fisher 
 Từ chuỗi số liệu về lợi suất cổ phiếu DST, ta ƣớc lƣợng đƣợc 2 hệ số nhọn và bất đối 
xứng tại thời điểm ngày 21/4/2016 là: S = - 0.135243, K = 6.314843. 
 Áp dụng kỹ thuật mở rộng của Cornish – Fisher, ta đƣa ra đƣợc các giá trị điều chỉnh 
của phân vị chuẩn với các mức ý nghĩa 5%; 2,5% và 1% nhƣ sau: 
 12 1 3 1 3 2
 q z ( z 1) S ( z 3)( z K 3) (2 z 5) z S (4) 
 6 24 36 
 Bảng 3. Kết quả tính qα tƣơng ứng với các mức ý nghĩa 
 5% 2.5% 1% 
 S K 
 zα qα zα qα zα qα 
68 TRƯỜNG ĐẠI HỌC THỦ ĐÔ HÀ NỘI 
 -0.135243 6.314843 -1.65 -1.616 -1.96 -2.2491 -2.33 -3.1938 
 Từ đó ta ƣớc lƣợng đƣợc VaR với tiếp cận Cornish – Fisher. Để so sánh, với mỗi 
phƣơng pháp ƣớc lƣợng VaR, ch ng tôi xét hai trƣờng hợp: giả thiết chuỗi lợi suất phân 
phối chuẩn và trƣờng hợp điều chỉnh bằng kỹ thuật của Cornish – Fisher. Kết quả thực 
nghiệm ƣớc lƣợng VaR tại thời điểm t = 322 (ngày 22/4/2016) với các mức ý nghĩa 5%, 
2,5% và 1% đƣợc tổng hợp trong bảng 4 và bảng 5. 
Bảng 4. Kết quả ƣớc lƣợng VaR bằng phƣơng pháp RickMetricsTM thông thƣờng v 
 phƣơng pháp RickMetricsTM với tiếp cận Cornish – Fisher 
 VaR 5% mVaR 5% VaR 2.5% mVaR 2.5% VaR 1% mVaR 1% 
 -0.04737 -0.04654 -0.05644 -0.06477 -0.06699 -0.09197 
 Bảng 5. Kết quả ƣớc lƣợng VaR bằng phƣơng pháp Toán kinh tế thông thƣờng v 
 phƣơng pháp Toán kinh tế với tiếp cận Cornish – Fisher 
 VaR 5% mVaR 5% VaR 2.5% mVaR 2.5% VaR 1% mVaR 1% 
 -0.04821 -0.04731 -0.05810 -0.04731 -0.06960 -0.09682 
3.3. Hậu kiểm mô hình VaR 
 Để đánh giá mức độ tin cậy của mô hình ch ng tôi tiến hành hậu kiểm mô hình theo 
các bƣớc sau: 
  Lấy dữ liệu giá đóng cửa của cổ phiếu DST trong 250 phiên giao dịch gần nhất; 
  Tính VaR bằng 2 phƣơng pháp trong cả hai trƣờng hợp: giả thiết chuỗi lợi suất 
phân phối chuẩn và trƣờng hợp điều chỉnh bằng kỹ thuật của Cornish – Fisher; 
  Tính Lãi – Lỗ (P&L) thực tế trong 250 phiên giao dịch đó; 
  Tính số lần P&L thực tế vƣợt ngƣỡng VaR của từng phƣơng pháp; 
  Kết luận: Trong 250 phiên quan sát, ở mức α = 5%, theo quy định của BIS (Bank 
of International Settlement Switzerland, [2]), nếu số lần P&L thực tế vƣợt ngƣỡng VaR 
không quá 19 thì mô hình đƣợc chấp nhận; tƣơng tự, số lần vƣợt ngƣỡng cho phép ở các 
mức 2,5% và 1% tƣơng ứng là 12 và 5. 
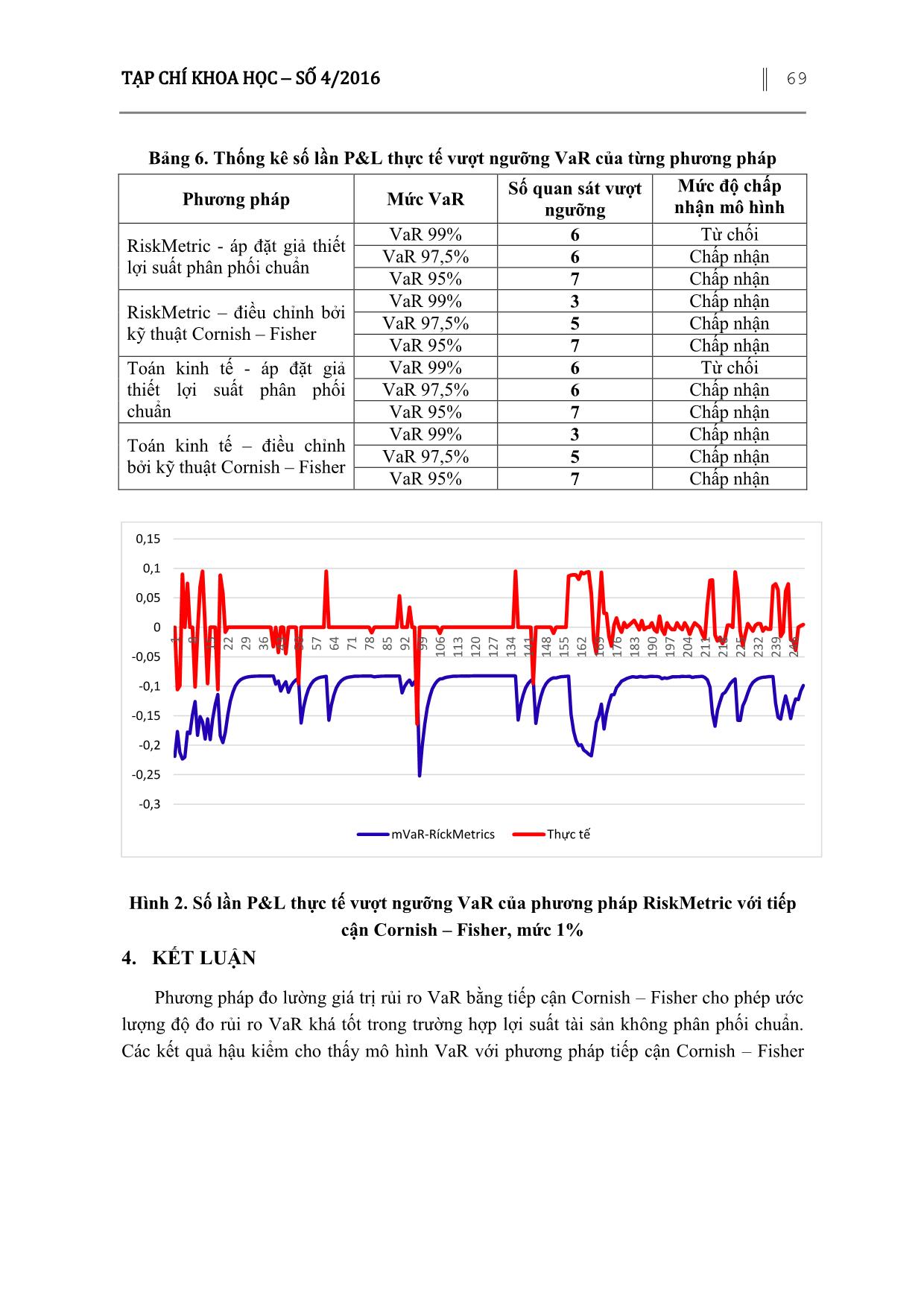
 Kết quả hậu kiểm các mô hình VaR cho cổ phiếu DST đƣợc cho trong bảng 6 và minh 
họa trong hình 2 sau đây. 
TẠP CHÍ KHOA HỌC SỐ 4/2016 69 
 Bảng 6. Thống k số lần P&L thực tế vƣợt ngƣỡng VaR của từng phƣơng pháp 
 Số quan sát vƣợt Mức độ chấp 
 Phƣơng pháp Mức VaR 
 ngƣỡng nhận mô hình 
 VaR 99% 6 Từ chối 
RiskMetric - áp đặt giả thiết 
 VaR 97,5% 6 Chấp nhận 
lợi suất phân phối chuẩn 
 VaR 95% 7 Chấp nhận 
 VaR 99% 3 Chấp nhận 
RiskMetric – điều chỉnh bởi 
 VaR 97,5% 5 Chấp nhận 
kỹ thuật Cornish – Fisher 
 VaR 95% 7 Chấp nhận 
Toán kinh tế - áp đặt giả VaR 99% 6 Từ chối 
thiết lợi suất phân phối VaR 97,5% 6 Chấp nhận 
chuẩn VaR 95% 7 Chấp nhận 
 VaR 99% 3 Chấp nhận 
Toán kinh tế – điều chỉnh 
 VaR 97,5% 5 Chấp nhận 
bởi kỹ thuật Cornish – Fisher 
 VaR 95% 7 Chấp nhận 
 0,15
 0,1
 0,05
 0
 1 8
 78 99
 15 22 29 36 43 50 57 64 71 85 92
 211
 113 120 127 134 141 148 155 162 169 176 183 190 197 204 218 225 232 239 246
 -0,05 106
 -0,1
 -0,15
 -0,2
 -0,25
 -0,3
 mVaR-RíckMetrics Thực tế 
Hình 2. Số lần P&L thực tế vƣợt ngƣỡng VaR của phƣơng pháp RiskMetric với tiếp 
 cận Cornish – Fisher, mức 1% 
4. KẾT LUẬN 
 Phƣơng pháp đo lƣờng giá trị rủi ro VaR bằng tiếp cận Cornish – Fisher cho phép ƣớc 
lƣợng độ đo rủi ro VaR khá tốt trong trƣờng hợp lợi suất tài sản không phân phối chuẩn. 
Các kết quả hậu kiểm cho thấy mô hình VaR với phƣơng pháp tiếp cận Cornish – Fisher 
70 TRƯỜNG ĐẠI HỌC THỦ ĐÔ HÀ NỘI 
đƣợc chấp nhận. Phƣơng pháp này cũng có thể vận dụng trong đo lƣờng giá trị rủi ro của 
một danh mục đầu tƣ trong một hoặc nhiều lĩnh vực đầu tƣ tài chính khác nhau. 
 TÀI LIỆU THAM KHẢO 
1. Angelidis, T., Benos, A., and Degiannakis, S. (2004), “The Use of GARCH Models in VaR 
 Estimation”, Statistical Methodology. 
2. Basel committee on Banking Supervision (1996), Amendment to the Capital Accord to 
 Incorporate Market Risks, Bank of International Settlement. Switzerland: Basel. 
3. Charles-Olivier Amédée-Manesme, Fabrice Barthélémy, Donald Keenan (2014), “Cornish-
 Fisher Expansion for Real Estate Value at Risk”, The Journal of Real Estate Finance and 
 Economics, May 2015, Volume 50, Issue 4, pp.439-464. 
4. Özlem Akta¸s and Maria Sjöstrand (2011), Cornish-Fisher Expansion and Value-at-Risk 
 method in application to risk management of large portfolios, Master‟s Thesis in Financial 
 Mathematics, School of Information Science, Computer and Electrical Engineering, Halmstad 
 University. 
5. Romain Berry (2008), Value-at-risk: An over view of analytical VaR, Investment analytics 
 and consulting, J.P.Morgan, USA, pp.7-9. 
6. Hoàng Đình Tuấn (2012), Mô hình phân tích và định giá tài sản tài chính, Nxb Đại học Kinh 
 tế Quốc dân. 
 ESTIMATE VAR WITH CORNISH-FISHER APPROACH 
 Abstract: When measure value at risk of an asset, one now usually used VaR model with 
 assume the distribution of the return rate is normally distribution. In fact, the distribution 
 of the return rate is usually not normally, especially with small samples. Therefore, the 
 methods to measure of VaR are no longer exactly because they were used normal 
 quantile. In this paper, we introduce an new approach to estimate of VaR by using 
 Cornish-Fisher expansion with its kurtosis coefficient and skewness coefficient. The 
 experiment with stock DST show that the model is well. This method can also be applied 
 when risk measurement in one or many fields financial investments deference. 
 Keywords: VaR model, Cornish-Fisher expansion, measure of risk