Ước lượng kênh và tối ưu chuỗi huấn luyện trong kênh truyền MIMO
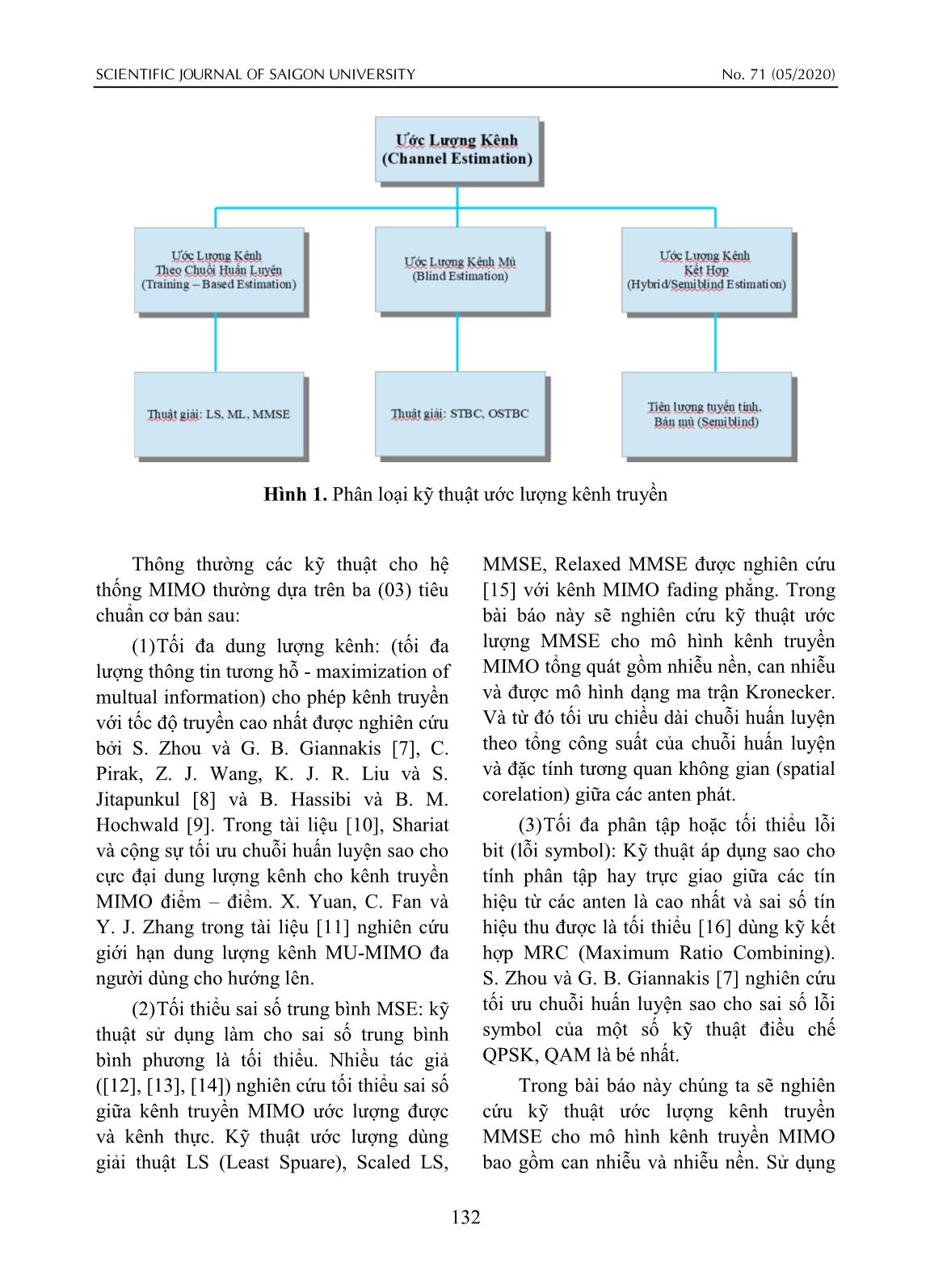
Trong hệ thống thông tin vô tuyến MIMO kỹ thuật ước lượng kênh truyền dựa vào chuỗi huấn luyện
luôn là vấn đề phức tạp và có nhiều phương pháp khác nhau. Trong bài báo này tối ưu chuỗi huấn luyện
bằng kỹ thuật ước lượng MMSE (Minimum Mean Square Error) cho mô hình kênh MIMO tổng quát
gồm nhiễu nền và can nhiễu dựa trên tiêu chuẩn tối thiểu sai số ước lượng trung bình MSE (Mean
Square Error). Bên cạnh đó, chiều dài trung bình chuỗi huấn luyện được tối ưu tùy theo đặc điểm thống
kê kênh truyền, tính tương quan của các anten phát và tổng công suất dùng cho chuỗi huấn luyện.

Trang 1

Trang 2
Trang 3

Trang 4

Trang 5

Trang 6

Trang 7
Trang 8
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Ước lượng kênh và tối ưu chuỗi huấn luyện trong kênh truyền MIMO", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
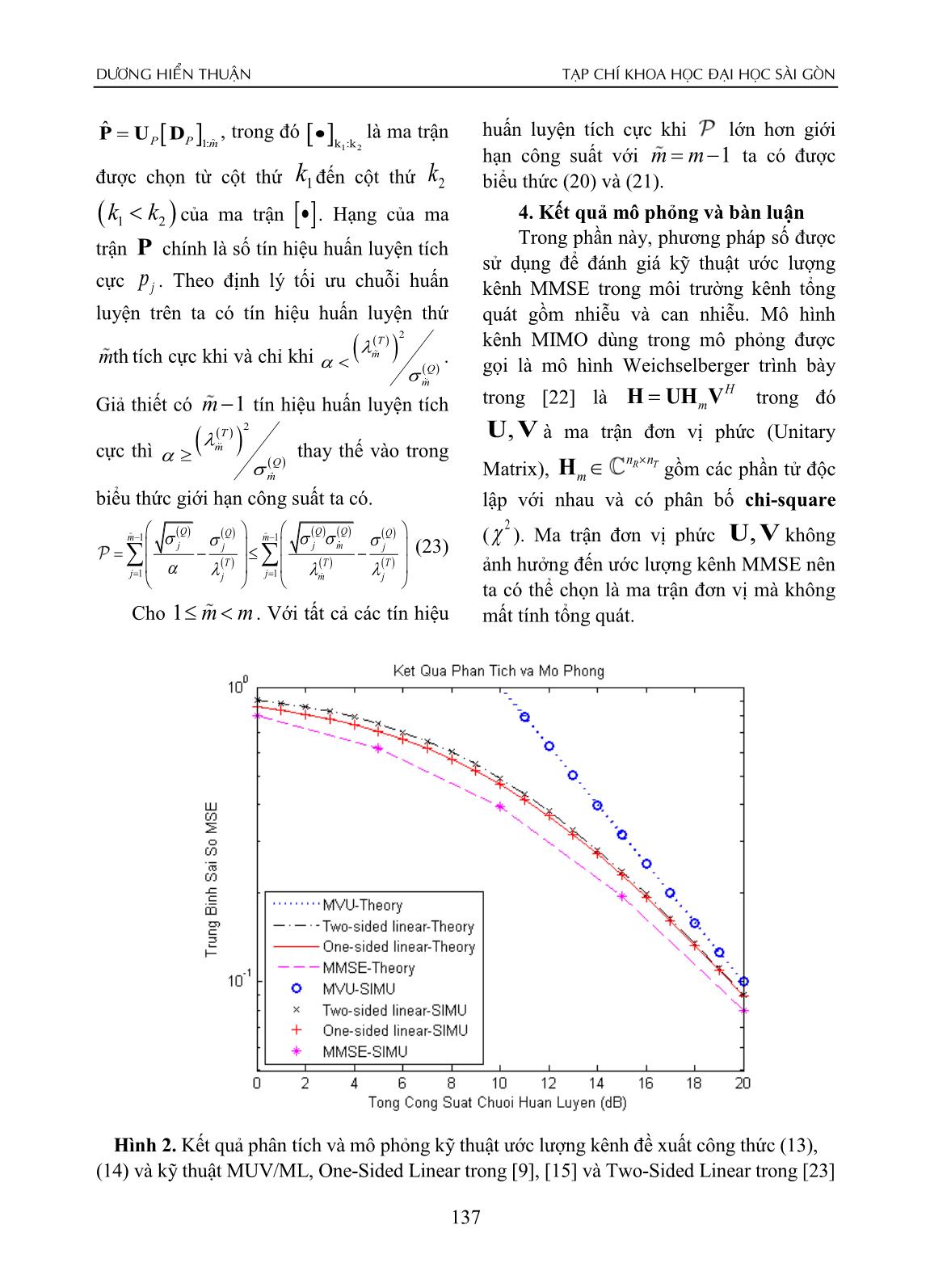
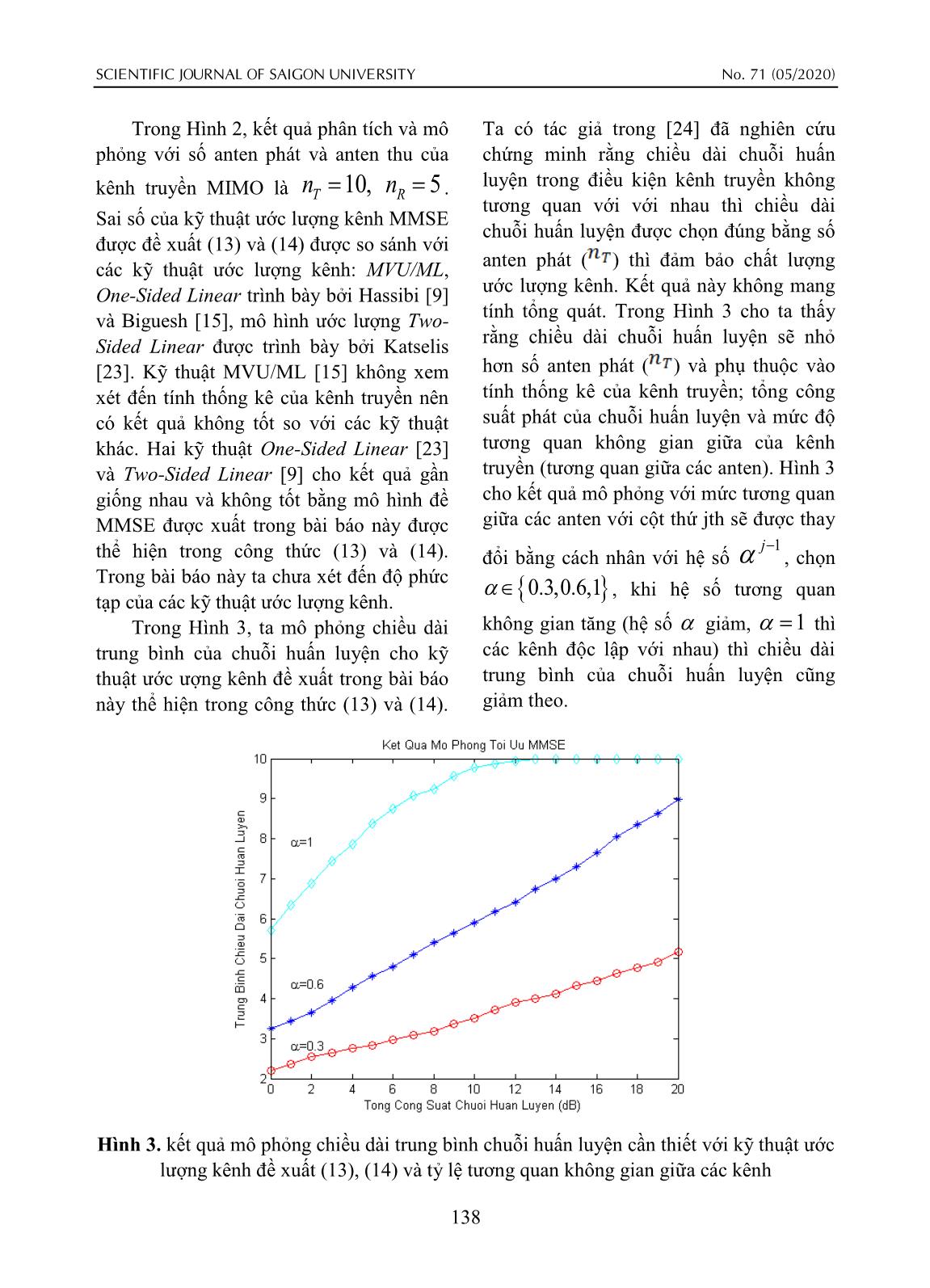
Tóm tắt nội dung tài liệu: Ước lượng kênh và tối ưu chuỗi huấn luyện trong kênh truyền MIMO

kênh MMSE sẽ là: Trong đó RT là ma trận ˆ 111 HH 1 nnRR vecvec HHRPMMSE S PP S d (6) phương sai không gian phát, RR 1 = vec HRPPRPSd HH là ma trận phương sai không gian thu, S là ma trận phương sai thời gian Trong đó: dYPHN vecvecvec - , Q (Do nhiễu nền và các can nhiễu), S là ma trận hiệp phương sai của nhiễu S nnRR là ma trận phương sai không nền và can nhiễu vec N và ma trận hiệp R phương sai lỗi: gian thu. H Bằng kỹ thuật phân tách theo giá trị CHHHHvec vecˆˆ vec vec MMSE MMSE MMSE (7) Eigen (Eigenvalue Decomposition) ta có: 11 R 11 PHHH S P R RP PRP S PR H H RUTTTT ΛU , RURRRR ΛU (11) Và chỉ số bình phương sai số ước H H lượng sẽ là SVQQQQ ΣV , SVRRRR ΣV (12) 2 MSE vec HHC vecˆ tr TT MMSE MMSE (8) Trong đó Λ diag ,..., Tn 1 T 11 tr R 11 PSPHHH tr RRPPRP SPR là ma trận đường chéo với các giá trị Eigen được sắp xếp giảm dần. Từ biểu thức ước lượng kênh truyền Σ diag QQ ,..., là ma trận đường (6) ta có bài toán tối ưu chuỗi huấn luyện Qn 1 T P sao cho việc việc sai số ước lượng kênh chéo với các giá trị Eigen được sắp 134 DƯƠNG HIỂN THUẬN TẠP CHÍ KHOA HỌC ĐẠI HỌC SÀI GÒN 1 RR MSEtr RRP TTT SPS1*1 xếp tăng dần. ΛRn diag 1 ,..., , TRQR T 1 (16) RR tr RRSPSP TTH 11 ΣRn diag 1 ,..., là ma trận đường RTRQ T 1 n chéo với các giá trị Eigen ngẫu nhiên. R 11 tr ΛUPVΣVPU 11HHH RR TTQQQT Định lý 1: Tối ưu công suất phân bố l 1 ll cho chuỗi huấn luyện với ước lượng kênh 11 MMSE: Đặt ab 0,0 và đặt jj RR Với mô hình kênh Kronecker ta phân ll H tách ma trận chuỗi huấn luyện theo giá trị P U P VTQ ta có (9) được viết lại riêng SVD (Sigular Value Decomposition), n R 1 H nT 11H PU TQΩV trong đó Ω có các MSEtrab min jTjQΛPΣP P (17) thành phần trên đường chéo chính là l 1 Subjecttotr PPH pp1 ,. . . , m giảm dần với pp1,. . . , m là 1 2 phân bố công suất cho chuỗi huấn luyện Đặt WPΣQ bằng phép khai triển lúc này sai số do ước lượng kênh tối thiểu SVD (Singular Value Decomposition) ta có (min) sẽ là: H thể biểu diễn WUDV WWW trong đó các TR m nnRT jl T (13) MSEtr R TR Rj giá trị Singular trong DW theo thứ tự giảm jlj 111 m jl 1 p 1 H j QR dần. Lúc này PΣPcủa biểu thức hàm jl Q Với phân bổ công suất như sau: mục tiêu trong (17) sẽ trở thành 1 HHH PΣPUDUDQWWWW và ta thấy ma QQ p max,0 jj (14) j T trận đơn vị phức (Unitary Matrix) VW j không ảnh hưởng đến giá trị của hàm mục Trong đó là hệ số Lagrange tiêu, một cách tổng quá ta có thể chọn (Lagrange Multiplier) được chọn sao cho VIW thì các phép toán vẫn không bị ảnh thỏa mãn điều kiện giới hạn công suất hưởng. Biểu thức giới hạn công suất trong m ta có (17) được biểu diễn lại: p j j 1 HH trPPWW tr ΣQ (18) 2 TRQR nR jljl Theo [19] thì biểu thức (18) được biểu 2 (15) QRTR l 1 p diễn lại như (19) và dấu bằng chỉ xảy ra khi jlj jl và chỉ khi phần tử trên đường chéo của Chứng minh: H WW và ΣQ có chiều tăng/giảm trái Từ mô hình kênh Kronecker (10) ta có ngược nhau: biểu thức MSE trong (9) được viết lại như sau: 135 SCIENTIFIC JOURNAL OF SAIGON UNIVERSITY No. 71 (05/2020) M H kênh thỏa mãn sai số cho phép. Theo định iMiQ WW 1 Σ (19) lý tối ưu ta có chiều dài chuỗi huấn luyện i 1 tối ưu bằng chính hạng của ma trận (rank) Trong đó là giá trị Eigen lớn thứ i. i P vì nếu r a n k()P thì ta cũng chỉ Từ việc đặt phân bố công suất của chuỗi huấn luyện 11 22HHtrên r a n k P kênh hữu dụng (được gọi là WPΣUDVUDIUDUPVQWWWWWWWTQQ Σ kênh hữu ích) còn lại -r ( )a n k P là kênh ta có thể chọn VIQ và lời giải tối ưu cho H không hữu dụng (được gọi là kênh vô ích). hàm mục tiêu (17) sẽ có dạng P U P T với Định lý 2: Tối ưu chiều dài chuỗi các phần tử trên đường chéo của P sắp huấn luyện (chính bằng hạng của ma trận theo thứ tự giảm dần cùng thứ tự với các chuỗi huấn luyện): 1 phần tử trên đường chéo của PΣ 2 . Q Với mô hình kênh Kronecker và Từ việc phân tích trên nếu đặt SI , RSRR thì ma trận chuỗi huấn luyện A abΛPΣP 11 H là kết hợp tuyến jjTjQ tối tưu MSE sẽ có hạng: N 1 tính nên tr A 1 là biểu thức lồi j rankmn P min, R khi và l 1 lj A chỉ khi 1 (Convex) theo [16] thì mintr A j đạt QQ m 1 Q 1 jm j được bằng tổng giá trị Eigen của ΛT cộng (20) TT 1 H j 1 mj với giá trị Eigen của PΣPQ với thứ tự ngược nhau. Như vậy với một P cho rankmm P nếu trước, ta sẽ giảm hàm mục tiêu trong (17) QQQQ QQ bằng cách loại bỏ các ma trận đơn vị phức mm 1 jmjm jj 1 (21) (Unitaty Matrix) thông qua phép biến đổi TTTT jj 11mjmj 1 SVD và sắp xếp các phần tử trên đường chéo và sau đó hiệu chỉnh (scaling) ma trận Chứng minh: còn lại cho phù hợp thực hiện đến khi điều Với mô hình kênh Kronecker và kiện giới hạn công suất thỏa mãn. Bằng , RSRR thì biểu thức tối ưu ước cách này tr A 1 sẽ là hàm lồi-Schur j lượng kênh (9) được viết lại. (Schur-Convex) áp dụng định lý 2.11 trong 1 11TTH [20] và tối ưu với điều kiện KKT trong MSE min tr RPISPI P (22) chương 5 của [21] ta có được biểu thức 1 1 HH T (13), (14) và (15). tr RUDDUI PPPP 3.3. Tối ưu chiều dài chuỗi huấn luyện Biểu thức trên không phụ thuộc vào HHHˆˆ Nhiệm vụ của việc tối ưu chuỗi huấn VP và ta có UPPPP D D U PP , Ước lượng luyện là tối ưu chiều dài của chuỗi huấn kênh tối ưu với ma trận chuỗi huấn luyện luyện sao cho vẫn đảm bảo việc ước lượng có hạng là m và được chọn là 136 DƯƠNG HIỂN THUẬN TẠP CHÍ KHOA HỌC ĐẠI HỌC SÀI GÒN Pˆ U D , trong đó là ma trận huấn luyện tích cực khi lớn hơn giới PP 1:m k : k 12 hạn công suất với mm 1 ta có được được chọn từ cột thứ k1 đến cột thứ k2 biểu thức (20) và (21). kk12 của ma trận . Hạng của ma 4. Kết quả mô phỏng và bàn luận Trong phần này, phương pháp số được trận P chính là số tín hiệu huấn luyện tích sử dụng để đánh giá kỹ thuật ước lượng cực p j . Theo định lý tối ưu chuỗi huấn kênh MMSE trong môi trường kênh tổng luyện trên ta có tín hiệu huấn luyện thứ quát gồm nhiễu và can nhiễu. Mô hình 2 T kênh MIMO dùng trong mô phỏng được mth tích cực khi và chỉ khi m . Q gọi là mô hình Weichselberger trình bày m H Giả thiết có m 1 tín hiệu huấn luyện tích trong [22] là H UHm V trong đó 2 T UV, à ma trận đơn vị phức (Unitary cực thì m thay thế vào trong Q nnRT m Matrix), Hm gồm các phần tử độc biểu thức giới hạn công suất ta có. lập với nhau và có phân bố chi-square 2 QQQ QQ mm 11 ( ). Ma trận đơn vị phức không jjm jj (23) TTT ảnh hưởng đến ước lượng kênh MMSE nên jj 11 jmj ta có thể chọn là ma trận đơn vị mà không Cho 1 mm. Với tất cả các tín hiệu mất tính tổng quát. Hình 2. Kết quả phân tích và mô phỏng kỹ thuật ước lượng kênh đề xuất công thức (13), (14) và kỹ thuật MUV/ML, One-Sided Linear trong [9], [15] và Two-Sided Linear trong [23] 137 SCIENTIFIC JOURNAL OF SAIGON UNIVERSITY No. 71 (05/2020) Trong Hình 2, kết quả phân tích và mô Ta có tác giả trong [24] đã nghiên cứu phỏng với số anten phát và anten thu của chứng minh rằng chiều dài chuỗi huấn luyện trong điều kiện kênh truyền không kênh truyền MIMO là nnTR 1 0 , 5 . tương quan với với nhau thì chiều dài Sai số của kỹ thuật ước lượng kênh MMSE chuỗi huấn luyện được chọn đúng bằng số được đề xuất (13) và (14) được so sánh với các kỹ thuật ước lượng kênh: MVU/ML, anten phát ( ) thì đảm bảo chất lượng One-Sided Linear trình bày bởi Hassibi [9] ước lượng kênh. Kết quả này không mang và Biguesh [15], mô hình ước lượng Two- tính tổng quát. Trong Hình 3 cho ta thấy Sided Linear được trình bày bởi Katselis rằng chiều dài chuỗi huấn luyện sẽ nhỏ [23]. Kỹ thuật MVU/ML [15] không xem hơn số anten phát ( ) và phụ thuộc vào xét đến tính thống kê của kênh truyền nên tính thống kê của kênh truyền; tổng công có kết quả không tốt so với các kỹ thuật suất phát của chuỗi huấn luyện và mức độ khác. Hai kỹ thuật One-Sided Linear [23] tương quan không gian giữa của kênh và Two-Sided Linear [9] cho kết quả gần truyền (tương quan giữa các anten). Hình 3 giống nhau và không tốt bằng mô hình đề cho kết quả mô phỏng với mức tương quan MMSE được xuất trong bài báo này được giữa các anten với cột thứ jth sẽ được thay j 1 thể hiện trong công thức (13) và (14). đổi bằng cách nhân với hệ số , chọn Trong bài báo này ta chưa xét đến độ phức 0.3,0.6,1 , khi hệ số tương quan tạp của các kỹ thuật ước lượng kênh. Trong Hình 3, ta mô phỏng chiều dài không gian tăng (hệ số giảm, 1 thì trung bình của chuỗi huấn luyện cho kỹ các kênh độc lập với nhau) thì chiều dài thuật ước ượng kênh đề xuất trong bài báo trung bình của chuỗi huấn luyện cũng này thể hiện trong công thức (13) và (14). giảm theo. Hình 3. kết quả mô phỏng chiều dài trung bình chuỗi huấn luyện cần thiết với kỹ thuật ước lượng kênh đề xuất (13), (14) và tỷ lệ tương quan không gian giữa các kênh 138 DƯƠNG HIỂN THUẬN TẠP CHÍ KHOA HỌC ĐẠI HỌC SÀI GÒN 5. Kết luận chiều dài của chuỗi huấn luyện cũng được Chuỗi huấn luyện được chọn tối ưu tối ưu dựa vào tổng công suất phát và đặc cho kênh truyền MIMO tổng quát (bao tính tương quan không gian giữa các anten gồm nhiễu nền và can nhiễu) thông qua với nhau. Ứng với một mức công suất thì giải thuật ước lượng kênh MMSE với tiêu tùy theo mức độ tương quan của tín hiệu chuẩn là tối thiểu bình phương sai số ước phát từ các anten mà chọn được chuỗi lượng cho kết quả tốt hơn so với các giải huấn luyện có chiều dài trung bình bé nhất thuật MUV/ML và giải thuật tuyến tính tiết kiệm tài nguyên của hệ thống mà vẫn trong các nghiên cứu trước. Kết quả cho đảm bảo tiêu chí đặt ra. Mức tương quan thấy kết quả mô phỏng tiệm cận với kết giữa các tín hiệu phát càng lớn (hệ số quả phân tích lý thuyết và với cùng một càng nhỏ) thì chiều dài trung bình chuỗi mức công suất cấp phát cho chuỗi huấn huấn luyện sẽ càng nhỏ. Khi mức các luyện thì kỹ thuật MMSE cho độ chính anten phát không tương quan với nhau tức xác cao nhất và bé hơn khoảng 1/10 (0.1) là hệ số 1 thì chiều dài trung bình so với các kỹ thuật MUV/ML và các kỹ chuỗi huấn luyện sẽ tiệm cận đến tổng số thuật tuyến tính khác. Ngoài ra trung bình lượng anten phát. TÀI LIỆU THAM KHẢO [1] METIS, (03/2020). “Mobile and wireless communications Enablers for Twenty- twenty (2020) Information Society”, [Online]. Available: https://metis2020.com/. [2] METIS, (03/2020). “Mobile and wireless communications Enablers for Twenty- twenty (2020) Information Society II”, [Online]. Available: https://metis-ii.5g- ppp.eu/. [3] P. Demestichas, A. Georgakopoulos, D. Karvounas, K. Tsagkaris and V. Stavroulaki, “5G on the Horizon: Key Challenges for the Radio-Access Network”, IEEE Vehicular Technology Magazine, 8(3), 47-53, 2013. [4] Q. C. Li, H. Niu, A. T. Papathanassiou and G. Wu, “5G Network Capacity: Key Elements and Technologies”, IEEE Vehicular Technology Magazine, 9(1), 71 – 78, 2014. [5] E. Telatar, “Capacity of Multi-Antenna Gaussian Channels”, European Transactions on Telecommunications, 10, 585-595, 1999. [6] R.S.Ganesh and J. Jayakumari, “Survey on Channel Estimation Techniques inMIMO-OFDM Mobile Communication Systems”, International Journal of Scientific & Engineering Research, 4(5), 1851-1855, 2013. [7] S. Zhou and G. B. Giannakis, “Optimal transmitter eigen-beamforming and space- time block coding based on channel correaltions”, IEEE Transactions on Information Theory, 49(7), 1673-1690, 2003. 139 SCIENTIFIC JOURNAL OF SAIGON UNIVERSITY No. 71 (05/2020) [8] C. Pirak, Z. J. Wang, K. J. R. Liu and S. Jitapunkul, “Optimum power allocation for maximum-likehood channel estimation in space-time coded MIMO Systems”, ICASSP'06, 2006. [9] B. Hassibi and B. Hochwald, “How much training is needed in multiple-antenna wireless links?”, IEEE Transactions on Information Theory, 49(4), 951-963, 2003. [10] M. H. Shariat, M. Biguesh and S. Gazor, “Optimal training sequence for wireless MIMO channel estimation”, 24th Biennial Symposium on Communications, Kingston, ON, 2008. [11] X. Yuan, C. Fan and Y. J. Zhang, “Fundamental Limits of Training-Based Uplink Multiuser MIMO Systems”, IEEE Transactions on Wireless Communications, 17(11), 7544-7558, 2018. [12] X. Ma, L. Yang and G. B. Giannakis, “Optimal training for MIMO frequency- selective fading channels”, IEEE Transactions on Wireless Communications, 4(2), 453-466, 2005. [13] T. L. Marzetta, “BLAST Training: Estimating Channel Characteristics for High Capacity Space-Time Wireless”, 37th Annual Allerton Conference on Communication, Control, and Computing, 1999. [14] J. Pang, J. Li, L. Zhao and Z. Lü, “Optimal training sequences for MIMO Chnanel Estimation with spatial correlation”, VTC-2007, 2007. [15] M. Biguesh and A. Gershman, “Training-based MIMO channel estimation: A study of estimator tradeoffs and optimal training signals”, IEEE Transactions on Signal Processing, 54(3), 884-893, 2006. [16] D. Brennan, "Linear diversity combining techniques," Proceedings of the IEEE, 91(2), 2003. [17] S. Kay, Fundamentals of Statistical Signal Processing: Estimation Theory, NJ: Prentice Hall, 1993. [18] Y. Liu, T. Wong and W. Hager, “Training signal design for estimation of correlated MIMO channels with colored interference”. IEEE Transactions on Signal Processing, 55(4), 1486-1497, 2007. [19] A. Marshall and I. Olkin, Inequalities: Theory of Majorization and Its Applications, New York Academic Press, 1979. [20] E. Jorswieck and H. Boche, Majorization and matrix-monotone functions in wireless communications, Now Publishers Inc, 2007. [21] S. Boyd and L. Vandenberghe, Convex Optimization, Cambridge University Press, 2004. 140 DƯƠNG HIỂN THUẬN TẠP CHÍ KHOA HỌC ĐẠI HỌC SÀI GÒN [22] W. Weichselberger, M. Herdin, H. Özcelik and a. E. Bonek, “A stochastic MIMO channel model with joint correlation of both link ends”, IEEE Transactions on Wireless Communications, 50(1), 90-100, 2006. [23] D. Katselis, E. Kofidis and S. Theodoridis, “On training optimization for estimation of correlated MIMO channels in the presence of multiuser interference”, IEEE Transactions on Signal Processing, 56(10), 4892-4904, 2008. [24] B. H. a. B. M. Hochwald, “How much training is needed in multiple-antenna wireless links?”, IEEE Transactions on Information Theory, 49(4), 951-963, 2003. [25] X. Yuan, C. Fan and Y. J. Zhang, “Fundamental Limits of Training-Based Uplink Multiuser MIMO Systems”, IEEE Transactions on Wireless Communications, 17(11), 7544-7558, 2018. Ngày nhận bài: 08/4/2020 Biên tập xong: 15/5/2020 Duyệt đăng: 20/5/2020 141
File đính kèm:
 uoc_luong_kenh_va_toi_uu_chuoi_huan_luyen_trong_kenh_truyen.pdf
uoc_luong_kenh_va_toi_uu_chuoi_huan_luyen_trong_kenh_truyen.pdf

