Ứng dụng phương trình trạng thái trong chính xác hóa phân bố đặc tính chất lưu cho vỉa dầu có động thái lưu biến phức tạp

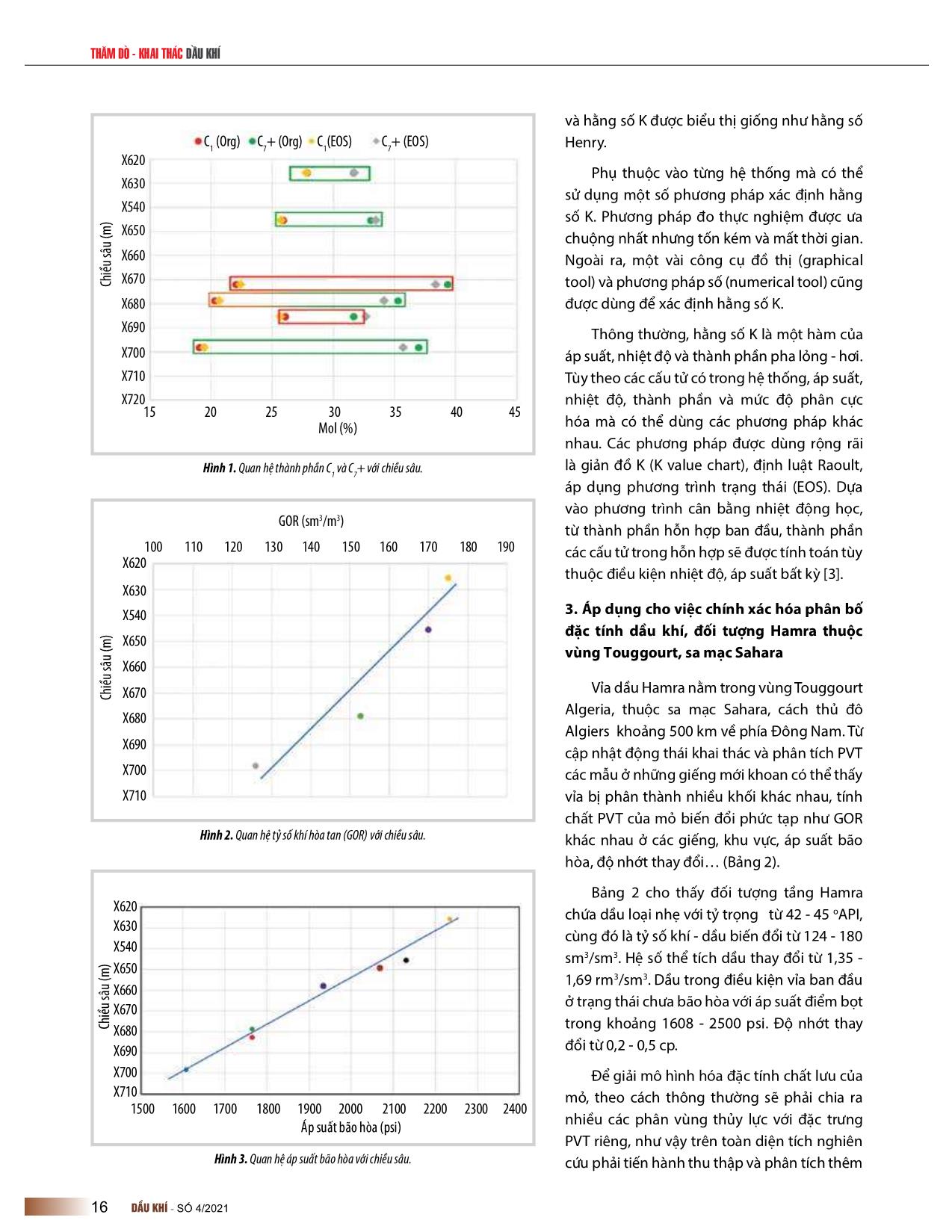
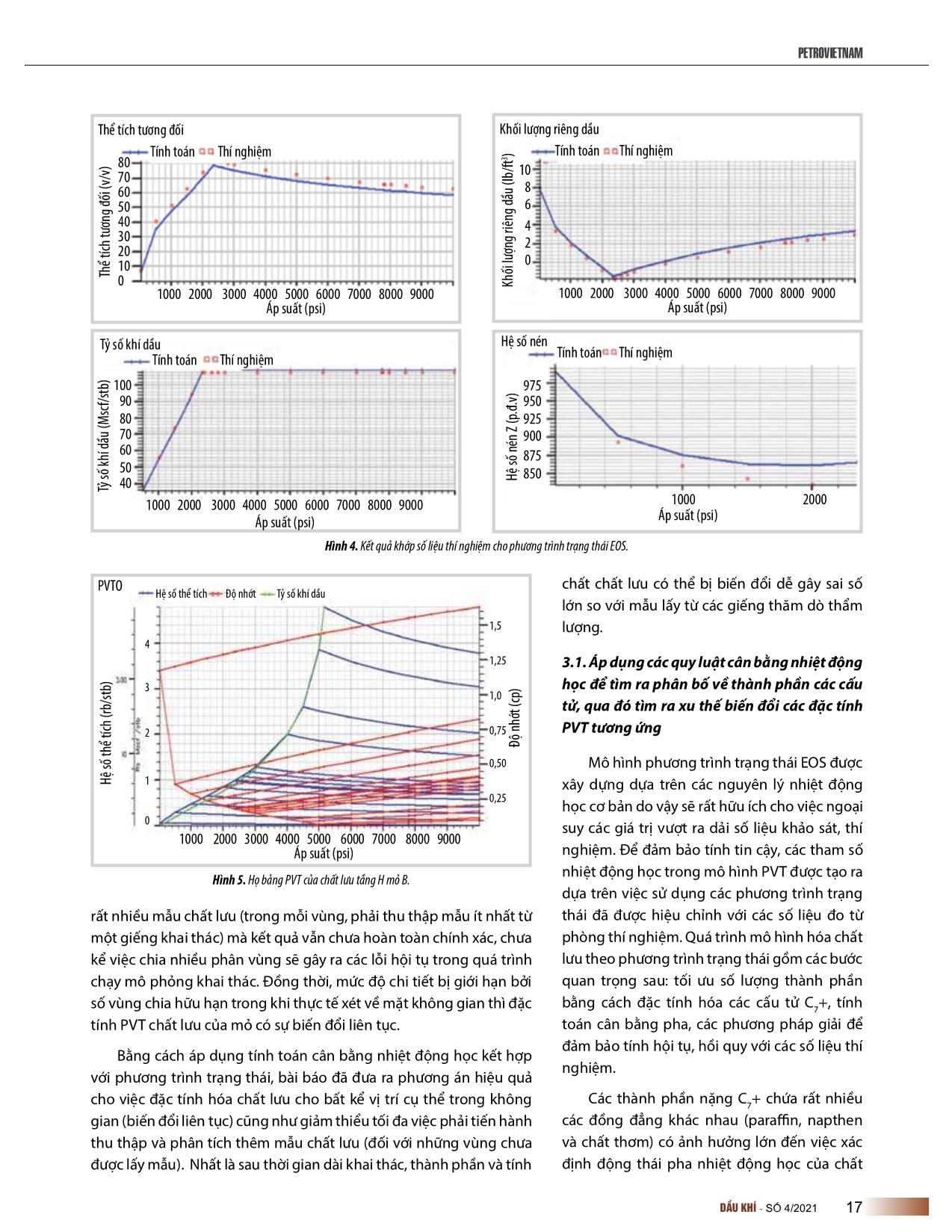
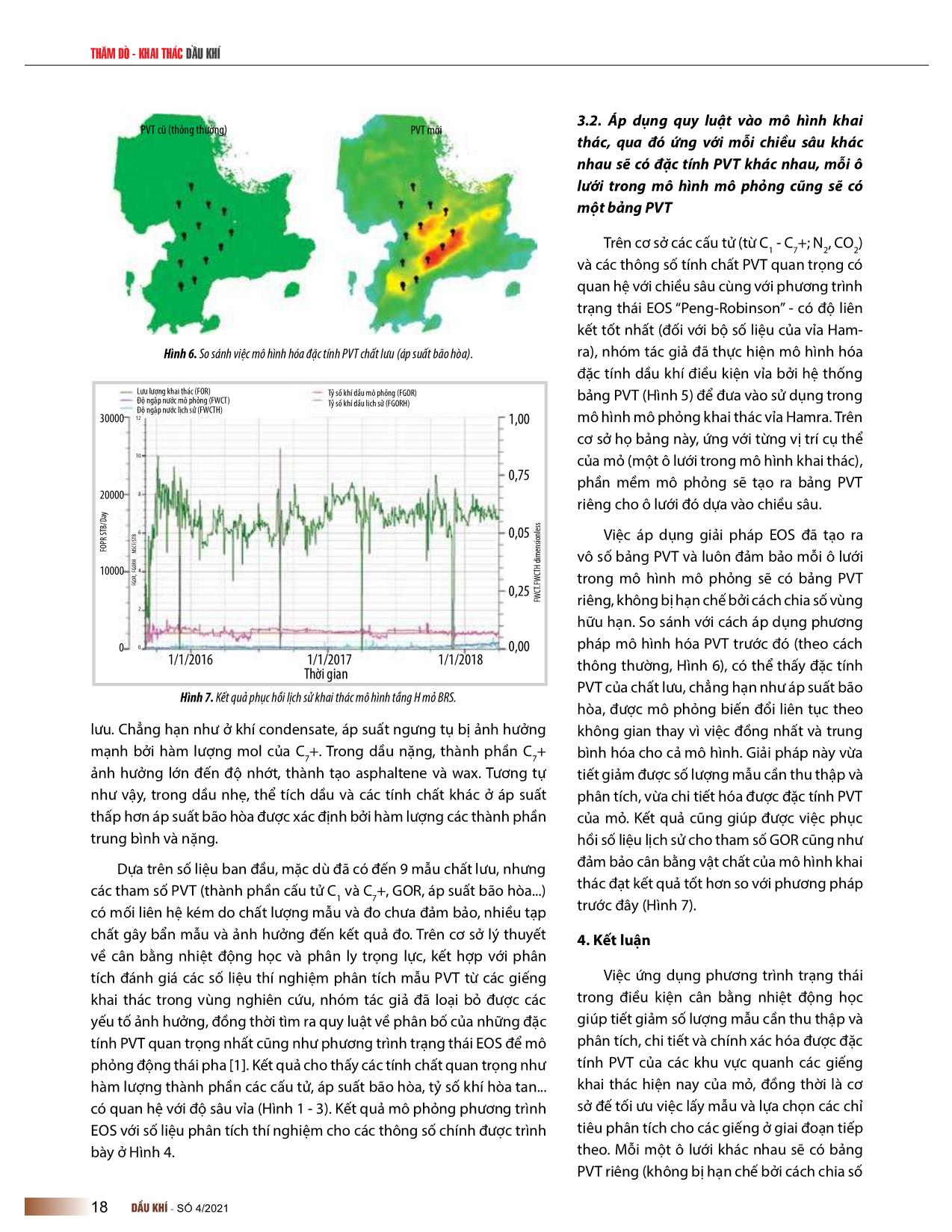
t 
 thái (EOS) [1]. Bắt đầu từ định luật Boyle - Charles sử 
 dụng cho khí lý tưởng biểu thị bằng công thức sau :
 Ngày nhận bài: 1/3/2021. Ngày phản biện đánh giá và sửa chữa: 1 - 24/3/2021.  (1)
 Ngày bài báo được duyệt đăng: 1/4/2021.
14 DẦUKHÍSỐ4/2021
 
 Trong đó: chính xác của phương trình trạng thái trong việc dự đoán cân bằng 
 pha, tính áp suất hơi, tỷ trọng lỏng, tỷ trọng khí, tỷ lệ các pha cân 
 P: Áp suất (psia)
 bằng
 V: Thể tích (ft3)
 Bảng 1. Các phương trình trạng thái EOS phổ biến trong công nghiệp dầu khí
 n: Số mol khí ở điều kiện áp suất P, nhiệt 
 ( )
độ T có thể tích V (mol) Peng - Robinson (PR) (1976) 
 [ ( + ) + ( − )]
 T: Nhiệt độ (oR)
 ( )
 Fuller (1976) 
 R: Hằng số khí, R = 10,732 (psia.scf/lb. mol. ( + )
o
R). ( )
 Heyen (1980) (Sandler, 1994)
 Ban đầu, EOS (1) chỉ được áp dụng chủ yếu [ + ( ( ) + ) − ( ) ] 
cho các cấu tử tinh khiết, sau đó được phát ( )
 Schmit - Wenzel (1980) 
triển cho các hợp chất nhiều thành phần hơn. ()+ + 
Khi mới áp dụng cho hỗn hợp, chúng được ( )
 Kubic (1982) 
dùng đối với các hỗn hợp không phân cực ( + ) 
(các EOS: Soave (1972); Peng and Robinson ( )
 Adachi (1983) 
(1976) và các hợp chất phân cực yếu (các EOS: [( − )( + )]
Huron (1978); Assenlineau (1978); Graboski 
 ( )
và Daubert (1978)) [1]. Sau đó, phương trình Stryjeck - Vera (SV) (1986) 
 ( + 2 − ) 
trạng thái đã phát triển nhanh chóng cho việc 
 ( )
tính toán đặc tính chất lưu PVT của các hỗn Schwartzentruber - Renon (1989) 
 [( + )( + 2 + )]
hợp cả phân cực và không phân cực.
 Có nhiều điểm thuận tiện cho việc áp Trong đó:
dụng phương trình trạng thái trong việc a, b, c: Hệ số tương quan được tính toán theo áp suất tới hạn và 
tính toán đặc tính chất lưu: i) dùng được với nhiệt độ tới hạn;
khoảng áp suất và nhiệt độ rộng, kể cả vùng 
áp suất cao; ii) các cấu tử có thể thay đổi bất kỳ, w: Hệ số lệch cầu.
từ nhẹ tới nặng, từ không phân cực tới phân 2.2. Cân bằng nhiệt động học
cực; iii) có thể dùng cho cân bằng lỏng - hơi, 
lỏng - lỏng; iv) có thể dùng cho cả pha hơi và Cân bằng nhiệt động giữa lỏng và hơi của cấu tử i được biểu thị 
pha lỏng. Ngoài ra, các phương trình trạng như sau [2]:
thái còn dùng để xác định các tính chất như tỷ V L (2)
 f i = f i 
trọng, áp suất hơi, enthalpy, entropy
 Trong đó: V , L là độ bay hơi của cấu tử i trong pha hơi và pha 
 f i f i
 Phương trình Van Der Waals là phương lỏng.
trình trạng thái đầu tiên dự đoán sự cùng tồn 
tại 2 pha lỏng - hơi. Sau đó, Redlich - Kwong Tuy nhiên, trong thực tế, thường sử dụng phương trình sau:
(1949), Soave (1972) và Peng Robinson (1976), K =  (3)
 
Carhanan và Starling (1969), Guggenheim 
(1965) và Boublik (1981), Chen và Kreglewski Ki được gọi là hằng số cân bằng pha lỏng - hơi của cấu tử i, bằng 
(1977), Christoforakos và Franck (1986), Heilig tỷ lệ giữa phần mol của cấu tử i trong pha hơi (yi) và phần mol của nó 
và Franck (1989) [1] lần lượt cải tiến để tăng độ trong pha lỏng (xi). Phương trình này còn được gọi là Định luật Henry 
 Bảng 2. Tóm tắt các đặc tính dầu - khí từ các giếng khai thác vỉa Hamra
 Mẫu A B C D E F G 
 Chiều sâu (mTVD) x630 x622 x407 x460 x421 x029 x683 
 Tỷ số khí dầu (sm3/sm3) 174 126 175 170 178 180 124 
 Áp suất bão hòa (psi) 2340 1608 2234 2130 2123 2500 2021 
 Hệ số thể tích (rm3/sm3) 1,609 1,610 1,605 1,631 1,691 1,397 1,356 
 Tỷ trọng (API) 42,1 43,8 42,8 42,9 42,0 44,1 44,8 
 DẦUKHÍSỐ4/2021 15
THĂMDÒ-KHAITHÁCDẦUKHÍ
 và hằng số K được biểu thị giống như hằng số 
 C1 (Org) C7+ (Org) C1(EOS) C7+ (EOS) Henry.
 X620
 Phụ thuộc vào từng hệ thống mà có thể 
 X630
 sử dụng một số phương pháp xác định hằng 
 X540
 số K. Phương pháp đo thực nghiệm được ưa 
 X650
 chuộng nhất nhưng tốn kém và mất thời gian. 
 X660 Ngoài ra, một vài công cụ đồ thị (graphical 
 Chiều sâu (m) Chiều X670 tool) và phương pháp số (numerical tool) cũng 
 X680 được dùng để xác định hằng số K.
 X690 Thông thường, hằng số K là một hàm của 
 X700 áp suất, nhiệt độ và thành phần pha lỏng - hơi. 
 X710 Tùy theo các cấu tử có trong hệ thống, áp suất, 
 X720 nhiệt độ, thành phần và mức độ phân cực 
 15 20 25 30 35 40 45 
 Mol (%) hóa mà có thể dùng các phương pháp khác 
 nhau. Các phương pháp được dùng rộng rãi 
 là giản đồ K (K value chart), định luật Raoult, 
 Hình 1. Quan hệ thành phần C1 và C7+ với chiều sâu.
 áp dụng phương trình trạng thái (EOS). Dựa 
 vào phương trình cân bằng nhiệt động học, 
 GOR (sm3/m3)
 từ thành phần hỗn hợp ban đầu, thành phần 
 100 110 120 130 140 150 160 170 180 190 các cấu tử trong hỗn hợp sẽ được tính toán tùy 
 X620
 thuộc điều kiện nhiệt độ, áp suất bất kỳ [3].
 X630
 X540 3. Áp dụng cho việc chính xác hóa phân bố 
 đặc tính dầu khí, đối tượng Hamra thuộc 
 X650
 vùng Touggourt, sa mạc Sahara
 X660
 Vỉa dầu Hamra nằm trong vùng Touggourt 
 Chiều sâu Chiều (m) X670
 Algeria, thuộc sa mạc Sahara, cách thủ đô 
 X680
 Algiers khoảng 500 km về phía Đông Nam. Từ 
 X690
 cập nhật động thái khai thác và phân tích PVT 
 X700 các mẫu ở những giếng mới khoan có thể thấy 
 X710 vỉa bị phân thành nhiều khối khác nhau, tính 
 chất PVT của mỏ biến đổi phức tạp như GOR 
 Hình 2. Quan hệ tỷ số khí hòa tan (GOR) với chiều sâu. khác nhau ở các giếng, khu vực, áp suất bão 
 hòa, độ nhớt thay đổi (Bảng 2). 
 Bảng 2 cho thấy đối tượng tầng Hamra 
 X620
 chứa dầu loại nhẹ với tỷ trọng từ 42 - 45 oAPI, 
 X630
 cùng đó là tỷ số khí - dầu biến đổi từ 124 - 180 
 X540
 sm3/sm3. Hệ số thể tích dầu thay đổi từ 1,35 - 
 X650
 1,69 rm3/sm3. Dầu trong điều kiện vỉa ban đầu 
 X660
 ở trạng thái chưa bão hòa với áp suất điểm bọt 
 X670
 Chiều sâu (m) Chiều X680 trong khoảng 1608 - 2500 psi. Độ nhớt thay 
 X690 đổi từ 0,2 - 0,5 cp.
 X700 Để giải mô hình hóa đặc tính chất lưu của 
 X710 mỏ, theo cách thông thường sẽ phải chia ra 
 1500 1600 1700 1800 1900 2000 2100 2200 2300 2400
 nhiều các phân vùng thủy lực với đặc trưng 
 Áp suất bão hòa (psi)
 PVT riêng, như vậy trên toàn diện tích nghiên 
 Hình 3. Quan hệ áp suất bão hòa với chiều sâu. cứu phải tiến hành thu thập và phân tích thêm 
16 DẦUKHÍSỐ4/2021
 
 Thể tích tương đối Khối lượng riêng dầu
 Tính toán Thí nghiệm ) Tính toán Thí nghiệm
 80 3
 70 10
 60 8
 50 6
 40 4
 30 2
 20
 10 0
 Thể (v/v) tích đối tương Thể
 0 Khốiriêng(Ib/ft lượng dầu
 1000 2000 3000 4000 5000 6000 7000 8000 9000 1000 2000 3000 4000 5000 6000 7000 8000 9000 
 Áp suất (psi) Áp suất (psi)
 Tỷ số khí dầu Hệ số nén
 Tính toán Thí nghiệm Tính toán Thí nghiệm
 100 975
 90 950
 80 925
 70 900
 60 875
 50
 Hệ số nén Z Hệ (p.đ.v) số nén 850
 40
 Tỷ sốkhí (Mscf/stb) dầu Tỷ
 1000 2000 3000 4000 5000 6000 7000 8000 9000 1000 2000 
 Áp suất (psi) Áp suất (psi)
 Hình 4. Kết quả khớp số liệu thí nghiệm cho phương trình trạng thái EOS.
 chất chất lưu có thể bị biến đổi dễ gây sai số 
 PVTO Hệ số thể tích Độ nhớt Tỷ số khí dầu
 lớn so với mẫu lấy từ các giếng thăm dò thẩm 
 1,5 lượng.
 4
 1,25 3.1. Áp dụng các quy luật cân bằng nhiệt động 
 3 học để tìm ra phân bố về thành phần các cấu 
 1,0
 tử, qua đó tìm ra xu thế biến đổi các đặc tính 
 2 0,75 PVT tương ứng
 Độ nhớt (cp) Độ(cp) nhớt 
 0,50 Mô hình phương trình trạng thái EOS được 
 Hệ số thể tích Hệ (rb/stb)thể tích số 1 xây dựng dựa trên các nguyên lý nhiệt động 
 0,25
 học cơ bản do vậy sẽ rất hữu ích cho việc ngoại 
 0
 suy các giá trị vượt ra dải số liệu khảo sát, thí 
 1000 2000 3000 4000 5000 6000 7000 8000 9000 
 Áp suất (psi) nghiệm. Để đảm bảo tính tin cậy, các tham số 
 nhiệt động học trong mô hình PVT được tạo ra 
 Hình 5. Họ bảng PVT của chất lưu tầng H mỏ B.
 dựa trên việc sử dụng các phương trình trạng 
rất nhiều mẫu chất lưu (trong mỗi vùng, phải thu thập mẫu ít nhất từ thái đã được hiệu chỉnh với các số liệu đo từ 
một giếng khai thác) mà kết quả vẫn chưa hoàn toàn chính xác, chưa phòng thí nghiệm. Quá trình mô hình hóa chất 
kể việc chia nhiều phân vùng sẽ gây ra các lỗi hội tụ trong quá trình lưu theo phương trình trạng thái gồm các bước 
chạy mô phỏng khai thác. Đồng thời, mức độ chi tiết bị giới hạn bởi quan trọng sau: tối ưu số lượng thành phần 
số vùng chia hữu hạn trong khi thực tế xét về mặt không gian thì đặc bằng cách đặc tính hóa các cấu tử C7+, tính 
tính PVT chất lưu của mỏ có sự biến đổi liên tục. toán cân bằng pha, các phương pháp giải để 
 đảm bảo tính hội tụ, hồi quy với các số liệu thí 
 Bằng cách áp dụng tính toán cân bằng nhiệt động học kết hợp 
 nghiệm.
với phương trình trạng thái, bài báo đã đưa ra phương án hiệu quả 
cho việc đặc tính hóa chất lưu cho bất kể vị trí cụ thể trong không Các thành phần nặng C7+ chứa rất nhiều 
gian (biến đổi liên tục) cũng như giảm thiểu tối đa việc phải tiến hành các đồng đẳng khác nhau (paran, napthen 
thu thập và phân tích thêm mẫu chất lưu (đối với những vùng chưa và chất thơm) có ảnh hưởng lớn đến việc xác 
được lấy mẫu). Nhất là sau thời gian dài khai thác, thành phần và tính định động thái pha nhiệt động học của chất 
 DẦUKHÍSỐ4/2021 17
THĂMDÒ-KHAITHÁCDẦUKHÍ
 3.2. Áp dụng quy luật vào mô hình khai 
 PVT cũ (thông thường) PVT mới
 thác, qua đó ứng với mỗi chiều sâu khác 
 nhau sẽ có đặc tính PVT khác nhau, mỗi ô 
 lưới trong mô hình mô phỏng cũng sẽ có 
 một bảng PVT
 Trên cơ sở các cấu tử (từ C1 - C7+; N2, CO2) 
 và các thông số tính chất PVT quan trọng có 
 quan hệ với chiều sâu cùng với phương trình 
 trạng thái EOS “Peng-Robinson” - có độ liên 
 kết tốt nhất (đối với bộ số liệu của vỉa Ham-
 Hình 6. So sánh việc mô hình hóa đặc tính PVT chất lưu (áp suất bão hòa). ra), nhóm tác giả đã thực hiện mô hình hóa 
 đặc tính dầu khí điều kiện vỉa bởi hệ thống 
 Lưu lượng khai thác (FOR) Tỷ số khí dầu mô phỏng (FGOR)
 Độ ngập nước mô phỏng (FWCT) Tỷ số khí dầu lịch sử (FGORH) bảng PVT (Hình 5) để đưa vào sử dụng trong 
 Độ ngập nước lịch sử (FWCTH)
 30000 12 1,00 mô hình mô phỏng khai thác vỉa Hamra. Trên 
 cơ sở họ bảng này, ứng với từng vị trí cụ thể 
 10 của mỏ (một ô lưới trong mô hình khai thác), 
 0,75 phần mềm mô phỏng sẽ tạo ra bảng PVT 
 20000 8
 riêng cho ô lưới đó dựa vào chiều sâu.
 6 0,05 Việc áp dụng giải pháp EOS đã tạo ra 
 FOPR FOPR STB/Day vô số bảng PVT và luôn đảm bảo mỗi ô lưới 
 10000 4
 FGOR, FGORH FGORH FGOR, MSCF/STB trong mô hình mô phỏng sẽ có bảng PVT 
 0,25
 FWCT.FWCTH dimensionless FWCT.FWCTH riêng, không bị hạn chế bởi cách chia số vùng 
 2
 hữu hạn. So sánh với cách áp dụng phương 
 0 0 0,00 pháp mô hình hóa PVT trước đó (theo cách 
 1/1/2016 1/1/2017 1/1/2018 thông thường, Hình 6), có thể thấy đặc tính 
 Thời gian
 PVT của chất lưu, chẳng hạn như áp suất bão 
 Hình 7. Kết quả phục hồi lịch sử khai thác mô hình tầng H mỏ BRS.
 hòa, được mô phỏng biến đổi liên tục theo 
lưu. Chẳng hạn như ở khí condensate, áp suất ngưng tụ bị ảnh hưởng không gian thay vì việc đồng nhất và trung 
mạnh bởi hàm lượng mol của C7+. Trong dầu nặng, thành phần C7+ bình hóa cho cả mô hình. Giải pháp này vừa 
ảnh hưởng lớn đến độ nhớt, thành tạo asphaltene và wax. Tương tự tiết giảm được số lượng mẫu cần thu thập và 
như vậy, trong dầu nhẹ, thể tích dầu và các tính chất khác ở áp suất phân tích, vừa chi tiết hóa được đặc tính PVT 
thấp hơn áp suất bão hòa được xác định bởi hàm lượng các thành phần của mỏ. Kết quả cũng giúp được việc phục 
trung bình và nặng. hồi số liệu lịch sử cho tham số GOR cũng như 
 Dựa trên số liệu ban đầu, mặc dù đã có đến 9 mẫu chất lưu, nhưng đảm bảo cân bằng vật chất của mô hình khai 
 thác đạt kết quả tốt hơn so với phương pháp 
các tham số PVT (thành phần cấu tử C1 và C7+, GOR, áp suất bão hòa...) 
có mối liên hệ kém do chất lượng mẫu và đo chưa đảm bảo, nhiều tạp trước đây (Hình 7). 
chất gây bẩn mẫu và ảnh hưởng đến kết quả đo. Trên cơ sở lý thuyết 4. Kết luận
về cân bằng nhiệt động học và phân ly trọng lực, kết hợp với phân 
tích đánh giá các số liệu thí nghiệm phân tích mẫu PVT từ các giếng Việc ứng dụng phương trình trạng thái 
khai thác trong vùng nghiên cứu, nhóm tác giả đã loại bỏ được các trong điều kiện cân bằng nhiệt động học 
yếu tố ảnh hưởng, đồng thời tìm ra quy luật về phân bố của những đặc giúp tiết giảm số lượng mẫu cần thu thập và 
tính PVT quan trọng nhất cũng như phương trình trạng thái EOS để mô phân tích, chi tiết và chính xác hóa được đặc 
phỏng động thái pha [1]. Kết quả cho thấy các tính chất quan trọng như tính PVT của các khu vực quanh các giếng 
hàm lượng thành phần các cấu tử, áp suất bão hòa, tỷ số khí hòa tan... khai thác hiện nay của mỏ, đồng thời là cơ 
có quan hệ với độ sâu vỉa (Hình 1 - 3). Kết quả mô phỏng phương trình sở đế tối ưu việc lấy mẫu và lựa chọn các chỉ 
EOS với số liệu phân tích thí nghiệm cho các thông số chính được trình tiêu phân tích cho các giếng ở giai đoạn tiếp 
bày ở Hình 4. theo. Mỗi một ô lưới khác nhau sẽ có bảng 
 PVT riêng (không bị hạn chế bởi cách chia số 
18 DẦUKHÍSỐ4/2021
 
vùng hữu hạn). Phương pháp này giúp kết quả phục hồi [2] Curtis H. Whitson and Michael R. Brule, Phase 
số liệu lịch sử khai thác của mô hình tốt hơn, từ đó tăng behavior. SPE Monograph Series, 2000.
tính tin cậy của mô hình dự báo. 
 [3] Hanafy Hussein and Ismail Shaban Mahgoub, 
Tài liệu tham khảo “Methodology of investgatin the commpositional 
 gradient within the hydrocarbon column”, SPE Annual 
 [1] Tarek Ahmed, Equation of state and PVT analysis: Technical Conference and Exhibition, Dallas, Texas, October 
Application for improved reservoir modeling. Gulf Publishing 2005. DOI: 10.2118/95760-MS.
Company, 2007.
USINGEQUATIONOFSTATE(EOS)TOENHANCECHARACTERISATION
OFPETROLEUMRESERVOIRFLUIDSWITHCOMPLEXBEHAVIOURS
Nguyen Hoang Duc, Tran Quoc Viet, Nguyen Hai An, Phung Van Hai
Petrovietnam Exploration Production corporation
Email: annh1@pvep.com.vn 
Summary
 For oil fields with complex fluid dynamics, to accurately simulate the oil and gas properties under pressure-volume-temperature 
(PVT) conditions it is often necessary to compartmentalise into sub-regions, collect and analyse many more fluid samples (in fact, in 
each hydrodynamic zone there must be at least one well to be sampled). However, the results are still not entirely correct. In addition, the 
level of detail is limited by a finite number of sub-regions while spatially, the fluid PVT properties of the reservoir change continuously.
 The paper presents the application of EOS in thermodynamic equilibrium in order to provide an effective method for modelling the 
fluid properties for each specific location in space (continuous variation) from Hamra reservoir in Touggourt, Sahara desert. Thus, it is 
possible to simulate the continuously variable fluid properties, minimise the need to carry out the collection and analysis of additional 
fluid samples and reduce costs. 
Key words: PVT, thermodynamic equilibrium, Equation of State, reservoir fluid simulation.
 DẦUKHÍSỐ4/2021 19