Ứng dụng giải thuật di truyền cho tối ưu lịch trình mạng cảm biến không dây theo thời gian

ng vấn đề sinh sản và duy trì nòi giống. 
Những cá thể có năng lực cao sẽ có khả năng sống sót 
cao và có số lượng con cái lớn hơn, các cá thể yếu 
hơn sẽ có ít con cái thậm chí không có con. Các thế 
hệ sau sẽ được thừa hưởng, kết hợp và phát triển 
những đặc điểm tốt từ bố mẹ nên con cái sẽ có năng 
lực cao hơn bố mẹ rất nhiều. Đây chính là cách mà 
các loài tiến hóa để thích nghi với môi trường sống. 
Thuật toán di truyền bắt chước tự nhiên với các 
nguyên lý tiến hóa như di truyền, chọn lọc tự nhiên, 
lai ghép và đột biến để tìm ra giải pháp tối ưu tổng 
thể cho một vấn đề, đặc biệt trong các bài toán liên 
quan đến vấn đề tìm kiếm hoặc tối ưu hóa. GA hoạt 
động với một tập hợp các cá thể, mỗi cá thể đại diện 
một giải pháp khả thi cho vấn đề nhất định và có một 
giá trị tùy thuộc vào mức độ giải quyết vấn đề đó. 
JST: Engineering and Technology for Sustainable Development 
Vol. 1, Issue 2, April 2021, 029-034 
31 
Những cá thể có tính phù hợp cao sẽ được lựa chọn 
và lai với nhau để tạo ra thế mới có năng lực tốt hơn 
bố mẹ. GA thường được ứng dụng cho những bài tối 
ưu như: lập kế hoạch [10], vận tải [11], tìm đường 
[12], chương trình trò chơi, điều khiển thích nghi,... 
Do những ưu điểm vượt trội, thuật toán di truyền 
ngày càng được phát triển và ứng dụng mạnh mẽ 
trong thực tế. GA đã được sử dụng trong tối ưu hóa 
cho mạng cảm biến, một bài toán rất phổ biến và 
quan trọng là tối ưu cơ chế lập lịch thực hiện các mục 
tiêu tối ưu hóa trong mạng cảm biến. 
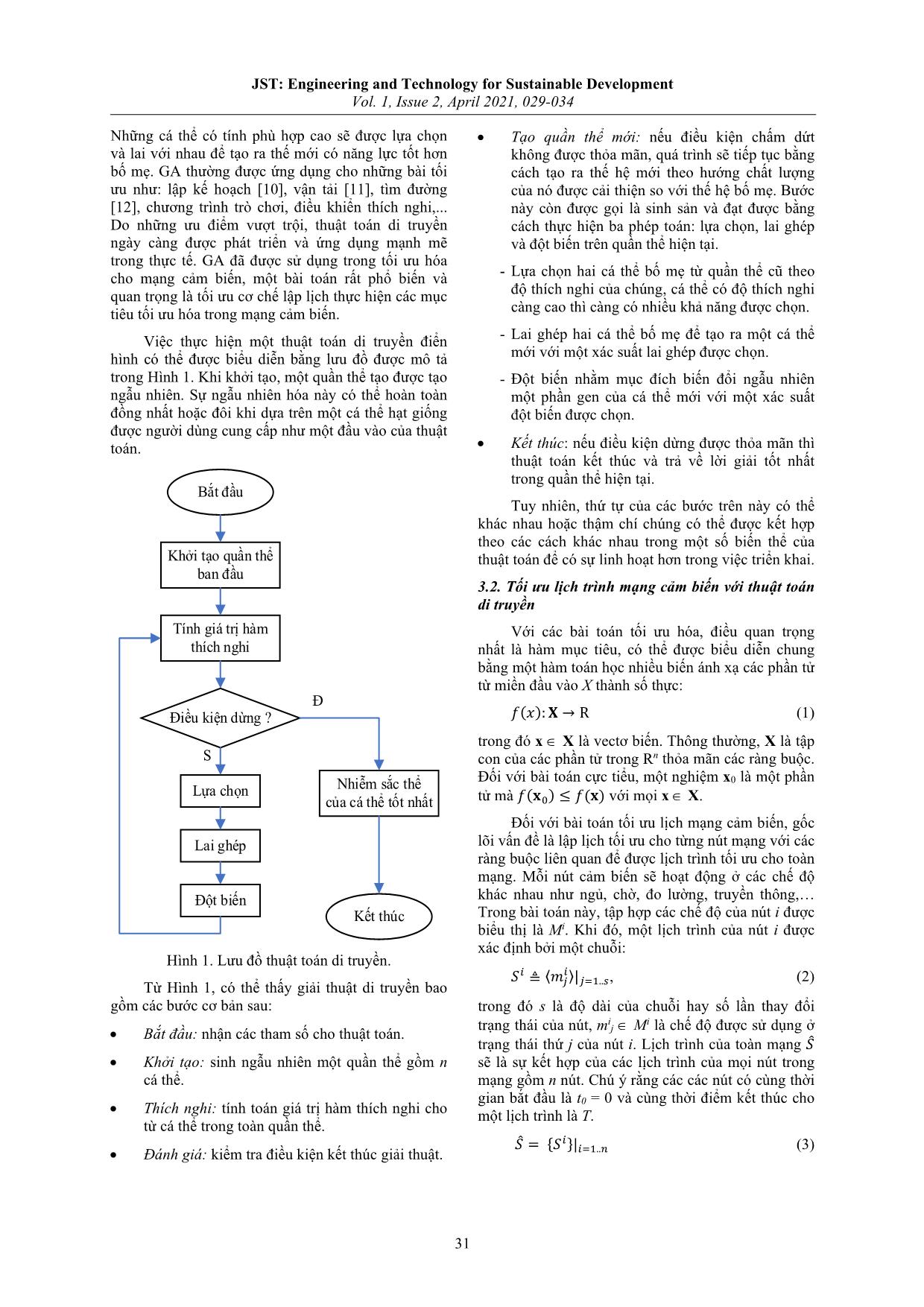
Việc thực hiện một thuật toán di truyền điển 
hình có thể được biểu diễn bằng lưu đồ được mô tả 
trong Hình 1. Khi khởi tạo, một quần thể tạo được tạo 
ngẫu nhiên. Sự ngẫu nhiên hóa này có thể hoàn toàn 
đồng nhất hoặc đôi khi dựa trên một cá thể hạt giống 
được người dùng cung cấp như một đầu vào của thuật 
toán. 
Hình 1. Lưu đồ thuật toán di truyền. 
Từ Hình 1, có thể thấy giải thuật di truyền bao 
gồm các bước cơ bản sau: 
• Bắt đầu: nhận các tham số cho thuật toán. 
• Khởi tạo: sinh ngẫu nhiên một quần thể gồm n 
cá thể. 
• Thích nghi: tính toán giá trị hàm thích nghi cho 
từ cá thể trong toàn quần thể. 
• Đánh giá: kiểm tra điều kiện kết thúc giải thuật. 
• Tạo quần thể mới: nếu điều kiện chấm dứt 
không được thỏa mãn, quá trình sẽ tiếp tục bằng 
cách tạo ra thế hệ mới theo hướng chất lượng 
của nó được cải thiện so với thế hệ bố mẹ. Bước 
này còn được gọi là sinh sản và đạt được bằng 
cách thực hiện ba phép toán: lựa chọn, lai ghép 
và đột biến trên quần thể hiện tại. 
- Lựa chọn hai cá thể bố mẹ từ quần thể cũ theo 
độ thích nghi của chúng, cá thể có độ thích nghi 
càng cao thì càng có nhiều khả năng được chọn. 
- Lai ghép hai cá thể bố mẹ để tạo ra một cá thể 
mới với một xác suất lai ghép được chọn. 
- Đột biến nhằm mục đích biến đổi ngẫu nhiên 
một phần gen của cá thể mới với một xác suất 
đột biến được chọn. 
• Kết thúc: nếu điều kiện dừng được thỏa mãn thì 
thuật toán kết thúc và trả về lời giải tốt nhất 
trong quần thể hiện tại. 
Tuy nhiên, thứ tự của các bước trên này có thể 
khác nhau hoặc thậm chí chúng có thể được kết hợp 
theo các cách khác nhau trong một số biến thể của 
thuật toán để có sự linh hoạt hơn trong việc triển khai. 
3.2. Tối ưu lịch trình mạng cảm biến với thuật toán 
di truyền 
Với các bài toán tối ưu hóa, điều quan trọng 
nhất là hàm mục tiêu, có thể được biểu diễn chung 
bằng một hàm toán học nhiều biến ánh xạ các phần tử 
từ miền đầu vào X thành số thực: 
𝑓𝑓(𝑥𝑥):𝐗𝐗 → R (1) 
trong đó x ∈ X là vectơ biến. Thông thường, X là tập 
con của các phần tử trong Rn thỏa mãn các ràng buộc. 
Đối với bài toán cực tiểu, một nghiệm x0 là một phần 
tử mà 𝑓𝑓(𝐱𝐱0) ≤ 𝑓𝑓(𝐱𝐱) với mọi x ∈ X. 
Đối với bài toán tối ưu lịch mạng cảm biến, gốc 
lõi vấn đề là lập lịch tối ưu cho từng nút mạng với các 
ràng buộc liên quan để được lịch trình tối ưu cho toàn 
mạng. Mỗi nút cảm biến sẽ hoạt động ở các chế độ 
khác nhau như ngủ, chờ, đo lường, truyền thông, 
Trong bài toán này, tập hợp các chế độ của nút i được 
biểu thị là Mi. Khi đó, một lịch trình của nút i được 
xác định bởi một chuỗi: 
𝑆𝑆𝑖𝑖 ≜ 〈𝑚𝑚𝑗𝑗
𝑖𝑖〉|𝑗𝑗=1..𝑠𝑠, (2) 
trong đó s là độ dài của chuỗi hay số lần thay đổi 
trạng thái của nút, mij ∈ Mi là chế độ được sử dụng ở 
trạng thái thứ j của nút i. Lịch trình của toàn mạng �̂�𝑆 
sẽ là sự kết hợp của các lịch trình của mọi nút trong 
mạng gồm n nút. Chú ý rằng các các nút có cùng thời 
gian bắt đầu là t0 = 0 và cùng thời điểm kết thúc cho 
một lịch trình là T. 
 �̂�𝑆 = {𝑆𝑆𝑖𝑖}|𝑖𝑖=1..𝑛𝑛 (3) 
Bắt đầu
Khởi tạo quần thể 
ban đầu
Tính giá trị hàm 
thích nghi
Nhiễm sắc thể 
của cá thể tốt nhất
Điều kiện dừng ?
Lựa chọn
Lai ghép
Đột biến
Kết thúc
S
Đ
JST: Engineering and Technology for Sustainable Development 
Vol. 1, Issue 2, April 2021, 029-034 
32 
Trong nghiên cứu này, nhiễm sắc thể mã hóa 
lịch trình mạng �̂�𝑆 được định nghĩa như sau: 
 1 1 11 2[ , , , ,sC m m m=  
 2 2 21 2 , , , , sm m m 
1 2 , , , 
n n n
sm m m ]. (4) 
Số gen của mỗi nút là s và của toàn mạng là 
(n×s). Giả sử quần thể có p cá thể, khi đó qC|q=1..p 
biểu thị lịch trình của cá thể q trong quần thể lịch 
trình mạng, và qCi, như thể hiện trên Hình 2, là biểu 
thị đoạn gen trong qC tương ứng lịch trình của nút i 
trong lịch trình mạng q. Tương tự, tất cả các biến phụ 
thuộc cá thể khác cũng tuân theo quy ước ký hiệu 
này, ví dụ, q𝑚𝑚𝑗𝑗
𝑖𝑖 là trạng thái j của nút i của cá thể q. 
Lịch trình của nút i được biểu diễn như sau: 
qCi = [q 1
im , q 2 ,
im , q ism ]. (5) 
Theo đó, lịch trình của mạng gồm n nút qC sẽ 
được biểu diễn như sau: 
qC = [qC1, qC2,, qCn ]. (6) 
Hình 2. Biểu diễn lịch trình hoạt động của một nút. 
4. Kịch bản và kết quả mô phỏng 
Trong khuôn khổ bài báo này, một kịch bản thử 
nghiệm thuật toán di truyền cho lớp bài toán tối ưu 
lịch trình mạng với mục tiêu cụ thể là tối đa hóa số 
giá trị đo thông số môi trường, với ràng buộc là tuổi 
thọ của nút và đảm bảo thời gian giữa hai lần đo liên 
tiếp không lớn hơn Δτ cho trước. Đối với mỗi nút 
cảm biến, cần phải biết trước các thông số về năng 
lượng tiêu thụ của nút như dung lượng lớn nhất của 
pin, tốc độ sạc pin, năng lượng tiêu thụ của từng chế 
độ làm việc. Thực tế, các nút cảm biến có thể có 
nhiều chế độ làm việc như ngủ, chờ, đo lường và 
truyền thông, Tuy nhiên, trong bài toán này ràng 
buộc là tối đa tuổi thọ mạng nên vấn đề năng lượng 
tiêu thụ được đặc biệt quan tâm. Vì vậy trong kịch 
bản này, để đơn giản, mỗi nút sẽ được xem xét với 2 
chế độ là chế độ là ngủ M- tiêu thụ năng lượng ở mức 
thấp và chế độ hoạt động M+ tiêu thụ năng lượng ở 
mức cao. Như vậy Mi = {M-, M+}. Giả sử thời gian 
toàn lịch trình được chia thành các khoảng bằng nhau 
và mỗi khoảng là τ, khi đó τ×s = T. 
Kịch bản thử nghiệm với mạng gồm 3 nút cảm 
biến. Để đơn giản, giả sử rằng các nút có cấu hình 
tương tự nhau và chỉ có sự khác biệt về dung lượng 
tối đa của pin. Nhóm đã phát triển và thực nghiệm 3 
nút cảm biến đo nhiệt độ và độ ẩm không khí trong 
quá trình nghiên cứu [13], và các tham số cơ bản của 
các nút trong mạng thực nghiệm được đưa ra như 
trong Bảng 1. Các mô phỏng được thực hiện bằng 
nền tảng mô phỏng đã được nhóm nghiên cứu phát 
triển và giới thiệu cụ thể hơn trong [14]. 
Bảng 1. Tham số các nút mạng của kịch bản 
Tham số Nút 1 Nút 2 Nút 3 
Dung lượng pin tối đa (mAh) 3500 5250 7000 
Tốc độ sạc pin (W) 0.8 0.8 0.8 
Mức tiêu thụ ở chế độ ngủ (W) 0.05 0.05 0.05 
Mức tiêu thụ năng lượng trung 
bình ở chế độ chờ (W) 0.17 0.17 0.17 
Mức tiêu thụ năng lượng trung 
bình ở chế độ đo lường (W) 0.22 0.22 0.22 
Mức tiêu thụ trung bình ở một lần 
truyền thông (W) 13.27 13.27 13.27 
Δτ (phút) 5 5 5 
T (ngày) 3 3 3 
Ngoài ra, trong kịch bản mô phỏng, vị trí, tọa độ 
của nút trong không gian cũng cần được quan tâm và 
xác định cụ thể vì nó liên quan đến vấn đề thu năng 
lượng. Để tối đa hoá số lần đo thực hiện được của 
mạng, đồng thời đảm bảo các yếu tố về năng lượng 
và thời gian hoạt động, hàm mục tiêu được sử dụng là 
một hàm gồm 4 thành phần: 
1 2 3 4 ,Φ = Φ +Φ +Φ +Φ (7) 
trong đó, 1Φ là thành phần tương ứng với số lần đo 
cần tối đa hoá, 2Φ là thành phần giúp hạn chế các 
khoảng thời gian dài mà không có phép đo nào được 
thực hiện, 3Φ để hạn chế việc các nút bị hết pin trước 
khi kết thúc kịch bản chạy, và 4Φ để hạn chế việc mức 
pin cuối chu kỳ mô phỏng nhỏ hơn khi bắt đầu. Cụ thể, 
1 ,kηηΦ = − (8) 
2
2 1 2
1
,i i
i
k k
η
τ ττ τ
=
Φ = ∆ + ∆∑ (9) 
( ) ( )23 1 2 ,T Tk T T k T TΦ = − + −  (10) 
( ) ( )21 2
4
 if ,
0 if ,
L e s L e s e s
e s
k L L k L L L L
L L
 − + − <Φ = 
≥
 (11) 
trong đó η là số lần đo thực hiện được; iτ∆ là thời 
gian giữa hai lần đo liên tiếp; T là thời điểm nút bị hết 
pin, hoặc bằng T nếu không hết; sL và eL là các mức 
pin khi bắt đầu và kết thúc chu kỳ; và kη , 1kτ , 2kτ , 
1Tk , 2Tk , 1Lk , 2Lk là các hệ số với giá trị hằng. Các 
hàm bậc hai sử dụng cho 2 4−Φ nhằm giúp thuật toán 
q iC
7
q it2
q it 3
q it 4
q it 5
q it 6
q it t1
q it 8
q it
JST: Engineering and Technology for Sustainable Development 
Vol. 1, Issue 2, April 2021, 029-034 
33 
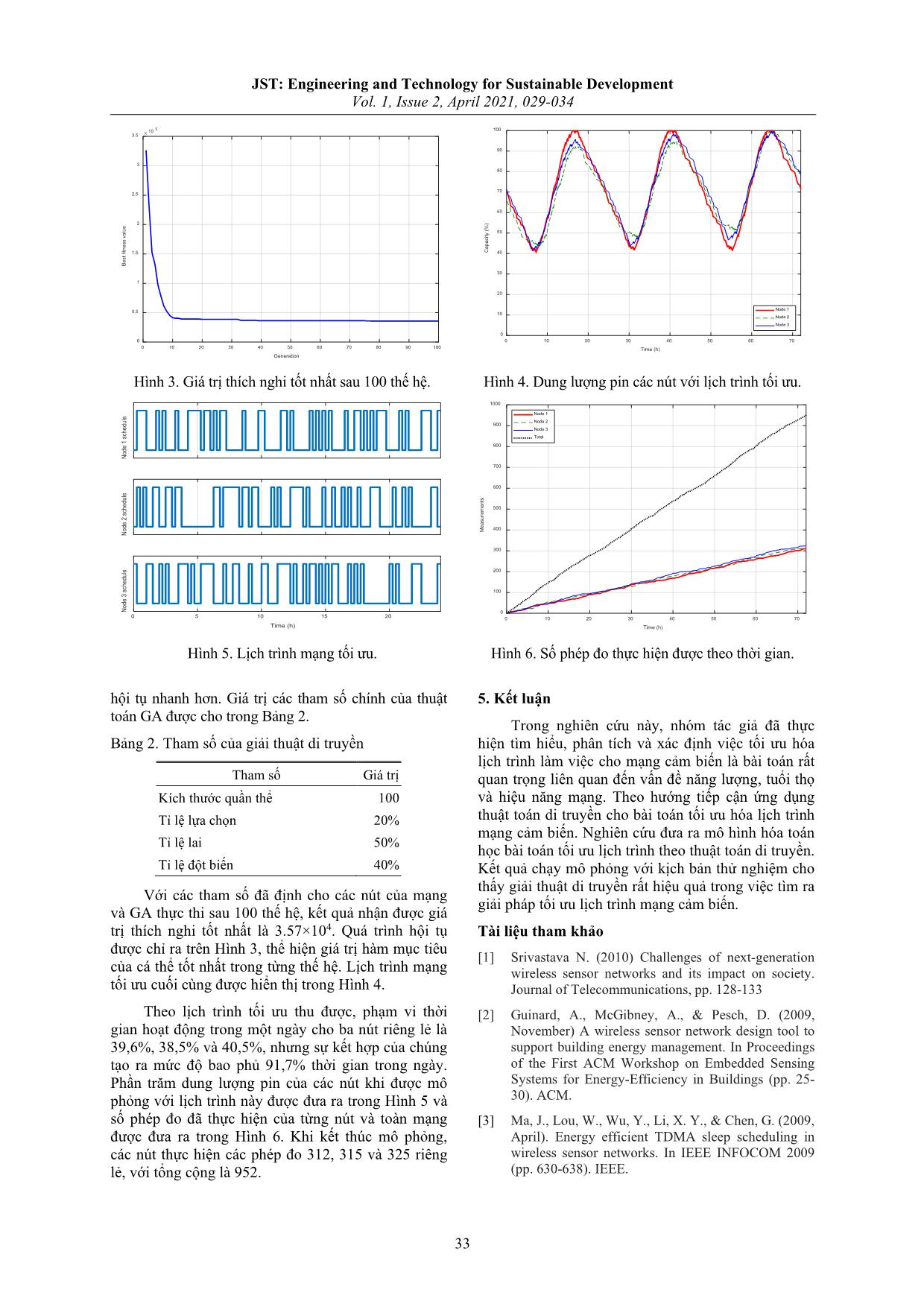
Hình 3. Giá trị thích nghi tốt nhất sau 100 thế hệ. Hình 4. Dung lượng pin các nút với lịch trình tối ưu. 
Hình 5. Lịch trình mạng tối ưu. Hình 6. Số phép đo thực hiện được theo thời gian. 
hội tụ nhanh hơn. Giá trị các tham số chính của thuật 
toán GA được cho trong Bảng 2. 
Bảng 2. Tham số của giải thuật di truyền 
Tham số Giá trị 
Kích thước quần thể 100 
Tỉ lệ lựa chọn 20% 
Tỉ lệ lai 50% 
Tỉ lệ đột biến 40% 
Với các tham số đã định cho các nút của mạng 
và GA thực thi sau 100 thế hệ, kết quả nhận được giá 
trị thích nghi tốt nhất là 3.57×104. Quá trình hội tụ 
được chỉ ra trên Hình 3, thể hiện giá trị hàm mục tiêu 
của cá thể tốt nhất trong từng thế hệ. Lịch trình mạng 
tối ưu cuối cùng được hiển thị trong Hình 4. 
Theo lịch trình tối ưu thu được, phạm vi thời 
gian hoạt động trong một ngày cho ba nút riêng lẻ là 
39,6%, 38,5% và 40,5%, nhưng sự kết hợp của chúng 
tạo ra mức độ bao phủ 91,7% thời gian trong ngày. 
Phần trăm dung lượng pin của các nút khi được mô 
phỏng với lịch trình này được đưa ra trong Hình 5 và 
số phép đo đã thực hiện của từng nút và toàn mạng 
được đưa ra trong Hình 6. Khi kết thúc mô phỏng, 
các nút thực hiện các phép đo 312, 315 và 325 riêng 
lẻ, với tổng cộng là 952. 
5. Kết luận 
Trong nghiên cứu này, nhóm tác giả đã thực 
hiện tìm hiểu, phân tích và xác định việc tối ưu hóa 
lịch trình làm việc cho mạng cảm biến là bài toán rất 
quan trọng liên quan đến vấn đề năng lượng, tuổi thọ 
và hiệu năng mạng. Theo hướng tiếp cận ứng dụng 
thuật toán di truyền cho bài toán tối ưu hóa lịch trình 
mạng cảm biến. Nghiên cứu đưa ra mô hình hóa toán 
học bài toán tối ưu lịch trình theo thuật toán di truyền. 
Kết quả chạy mô phỏng với kịch bản thử nghiệm cho 
thấy giải thuật di truyền rất hiệu quả trong việc tìm ra 
giải pháp tối ưu lịch trình mạng cảm biến. 
Tài liệu tham khảo 
[1] Srivastava N. (2010) Challenges of next-generation 
wireless sensor networks and its impact on society. 
Journal of Telecommunications, pp. 128-133 
[2] Guinard, A., McGibney, A., & Pesch, D. (2009, 
November) A wireless sensor network design tool to 
support building energy management. In Proceedings 
of the First ACM Workshop on Embedded Sensing 
Systems for Energy-Efficiency in Buildings (pp. 25-
30). ACM. 
[3] Ma, J., Lou, W., Wu, Y., Li, X. Y., & Chen, G. (2009, 
April). Energy efficient TDMA sleep scheduling in 
wireless sensor networks. In IEEE INFOCOM 2009 
(pp. 630-638). IEEE. 
0 10 20 30 40 50 60 70 80 90 100
Generation
0
0.5
1
1.5
2
2.5
3
3.5
B
es
t f
itn
es
s 
va
lu
e
10 5
0 10 20 30 40 50 60 70
Time (h)
0
10
20
30
40
50
60
70
80
90
100
C
ap
ac
ity
 (%
)
Node 1
Node 2
Node 3
N
od
e 
1 
sc
he
du
le
N
od
e 
2 
sc
he
du
le
0 5 10 15 20
Time (h)
N
od
e 
3 
sc
he
du
le
0 10 20 30 40 50 60 70
Time (h)
0
100
200
300
400
500
600
700
800
900
1000
M
ea
su
re
m
en
ts
Node 1
Node 2
Node 3
Total
JST: Engineering and Technology for Sustainable Development 
Vol. 1, Issue 2, April 2021, 029-034 
34 
[4] L. Wang, and X. Yang. “A survey of energy-efficient 
scheduling mechanisms in sensor networks,” Mobile 
Networks and Applications, vol. 11, no. 5, pp. 723-
740, 2006. 
[5] Berman, P., Calinescu, G., Shah, C., & Zelikovsly, A. 
(2005). Efficient energy management in sensor 
networks. In Y. Xiao & Y. Pan (Eds.), Ad hoc and 
sensor networks. Nova Science. 
[6] Tian, D., & Georganas, N. D. (2002). A coverage-
preserving node scheduling scheme for large wireless 
sensor networks. In Proceedings of the 1st ACM 
International Workshop on Wireless Sensor Networks 
and Applications (WSNA ’02) (pp. 32–41), Atlanta, 
Georgia. 
[7] Heinzelman, W. R., Chandrakasan, A., & 
Balakrishnan, H. (2000, January). Energy-efficient 
communication protocol for wireless microsensor 
networks. In Proceedings of the 33rd annual Hawaii 
international conference on system sciences (pp. 10-
pp). IEEE. 
[8] He, T., Krishnamurthy, S., Stankovic, J. A., 
Abdelzaher, T., Luo, L., Stoleru, R. et al. (2004). 
Energy-efficient surveillance system using wireless 
sensor networks. In Proceedings of the 2nd 
International Conference on Mobile Systems, 
Applications, and Services (MobiSys ’04) (pp. 270–
283), Boston, Massachusetts. 
[9] J. H. Holland, Adaptation in Natural and Artificial 
Systems, The University of Michigan Press, 
Michigan, 1975. 
[10] Lee, S. C., Tseng, H. E., Chang, C. C., & Huang, Y. 
M. (2019). Applying Interactive Genetic Algorithms 
to Disassembly Sequence Planning. International 
Journal of Precision Engineering and Manufacturing, 
1-17. 
[11] Liu, T. K., Lin, S. S., & Hsueh, P. W. (2019). 
Optimal design for transport and logistics of steel mill 
by-product based on double-layer genetic algorithms. 
Journal of Low Frequency Noise, Vibration and 
Active Control, 1461348419872368. 
[12] Al-Furhud, M. A., & Ahmed, Z. H. (2020). Genetic 
Algorithms for the Multiple Travelling Salesman 
Problem. International Journal of Advanced 
Computer Science and Applications (IJACSA), 11(7), 
553-560. 
[13] Nguyễn, T. H., Lê, M. H., Đào, T. K., Hà, V. P., & 
Phạm, T. N. Y. (2020). Thiết kế, chế tạo nút cảm biến 
có khả năng tùy biến phục vụ nghiên cứu, phát triển 
nền tảng mô phỏng mạng cảm biến. Tạp chí Khoa học 
và công nghệ, 56(4), 26-30. 
[14] Ha, V.P., Dao, T.K., Le, M.H., Nguyen, T.H., and 
Nguyen, V.T. 2020. Design and implementation of 
an energy simulation platform for wireless sensor 
networks. 2020 IEEE International Conference on 
Multimedia Analysis and Pattern Recognition 
(MAPR). Hanoi, Vietnam, Oct. 
JST: Engineering and Technology for Sustainable Development 
Vol. 1, Issue 2, April 2021, 029-034 
35