Mô hình hóa mặt cong tham số bậc thấp từ lưới tam giác dựa trên phương pháp dịch chuyển hình học cục bộ

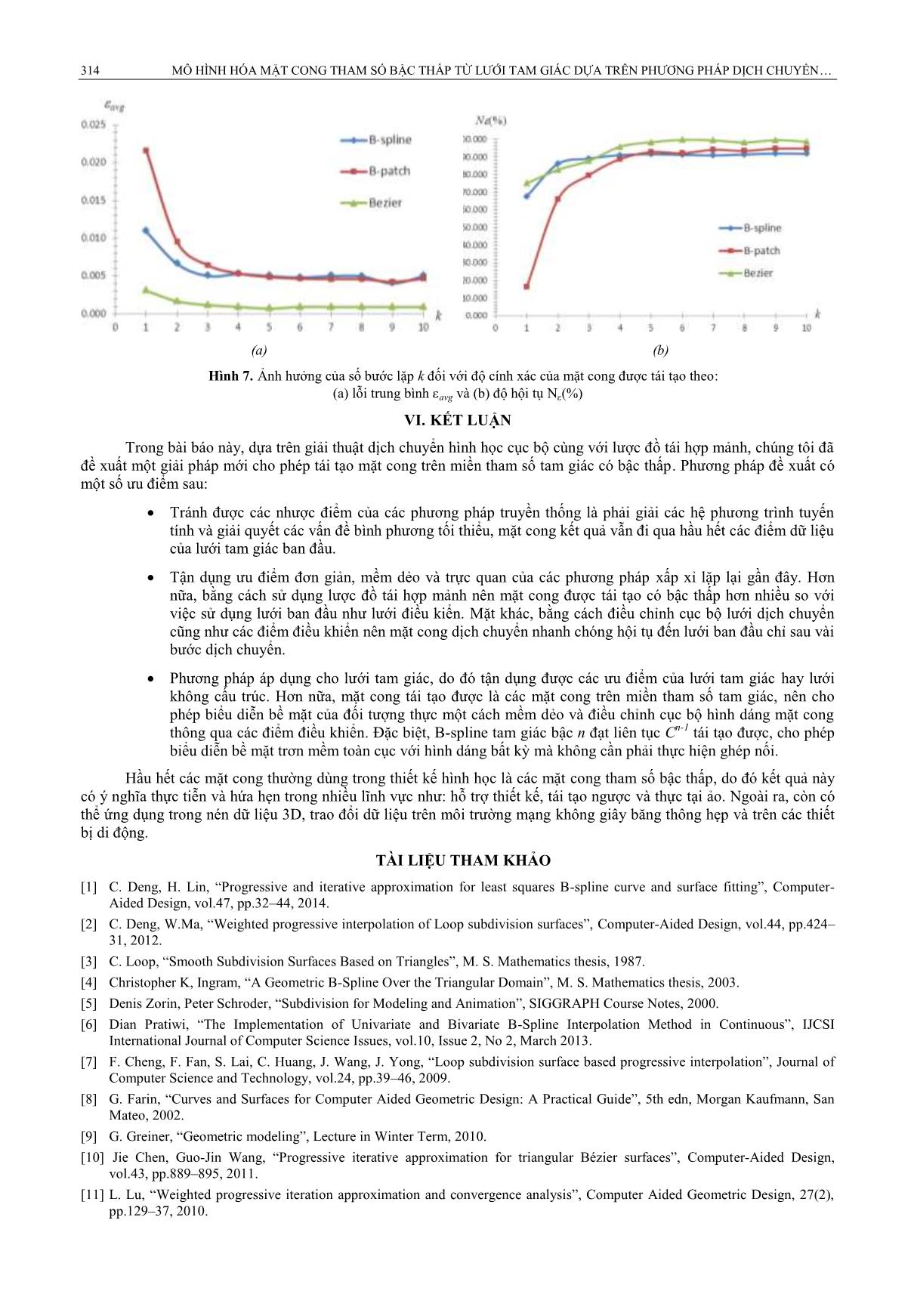
 điều khiển của mặt cong. 
 Cập nhật lại đám mây nút trong miền tham số của mặt cong. 
 i i
 4. Ứng với mỗi điểm dữ liệu pj, xác định các véctơ lỗi j . Trong đó j là độ lệch giữa các điểm dữ liệu so 
 với mặt cong dịch chuyển Si. 
 i
 5. Dựa trên các véctơ lỗi j , điều chỉnh lại lƣới dịch chuyển cũng nhƣ các điểm điều khiển của mặt cong. 
 Nhờ đó mà mặt cong dịch chuyển cũng đƣợc điều chỉnh lại cho dần hội tụ đến các điểm dữ liệu của lƣới 
 ban đầu. 
 Trong quá trình dịch chuyển, một chuỗi các lƣới dịch chuyển đƣợc tạo ra, cập nhật và đƣợc thô hóa. Từ đó, một 
chuỗi các mặt cong tƣơng ứng cũng lần lƣợt đƣợc sinh ra và dội tụ dần về phía lƣới ban đầu. Qua mỗi bƣớc dịch 
 i
chuyển, véctơ lỗi trung bình avg giảm dần. Quá trình dịch chuyển dừng khi véctơ lỗi trung bình bé hơn dung sai Sau 
một số bƣớc dịch chuyển hình học cục bộ, mặt cong tham số tái tạo đƣợc nội suy hầu hết các điểm dữ liệu của lƣới ban 
đầu với lỗi trung bình nhỏ nhất. Giải thuật đƣợc thể hiện chi tiết thông qua sơ đồ trong Hình 3. 
 Start M0 = triMesh(p | ) 
 j j=1..m
 M* = M0 ; k = 0 
 Mi = invSub(M*, i) k ++ 
 i i * *
 S = paraSurf(M ) M = triMesh(p j | j=1..m) 
 i i * i
 j = errVect(pj,S ) p j = pj+j 
 No 
  i = errAvg( i) i
 avg j avg <= 
 Yes 
 S = paraSurf(Mi) End 
 Hình 3. Sơ đồ giải thuật dịch chuyển hình học cục bộ 
312 MÔ HÌNH HÓA MẶT CONG THAM SỐ BẬC THẤP TỪ LƢỚI TAM GIÁC DỰA TRÊN PHƢƠNG PHÁP DỊCH CHUYỂN 
 Các ký hiệu trong sơ đồ có ý nghĩa nhƣ sau: 
 0 0 
 M = triMesh(pj| j=1..m): Dựng lƣới tam giác M từ m các điểm dữ liệu pj. 
 i * i * 
 M = invSub(M , i): Tạo lƣới thô M từ lƣới dịch chuyển M thông qua i lần tái hợp mảnh. 
 i i i i
 S = paraSurf(M ): Sinh mặt cong tham số tam giác S bằng cách sử dụng lƣới M làm lƣới điều khiển. 
 i i i
 j = errVect(pj,S ): Xác định các véctơ lỗi j ứng với mỗi điểm dữ liệu pj. 
 i i i
 avg = errAvg(j ): Tính véctơ lỗi trung bình dựa trên các véctơ lỗi j . 
 Giả sử rằng quá trình dịch chuyển mặt cong thực hiện k lần, khi đó, giá trị k phụ thuộc vào dung sai . Với m 
điểm dữ liệu pj, giải thuật dịch chuyển hình học cục bộ để tái tạo mặt cong tham số tam giác S sẽ có độ phức tạp 
 mk () 
 V. KẾT QUẢ THỰC NGHIỆM 
 Để có đƣợc các kết quả thực nghiệm, chúng tôi đã cài đặt giải thuật đề xuất trên máy tính cá nhân Pentium dual 
core CPU 2.16GHz với 1.0GB RAM, sử dụng Microsoft VC++ và thƣ viện đồ họa mở OpenGL. Ứng với các mô hình 
thực nghiệm dùng để tái tạo các mặt cong trên miền tham số tam giác nhƣ Bézier tam giác, B-patch và B-spline tam 
giác, chúng tôi đều xem xét bậc, độ chính xác, độ cong của mặt cong đạt đƣợc và thời gian thực hiện của thuật toán. 
 Gọi i là số lần tái hợp mảnh Loop; k là số bƣớc lặp khi thực hiện giải thuật dịch chuyển hình học cục bộ; avg là 
độ lệch trung bình tính đƣợc tại lần tái hợp mảnh i và bƣớc dịch chuyển k; N là độ hội tụ của mặt cong ứng với dung 
sai và N đƣợc tính bằng tỉ lệ phần trăm của số điểm dữ liệu đi qua mặt cong đạt đƣợc so với tổng các điểm dữ liệu 
của lƣới tam giác ban đầu. Khi đó, các mô hình lƣới thực nghiệm, một số kết quả tính toán và các mặt cong tham số tái 
tạo tƣơng ứng đƣợc liệt kê trong Bảng 1. 
 Bảng 1. Các mô hình thực nghiệm và mặt cong kết quả đạt đƣợc tƣơng ứng 
 Lưới khởi tạo Kết quả tính toán Mặt cong tham số được tái tạo 
 Mô hình Số Số Thời Số điểm Số tam giác 
 i k  N (%) Mặt cong Bậc 
 điểm mặt avg  gian(s) điều khiển miền tham số 
 BézierMesh 561 1024 1 6 0.0009291 99.756 <1 Bézier 16 153 1 
 BpatchMesh 153 256 2 10 0.004664 94.771 22 B-patch 4 15 1 
 BsplineMesh 3681 7168 3 9 0.004034 91.979 114 B-spline 2 69 28 
 Mô hình đầu tiên để tái tạo mặt cong tham số Bézier tam giác là lƣới tam giác BézierMesh bao gồm 561 điểm và 
1024 mặt (Hình 4a). Nếu dùng lƣới này nhƣ lƣới điều khiển của mặt cong dịch chuyển thì mặt cong thu đƣợc sẽ có bậc 
n=32. Tuy nhiên, để giảm bậc của mặt cong kết quả, chúng tôi đã áp dụng lƣợc đồ tái hợp mảnh Loop lên lƣới này và 
sử dụng lƣới kết quả nhƣ lƣới điều khiển của mặt cong dịch chuyển, sau k = 2, 4, 6 bƣớc dịch chuyển hình học cục bộ, 
Bézier kết quả nhanh chóng hội tụ về lƣới ban đầu (Hình 4b,c,d). Hình 4d và 4e cho thấy mặt cong đạt đƣợc đi qua hầu 
hết các điểm dữ liệu, đó là một Bézier tam giác có bậc n = 16 và nhận 153 điểm làm điểm điều khiển. Hình 4f hiển thị 
Bézier tái tạo đƣợc cùng với độ cong Gaussian của mặt cong. Thời gian tái tạo Bézier này khá nhanh, chƣa tới 1 giây 
cho k = 6 bƣớc dịch chuyển hình học, với độ lệch trung bình khá nhỏ, avg = 0.0009291, và độ hội tụ cao, N = 99.756%. 
 (a) (b) (c) 
 (d) (e) (f) 
 Hình 4. Tái tạo mặt cong Bézier tam giác: (a) Lƣới khởi tạo, (b,c,d) mặt cong đạt đƣợc sau k=2,4,6 bƣớc dịch chuyển, 
 (e) mặt trong của mặt cong (d), và (f) độ cong Gaussian của Bézier kết quả với bậc n=16 
Lê Thị Thu Nga, Nguyễn Tấn Khôi, Nguyễn Thanh Thủy 313 
 Mô hình thứ hai BpatchMesh đƣợc hiển thị trong Hình 5a, thông tin về lƣới tam giác này nhƣ trong Bảng 1. Sau 
khi áp dụng i=2 lần tái hợp mảnh Loop, chúng tôi thu đƣợc lƣới thô chỉ còn 15 điểm điều khiển và 16 mặt. Dùng lƣới 
thô kết quả để dựng mặt cong tham số B-patch và dịch chuyển hình học mặt cong này bằng cách điều chỉnh cục bộ lƣới 
dịch chuyển theo các véctơ lỗi. Sau k=10 bƣớc dịch chuyển, B-patch thu đƣợc là một mặt cong tham số bậc n=4 (Hình 
5b). Mặt cong này đạt đƣợc tại độ lệch trung bình avg = 0.004664 và độ hội tụ khá cao, N = 94.771%. 
 (a) (b) (c) (d) 
 Hình 5. Tái tạo mặt cong B-patch: (a) Lƣới khởi tạo, (b) B-patch bậc n=4 đạt đƣợc sau k=10 bƣớc dịch chuyển, 
 (c) mapping zebra của (b), và (f) miền tham số cùng với các đám mây nút của B-patch kết quả 
 Hình 6a minh họa mô hình thứ ba, lƣới tam giác BsplineMesh, gồm 3681 điểm và 7168 mặt. Để có đƣợc lƣới 
điều khiển của mặt cong dịch chuyển B-spline với bậc thấp, chúng tôi áp dụng i=3 lần tái hợp mảnh Loop lên lƣới này. 
Kết quả thu đƣợc là một lƣới tam giác điều khiển chỉ còn 69 điểm. Từ lƣới thô kết quả, chúng tôi dựng mặt cong B-
spline bậc n=2, với miền tham số là một lƣới phẳng gồm 28 tam giác (Hình 6f). Sau k=3, 6, 9 bƣớc dịch chuyển hình 
học cục bộ (Hình 6b, c, d), mặt cong B-spline trên miền tham số tam giác có bậc n=2 đạt đƣợc với độ lệch trung bình 
khá nhỏ, avg = 0.004034, và độ hội tụ khá cao N = 91.979%. Mặc dù cần phải xác định rất nhiều Spline đơn hình để 
tính tọa độ của một điểm trên mặt cong, nhƣng thời gian để tái tạo B-spline này không quá hai phút. 
 (a) (b) (c) 
 (d) (e) (f) 
 Hình 6. Tái tạo mặt cong B-spline tam giác: (a) Lƣới khởi tạo, (b,c,d) mặt cong đạt đƣợc sau k=3,6,9 bƣớc dịch chuyển, 
 (e) lƣới điều khiển và B-spline kết quả bậc n=2, và (f) miền tham số cùng với các đám mây nút của B-spline kết quả 
 Cuối cùng, để đánh giá độ chính xác của các mặt cong Bézier tam giác, B-patch và B-spline tam giác đƣợc tái 
tạo so với các mô hình lƣới tam giác ban đầu, cũng nhƣ tốc độ hội tụ của giải thuật dịch chuyển hình học cục bộ trong 
các bƣớc lặp k, Hình 7 minh họa sự ảnh hƣởng này thông qua độ lệch trung bình avg và độ hội tụ N. Hình 7a cho thấy 
độ lệch trung bình avg của cả ba mô hình phụ thuộc mạnh mẽ vào số bƣớc dịch chuyển k, đặc biệt chúng giảm mạnh 
trong bốn bƣớc đầu tiên. Các độ lệch này tƣơng đối ổn đinh từ bƣớc thứ năm trở đi và nằm trong khoảng từ 0.004 đến 
0.005 (đối với B-patch, B-spline tam giác) và từ 0.0007 đến 0.0009 (đối với Bézier tam giác). Điều này cho thấy các 
mặt cong tham số đạt đƣợc nhanh chóng hội tụ về các điểm dữ liệu chỉ sau vài bƣớc dịch chuyển hình học. Tƣơng tự, 
các đồ thị trong Hình 7b cho thấy số bƣớc lặp càng tăng thì độ hội tụ N theo bƣớc dịch chuyển k càng cao. Các giá trị 
N này cũng tăng nhanh trong bốn bƣớc đầu và sau đó dần chạm ngƣỡng 92% (đối với B-spline tam giác), 95% (đối 
với B-patch) và 100% (đối với Bézier tam giác). Sở dĩ việc tái tạo mặt cong Bézier tam giác cho kết quả cao hơn so với 
hai dạng mặt cong còn lại có thể giải thích đƣợc là do miền tham số của mặt cong Bézier chỉ đơn thuần là một tam giác 
miền. Trong khi đó B-patch và B-spline, bên cạnh miền tham số tam giác còn có các đám mây nút. Cấu hình các đám 
mây nút này cũng ảnh hƣởng đến hình dáng của mặt cong. 
314 MÔ HÌNH HÓA MẶT CONG THAM SỐ BẬC THẤP TỪ LƢỚI TAM GIÁC DỰA TRÊN PHƢƠNG PHÁP DỊCH CHUYỂN 
 (a) (b) 
 Hình 7. Ảnh hƣởng của số bƣớc lặp k đối với độ cính xác của mặt cong đƣợc tái tạo theo: 
 (a) lỗi trung bình avg và (b) độ hội tụ N(%) 
 VI. KẾT LUẬN 
 Trong bài báo này, dựa trên giải thuật dịch chuyển hình học cục bộ cùng với lƣợc đồ tái hợp mảnh, chúng tôi đã 
đề xuất một giải pháp mới cho phép tái tạo mặt cong trên miền tham số tam giác có bậc thấp. Phƣơng pháp đề xuất có 
một số ƣu điểm sau: 
 Tránh đƣợc các nhƣợc điểm của các phƣơng pháp truyền thống là phải giải các hệ phƣơng trình tuyến 
 tính và giải quyết các vấn đề bình phƣơng tối thiểu, mặt cong kết quả vẫn đi qua hầu hết các điểm dữ liệu 
 của lƣới tam giác ban đầu. 
 Tận dụng ƣu điểm đơn giản, mềm dẻo và trực quan của các phƣơng pháp xấp xỉ lặp lại gần đây. Hơn 
 nữa, bằng cách sử dụng lƣợc đồ tái hợp mảnh nên mặt cong đƣợc tái tạo có bậc thấp hơn nhiều so với 
 việc sử dụng lƣới ban đầu nhƣ lƣới điều kiển. Mặt khác, bằng cách điều chỉnh cục bộ lƣới dịch chuyển 
 cũng nhƣ các điểm điều khiển nên mặt cong dịch chuyển nhanh chóng hội tụ đến lƣới ban đầu chỉ sau vài 
 bƣớc dịch chuyển. 
 Phƣơng pháp áp dụng cho lƣới tam giác, do đó tận dụng đƣợc các ƣu điểm của lƣới tam giác hay lƣới 
 không cấu trúc. Hơn nữa, mặt cong tái tạo đƣợc là các mặt cong trên miền tham số tam giác, nên cho 
 phép biểu diễn bề mặt của đối tƣợng thực một cách mềm dẻo và điều chỉnh cục bộ hình dáng mặt cong 
 thông qua các điểm điều khiển. Đặc biệt, B-spline tam giác bậc n đạt liên tục Cn-1 tái tạo đƣợc, cho phép 
 biểu diễn bề mặt trơn mềm toàn cục với hình dáng bất kỳ mà không cần phải thực hiện ghép nối. 
 Hầu hết các mặt cong thƣờng dùng trong thiết kế hình học là các mặt cong tham số bậc thấp, do đó kết quả này 
có ý nghĩa thực tiễn và hứa hẹn trong nhiều lĩnh vực nhƣ: hỗ trợ thiết kế, tái tạo ngƣợc và thực tại ảo. Ngoài ra, còn có 
thể ứng dụng trong nén dữ liệu 3D, trao đổi dữ liệu trên môi trƣờng mạng không giây băng thông hẹp và trên các thiết 
bị di động. 
 TÀI LIỆU THAM KHẢO 
[1] C. Deng, H. Lin, “Progressive and iterative approximation for least squares B-spline curve and surface fitting”, Computer-
 Aided Design, vol.47, pp.32–44, 2014. 
[2] C. Deng, W.Ma, “Weighted progressive interpolation of Loop subdivision surfaces”, Computer-Aided Design, vol.44, pp.424–
 31, 2012. 
[3] C. Loop, “Smooth Subdivision Surfaces Based on Triangles”, M. S. Mathematics thesis, 1987. 
[4] Christopher K, Ingram, “A Geometric B-Spline Over the Triangular Domain”, M. S. Mathematics thesis, 2003. 
[5] Denis Zorin, Peter Schroder, “Subdivision for Modeling and Animation”, SIGGRAPH Course Notes, 2000. 
[6] Dian Pratiwi, “The Implementation of Univariate and Bivariate B-Spline Interpolation Method in Continuous”, IJCSI 
 International Journal of Computer Science Issues, vol.10, Issue 2, No 2, March 2013. 
[7] F. Cheng, F. Fan, S. Lai, C. Huang, J. Wang, J. Yong, “Loop subdivision surface based progressive interpolation”, Journal of 
 Computer Science and Technology, vol.24, pp.39–46, 2009. 
[8] G. Farin, “Curves and Surfaces for Computer Aided Geometric Design: A Practical Guide”, 5th edn, Morgan Kaufmann, San 
 Mateo, 2002. 
[9] G. Greiner, “Geometric modeling”, Lecture in Winter Term, 2010. 
[10] Jie Chen, Guo-Jin Wang, “Progressive iterative approximation for triangular Bézier surfaces”, Computer-Aided Design, 
 vol.43, pp.889–895, 2011. 
[11] L. Lu, “Weighted progressive iteration approximation and convergence analysis”, Computer Aided Geometric Design, 27(2), 
 pp.129–37, 2010. 
Lê Thị Thu Nga, Nguyễn Tấn Khôi, Nguyễn Thanh Thủy 315 
[12] M. Eck, H. Hoppe, “Automatic reconstruction of B-spline surfaces of arbitrary topological type”, In Proceedings of 
 SIGGRAPH96, ACM Press, pp.325–334, 1996. 
[13] M. Botsch, M. Pauly, C. Rossl, S. Bischoff and L. Kobbelt, “Geometric Modeling Based on Triangle Meshes”, EuroGraphics, 
 2006. 
[14] M. Halstead, M. Kass, T. Derose, “Efficient, fair interpolation using Catmull-Clark surfaces”, In Proceedings of ACM 
 SIGGRAPH 93, pp. 35–44, 1993. 
[15] Neamtu M, “Bivariate simplex B-splines: a new paradigm”, In Proceedings of the 17th spring conference on computer 
 graphics, pp.71–78, 2001. 
[16] Seidel HP, “Symmetric recursive algorithms for surfaces: b-patches and the de Boor algorithm for polynomials over triangles”, 
 Constructive Approximation, 7, 257–279, 1991. 
[17] T. Maekawa, Y. Matsumoto, K. Namiki, “Interpolation by geometric algorithm”, Computer-Aided Design, vol.39, pp.313–323, 
 2007. 
[18] W. Dahmen, C. A. Micchelli, and H. P. Seidel, “Blossoming begets B-spline bases built better by B-patches”, Mathematics of 
 Computation, 59(199), pp 97-115, 1992. 
[19] Y. Kineri, M. Wang, H. Lin, T. Maekawa, “B-spline surface fitting by iterative geometric interpolation/ approximation 
 algorithms”, Computer-Aided Design, vol.44(7), pp.697–708, 2012. 
[20] Y. Nishiyama, M. Morioka, T. Maekawa, “Loop subdivision surface fitting by geometric algorithms”, Poster proceedings of 
 pacific graphics, 2008. 
[21] Y. Xiong, G. Li, A. Mao, “Convergence analysis for B-spline geometric interpolation”, Computers & Graphics, vol.36, 
 pp.884–891, 2012. 
[22] Yu Zhao, Hongwei Lin, “The PIA property of low degree non-uniform triangular B-B patches”, In Proceedings of the 12th 
 International Conference on CAD and CG, pp.239-243, 2011. 
 MODELING LOW DEGREE PARAMETRIC SURFACES 
 FROM TRIANGULAR MESHES 
 BASED ON LOCAL GEOMETRIC FITTING METHOD 
 Nga Le Thi Thu, Khoi Nguyen Tan, Thuy Nguyen Thanh 
ABSTRACT— Reconstruction of parametric surface from triangular mesh, especially for the surfaces with low degree, has 
practical significance and is promising in areas such as reverse engineering, virtual reality and CAGD. This paper introduces a 
novel approach to reconstruct low degree parametric surfaces over the triangular domain, particularly triangular Bezier, B-patch, 
triangular B-spline, based on inverse subdivision scheme and local geometric fitting method. By using a simplified initial triangular 
mesh as a control polyhedron of the parametric surface and adjusting the control points iteratively, the obtained surface crosses 
through most data points of the given mesh without solving any linear system. All control points of the fitting surface, as well as 
knotclouds of its parametric domain, are iteratively adjusted locally to increase the accuracy of the reconstructed surface. The 
experimental results show that proposed method is simple, flexible and can be successfully applied to triangular meshes with 
arbitrary topology. 
Keywords — Parametric surface, triangular mesh, geometric fitting, inverse subdivision, surface reconstruction.