Thuật toán tìm kiếm Hill climbing giải bài toán Cây Steiner nhỏ nhất

ều kiện đa dạng hóa){ ngôn ngữ C++ sử dụng môi trường DEV C++ 5.9.2;
 28 Loại bỏ một số cạnh ngẫu nhiên của được thực nghiệm trên một máy chủ ảo, Hệ điều hành
 Cây Steiner đang xét; Windows server 2008 R2 Enterprise 64bit, Intel(R)
 29 Chọn ngẫu nhiên một số cạnh trong
 các cạnh còn lại của đồ thị cho Xeon (R) CPU E5-2660 @ 2.20 GHz, RAM 4GB.
 đến khi cây liên thông trở lại (điều
 kiện cạnh thêm vào là: Phải có đỉnh
 C. Kết quả thực nghiệm và đánh giá
 thuộc mới được thêm vào để tránh
 trường hợp thêm vào quá nhiều lần Kết quả thực nghiệm của các thuật toán được ghi
 nhưng không liên thông trở lại). Sử nhận ở các Bảng I,II,III. Các bảng này có cấu trúc
 dụng định nghĩa k-lân cận ở trên;
 như sau: Cột đầu tiên (Test) là tên các bộ dữ liệu
 30 Nếu thêm quá nhiều lần mà không
 làm cho liên thông trở lại, thì tiếp trong hệ thống dữ liệu thực nghiệm, số đỉnh (푛),
 tục đa dạng hóa lại với các cạnh số cạnh ( ) của từng đồ thị, các cột tiếp theo ghi
 khác; nhận giá trị chi phí Cây Steiner lần lượt ứng với hai
31 } thuật toán hueristic: Heu [26], PD [21]. Hai thuật
32 } toán metahueristic: VNS [23], TS [5] và thuật toán
33 }
 HCSMT.
34 return 푒푠푡 ;
 Bộ tham số được xác định như sau qua thực nghiệm:
 Số lần chạy mỗi bộ dữ liệu là 30, số lần tăng cường
 là 50; số cạnh loại bỏ ngẫu nhiên của mỗi lần tăng
 Steiner lân cận. Tính đa dạng được sử dụng vào các cường là 0.05×| ( )|.
 5
 Tập 2020, Số 1, Tháng 6
 Bảng I Bảng II
 KẾT QUẢ THỰC NGHIỆM THUẬT KẾT QUẢ THỰC NGHIỆM THUẬT
 TOÁN TRÊN NHÓM ĐỒ THỊ STEINC TOÁN TRÊN NHÓM ĐỒ THỊ STEIND
 HC HC
 Test n m Heu PD VNS TS Test n m Heu PD VNS TS
 SMT SMT
 steinc1.txt 500 625 85 85 85 85 85 steind1.txt 1000 1250 106 107 106 106 106
 steinc2.txt 500 625 144 144 144 144 144 steind2.txt 1000 1250 220 228 220 220 220
 steinc3.txt 500 625 755 762 754 754 754 steind3.txt 1000 1250 1570 1771 1565 1567 1565
 steinc4.txt 500 625 1080 1085 1079 1079 1080 steind4.txt 1000 1250 1936 2174 1935 1935 1936
 steinc5.txt 500 625 1579 1583 1579 1579 1579 steind5.txt 1000 1250 3252 3511 3250 3250 3250
 steinc6.txt 500 1000 55 55 55 55 55 steind6.txt 1000 2000 70 70 67 70 67
 steinc7.txt 500 1000 102 102 102 102 102 steind7.txt 1000 2000 103 111 103 103 103
 steinc8.txt 500 1000 510 516 509 509 509 steind8.txt 1000 2000 1092 1287 1073 1078 1073
 steinc9.txt 500 1000 715 718 707 707 707 steind9.txt 1000 2000 1462 1773 1448 1450 1448
 steinc10.txt 500 1000 1093 1107 1093 1093 1093 steind10.txt 1000 2000 2113 2550 2111 2112 2113
 steinc11.txt 500 2500 32 34 33 32 32 steind11.txt 1000 5000 29 29 29 30 29
 steinc12.txt 500 2500 46 48 46 46 46 steind12.txt 1000 5000 42 44 42 42 42
 steinc13.txt 500 2500 262 268 258 258 258 steind13.txt 1000 5000 510 643 502 502 507
 steinc14.txt 500 2500 324 332 323 324 324 steind14.txt 1000 5000 675 851 671 667 674
 steinc15.txt 500 2500 557 562 556 556 557 steind15.txt 1000 5000 1120 1437 1116 1117 1118
 steinc16.txt 500 12500 11 12 11 11 11 steind16.txt 1000 25000 13 13 13 13 13
 steinc17.txt 500 12500 19 20 18 18 18 steind17.txt 1000 25000 23 25 23 23 23
 steinc18.txt 500 12500 120 123 115 117 115 steind18.txt 1000 25000 238 301 228 230 231
 steinc19.txt 500 12500 150 159 148 148 149 steind19.txt 1000 25000 325 424 318 315 321
 steinc20.txt 500 12500 268 268 268 267 268 steind20.txt 1000 25000 539 691 538 538 539
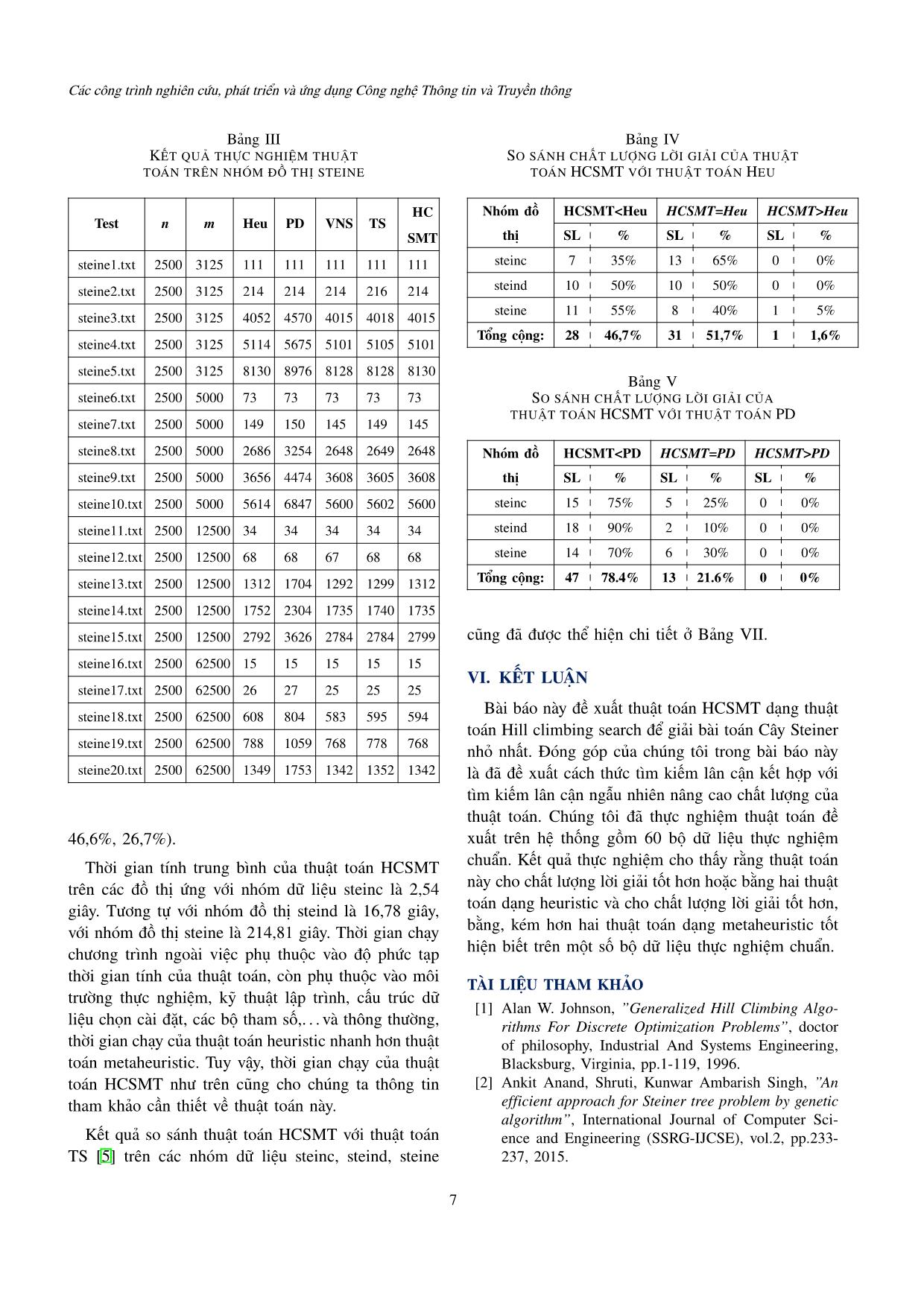
D. Đánh giá kết quả thực nghiệm tiết ở Bảng IV.
 Mục này nhằm so sánh chất lượng lời giải của thuật Tương tự, kết quả so sánh thuật toán HCSMT với
toán HCSMT với hai thuật toán heuristic: Heu [26], thuật toán PD [21] trên các nhóm dữ liệu steinc,
PD [21] và hai thuật toán metaheuristic: VNS [23], steind, steine cũng đã được thể hiện chi tiết ở Bảng
TS [5]. Nội dung của Bảng IV,V,VI,VII cho biết số V.
lượng (SL) và tỉ lệ phần trăm (%) tương ứng với số Kết quả so sánh thuật toán HCSMT với thuật toán
lượng bộ dữ liệu cho chất lượng lời giải tốt hơn (ghi VNS [23] trên các nhóm dữ liệu steinc, steind, steine
nhận bởi ký hiệu "<") hoặc cho chất lượng lời giải cũng đã được thể hiện chi tiết ở Bảng VI.
bằng nhau (ghi nhận bởi ký hiệu "=") hoặc cho chất Đánh giá chung trên toàn bộ 60 bộ dữ liệu, thuật
lượng lời giải kém hơn (ghi nhận bởi ký hiệu ">") khi toán HCSMT cho chất lượng lời giải (tốt hơn, bằng,
so sánh thuật toán HCSMT với các thuật toán: Heu kém hơn) thuật toán Heu [26] (46,7%, 51,7%, 1,6%).
[26], PD [21], VNS [23] và TS [5]. Thuật toán HCSMT cho chất lượng lời giải (tốt hơn,
 Với 20 bộ dữ liệu nhóm steinc, thuật toán HCSMT bằng, kém hơn) thuật toán PD [21] (78,4%, 21,6%,
cho chất lượng lời giải (tốt hơn, bằng, kém hơn) thuật 0,0%). Thuật toán HCSMT cho chất lượng lời giải (tốt
toán Heu [26] (35,0%, 65,0%, 0,0%). Kết quả so sánh hơn, bằng, kém hơn) thuật toán VNS [23] (1,7%, 70%,
thuật toán HCSMT với thuật toán Heu [26] trên các 28,3%). Thuật toán HCSMT cho chất lượng lời giải
nhóm dữ liệu steind, steine cũng đã được thể hiện chi (tốt hơn, bằng, kém hơn) thuật toán TS [5] (26,7%,
 6
Các công trình nghiên cứu, phát triển và ứng dụng Công nghệ Thông tin và Truyền thông
 Bảng III Bảng IV
 KẾT QUẢ THỰC NGHIỆM THUẬT SO SÁNH CHẤT LƯỢNG LỜI GIẢI CỦA THUẬT
 TOÁN TRÊN NHÓM ĐỒ THỊ STEINE TOÁN HCSMT VỚI THUẬT TOÁN HEU
 HC Nhóm đồ HCSMTHeu
 Test n m Heu PD VNS TS
 SMT thị SL % SL % SL %
 steine1.txt 2500 3125 111 111 111 111 111 steinc 7 35% 13 65% 0 0%
 steine2.txt 2500 3125 214 214 214 216 214 steind 10 50% 10 50% 0 0%
 steine 11 55% 8 40% 1 5%
 steine3.txt 2500 3125 4052 4570 4015 4018 4015
 Tổng cộng: 28 46,7% 31 51,7% 1 1,6%
 steine4.txt 2500 3125 5114 5675 5101 5105 5101
 steine5.txt 2500 3125 8130 8976 8128 8128 8130
 Bảng V
 steine6.txt 2500 5000 73 73 73 73 73 SO SÁNH CHẤT LƯỢNG LỜI GIẢI CỦA
 THUẬT TOÁN HCSMT VỚI THUẬT TOÁN PD
 steine7.txt 2500 5000 149 150 145 149 145
 steine8.txt 2500 5000 2686 3254 2648 2649 2648 Nhóm đồ HCSMTPD
 steine9.txt 2500 5000 3656 4474 3608 3605 3608 thị SL % SL % SL %
 steine10.txt 2500 5000 5614 6847 5600 5602 5600 steinc 15 75% 5 25% 0 0%
 steine11.txt 2500 12500 34 34 34 34 34 steind 18 90% 2 10% 0 0%
 steine12.txt 2500 12500 68 68 67 68 68 steine 14 70% 6 30% 0 0%
 steine13.txt 2500 12500 1312 1704 1292 1299 1312 Tổng cộng: 47 78.4% 13 21.6% 0 0%
 steine14.txt 2500 12500 1752 2304 1735 1740 1735
 steine15.txt 2500 12500 2792 3626 2784 2784 2799 cũng đã được thể hiện chi tiết ở Bảng VII.
 steine16.txt 2500 62500 15 15 15 15 15
 VI. KẾT LUẬN
 steine17.txt 2500 62500 26 27 25 25 25
 Bài báo này đề xuất thuật toán HCSMT dạng thuật
 steine18.txt 2500 62500 608 804 583 595 594
 toán Hill climbing search để giải bài toán Cây Steiner
 steine19.txt 2500 62500 788 1059 768 778 768 nhỏ nhất. Đóng góp của chúng tôi trong bài báo này
 steine20.txt 2500 62500 1349 1753 1342 1352 1342 là đã đề xuất cách thức tìm kiếm lân cận kết hợp với
 tìm kiếm lân cận ngẫu nhiên nâng cao chất lượng của
 thuật toán. Chúng tôi đã thực nghiệm thuật toán đề
46,6%, 26,7%). xuất trên hệ thống gồm 60 bộ dữ liệu thực nghiệm
 Thời gian tính trung bình của thuật toán HCSMT chuẩn. Kết quả thực nghiệm cho thấy rằng thuật toán
trên các đồ thị ứng với nhóm dữ liệu steinc là 2,54 này cho chất lượng lời giải tốt hơn hoặc bằng hai thuật
giây. Tương tự với nhóm đồ thị steind là 16,78 giây, toán dạng heuristic và cho chất lượng lời giải tốt hơn,
với nhóm đồ thị steine là 214,81 giây. Thời gian chạy bằng, kém hơn hai thuật toán dạng metaheuristic tốt
chương trình ngoài việc phụ thuộc vào độ phức tạp hiện biết trên một số bộ dữ liệu thực nghiệm chuẩn.
thời gian tính của thuật toán, còn phụ thuộc vào môi
 TÀI LIỆU THAM KHẢO
trường thực nghiệm, kỹ thuật lập trình, cấu trúc dữ
 [1] Alan W. Johnson, ”Generalized Hill Climbing Algo-
liệu chọn cài đặt, các bộ tham số,. . . và thông thường, rithms For Discrete Optimization Problems”, doctor
thời gian chạy của thuật toán heuristic nhanh hơn thuật of philosophy, Industrial And Systems Engineering,
toán metaheuristic. Tuy vậy, thời gian chạy của thuật Blacksburg, Virginia, pp.1-119, 1996.
toán HCSMT như trên cũng cho chúng ta thông tin [2] Ankit Anand, Shruti, Kunwar Ambarish Singh, ”An
tham khảo cần thiết về thuật toán này. efficient approach for Steiner tree problem by genetic
 algorithm”, International Journal of Computer Sci-
 Kết quả so sánh thuật toán HCSMT với thuật toán ence and Engineering (SSRG-IJCSE), vol.2, pp.233-
TS [5] trên các nhóm dữ liệu steinc, steind, steine 237, 2015.
 7
 Tập 2020, Số 1, Tháng 6
 Bảng VI on Steiner tree problems”, pp.1-36, 2015.
 SO SÁNH CHẤT LƯỢNG LỜI GIẢI CỦA THUẬT [13] Marcello Caleffi, Ian F. Akyildiz, Luigi Paura, ”On
 TOÁN HCSMT VỚI THUẬT TOÁN VNS the solution of the Steiner tree np-hard problem via
 physarum bionetwork”, IEEE, pp.1092-1106, 2015.
 Nhóm đồ HCSMTVNS [14] Nguyen Viet Huy, Nguyen Duc Nghia, ”Solving
 thị SL % SL % SL % graphical Steiner tree problem using parallel genetic
 algorithm”, RIVF, 2008.
 steinc 1 5% 15 75% 4 20%
 [15] Ondra Suchy, ”Exact algorithms for Steiner tree”,
 steind 0 0% 12 60% 8 40% Faculty of Information Technology, Czech Technical
 steine 0 0% 15 75% 5 25% University in Prague, Prague, Czech Republic, 2014.
 [16] Phan Tấn Quốc, ”Rút gọn đồ thị cho bài toán Cây
 Tổng
 1 1.7% 42 70% 17 28.3% Steiner nhỏ nhất”, Kỷ yếu Hội nghị Quốc gia lần thứ
 cộng: IX về Nghiên cứu cơ bản và ứng dụng Công nghệ
 thông tin (FAIR), Viện Công nghệ thông tin, Viện
 Hàn lâm Khoa học và Công nghệ Việt Nam, Trường
 Bảng VII Đại học Cần Thơ, ngày 04-05/08/2016, ISBN: 978-
 SO SÁNH CHẤT LƯỢNG LỜI GIẢI CỦA 604-913-472-2, trang 638-644, 2016.
 THUẬT TOÁN HCSMT VỚI THUẬT TOÁN TS
 [17] Poompat Saengudomlert, ”Optimization for Commu-
 nications and Networks”, Taylor and Francis Group,
 Nhóm đồ HCSMTTS LLC, pp.1-201, 2011.
 thị SL % SL % SL % [18] Reyan Ahmed and et al, ”Multi-level Steiner tree”,
 steinc 1 5% 15 75% 4 20% ACM J. Exp. Algor., 1(1), 2018.
 [19] S.L. Martins, M.G.C. Resende, C.C. Ribeiro, and P.M.
 steind 5 25% 7 35% 8 40% Pardalos, ”A parallel grasp for the Steiner tree prob-
 steine 10 50% 6 30% 4 20% lem in graphs using a hybrid local search strategy”,
 Tổng cộng: 16 26,7% 28 46,6% 16 26,7% 1999.
 [20] Stefan Hougardy, Jannik Silvanus, Jens Vygen, ”Dijk-
 stra meets Steiner: a fast-exact goal-oriented Steiner
 tree algorithm”, Research Institute for Discrete Math-
 [3] Arie M.C.A. Koster, Xavier Munoz (Eds), ”Graphs ematics, University of Bonn, pp.1-59, 2015.
 and algorithms in communication networks”, [21] Trần Việt Chương, Phan Tấn Quốc, Hà Hải Nam,
 Springer, pp.1-177, 2010. ”Đề xuất một số thuật toán heuristic giải bài toán
 [4] Bang Ye Wu, Kun-Mao Chao, ”Spanning trees and Cây Steiner nhỏ nhất”, Kỷ yếu Hội nghị Quốc gia
 optimization problems”, Chapman&Hall/CRC, pp.13- lần thứ X về Nghiên cứu cơ bản và ứng dụng Công
 139, 2004. nghệ thông tin (FAIR), Trường Đại học Đà Nẳng, ngày
 [5] C. C. RIBEIRO, M.C. SOUZA, ”Tabu Search for the 17-18/08/2017, ISBN: 978-604-913-614-6, trang 138-
 Steiner problem in graphs”, Networks, 36, pp.138- 147, 2017.
 146, 2000. [22] Trần Việt Chương, Phan Tấn Quốc, Hà Hải Nam,
 [6] Chi-Yeh Chen, ”An efficient approximation algorithm ”Thuật toán Bees giải bài toán Cây Steiner nhỏ nhất
 for the Steiner tree problem”, National Cheng Kung trong trường hợp đồ thị thưa”. Tạp chí khoa học công
 University, Taiwan, 2018. nghệ thông tin và truyền thông, Học viên Công nghệ
 [7] Eduardo Uchoa, Renato F. Werneck, ”Fast local Bưu chính Viễn thông, Bộ Thông tin và Truyền thông,
 search for Steiner trees in graphs”, SIAM, 2010. ISSN: 2525-2224, tháng 12, trang 24-29, 2017.
 [8] J. E. Beasley, OR-Library: URL [23] Tran Viet Chuong, Ha Hai Nam ”A variable neigh-
  mastjjb/jeb/orlib/stein- borhood search algorithm forsolving the Steiner min-
 info.html imal tree problem in sparse graphs”, Context-Aware
 [9] J. E. Beasley, ”An SST-Based algorithm for the Steiner Systems and Applications, and Nature of Computa-
 problem in graphs”, Networks, 19, pp.1-16, 1989. tion and Communication, EAI, Springer, pp.218-225,
[10] Jeffrey H. Kingston, Nicholas Paul Sheppard, ”On 2018.
 reductions for the Steiner problem in graphs”, Basser [24] Thomas Pajor, Eduardo Uchoa, Renato F. Werneck, ”A
 Department of Computer Science the University of robust and scalable algorithm for the Steiner problem
 Sydney, Australia, pp.1-10, 2006. in graphs”, Springer, 2018.
[11] Jon William Van Laarhoven, ”Exact and heuristic [25] Thomas Bosman, ”A solution merging heuristic for
 algorithms for the euclidean Steiner tree problem”, the Steiner problem in graphs using tree decomposi-
 University of Iowa, 2010 (Doctoral thesis). tions”, VU University Amsterdam, The Netherlands,
[12] M. Hauptmann, M. Karpinski (Eds), ”A compendium
 8
Các công trình nghiên cứu, phát triển và ứng dụng Công nghệ Thông tin và Truyền thông
 pp.1-12, 2015. SƠ LƯỢC VỀ CÁC TÁC GIẢ
[26] Thorsten Koch, Alexander Martin, ”Solving Steiner
 tree problems in graphs to optimality”, Germany, Trần Việt Chương
 pp.1-31, 1996.
[27] Trần Lê Thủy, ”Về bài toán Steiner”, Viện Toán học, Sinh ngày: 01/12/1974
 Viện Hàn lâm Khoa học và Công nghệ Việt Nam,
 2014 (luận văn thạc sĩ). Nhận bằng Thạc sỹ Khoa học
[28] Vũ Đình Hòa, ”Bài toán Steiner”,  máy tính năm 2005 tại Trường
[29] Wassim Jaziri (Edited). ”Local Search Techniques: Đại học Sư phạm I Hà Nội.
 Focus on Tabu Search”. In-teh, Vienna, Austria, pp.1- Hiện công tác tại Trung tâm
 201, 2008. CNTT và Truyền thông tỉnh Cà
[30] Xinhui Wang, ”Exact algorithms for the Steiner tree Mau, Sở Thông tin và Truyền
 problem”, doctoral thesis, ISSN 1381-3617, 2008.
 thông tỉnh Cà Mau. Lĩnh vực
[31] Xiuzhen Cheng, Ding-zhu Du, ”Steiner trees in indus-
 try”, Kluwer Academic Publishers, vol.5, pp.193-216, nghiên cứu: Thuật toán tiến hóa
 2004. và tối ưu.
[32] Xin-she Yang. ”Engineering optimization”. Wiley, Điện thoại: 0913 688 477
 pp.21-137, 2010. E-mail: chuongtv@camau.gov.vn
[33] S. E. Dreyfus, R. A. Wagner, ”The Steiner Problem
 in Graphs”, Networks, Vol.1, pp.195-207, 1971.
[34] L. Kou, G. Markowsky, L. Berman, ”A Fast Algorithm Phan Quốc Tấn
 for Steiner Trees”, acta informatica, Vol.15, pp.141-
 145, 1981. Sinh ngày: 12/10/1971
 Nhận bằng Thạc sỹ Tin học
 tại Trường Đại học KHTN -
 ĐHQG TP.HCM năm 2002, Tiến
 sỹ chuyên ngành Khoa học máy
 tính tại Trường Đại học Bách
 Khoa Hà Nội năm 2015.
 Hiện công tác tại Bộ môn Khoa
 học Máy tính, khoa Công nghệ
 Thông tin, Trường Đại học Sài
 Gòn. Lĩnh vực nghiên cứu: Thuật toán gần đúng.
 Điện thoại: 0918 178 052
 E-mail: quocpt@sgu.edu.vn
 Hà Hải Nam
 Sinh ngày: 10/02/1975
 Nhận bằng Thạc sỹ Tin học
 năm 2004 tại Trường Đại học
 Bách Khoa Hà Nội, Tiến sỹ năm
 2008 tại Vương quốc Anh. Được
 phong học hàm PGS năm 2014
 Hiện công tác tại Viện Khoa
 học Kỹ thuật Bưu điện, Học
 viện Công nghệ Bưu chính Viễn
 thông. Lĩnh vực nghiên cứu: Hệ
 thống phân tán và tối ưu hóa.
 Điện thoại: 091 66 34567
 E-mail: namhh@ptit.edu.vn
 9