Thuật toán hiệu quả khai thác tập phổ biến tối đại trên cơ sở dữ liệu giao dịch lớn

bản ghi phân biệt gọi là tập các giao dịch T = {T1, T2,..., Tn}, mỗi giao dịch Ti={Ik1, Ik2,..., Ikj}, Ikj I (1≤ kj ≤ m). 
 Cơ sở dữ liệu được nén như sau: 
 - Có m item tương ứng với m biến Bool; 
 m m m
 - CSDL có tối đa (2 – 1) giao dịch phân biệt tương ứng (2 – 1) đơn thức tối tiểu – mti (1≤ i < 2 ); 
 - Cấu trúc dữ liệu lưu trữ đơn thức tối tiểu, gồm: – mỗi bộ 
 lưu trữ được nhóm 8 đơn thức tối tiểu. 
 - Đơn thức tối tiểu mti được lưu vào bộ 
 Bảng 4. Các giao dịch trên CSDL biểu diễn dạng thập phân 
 Mã giao dịch A B C D E F G H Giá trị thập phân 
 T1 1 0 1 0 1 1 0 0 172 
 T2 1 0 1 0 0 0 1 0 162 
 T3 0 0 0 0 1 0 0 1 9 
 T4 1 0 1 1 0 1 1 0 182 
 T5 1 0 1 0 1 0 1 0 170 
 T6 0 0 0 0 1 0 0 0 8 
 T7 1 1 1 0 1 0 0 0 232 
 T8 1 0 1 1 0 0 0 0 176 
 T9 1 1 1 0 1 0 1 0 234 
 T10 1 0 1 0 1 1 1 0 174 
 Bảng 3, biểu diễn các giao dịch trên CSDL dưới dạng thập phân tương ứng với thứ tự của các đơn thức tối tiểu 
lần lượt là {mt8, mt9, mt162, mt170, mt172, mt174, mt176, mt182, mt232, mt234}. Áp dụng kỹ thuật nén dữ liệu tương ứng 10 đơn 
thức tối tiểu sẽ trở thành: 
724 THUẬT TOÁN HIỆU QUẢ KHAI THÁC TẬP PHỔ BIẾN TỐI ĐẠI TRÊN CƠ SỞ DỮ LIỆU GIAO DỊCH LỚN 
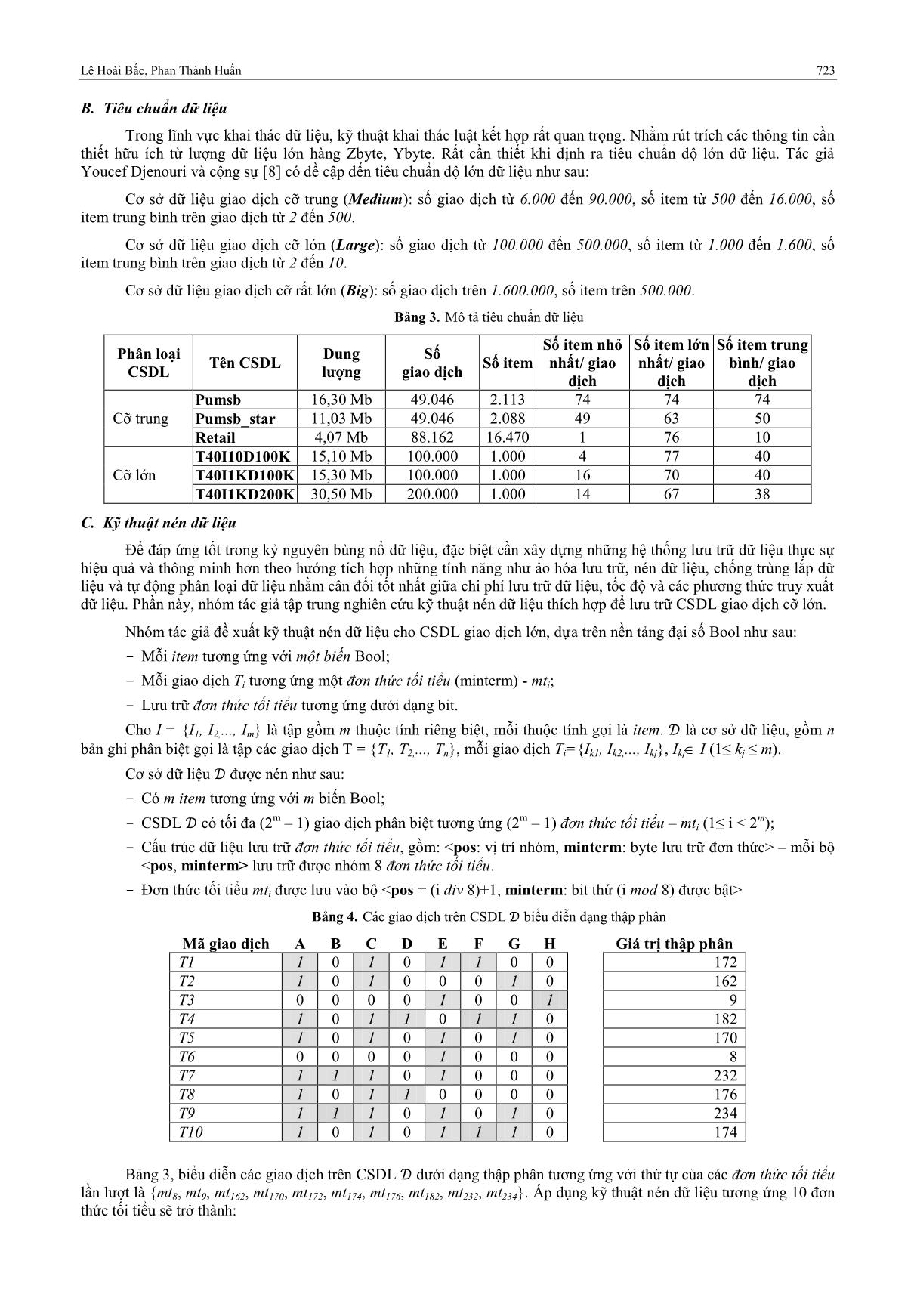
 pos 2 21 22 23 30 
 minterm 00000011 00000100 01010100 01000001 00000101 
 Hình 1. Nén CSDL 
 Hình 1, Kết quả nén CSDL gồm 10 giao dịch tương ứng thành 10 đơn thức tối tiểu {mt8, mt9, mt162, mt170, 
mt172, mt174, mt176, mt182, mt232, mt234} vào trong danh sách gồm 5 bộ {; ; , , }. 
 III. CÁC THUẬT TOÁN 
A. Thuật toán sinh các item đồng xuất hiện 
 Định nghĩa 4: Tập chiếu của item Ik trên CSDL Ɗ: (Ik)= t Ɗ│Ik t} là tập các giao dịch có chứa item Ik. 
 Định nghĩa 5: Cho Ik I, ta gọi Ik là item hạt nhân. Tập mục Xcooc  I gọi đồng xuất hiện cùng độ phổ biến 
với Ik: Xcooc là itemset xuất hiện cùng item hạt nhân Ik và (Ik) = (Xcooc). Ký hiệu, cooc(Ik) = Xcooc. 
 Ví dụ 2: Cho CSDL như trong Bảng 1. Xem item B là item hạt nhân, ta xác định được itemset đồng xuất hiện 
cùng độ phổ biến với item B là cooc(B) = {A, C, E} và sup(B) = sup(ACE) = 2. 
 Dưới đây là thuật toán sinh các item đồng xuất hiện với từng item trong CSDL giao dịch và lưu trữ vào mảng 
Index_COOC. Mỗi phần tử trong Index_COOC gồm 3 thành phần sau: 
 - Index_COOC[j].item: lưu trữ item hạt nhân thứ j; 
 - Index_COOC[j].sup: lưu trữ độ phổ biến của item hạt nhân thứ j; 
 - Index_COOC[j].cooc: lưu trữ itemset đồng xuất hiện cùng item hạt nhân thứ j dưới dạng bit; 
 Ngoài ra, thuật toán 1 còn thực hiện nén CSDL vào mảng Dataset. 
 Mã giả thuật toán 1. Xây dựng bảng Index_COOC và nén dữ liệu 
 Đầu vào: CSDL 
 Đầu ra: Mảng Index_COOC, mảng Dataset 
 1. Với mỗi phần tử j của mảng Index_COOC thực hiện: 
 2. Index_COOC [j].item = Ij 
 3. Index_COOC [j].sup = 0 
 4. Index_COOC [j].cooc= 2m - 1 
 5. Với mỗi giao dịch Ti thực hiện: 
 6. Nén giao dịch Ti vào mảng Dataset 
 7. Với mỗi item j có trong giao dịch Ti thực hiện: 
 8. Index_COOC [j].cooc = Index_COOC [j].cooc & vectorbit(Ti) 
 9. Index_COOC [j].sup = Index_COOC [j].sup + 1 
 10. Sắp xếp mảng Index_COOC tăng dần theo sup 
 11. Trả về mảng Index_COOC, mảng Dataset 
 Từ dòng 1 đến dòng 4 là các bước khởi tạo cho mảng Index_COOC. Dòng 5 duyệt CSDL, ứng với từng giao 
dịch ta xem xét có chứa item thứ j thì thực hiện phép toán AND trên bit để xác định các phần tử cùng xuất hiện với 
item j. Sau cùng, dòng 10 và 11 là sắp xếp mảng Index_COOC tăng dần theo độ phổ biến của item và trả về. 
 Khởi tạo mảng Index_COOC: (thành phần cooc được biểu diễn dạng bit) số item là m = 8 
 item A B C D E F G H 
 sup 0 0 0 0 0 0 0 0 
 cooc 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 
 Đọc giao dịch T1: {A, C, E, F} có biểu diễn dạng bit là 10101100 
 item A B C D E F G H 
 sup 1 0 1 0 1 1 0 0 
 cooc 10101100 11111111 10101100 11111111 10101100 10101100 11111111 11111111 
 Đọc giao dịch T2: {A, C, G} có biểu diễn dạng bit là 10100010 
 item A B C D E F G H 
 sup 2 0 2 0 1 1 1 0 
 cooc 10100000 11111111 10100000 11111111 10101100 10101100 10100010 11111111 
Lê Hoài Bắc, Phan Thành Huấn 725 
 Đọc giao dịch T3: {E, H} có biểu diễn dạng bit là 00001001 
 item A B C D E F G H 
 sup 2 0 2 0 2 1 1 1 
 cooc 10100000 11111111 10100000 11111111 00001000 10101100 10100010 00001001 
 Đọc giao dịch T4: {A, C, D, F, G} có biểu diễn dạng bit là 10110110 
 item A B C D E F G H 
 sup 3 0 3 1 2 2 2 1 
 cooc 10100000 11111111 10100000 10110110 00001000 10100100 10100010 00001001 
 Đọc giao dịch T5: {A, C, E, G} có biểu diễn dạng bit là 10101010 
 item A B C D E F G H 
 sup 4 0 4 1 3 2 3 1 
 cooc 10100000 11111111 10100000 10110110 00001000 10100100 10100010 00001001 
 Đọc giao dịch T6: {E} có biểu diễn dạng bit là 00001000 
 item A B C D E F G H 
 sup 4 0 4 1 4 2 3 1 
 cooc 10100000 11111111 10100000 10110110 00001000 10100100 10100010 00001001 
 Đọc giao dịch T7: {A, B, C, E} có biểu diễn dạng bit là 11101000 
 item A B C D E F G H 
 sup 5 1 5 1 5 2 3 1 
 cooc 10100000 11101000 10100000 10110110 00001000 10100100 10100010 00001001 
 Đọc giao dịch T8: {A, C, D} có biểu diễn dạng bit là 10110000 
 item A B C D E F G H 
 sup 6 1 6 2 5 2 3 1 
 cooc 10100000 11101000 10100000 10110000 00001000 10100100 10100010 00001001 
 Đọc giao dịch T9: {A, B, C, E, G} có biểu diễn dạng bit là 11101010 
 item A B C D E F G H 
 sup 7 2 7 2 6 2 4 1 
 cooc 10100000 11101000 10100000 10110000 00001000 10100100 10100010 00001001 
 Đọc giao dịch T10: {A, C, E, F, G} có biểu diễn dạng bit là 10101110 
 item A B C D E F G H 
 sup 8 2 8 2 7 3 5 1 
 cooc 10100000 11101000 10100000 10110000 00001000 10100100 10100010 00001001 
 Thuật toán 1, trả về mảng Index_COOC tương ứng là cooc(A) = {C}, cooc(B) = {A, C, E}, cooc(C) = {A}, 
cooc(D) = {A, C}, cooc(E) = {}, cooc(F) = {A, C}, cooc(G) = {A, C} và cooc(H) = {E}. 
 Bảng 5. Trả về mảng Index_COOC sắp tăng theo độ phổ biến của item 
 item H B D F G E A C 
 sup 1 2 2 3 5 7 8 8 
 cooc E A, C, E A, C A, C A, C Ø C A 
 Bảng 5, mảng Index_COOC được sắp theo độ phổ biến của từng item (minh họa thành phần cooc theo item). 
B. Thuật toán khai thác tập phổ biến tối đại LA-MFI 
 Theo khảo sát, hầu hết các thuật toán khai thác tập phổ biến tối đại đã được các tác giả trên thế giới đề xuất [5, 
6, 7] đều có nhược điểm lớn và không thực tế: mỗi lần cần khai thác tập phổ biến tối đại với minsup khác thì thuật toán 
thực hiện tính toán lại độ phổ biến của các tập mục, phát sinh lại cây tìm kiếm hoặc dàn tập mục tương ứng và xác định 
tập phổ biến tối đại thỏa minsup mới. Trong thực tế, khi cần khai thác luật kết hợp thì người dùng có thể yêu cầu thực 
hiện khai thác luật kết hợp thỏa ngưỡng minsup và minconf trong nhiều chuỗi thao tác liên tiếp nhau. Các thuật toán đã 
được các tác giả trên thế giới chưa đáp ứng nhu cầu thực tế. 
 Nhóm tác giả đã xây dựng thuật toán LA-MFI khai thác tập phổ biến tối đại dựa trên mảng Index_COOC chứa 
tất cả các itemset đồng xuất hiện của tất cả item trong CSDL có thể thực hiện chuỗi khai thác nhanh tập MFI. 
 Mã giả thuật toán 2. LA-MFI khai thác tập phổ biến tối đại 
 Đầu vào: mảng Index_COOC, minsup, maxsup (độ phổ biến lớn nhất của các item) 
 Đầu ra: Tập phổ biến tối đại MFI 
 1. Với mỗi item thỏa minsup, xem xét: 
726 THUẬT TOÁN HIỆU QUẢ KHAI THÁC TẬP PHỔ BIẾN TỐI ĐẠI TRÊN CƠ SỞ DỮ LIỆU GIAO DỊCH LỚN 
 2. Nếu sup(item) = minsup thì 
 3. MFI = MFI  item cooc (item)} 
 4. Ngược lại 
 5. Nếu (cooc(item) = Ø và sup (item) = maxsup) thì 
 6. MFI= MFI {item} 
 7. Ngược lại 
 8. Tìm tập item Jk thỏa: 
 9. 
 sup( J k ) sup(item )
 J k I \ {item cooc(item )}
 10. Tập * = {sinh các tập phổ biến tối đại từ Jk có sup (k_item) minsup} 
 11. mfi = item cooc(item)}{ f *} 
 12. MFI = MFI mfi 
 13. Trả về tập phổ biến tối đại MFI 
 Ví dụ 3: Cho CSDL như trong Bảng 1 và minsup = 2 
 Item B, D có sup(B) = sup(D) = minsup = 2 (điều kiện dòng 2): 
 Xét item B, có cooc (B) = {A, C, E}, sinh tập mục phổ biến tối đại là (BACE, 2). Lúc này, MFI ={(BACE, 2)}. 
Xét item D – có cooc (D) = {A, C}, sinh tập mục phổ biến tối đại là (DAC,2), MFI ={(BACE, 2), (DAC, 2)}. 
 Xét item F (ngược lại - dòng 7), lúc này item F – cooc(F) = {A, C} còn item G, E, A và C có sup > minsup = 2. 
Tập Jk ={G, E}, sinh tập phổ biến *={G, E, GE}. Tập mục phổ biến tối đại sinh ra trong bước này là mfi = {(FACE, 
2), (FACG, 2)}. Kết thúc bước này, ta có MFI={(BACE, 2), (DAC, 2), (FACE, 2), (FACG, 2)}. 
 Xét item G (ngược lại - dòng 7), lúc này item G – cooc(G) = {A, C} chỉ còn item E có sup(E) = 7 > minsup = 2. 
Tập Jk ={E}, sinh tập phổ biến *={E}. Tập mục phổ biến tối đại sinh ra trong bước này là mfi = {(GACE, 3)}. Kết 
thúc bước này, có MFI={(BACE, 2), (DAC, 2), (FACE, 2), (FACG, 2), (GACE, 3)}. 
 Xét item E, có cooc(E) = { } còn item A và C có sup(A) = sup(C) = 8 > minsup. Tập Jk ={A, C}, sinh tập phổ 
biến *={A, C, AC}. Tập mục phổ biến tối đại sinh ra trong bước này là mfi = {(ACE, 5)} mà ACE  BACE trong 
MFI, nên không đưa mfi ={(ACE, 5)} vào MFI. 
 Sau cùng, chỉ còn item A và C: sinh tập mục phổ biến tối đại (AC, 8), mà AC  BACE, nên không thêm vào 
MFI. 
 Với CSDL ở Bảng 1 và minsup = 2, ta có: MFI={(BACE, 2), (DAC, 2), (FACE, 2), (FACG, 2) 
(GACE, 4)}. 
 IV. KẾT QUẢ THỰC NGHIỆM 
 Thực nghiệm trên máy tính Panasonic CF-74, Core Duo 2.0 GHz, 2GB RAM, thuật toán cài đặt trên C#, 
Microsoft Visual Studio 2010. 
 Nghiên cứu thực nghiệm trên hai nhóm dữ liệu: 
 Nhóm CSDL thực cỡ trung: sử dụng CSDL thực từ kho dữ liệu về học máy của Trường Đại học California 
(Lichman, M. (2013). UCI Machine Learning Repository []. Irvine, CA: University of 
California, School of Information and Computer Science) gồm 2 tập Pumsb và Retail. 
 Nhóm CSDL giả lập cỡ lớn: sử dụng phần mềm phát sinh dữ liệu giả lập của trung tâm nghiên cứu IBM 
Almaden (IBM Almaden Research Center, San Joe, California 95120, U.S.A []) gồm 2 
tập T40I10D100K và T40I10D200K. 
 Bảng 6. Kích thước và tỷ lệ nén trên các tập CSDL thực nghiệm 
 Dung Số Kích thước dữ Tỷ lệ nén 
 Tên CSDL Số item 
 lượng giao dịch liệu sau nén dữ liệu 
 Pumsb 16,30Mb 49.046 2.113 28,08Kb 99,8% 
 Retail 4,07Mb 88.162 16.470 66,61Kb 98,4% 
 T40I1KD100K 15,30Mb 100.000 1.000 83,33Kb 99,5% 
 T40I1KD200K 30,50Mb 200.000 1.000 197,27Kb 99,4% 
Lê Hoài Bắc, Phan Thành Huấn 727 
 (a) Pumsb (b) Retail
 100.00 8
 7
 80.00
 6
 60.00 5
 4
 LA-MFI LA-MFI
 40.00 3
 Thời Thời gian (giây)
 Thời Thời gian (giây) GenMax 2 GenMax
 20.00
 1
 0.00 0
 70% 75% 80% 85% 90% 0.1% 0.2% 0.3% 0.4% 0.5%
 Minsup(%) Minsup(%)
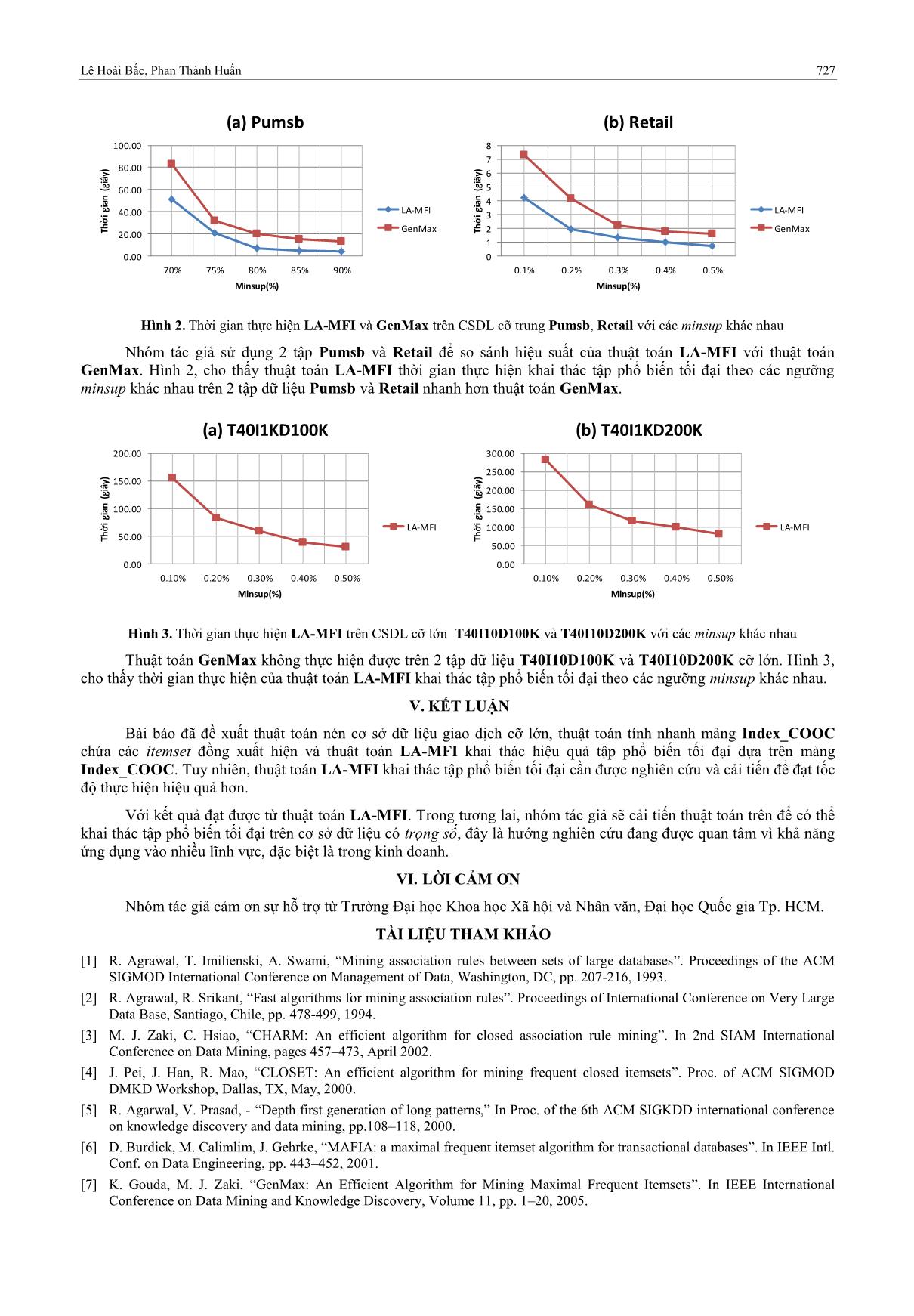
 Hình 2. Thời gian thực hiện LA-MFI và GenMax trên CSDL cỡ trung Pumsb, Retail với các minsup khác nhau 
 Nhóm tác giả sử dụng 2 tập Pumsb và Retail để so sánh hiệu suất của thuật toán LA-MFI với thuật toán 
GenMax. Hình 2, cho thấy thuật toán LA-MFI thời gian thực hiện khai thác tập phổ biến tối đại theo các ngưỡng 
minsup khác nhau trên 2 tập dữ liệu Pumsb và Retail nhanh hơn thuật toán GenMax. 
 (a) T40I1KD100K (b) T40I1KD200K
 200.00 300.00
 250.00
 150.00
 200.00
 100.00 150.00
 LA-MFI 100.00 LA-MFI
 Thời Thời gian (giây)
 Thời Thời gian (giây) 50.00
 50.00
 0.00 0.00
 0.10% 0.20% 0.30% 0.40% 0.50% 0.10% 0.20% 0.30% 0.40% 0.50%
 Minsup(%) Minsup(%)
 Hình 3. Thời gian thực hiện LA-MFI trên CSDL cỡ lớn T40I10D100K và T40I10D200K với các minsup khác nhau 
 Thuật toán GenMax không thực hiện được trên 2 tập dữ liệu T40I10D100K và T40I10D200K cỡ lớn. Hình 3, 
cho thấy thời gian thực hiện của thuật toán LA-MFI khai thác tập phổ biến tối đại theo các ngưỡng minsup khác nhau. 
 V. KẾT LUẬN 
 Bài báo đã đề xuất thuật toán nén cơ sở dữ liệu giao dịch cỡ lớn, thuật toán tính nhanh mảng Index_COOC 
chứa các itemset đồng xuất hiện và thuật toán LA-MFI khai thác hiệu quả tập phổ biến tối đại dựa trên mảng 
Index_COOC. Tuy nhiên, thuật toán LA-MFI khai thác tập phổ biến tối đại cần được nghiên cứu và cải tiến để đạt tốc 
độ thực hiện hiệu quả hơn. 
 Với kết quả đạt được từ thuật toán LA-MFI. Trong tương lai, nhóm tác giả sẽ cải tiến thuật toán trên để có thể 
khai thác tập phổ biến tối đại trên cơ sở dữ liệu có trọng số, đây là hướng nghiên cứu đang được quan tâm vì khả năng 
ứng dụng vào nhiều lĩnh vực, đặc biệt là trong kinh doanh. 
 VI. LỜI CẢM ƠN 
 Nhóm tác giả cảm ơn sự hỗ trợ từ Trường Đại học Khoa học Xã hội và Nhân văn, Đại học Quốc gia Tp. HCM. 
 TÀI LIỆU THAM KHẢO 
[1] R. Agrawal, T. Imilienski, A. Swami, “Mining association rules between sets of large databases”. Proceedings of the ACM 
 SIGMOD International Conference on Management of Data, Washington, DC, pp. 207-216, 1993. 
[2] R. Agrawal, R. Srikant, “Fast algorithms for mining association rules”. Proceedings of International Conference on Very Large 
 Data Base, Santiago, Chile, pp. 478-499, 1994. 
[3] M. J. Zaki, C. Hsiao, “CHARM: An efficient algorithm for closed association rule mining”. In 2nd SIAM International 
 Conference on Data Mining, pages 457–473, April 2002. 
[4] J. Pei, J. Han, R. Mao, “CLOSET: An efficient algorithm for mining frequent closed itemsets”. Proc. of ACM SIGMOD 
 DMKD Workshop, Dallas, TX, May, 2000. 
[5] R. Agarwal, V. Prasad, - “Depth first generation of long patterns,” In Proc. of the 6th ACM SIGKDD international conference 
 on knowledge discovery and data mining, pp.108–118, 2000. 
[6] D. Burdick, M. Calimlim, J. Gehrke, “MAFIA: a maximal frequent itemset algorithm for transactional databases”. In IEEE Intl. 
 Conf. on Data Engineering, pp. 443–452, 2001. 
[7] K. Gouda, M. J. Zaki, “GenMax: An Efficient Algorithm for Mining Maximal Frequent Itemsets”. In IEEE International 
 Conference on Data Mining and Knowledge Discovery, Volume 11, pp. 1–20, 2005. 
728 THUẬT TOÁN HIỆU QUẢ KHAI THÁC TẬP PHỔ BIẾN TỐI ĐẠI TRÊN CƠ SỞ DỮ LIỆU GIAO DỊCH LỚN 
[8] Y. Djenouri, A. Bendjoudi, D. Djenouri, Z. Habbas, “Parallel Processing and Applied Mathematics”, ISBN 978-3-319-32148-6, 
 pp. 258-268, 2016. 
 AN EFFICIENT MINING ALGORITHM FOR MAXIMAL FREQUENT 
 ITEMSETS IN A LARGE TRANSACTIONAL DATABASES 
 Le Hoai Bac, Phan Thanh Huan 
ABSTRACT— Association rule mining, one of the most important and well-researched techniques of Data Mining. Mining maximal 
frequent itemsets is one of the most fundamental problems in association rule mining. According to the survey, most of the 
algorithms in literature used to find minimal frequent item first, then with the help of minimal frequent itemsets derive the maximal 
frequent itemsets. These methods consume more time to find maximal frequent itemsets. To overcome this problem, we propose a 
new approach to fast dectect maximal frequent itemsets using: efficient compression algorithm a large transactional databases and 
array co-occurrence items of kernel item. Finally, we present result, which shows the proposed algorithm has better than the 
existing algorithms. 
Keywords— Association rule mining, co-occurrence items, large transactional databases, maximal frequent itemsets.