Sự hội tụ của dãy lặp kiểu Agarwal đến điểm bất động chung của hai ánh xạ - Không giãn suy rộng trong không gian Banach lồi đều

n suy rộng. n 
 Trước hết, chúng tôi thiết lập một số tính 3 
 limsup ||xn Tx n || limsup || x n p ||
chất của dãy lặp (2.1). nn 1 
 Mệnh đề 2.1. Cho E là không gian limsup ||xpn ||
Banach, K là tập lồi đóng khác rỗng của E , n 
TSKK,: là hai ánh xạ -không giãn suy r( p ,{ xn }). (2.4) 
 Lập luận tương tự, ta chứng minh được 
rộng sao cho FFTFS ()(),   dãy {}xn 
 r( Sp ,{ xnn }) r ( p ,{ x }). (2.5) 
xác định bởi (2.1). Khi đó, {}xn là dãy bị chặn 
 Khi đó, từ (2.4), (2.5) và định nghĩa bán 
và lim ||xpn || tồn tại với pF . 
 n kính tiệm cận của dãy {}xn đối với K, ta suy ra 
 Chứng minh. Với pF , sử dụng Mệnh đề 
 r( Tp ,{ xnn }) r ( K ,{ x }) và 
1.2, ta có r( Sp ,{ x }) r ( K ,{ x }). 
 ||yp || nn
 n Suy ra Tp A( K ,{ x }) và Sp A( K ,{ x }). 
 || (1 )x Tx p || n n
 n n n n Sử dụng tính duy nhất của tâm tiệm cận của dãy 
 (1 n ) ||x n p || n || Tx n p || 
 {}xn đối với K, ta có Tp Sp p hay 
 (1 n ) ||x n p || n || x n p || p F F( T )  F ( S ). Do đó F . 
 ||xpn || . (2.2) Ngược lại, giả sử F . Khi đó, tồn tại 
 Sử dụng Mệnh đề 1.2 và (2.2), ta có pF . Theo Mệnh đề 2.1, ta có {}xn là dãy bị 
 ||xp ||
 n 1 chặn và lim ||xpn || tồn tại. Đặt 
 n 
 || (1 n )Tx n n Sy n p ||
 lim ||xn p || c . (2.6) 
 n 
 (1 n ) ||Tx n p || n || Sy n p || 
 Khi đó, từ (2.2) và (2.6) ta được 
 (1 n ) ||x n p || n || y n p || 
72 
TRÖÔØNG ÑAÏI HOÏC ÑOÀNG THAÙP Taïp chí Khoa hoïc soá 37 (04-2019) 
 limsup ||yn p || c . (2.7) Khi đó, kết hợp bất đẳng thức 
 n ||x y || || x Tx || || Tx Sy || || Sy y ||
 Do T và S là các ánh xạ -không giãn n n n n n n n n
 với (2.11), (2.14) và (2.16), ta được 
suy rộng nên theo Mệnh đề 1.2, ta có 
 lim ||xynn || 0. (2.17)
||Txnn p || || x p ||, ||Synn p || || y p ||. (2.8) n 
 Khi đó, kết hợp (2.8) với (2.6) và (2.7), ta được Mặt khác, từ Bổ đề 1.3, ta có 
 ||x Sx ||
limsup ||Txn p || c , limsup ||Syn p || c . (2.9) nn
 n n ||x y || || y Sx ||
 Hơn nữa, n n n n
 3 
c lim || xn 1 p || ||x y || || y Sy || || y x || 
 n n n1 n n n n
 lim || (1 n )Tx n n Sy n p || 
 n 3 
 2 ||xn y n || || y n Sy n || . (2.18)
 lim || (1 n )(Tx n p ) n ( Sy n p ) || . (2.10) 1 
 n Do đó, từ (2.16), (2.17) và (2.18), ta được 
 Khi đó, từ (2.9), (2.10) và sử dụng Bổ đề 
 lim ||xnn Sx || 0 . 
1.7 ta có n 
 lim ||Synn Tx || 0. (2.11) Tiếp theo, chúng tôi thiết lập sự hội tụ yếu 
 n của dãy lặp (2.1) đến điểm bất động chung của 
 Hơn nữa, kết hợp đẳng thức 
 hai ánh xạ -không giãn suy rộng. 
||x Tx ||  || Tx Sy || với (2.11), ta được 
 n 1 n n n n Định lí 2.3. Cho E là không gian Banach 
 lim ||xnn 1 Tx || 0. (2.12) 
 n lồi đều và có tính chất Opial, K là tập lồi đóng 
 Khi đó, kết hợp bất đẳng thức khác rỗng của E, TSKK,: là hai ánh xạ 
 -không giãn suy rộng sao cho F , dãy 
||xn 11 Sy n || || x n Tx n || || Tx n Sy n || với 
 {}xn xác định bởi (2.1). Khi đó, dãy {}xn hội tụ 
(2.11) và (2.12), ta được lim ||xnn 1 Sy || 0. 
 n yếu đến pF . 
Kết hợp điều này với (2.6) và bất đẳng thức 
 Chứng minh. Từ Mệnh đề 2.2, ta có dãy 
 ||xn 11 p || || x n Sy n || || Sy n p || 
 {}xn bị chặn và 
 ||xn 1 Sy n || || y n p ||, 
 lim ||xn Tx n || lim || x n Sx n || 0. 
 nn 
ta được c liminf || yn p ||. Khi đó, từ (2.7) ta 
 n Vì E là không gian Banach lồi đều nên E 
được lim ||yn p || c . Do đó, là không gian Banach phản xạ. Khi đó, tồn tại 
 n 
 dãy con {}xni() của {}xn sao cho {}xni() hội tụ 
c lim || yn p ||
 n yếu đến pK . Do đó, 
 lim || (1 n )x n n Tx n p || 
 n lim ||Txn()()()() i x n i || lim || Sx n i x n i || 0. 
 ii 
 lim || (1 n )(x n p ) n ( Tx n p ) || . (2.13)
 n Khi đó, sử dụng Mệnh đề 1.10, ta có 
 Khi đó, từ (2.6), (2.9), (2.13) và sử dụng Bổ Tp Sp p hay p F F( T )  F ( S ). Tiếp 
đề 1.7, ta được theo, ta giả sử {}xn không hội tụ yếu đến p. Khi 
 lim ||Txnn x || 0. (2.14) 
 n đó, tồn tại dãy con {}xnk() của {}xn sao cho 
 Hơn nữa, {}xnk() hội tụ yếu đến qK với pq . Lập 
 ||Sy y ||
 nn luận tương tự như trên, từ Mệnh đề 1.10, ta có 
 ||Sy [(1 ) x Tx ]||
 n n n n n qF . Hơn nữa, theo Mệnh đề 2.1, ta có 
 ||Syn x n || n || x n Tx n || lim ||xpn || và lim ||xqn || tồn tại. Sử dụng 
 n n 
 ||Syn Tx n || || Tx n x n || n || x n Tx n || . (2.15) tính chất Opial, ta có 
Từ (2.11), (2.14) và (2.15), ta được 
 lim ||Synn y || 0. (2.16) 
 n 
 73 
TRÖÔØNG ÑAÏI HOÏC ÑOÀNG THAÙP Taïp chí Khoa hoïc soá 37 (04-2019) 
lim ||xn p || liminf || x n() i p || Định lí 2.5. Cho E là không gian Banach 
ni lồi đều, K là tập lồi đóng khác rỗng của E, 
 liminf ||xqni() || 
 i TSKK,: là hai ánh xạ -không giãn suy 
 lim ||xn q || liminf || x n() k q || rộng sao cho F , thỏa mãn điều kiện ()B và 
 nk 
 dãy {}xn xác định bởi (2.1). Khi đó, dãy {}xn hội 
 liminf ||xn() k p || lim || x n p ||. 
 kn tụ mạnh đến pF . 
 Điều này là một mâu thuẫn. Do đó, pq . 
 Chứng minh. Từ Mệnh đề 2.2, ta có 
Vậy {}xn hội tụ yếu đến pF . 
 lim ||Txn x n || lim || Sx n x n || 0. (2.19) 
 Tiếp theo, chúng tôi thiết lập một số kết nn 
quả về sự hội tụ mạnh của dãy lặp (2.1) đến Vì T và S thỏa mãn điều kiện B nên tồn 
điểm bất động chung của hai ánh xạ -không tại hàm không giảm f :[0, ) [0, ) sao cho 
giãn suy rộng. f (0) 0 và fr( ) 0 với mọi r 0 và 
 Định lí 2.4. Cho E là không gian Banach, 
 max{||xn Tx n ||,|| x n Sx n ||} f ( d ( x n , F )). (2.20)
K là tập lồi đóng khác rỗng của E , Khi đó, từ (2.19) và (2.20), ta được 
TSKK,: là hai ánh xạ -không giãn suy 
 limf ( d ( xn , F )) 0. Giả sử limd ( xn , F ) 0. 
 n n 
rộng với F , dãy {}xn xác định bởi (2.1) và 
 Khi đó, với  0, tồn tại n0 sao cho với 
liminfd ( xn , F ) 0. Khi đó, dãy {}xn hội tụ 
 n mọi nn , ta có d(,). x F  Khi đó, 
mạnh đến pF . 0 n
 f( d ( xn , F )) f ( ). Do đó limf ( d ( xn , F )) f ( ) 0. 
 Chứng minh. Với pF , theo Mệnh đề n 
 Điều này mâu thuẫn với limf ( d ( x , F )) 0. Do 
2.1, ta có lim ||xpn || tồn tại. Do đó, n
 n n 
 đó, limd ( x , F ) 0. Khi đó, theo Định lí 2.4, ta 
limd ( xnn , F ) liminf {|| x p ||, p F } tồn tại. n
nn n 
 suy ra {}x hội tụ mạnh đến pF . 
Khi đó, limd ( xnn , F ) liminf d ( x , F ) 0. Khi n
 nn Định lí 2.6. Cho E là không gian Banach 
đó, tồn tại dãy con {}x của {}x và với dãy 
 nk() n lồi đều, K là tập lồi đóng khác rỗng của 
 k
{},pFk  ta có ||xpn() k k || 2 . Khi đó, theo E ,TSKK,: là hai ánh xạ -không giãn 
bất đẳng thức (2.3), ta được suy rộng sao cho F , T hoặc S là nửa 
 k
 compact và dãy {}xn xác định bởi (2.1). Khi đó, 
 ||xn( k 1) p k || || x n ( k ) p k || 2 . 
Điều này dẫn đến dãy {}xn hội tụ mạnh đến xF . 
||p p || || p x || || x p || Chứng minh. Theo Định lí 2.3, ta có {}x 
 k 1 k k 1 n ( k 1) n ( k 1) k n
 (k 1) k ( k 1)
 bị chặn và lim ||Txn x n || lim || Sx n x n || 0. 
 2 2 2 . nn 
Suy ra {}pk là dãy Cauchy trong F. Hơn nữa, Hơn nữa, vì T hoặc S là nửa compact nên tồn 
theo Bổ đề 1.6, ta có FFTFS ()() là tập 
 tại dãy con {}xnk() của {}xn sao cho {}xnk() hội 
đóng trong không gian Banach hay F có tính tụ đến pK . Mặt khác, từ Bổ đề 1.3, ta có 
đầy đủ. Do đó, dãy {}p hội tụ mạnh đến pF . 
 k 3 
Hơn nữa, từ ||xn()()()() k Tp || || x n k Tx n k || || x n k p || . 
 1 
 ||xn()() k p || || x n k p k || || p k p ||
 Điều này dẫn đến lim ||xnk() Tp || 0 hay 
 k k 
 2 ||ppk ||,
 dãy {}xnk() hội tụ đến Tp. Sử dụng tính duy nhất 
 ta có lim ||xpnk() || 0. Kết hợp với giới hạn 
 k của giới hạn, ta có T(). p p Lập luận tương tự, 
lim ||xpn || tồn tại, ta suy ra {}xn hội tụ mạnh ta chứng minh được S(). p p Vì vậy pF . 
n 
đến pF . 
74 
TRÖÔØNG ÑAÏI HOÏC ÑOÀNG THAÙP Taïp chí Khoa hoïc soá 37 (04-2019) 
Do đó, theo Mệnh đề 2.1, ta có lim ||xpn || tồn Trường hợp 3. Với x (0,1]\{1/ 3}, 
 n 
tại. Suy ra tồn tại giới hạn y 1/ 3 ta có 
 VP 0,5| x (1/3)| 0,5|0 x |
 limd ( xnn , F ) liminf {|| x p ||, p F }. 
 nn 
 0,5[xx (1/ 3)] 0,5
 Mặt khác, vì d( xn()() k , F ) || x n k p || nên 
 x (1/ 6) 
limd ( xnk() , F ) 0. Do đó, limd ( xn , F ) 0. Khi 
k n x
đó, theo Định lí 2.4, ta có dãy {}x hội tụ mạnh 
 n ||Tx Ty || .
đến xF . Trường hợp 4. Với xy, (0,1]\{1/ 3} ta có 
 Cuối cùng, chúng tôi đưa ra ví dụ minh họa VP 0,5 | x y | 0,5 | y x |
cho việc sử dụng kết quả đạt được để chứng tỏ sự 
 |xy |
hội tụ của dãy lặp (2.1) đến điểm bất động chung 
của hai ánh xạ -không giãn suy rộng. Trong |xy |
đó, Ví dụ 2.8 chứng tỏ rằng dãy lặp (2.1) hội tụ ||Tx Ty || .
đến điểm bất động chung của hai ánh xạ không 
 Trường hợp 5. Với x [-1,0], y (0,1]\{1/ 3} 
giãn nhanh hơn dãy lặp (1.5) trong [9]. Lưu ý 
 ta có ||Tx Ty || | ( x / 3) y |, 
rằng, trong hai ví dụ sau, tất cả các tính toán số 
 VP 0,5|(/3) x y | 0,5| y x |
được viết trên phần mềm Scilab-6.0.0. 
 Ví dụ 2.7. Xét E là không gian Banach 0,5[y ( x / 3)] 0,5( x y ) 
với chuẩn giá trị tuyệt tối, K [ 1,1] và hai ánh (xy / 3)
xạ TSKK,: được xác định bởi: nếu và 
 x/ 3 neáu x [-1,0], VP 0,5|(/3) x y | 0,5| y x |
 Tx 0 neáu x 1/ 3, 0,5[y ( x / 3)] 0,5( x y )
 -x neáu x (0,1] \ {1/ 3}, (2x / 3)
 và (xy / 3) .
 x neáu x [-1,0], Do đó, VP |(/3) x y ||| Tx Ty ||. Vậy T 
 Sx 0 neáu x 1/ 2, là ánh xạ -không giãn suy rộng với 0,5. 
 -x / 2 neáu x (0,1] \ {1/ 2}. Lập luận tương tự như trên, ta chứng tỏ 
 Khi đó, T và S là hai ánh xạ -không được S là ánh xạ -không giãn suy rộng với 
giãn suy rộng. Thật vậy, trước hết ta chứng minh 0,5. 
T là ánh xạ -không giãn suy rộng với 0,5. Ta lại có FFTFS ( )  ( ) {0}. Hơn nữa, 
Đặt VP || Tx y || || Ty x || (1 2 ) || x y ||. các giả thiết còn lại trong Định lí 2.3, Định lí 2.4, 
Ta chỉ cần xét các trường hợp sau: Định lí 2.5, Định lí 2.6 cũng thỏa mãn. Do đó, 
 Trường hợp 1. Với xy, [-1,0] ta có dãy {}xn xác định bởi (2.1) hội tụ đến 0 là điểm 
VP 0,5|( x /3) y | 0,5|( y /3) x | bất động chung của ST,. Tuy nhiên, bằng cách 
 0,5 | (x / 3) y ( y / 3) x | chọn x 1/ 3 và y 1 ta có 
 (2 / 3) |x y | (1/ 3) | x y | 0,5||x Tx ||1/6 2/3|| x y || và 
 1
 ||xy ||Tx Ty || 1 2 / 3 || x y ||. 
 3 Tương tự, bằng cách chọn x 0,5 và 
 ||Tx Ty || .
 y 5 / 6 ta có 
 Trường hợp 2. Với xy [-1,0], 1/ 3 ta có 
 0,5||x Sx || 0,25 1/ 3 || x y || và 
VP 0,5|( x /3) (1/3)| 0,5|0 x |
 ||Sx Sy || 5 /12 1/ 3 || x y ||. Điều này dẫn 
 0,5[(1/ 3) (xx / 3)] 0,5 
 (2 / 3)x (1/ 6) đến hai ánh xạ TS, không thỏa mãn điều kiện 
 (1/ 3)x || Tx Ty || . ()C và do đó không là ánh xạ không giãn. Vì 
 75 
TRÖÔØNG ÑAÏI HOÏC ÑOÀNG THAÙP Taïp chí Khoa hoïc soá 37 (04-2019) 
vậy, các kết quả về sự hội tụ của dãy lặp đến mãn. Do đó, theo Định lí 2.6 và [9, Theorem 
điểm bất động chung của ánh xạ không giãn 3.7], dãy {}xn xác định bởi (2.1) và dãy (1.5) 
trong [9] là không áp dụng được cho hai ánh xạ trong [9] hội tụ đến 0 là điểm bất động chung của 
TS, được đưa ra. ST,. Tuy nhiên, với cách chọn x 0,5, 
 Bằng tính toán số, chúng tôi minh họa dáng 1
 n 1 23n 
điệu hội tụ của dãy {}x xác định bởi (2.1) đến 0 và  với n , dãy 
 n n 23n n 34n 
trong hai trường hợp cụ thể sau: 
 {}x xác định bởi (2.1) có dạng 
 n 1 n
 Trường hợp: n 50, x1 0,5 , n 
 23n x1 0,5
 23n ...
và  với n . 
 n 34n 
 nn 12 2 3 , (2.21) 
 xn 1 0,5 x n sin( y n )
 3nn 4 3 4
 nn 21
 y x0,5 x2
 n2nn 3 n 2 3 n
 còn dãy lặp (1.5) trong bài báo [9] có dạng 
 x1 0,5
 ...
 nn 1 2 3 , (2.22) 
 xn 1 x nsin( y n )
 3nn 4 3 4
 nn 212
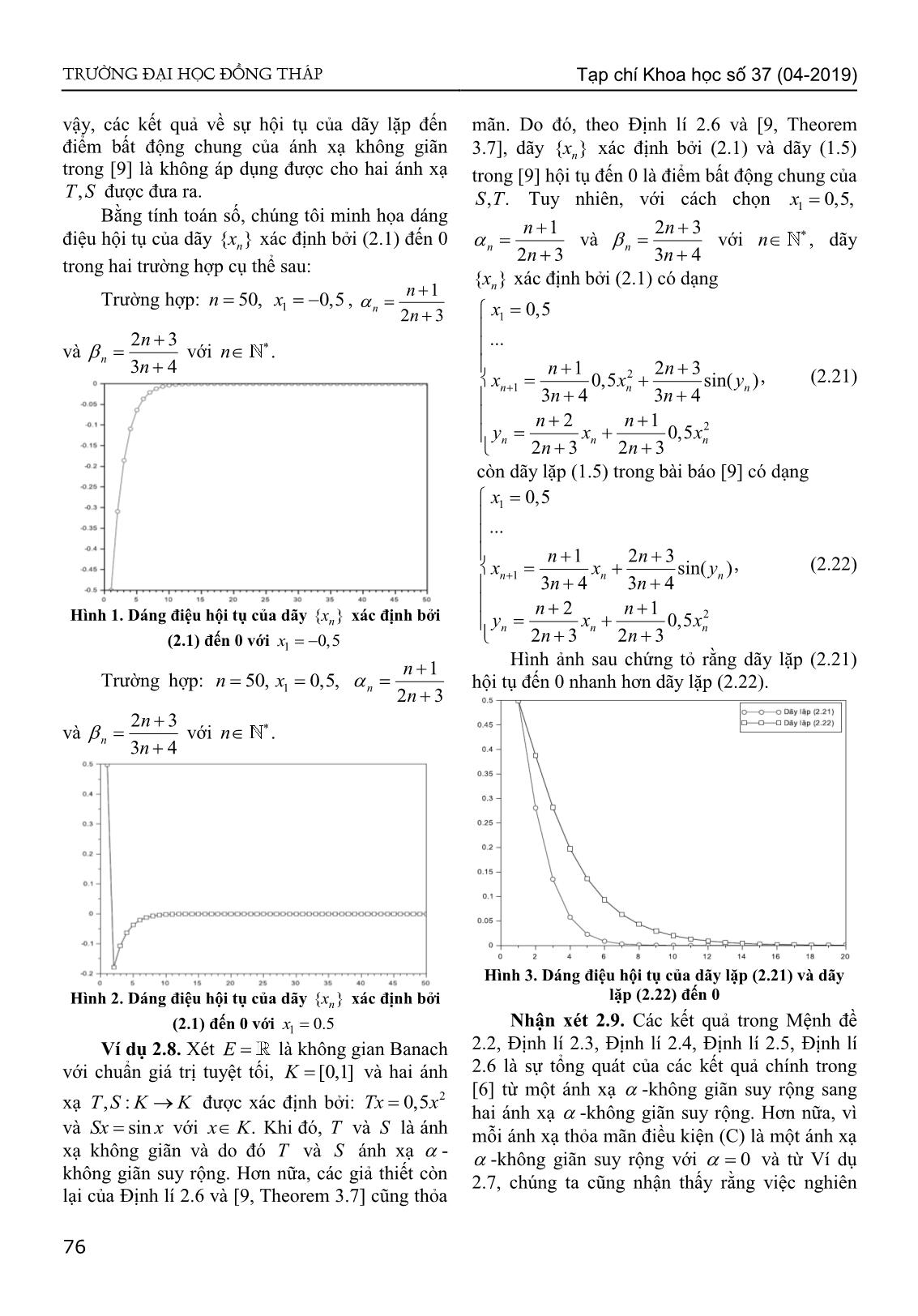
Hình 1. Dáng điệu hội tụ của dãy {}xn xác định bởi y x0,5 x
 n2nn 3 n 2 3 n
 (2.1) đến 0 với x1 0,5 
 n 1 Hình ảnh sau chứng tỏ rằng dãy lặp (2.21) 
 Trường hợp: n 50, x 0,5, hội tụ đến 0 nhanh hơn dãy lặp (2.22). 
 1 n 23n 
 23n 
và  với n . 
 n 34n 
 Hình 3. Dáng điệu hội tụ của dãy lặp (2.21) và dãy 
 lặp (2.22) đến 0 
Hình 2. Dáng điệu hội tụ của dãy {}xn xác định bởi 
 (2.1) đến 0 với x1 0.5 Nhận xét 2.9. Các kết quả trong Mệnh đề 
 Ví dụ 2.8. Xét E là không gian Banach 2.2, Định lí 2.3, Định lí 2.4, Định lí 2.5, Định lí 
với chuẩn giá trị tuyệt tối, K [0,1] và hai ánh 2.6 là sự tổng quát của các kết quả chính trong 
 [6] từ một ánh xạ -không giãn suy rộng sang 
xạ TSKK,: được xác định bởi: Tx 0,5 x2 
 hai ánh xạ -không giãn suy rộng. Hơn nữa, vì 
và Sx sin x với xK . Khi đó, T và S là ánh mỗi ánh xạ thỏa mãn điều kiện (C) là một ánh xạ 
xạ không giãn và do đó T và S ánh xạ - -không giãn suy rộng với 0 và từ Ví dụ 
không giãn suy rộng. Hơn nữa, các giả thiết còn 2.7, chúng ta cũng nhận thấy rằng việc nghiên 
lại của Định lí 2.6 và [9, Theorem 3.7] cũng thỏa 
76 
TRÖÔØNG ÑAÏI HOÏC ÑOÀNG THAÙP Taïp chí Khoa hoïc soá 37 (04-2019) 
cứu sự hội tụ của dãy lặp kiểu Agarwal đến điểm Bài báo này được hỗ trợ bởi Trường Đại 
bất động chung của ánh xạ thỏa mãn điều kiện học Đồng Tháp với Đề tài nghiên cứu khoa học 
(C) là không cần thiết. của sinh viên mã số SPD2018.02.58./. 
 Tài liệu tham khảo 
 [1]. K. Aoyama and F. Kohsaka (2011), “Fixed point theorem for -nonexpansive mapping in 
Banach space”, Nonlinear Anal., (74), pp. 4387-4391. 
 [2]. B. Beauzamy (1982), Introduction to Banach spaces and their geometry, North-Holland 
Mathematics Studies, vol.68, North-Holland, Amsterdam. 
 [3]. F. E. Browder (1965), “Nonexpansive nonlinear operators in a Banach space”, Proc. Nat. 
Acad. Sci. USA, (54), pp. 1041-1044. 
 [4]. E. L. Dozo (1973), “Multivalued nonexpansive mappings and Opial's condition”, Proc. 
Amer. Math. Soc., 38(2), pp. 286-292. 
 [5] K. Goebel and W. A. Kirk (1990), Topics in Metric Fixed Point Theory, Cambridge Studies 
in Advanced Mathematics, vol.28. Cambridge University Press, Cambridge. 
 [6]. R. Pant and R. Shukla (2017), “Approximating fixed points of generalized -nonexpansive 
mappings in Banach spaces”, Numer. Funct. Anal. Optim., 38 (2), pp. 248-266. 
 [7]. H. Piri, B.Daraby, S. Rahrovi and M. Ghasemi (2018), “Approximating fixed points of 
generalized -nonexpansive mappings in Banach spaces by new faster iteration process”, Numer. 
Algorithms, pp. 1-20, first online. 
 [8]. J. Schu (1991), “Weak and strong convergence to fixed points of asymptotically 
nonexpansive mappings”, Bull. Aust. Math. Soc., 43 (1), pp. 153-159. 
 [9]. N. Shahzad and R. Al-Dubiban (2006), “Approximating common fixed points of 
nonexpansive mappings in Banach spaces”, Georgian Math. J., 13 (3), pp. 529-537. 
 [10]. T. Suzuki (2011), “Fixed point theorems and convergence theorems for some generalized 
nonexpansive mappings”, J. Math. Anal. Appl., (340), pp. 1088-1095. 
 CONVERGENCE OF AGARWAL-TYPE ITERATION PROCESS 
 TO COMMON FIXED POINTS OF TWO GENERALIZED -NONEXPANSIVE 
 MAPPINGS IN UNIFORMLY CONVEX BANACH SPACES 
 Summary 
 In this paper, we come up with establishing the weak and strong convergence of Agarwal type 
iteration process to common fixed points of two generalized -nonexpansive mappings in uniformly 
convex Banach spaces. These results are the extensions of the main ones found in [6] and [9]. In 
addition, some examples are provided for illustration. 
 Keywords: Generalized -nonexpansive mapping, Agarwal iteration process, common fixed point. 
 Ngày nhận bài: 20/2/2019; Ngày nhận lại: 16/4/2019; Ngày duyệt đăng: 19/4/2019. 
 77