Sử dụng Geogebra để củng cố lí thuyết hình học

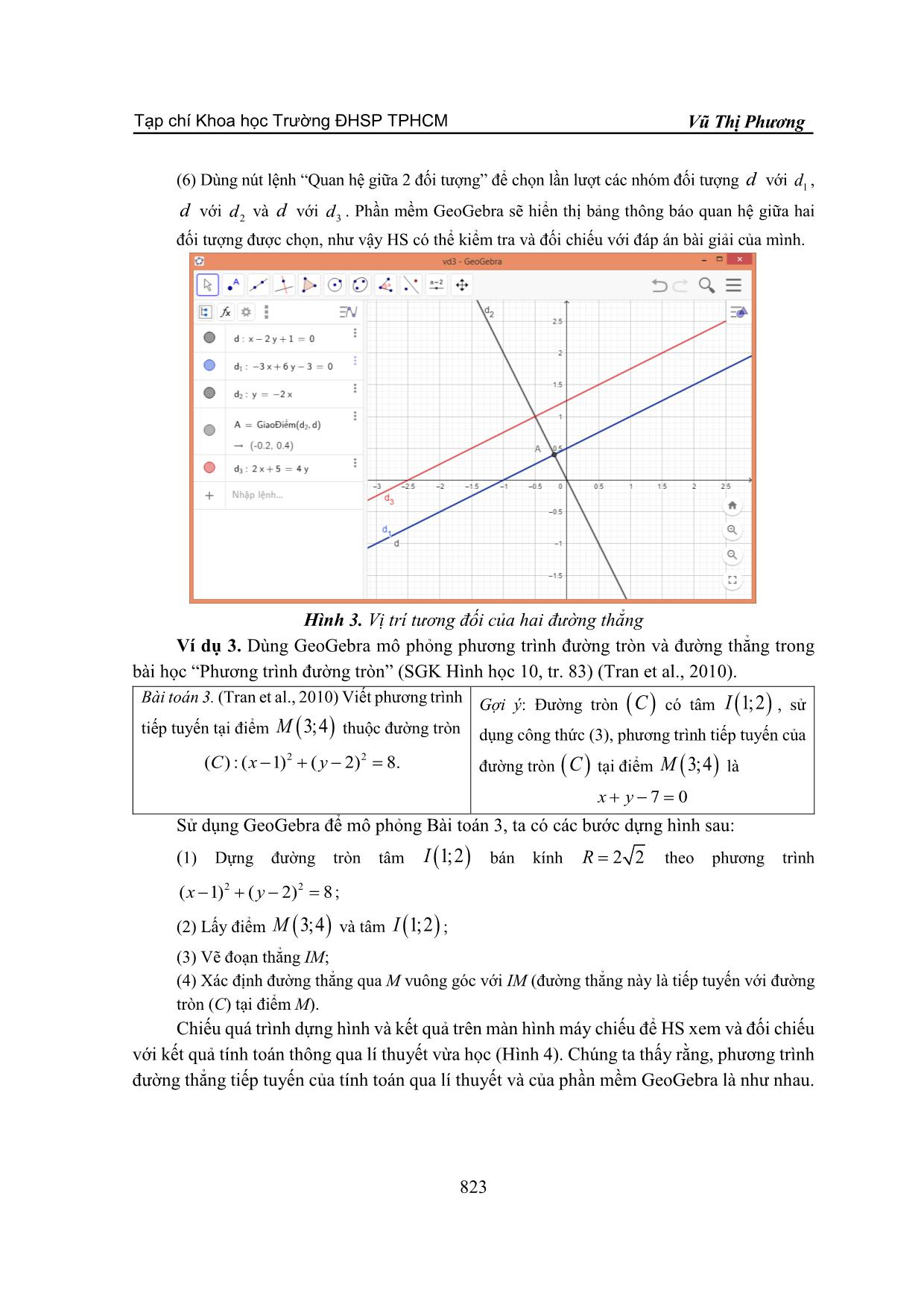
a học đã nghiên cứu về ảnh hưởng của 
việc sử dụng phần mềm GeoGebra đối với việc thúc đẩy việc học Toán ở trường trung học 
và về tác động của nó đối với quan niệm của GV về việc dạy và học Toán (Dockendor, & 
Solar, 2017) 
2. Các kiến thức cơ bản 
Định nghĩa 1. Phương trình ax+ by += c 0 với a và b không đồng thời bằng 0, được gọi là 
phương trình tổng quát của đường thẳng. (Tran et al., 2010). 
 Cho hai đường thẳng d1 và d2 có phương trình tổng quát là ax111+ by += c 0 và
ax222+ by += c 0 . Tọa độ giao điểm của d1 và d2 là nghiệm của hệ phương trình 
 ax111+ by += c 0
  . (1) 
 ax222+ by += c 0
 Ta thấy, hệ (1) xảy ra các trường hợp sau: hệ (1) có một nghiệm khi d1 và d2 cắt nhau; 
hệ (1) có vô số nghiệm khi d1 và d2 trùng nhau; hệ (1) vô nghiệm khi d1 và d2 song song 
với nhau. 
Định lí Côsin. (Tran et al., 2010) Trong tam giác ABC bất kì với BC = a, CA = b, AB = c ta có: 
 a2=+− b 22 c2 bc .cos A ;
 b2=+− a 22 c2 ac .cos B ; (2) 
 c2=+− a 22 b2 ab .cos C .
Định nghĩa 2. Phương trình đường tròn tâm I(a; b) bán kính R là 
 22
 ( xa−) +−( yb) = R2. 
 Cho điểm Mxy000(; ) nằm trên đường tròn (C) có tâm I( ab; ) . Gọi d là tiếp tuyến 
với (C) tại M 0 , d có phương trình là 
 ( x0− axx)( −+− 00) ( y byy)( −= 0) 0 (3) 
 Trong quá trình nghiên cứu và sử dụng, chúng tôi dùng phần mềm GeoGebra phiên 
bản 6.0.620.0-offline được cài đặt trên máy tính cá nhân, ngôn ngữ hiển thị là tiếng Việt. 
 Tính năng cơ bản của GeoGebra được biết đến là: mô tả các điểm, đường/đoạn thẳng; 
vẽ các đa giác, đường tròn, elip, dựng hình đối xứng, quay hình; xác định độ dài đoạn thẳng, 
số đo góc, diện tích đa diện 
 Giao diện GeoGebra chia thành hai phần chính: bên trái là cửa sổ CAS (nhập lệnh) 
còn bên phải là vùng làm việc hay để hiển thị hình (Hình 1). Để hiểu hơn và sử dụng tốt 
phần mềm này, bạn đọc có thể tham khảo tài liệu “Phần mềm GeoGebra 5.0 hướng dẫn sử 
dụng và ứng dụng trong môn toán cấp ba” (bản tiếng Việt) của tác giả Trần Phúc Hòa 
(Tran, 2016). 
 819 
Tạp chí Khoa học Trường ĐHSP TPHCM Tập 18, Số 5 (2021): 817-826 
 Hình 1. Giao diện cơ bản của GeoGebra 
3. Nội dung nghiên cứu 
3.1. Quy trình áp dụng 
 Trong quá trình giảng dạy Hình học lớp 10, chúng tôi thấy rằng, việc áp dụng phần 
mềm GeoGebra vào mỗi bài, mỗi phần, mỗi ví dụ là khác nhau. Với mục tiêu áp dụng để 
củng cố lí thuyết bài học thì sự lựa chọn ví dụ hay bài toán phù hợp để mô phỏng lí thuyết 
của bài học đó là rất quan trọng. 
 Ở đây, chúng tôi không đề cập toàn bộ tiến trình của cả tiết học, mà chỉ đề cập khoảng 
thời gian ngắn sử dụng phần mềm GeoGebra minh họa bài toán để củng cố lí thuyết chính 
của bài học. Trong quá trình giảng dạy thực tế trên lớp, cùng với sự góp ý của các đồng 
nghiệp trong tổ bộ môn và sự tự rút kinh nghiệm của bản thân sau giờ dạy, chúng tôi đã đưa 
ra quy trình hoạt động được áp dụng là: 
 (1) Đưa ra bài toán củng cố: là bài toán điển hình, không quá khó và phù hợp với nội 
dung lí thuyết cần củng cố; 
 (2) HS giải bài toán theo phương pháp lí thuyết vừa học; 
 (3) GV mô phỏng bài toán với phần mềm GeoGebra; 
 (4) HS so sánh, đối chiếu với kết quả: quá trình này xảy ra hai trường hợp: một là, đối 
với HS giải đúng thì điều đó càng củng cố vững chắc niềm tin của HS với sự hiểu bài và sự 
vận dụng lí thuyết; hai là, đối với những HS giải sai hoặc chưa giải xong vì chưa hiểu rõ lí 
thuyết bài học hoặc việc vận dụng lí thuyết vào giải bài tập còn vướng mắc, thì sự mô phỏng 
bài toán với phần mềm GeoGebra giúp HS khắc sâu lí thuyết và bài tập áp dụng một lần nữa, 
từ đó, giúp các em hiểu lí thuyết hơn và tăng kĩ năng vận dụng lí thuyết vào giải toán. 
3.2. Áp dụng thực tiễn 
 Phần mềm GeoGebra giảng dạy thực tế ở 5 lớp khối 10 tại Trường THPT Thực hành 
Cao Nguyên, tỉnh Đắk Lắk. Qua học kì 1 năm học 2020-2021, chúng tôi thấy rằng, việc sử 
dụng GeoGebra để củng cố lí thuyết hình học có hiệu quả và có tác dụng lớn, đặc biệt đối 
với việc giúp HS hiểu và khắc sâu về các định lí, hệ quả. Tuy rằng, định lí về mặt toán học 
đã được chứng minh một cách chặt chẽ, nhưng định lí được nêu ra rất cô đọng và súc tích, 
 820 
Tạp chí Khoa học Trường ĐHSP TPHCM Vũ Thị Phương 
nhiều HS chưa thể tưởng tượng ra hay hiểu và vận dụng được ngay, vì thế HS cần một quá 
trình như giải thích, minh họa, mô phỏng những lí thuyết đó. 
 Trong phần này, chúng tôi sẽ đề cập việc sử dụng GeoGebra để củng cố định lí và lí 
thuyết bài học. 
 a. Củng cố định lí 
 Trong toán học, việc HS nắm bắt và khắc sâu được các định lí là rất quan trọng, nó 
quyết định đến sự vận dụng lí thuyết vào quá trình làm bài tập trong SGK và áp dụng trong 
thực tiễn. Vì vậy, việc dạy một định lí làm sao cho hiệu quả đã được GV quan tâm nghiên 
cứu hay sử dụng phần mềm để minh họa quá trình này (Phan, 2013; Smirnov, 2017). 
 Hoạt động dạy học định lí diễn ra hai giai đoạn: 
 - Chứng minh định lí – quá trình sử dụng các công thức, định lí, kiến thức đã biết để 
trình bày, diễn giải, biến đổi lí thuyết để đi đến điều phải chứng minh; 
 - Củng cố định lí – quá trình GV giúp HS củng cố kiến thức bằng cách mô phỏng thực 
tế để nhận dạng và thể hiện định lí hoặc cho HS làm các bài tập có thể sử dụng định lí vừa 
học để nhận dạng định lí đó. 
 Ví dụ 1. Dùng GeoGebra để mô phỏng và củng cố sự đúng đắn của Định lí Côsin trong 
bài “Các hệ thức lượng trong tam giác và giải tam giác” (SGK Hình học 10, tr. 48) 
(Tran et al., 2010). Chúng ta xem xét bài toán sau: 
 Bài toán 1. (Tran et al., 2010) Cho tam giác Gợi ý: tính toán theo Định lí Côsin (2) ta được: 
 ABC có cạnh a=16 cm , cạnh b=10 cm c≈ 21.6 cm , A = 44 2' và B = 25 58' . 
 và góc C =1100 . Tính độ dài cạnh c và các 
 góc AB, của tam giác đó. 
 Sử dụng GeoGebra để mô phỏng hình trong Bài toán 1 và chiếu lên màn hình để HS 
xem, ta sử dụng các bước dựng hình sau: 
 (1) Vẽ đoạn thẳng với độ dài cố định ( BC=16 cm ); 
 (2) Xác định C’ với độ góc cho trước ( BCC '= 1100 ), ta sẽ có CC'= 16 cm ; 
 (3) Vẽ đường tròn tâm C bán kính 10 cm , xác định điểm A là giao điểm của đường tròn và 
đoạn thẳng CC’, ta được AC=10 cm (sau đó ẩn đường tròn, đoạn CC ' và điểm C '); 
 (4) Vẽ các đoạn thẳng AC và AB ; 
 (5) Xác định ABC và BAC . 
 Cho HS so sánh kết quả tính toán được theo Định lí Côsin với kết quả phần mềm 
GeoGebra xác định được bên cửa sổ CAS (Hình 2). Từ đó, HS xác nhận, tin tưởng vào công 
thức tính toán của Định lí Côsin và bản thân. 
 821 
Tạp chí Khoa học Trường ĐHSP TPHCM Tập 18, Số 5 (2021): 817-826 
 Hình 2. Minh họa tính toán theo cố Định lí Côsin 
 b. Củng cố lí thuyết bài học 
 Việc nắm vững lí thuyết bài học môn Toán đối với HS là rất cần thiết, bởi các định 
nghĩa, tính chất, công thức là rất quan trọng, HS phải nhớ thì mới vận dụng được để giải 
quyết các bài tập. Để củng cố lí thuyết, GV thường giao các bài tập áp dụng lí thuyết vừa 
mới học. 
 Ví dụ 2. Để củng cố lí thuyết đường thẳng, chúng ta xem xét mục “5. Vị trí tương đối 
của các đường thẳng” trong bài “Phương trình đường thẳng” (SGK Hình học 10, tr.78) (Tran 
et al., 2010). Chúng ta xem xét bài tập hoạt động của HS trên lớp: 
 Bài toán 2. Xét vị trí tương đối của đường thẳng Gợi ý: Sử dụng lí thuyết vị trí tương đối của các 
 dx:− 2 y += 10 với mỗi đường thẳng sau: đường thẳng trong (1) để giải. Hoặc giải tương 
 tự như ví dụ đã nêu ở trong SGK. Đáp án: 
 d1 :− 3 xy + 6 −= 3 0;
 dd≡ ; d cắt d tại điểm (−0,2; 0,4) và 
 dy2 := − 2; x 1 2
 dx3 :2+= 5 4 y . dd// 3 . 
 Sử dụng GeoGebra để mô phỏng Bài toán 2, chúng ta có các bước dựng hình sau: 
 (1) Nhập phương trình d trong cửa sổ CAS; 
 (2) Nhập phương trình d1 trong cửa sổ CAS; 
 (3) Nhập phương trình d2 trong cửa sổ CAS; 
 (4) Xác định giao điểm A của đường thẳng d và d2 ; 
 (5) Nhập phương trình d3 trong cửa sổ CAS; 
 Chờ HS làm bài xong, GV chiếu quá trình dựng hình và kết quả trên màn hình máy 
chiếu để HS xem và đối chiếu với kết quả tính toán (Hình 3). Sau đó GV thực hiện 
bước sau: 
 822 
Tạp chí Khoa học Trường ĐHSP TPHCM Vũ Thị Phương 
 (6) Dùng nút lệnh “Quan hệ giữa 2 đối tượng” để chọn lần lượt các nhóm đối tượng d với d1 , 
 d với d2 và d với d3 . Phần mềm GeoGebra sẽ hiển thị bảng thông báo quan hệ giữa hai 
 đối tượng được chọn, như vậy HS có thể kiểm tra và đối chiếu với đáp án bài giải của mình. 
 Hình 3. Vị trí tương đối của hai đường thẳng 
 Ví dụ 3. Dùng GeoGebra mô phỏng phương trình đường tròn và đường thẳng trong 
bài học “Phương trình đường tròn” (SGK Hình học 10, tr. 83) (Tran et al., 2010). 
 Bài toán 3. (Tran et al., 2010) Viết phương trình Gợi ý: Đường tròn (C) có tâm I (1; 2 ) , sử 
 tiếp tuyến tại điểm M (3; 4) thuộc đường tròn dụng công thức (3), phương trình tiếp tuyến của 
 22
 (Cx ) : (− 1) +− ( y 2) = 8. đường tròn (C) tại điểm M (3; 4) là 
 xy+−=70 
 Sử dụng GeoGebra để mô phỏng Bài toán 3, ta có các bước dựng hình sau: 
 (1) Dựng đường tròn tâm I (1; 2 ) bán kính R = 22 theo phương trình 
 (xy− 1)22 +− ( 2) = 8 ; 
 (2) Lấy điểm M (3; 4) và tâm I (1; 2 ) ; 
 (3) Vẽ đoạn thẳng IM; 
 (4) Xác định đường thẳng qua M vuông góc với IM (đường thẳng này là tiếp tuyến với đường 
 tròn (C) tại điểm M). 
 Chiếu quá trình dựng hình và kết quả trên màn hình máy chiếu để HS xem và đối chiếu 
với kết quả tính toán thông qua lí thuyết vừa học (Hình 4). Chúng ta thấy rằng, phương trình 
đường thẳng tiếp tuyến của tính toán qua lí thuyết và của phần mềm GeoGebra là như nhau. 
 823 
Tạp chí Khoa học Trường ĐHSP TPHCM Tập 18, Số 5 (2021): 817-826 
 Hình 4. Vẽ tiếp tuyến đường tròn 
 Nhận xét chung: trong quá trình sử dụng phần mềm GeoGebra, khi thay đổi các tham 
số thì các thông số khác thay đổi theo, điều này phù hợp với thi trắc nghiệm đối với những 
bài có dạng tương tự. Mặt khác, HS cũng có thể sử dụng phần mềm trực tiếp trên trang web 
để tự so sánh kết quả tính toán khi làm bài tập ở nhà. 
4. Kết luận 
 Việc củng cố lí thuyết bài học Hình học thông qua các bài toán dưới sự mô phỏng bằng 
phần mềm GeoGebra đã góp phần sống động và thực tế hơn. Qua đó, HS nắm bắt, khắc sâu 
lí thuyết vừa học. Thật vậy, trong quá trình giảng dạy thực tế ở khối 10 tại Trường THPT 
Thực hành Cao Nguyên, tỉnh Đắk Lắk. Kết quả bước đầu thu được rất khả quan cho thấy, sự 
hiệu quả của việc sử dụng phần mềm GeoGebra trong khoảng thời gian củng cố lí thuyết bài 
học Hình học. Qua đó, chúng tôi cũng thấy rằng cần có sự linh hoạt trong việc áp dụng phần 
mềm GeoGebra với mỗi bài học, bài toán để việc củng cố bài học được hợp lí, tối ưu. Tiếp 
đó, chúng tôi sẽ nghiên cứu, hướng dẫn các giáo viên dạy Toán trong tổ bộ môn cùng ứng 
dụng phần mềm GeoGebra để mô phỏng, củng cố lí thuyết bài học Hình học của các lớp 11 
và 12. 
  Tuyên bố về quyền lợi: Tác giả xác nhận hoàn toàn không có xung đột về quyền lợi. 
  Lời cảm ơn: Cảm ơn TS Lê Anh Nhật Trường Đại học Tân Trào đã có những hướng dẫn, 
 góp ý tích cực trong thời gian giảng dạy thực tế và chuẩn bị bài báo này. 
 824 
Tạp chí Khoa học Trường ĐHSP TPHCM Vũ Thị Phương 
 TÀI LIỆU THAM KHẢO 
Dockendor, M., & Solar, H. (2017). ICT integration in mathematics initial teacher training and its 
 impact on visualization: the case of GeoGebra. Int. J. Math. Educ. Sci. Technol, 49(1), 66-84. 
Luong, V. H. (2018). Day hoc Toan theo dinh huong phat trien tu duy do thi duoi su ho tro cua phan 
 mem GeoGebra [Teaching Mathematics following the approach of developing graph thinking 
 with the help of Geogebra software]. Ho Chi Minh City University of Education, 15(10), 
 159-168. 
Nguyen, D. N., & Luckxay, P. (2015). Su dung phan mem GeoGebra ho tro day hoc Toan tai cac 
 truong trung hoc nuoc CHDCND Lao [Using GeoGebra software to supports teaching 
 mathematic at the secondary schools in Lao PDR]. Journal of Educational Equipment, 4, 
 81-83. 
Nguyen, P. L., & Le, T. P. (2015). Teaching parabola with dynamic software "GeoGebra": A 
 pedagogical experiment in Vietnam. Int. J. Educ. Res., 3(4), 423-436. 
Nguyen, M. H. & Huynh, T. L. (2018). Minh hoa day hoc chu de khoi da dien voi su ho tro cua phan 
 mem Geogebra [The illustration teaches polyhedron subjects with the support of GeoGebra 
 software]. Ho Chi Minh City University of Education, 15(4), 51-64. 
Nguyen, P. L., Le, V. M. T., & Nguyen, T. T. (2020). Status of using it in teaching: opinions of 
 mathematics teachers of Hau Giang province, Vietnam. European J. of Education Studies, 
 7(1), 42-51. 
Phan, T. H. (2013). Su dung phan mem Geogebra ho tro day hoc kham pha dinh ly [Using GeoGebra 
 software support for discovery learning theorems]. Can Tho University Journal of Science, 27, 
 61-66. 
Smirnov, V. A., & Smirnova, I. M. (2017). How to study the theory of geometry more effectively. 
 Mathematics at school, 2017(3), 34-39. 
Tang, M. D. (2020). Engaging pre-service mathematics teacher in using augmented reality 
 technology: the case of “3D calculator” app. Ho Chi Minh City University of Education, 17(3), 
 486-499. 
Tran, V. H., Nguyen, M. H., & Nguyen, V. D., & Tran, D. H. (2010). Hinh hoc 10 [Geometry 10]. 
 Hanoi: Vietnam Education Publishing House. 
Tran, T., Nguyen, T. T. T., & Dang, T. H. (2012). Su dung phan mem "Geogebra" lam phuong tien 
 truc quan trong day hoc gia bai tap phep bien hinh [Using the software geogebra as a means 
 of visual learning in teaching how to solve transformation problems]. UED J. of Social 
 Sciences, Humanities and Education, 2(1), 39-45. 
Tran, P. H. (2016). Phan mem GeoGebra 5.0: Huong dan su dung va ung dung trong mon toan cap 
 ba [GeoGebra Software: Instructions for use and Applications in High School Mathematics]. 
 Dong Nai, Vietnam. 
Vo, V. N., Vo, V. H., & Dang, V. Q. T.,... Tang, M. D.. (2020). Building an inventory of learning 
 materials exploiting mobile augmented reality technology for Spatial Geometry. Ho Chi Minh 
 City University of Education, 17(11), 1934-1944. 
 825 
Tạp chí Khoa học Trường ĐHSP TPHCM Tập 18, Số 5 (2021): 817-826 
 USING GEOGEBRA TO CONSOLIDATE GEOMETRY THEORY 
 Vu Thi Phuong 
 Cao Nguyen Practical High school, Tay Nguyen University, Vietnam 
 Corresponding author: Vu Thi Phuong – Email: phuongcaonguyen06@gmail.com 
 Received: February 17, 2021; Revised: April 27, 2021; Accepted: May 03, 2021 
ABSTRACT 
 Students learning geometry are usually required high levels of visual thinking and 
imagination. In order to help students with such visual thinking, we have examined the possibilities 
of applying GeoGebra software to teach geometry to reinforce the theory of each lesson. This article 
presents arguments and procedures for applying GeoGebra software for practices. Then, we apply 
the procedures to teach students in grades 10. In this paper, some examples will be presented. It is 
suggested to further study the use of GeoGebra software in teaching geometry with grades 11 
and 12. 
 Keywords: circle; equation; GeoGebra; geometry; high school; information technology; 
mathematics; simulation; teaching methods; teaching models 
 826