Quintic B-Spline collocation method for numerical solution a modified GRLW equations

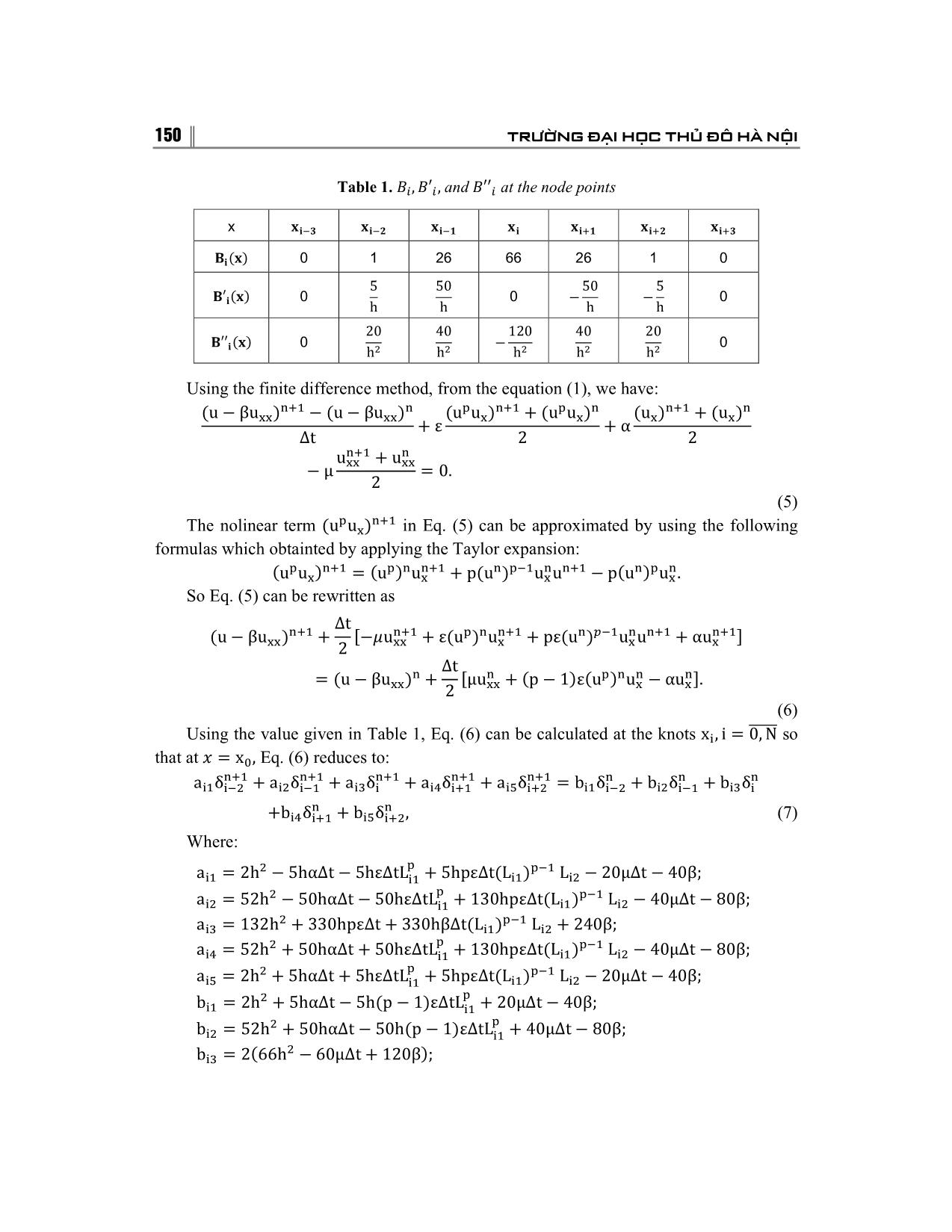
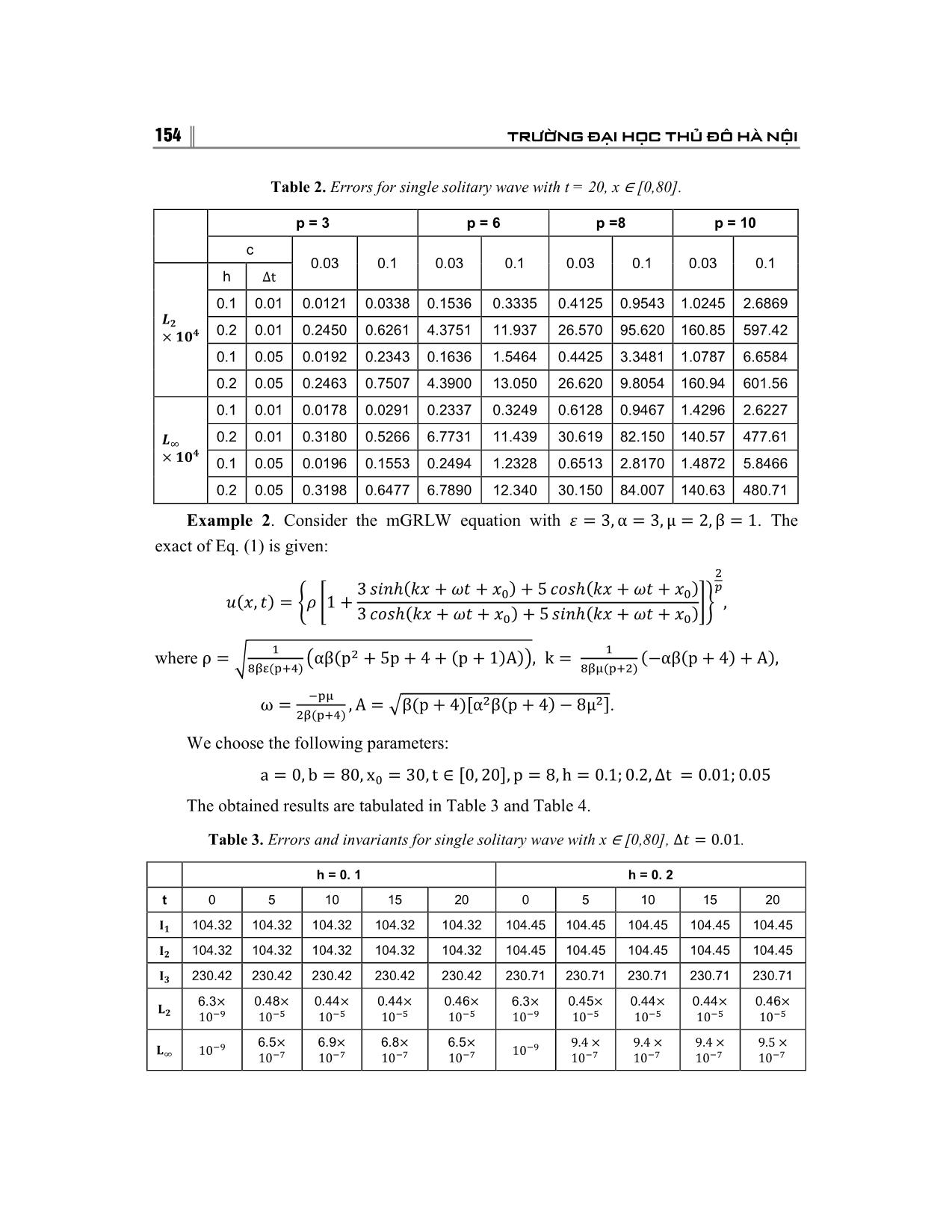
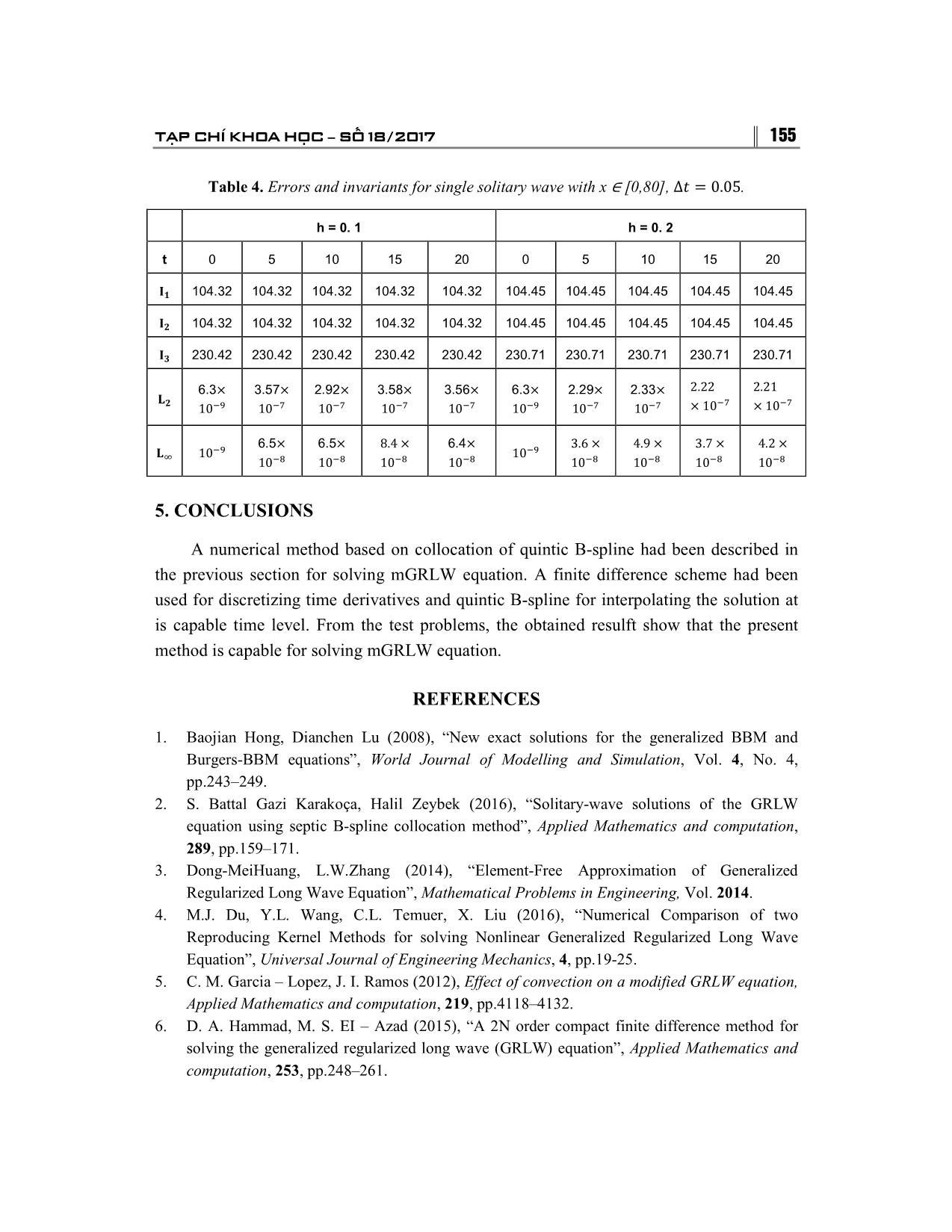
SPLINESPLINE COLLOCATION METHOD FOR NUMERICAL 
 SOLUTION A MODIMODIFIEDFIED GRLW EQUATIONS 
 Nguyen Van Tuan 
 Hanoi Metropolitan University 
 AbstractAbstract: In this paper, numerical solution of a modified generalized regularized long 
 wave (mGRLW) equation are obtained by a method based on collocation of quintic B – 
 splines. Applying the von – Neumann stability analysis, the proposed method is shown to 
 be unconditionally stable. The numerical result shows that the present method is a 
 successful numerical technique for solving the GRLW and mRGLW equations that they 
 have real exact solutions. 
 KeywordsKeywords: mGRLW equation; quintic Bspline; collocation method; finite difference. 
 Email: nvtuan@daihocthudo.edu.vn 
 Received 12 July 2017 
 Accepted for publication 10 September 2017 
1. INTRODUCTION 
 In this paper we consider the solution of the mGRLW equation: 
 (1) 
 
 u  αu  εu u  μu  βu  0,
with the initial xcondition: ∈ a, b, t ∈ 0, T,
 (2) 
and the boundaryu x,condition: 0  fx , x ∈ a, b,
 ua, t  0, ub, t  0 (3) 
  ua, t  ua, t  0
 u a, t  u b, t  0,
where are constants, is an integer. 
 Theα, ε,mGRLW μ, β, p (1) is called theμ  generalized 0, β  0, p regularized long wave (GRLW) equation if 
 the generalized equal width (GEW) equation if the regularized long 
waveμ  0, (RLW) equation or Benjamin – Bona – Mohonyα  0, (BB μ M) 0, equation if 
 etc. β  1, 
p  1, 
TẠP CHÍ KHOA HỌC −−− SỐ 18/2017 149 
 Equation (1) describes the mathematical model of wave formation and propagation in 
fluid dynamics, turbulence, acoustics, plasma dynamics, ect. So in recent years, researchers 
solve the GRLW and mGRLW equation by both analytic and numerical methods. The 
GRLW equation is solved by finite difference method [6], Petrov – Galerkin method [8], 
distributed approximating functional method [7], IMLS – Ritz method [3], methods use the 
B – spline as the basis functions [2], exact solution methods [9]. The mGRLW is solved by 
reproducing kernel method [4], time – linearrization method [5], exact solution method [1]. 
 In this present paper, we have applied the pentic B – spline collocation method to the 
GRLW and mGRLW equations. This work is built as follow: in Section 2, numerical 
scheme is presented. The stability analysis of the method is established in Section 3. The 
numerical results are discussed in Section 4. In the last Section, Section 5, conclusion is 
presented. 
2. QUINTIC B – SPLINE COLLOCATION METHOD 
 The interval is partitioned in to a mesh of uniform length by the 
knots such,  that: h  x  x
 x, i  0, N 
 Our numerical study fora mGRLW x  x equation ⋯  x using  the x collocation b. method with quintic 
Bspline is to find an approximate solution to exact solution in the form: 
 Ux, t ux, t (4) 
 
 are theU x,quintic t  ∑ Bspline δ tbasisBx functions, at knots, given by [4]. 
 Bx
 
 x  x , x  x  x
   
 x  x  6x  x , x  x  x
    
  x  x  6x  x  15 x  x , x  x  x
   
  x  x  6x  x  15 x  x  
   
 1 20 x  x , x  x  x
 Bx      
 h x  x  6x  x  15 x  x  20 x  x 
 
  15 x  x , x  x  x
     
 x  x  6x  x  15 x  x  20 x  x 
   
  15 x  x  6x  x , x  x  x
 The value of  and its derivatives0, x may be tabulated  x as∪ in x Table x 1. . 
 Bx
 U  δ  26δ  66δ  26δ  δ 
 5
 U′   δ  10δ  10δ  δ
 h 
 20
 U′′    δ  2δ  6δ  2δ  δ.
 h
150 TRƯỜNG ĐẠI HỌC THỦ ĐÔ H NỘI 
 Table 1. and at the node points 
 , ′, ′′ 
 x 
       
 0 1 26 66 26 1 0 
 
 0 0 0 
 5 50 50 5
 ′  
 h h h h
 0 0 
 20 40 120 40 20
 ′′       
 h h h h h
 Using the finite difference method, from the equation (1), we have: 
        
 u  βu   u  βu  u u  u u u  u
  ε  α
 Δt 2 2
   
 u  u
  μ  0.
 2 (5) 
  
 The nolinear term u u in Eq. (5) can be approximated by using the following 
formulas which obtainted by applying the Taylor expansion: 
            
 u u  u  u  pu  u u  pu  u . 
 So Eq. (5) can be rewritten as 
 Δt
 u  βu   u  εuu  pεuuu  αu
  2    
 Δt
  u  βu   μu  p  1εuu  αu. 
  2   
 (6) 
 Using the value given in Table 1, Eq. (6) can be calculated at the knots x, i  0, N so 
that at   x, Eq. (6) reduces to: 
        
 a δ  a δ  a δ  a δ  a δ  b δ  b δ  b δ 
  
 b δ  b δ, (7) 
 Where: 
   
 a  2h  5hαΔt  5hεΔtL  5hpεΔtL  L  20μΔt  40β; 
   
 a  52h  50hαΔt  50hεΔtL  130hpεΔtL  L  40μΔt  80β; 
  
 a  132h  330hpεΔt  330hβΔtL  L  240β; 
   
 a  52h  50hαΔt  50hεΔtL  130hpεΔtL  L  40μΔt  80β; 
   
 a  2h  5hαΔt  5hεΔtL  5hpεΔtL  L  20μΔt  40β; 
  
 b  2h  5hαΔt  5hp  1εΔtL  20μΔt  40β; 
  
 b  52h  50hαΔt  50hp  1εΔtL  40μΔt  80β; 
 
 b  266h  60μΔt  120β ; 
TẠP CHÍ KHOA HỌC −−− SỐ 18/2017 151 
  
 b  52h  50hαΔt  50hp  1εΔtL  40μΔt  80β; 
  
 b  2h  5hαΔt  5hp  1εΔtL  20μΔt  40β;
 L  δ  26δ  66δ  26δ  δ
 TheL  system δ  (7) 10δ  consists 10δ  of δ. equations in the knowns 
 N  1 N  5
 
δTo, δ get,  a ,solution δ, δ to this. system, we need four additional constraints. These constraints 
are obtained from the boundary conditions (3) and can be used to eliminate from the 
system (7). Then, we get the matrix system equation 
 (8) 
    
 Aδwhereδ the matrix Bδ δ  r, are pentadiagonal matrices and is 
  
the dimensionalAδ colum, Bδ vector. The algorithm is Nthen 1 us ed N to solve 1 the system (8).r 
We Napply  1 first the intial condition: 
 (9) 
  
then we need that the approximatelyUx, 0  ∑ solutionδ Bx is, satisfied folowing conditions: 
 Ux, 0  fx
 
 Ux, 0  Ua, 0  0
  (10) 
 Ux, 0  Ub, 0  0
 U x, 0  U a, 0  0
 U x, 0  U b, 0  0
 Eliminating  iand  0,1,  from , N. the system (11), we get: 
    
 δ, δ, δ δ 
 
where is the pentadiagonal matrix givenAδ by: r,
 A
  54 60 6 0 0 0 ... 0 
  
 101 135 105
  1 0 0 ... 0 
  4 2 4 
  1 26 66 26 1 0 ... 0 
  
  ... ... ... 
 A =
  ... ... ... 
  
  0 ... 0 1 26 66 26 1 
  
 105 135 101
  0 ... 0 0 1 
  4 2 4 
  
  0 ... 0 0 0 6 60 54 
and 
      
 δ  δ, δ,  , δ , r  fx, fx,  , fx .
152 TRƯỜNG ĐẠI HỌC THỦ ĐÔ H NỘI 
3. STABILITY ANALYSIS 
 To apply the VonNeumann stability for the system (6), we must first linearize this 
system. 
 We have: 
 (11) 
  
 δ  ξ exp iγjh  , i  1,
where is the mode number and is the element√ size. 
 Beingγ applicable to only linearh schemes the nonlinear term is linearized by 
 
taking as a locally constant value The linearized form of proposedU Uscheme is given as: 
 U k.
       
 pδ  pδ  pδ  p δ  pδ  p′ δ  p′ δ  (12) 
   
 Where:p′ δ   p′ δ  p′ δ 
  
 p  1  M  N  P 
  
 p  26  10M  2N  2P
  
 p  66  6N  6P 
  
 p  26  10M  2N  2P
  
 p  1  M  N  P 
  
 p′  1  M  N  P 
 p′   26  10M  2N   2P
  
 p′  66  6N  6P 
 p′   26  10M  2N  2P
 p′   1  M  N  P,
  
 5α  εk ∆t
 M  , 
 h
 10μ∆t 10β
 N   , P   .
 Substitretion of h h into Eq. (12) leads to: 
  
 δ  exp iγjh ξ , 
 ξp exp 2ihγ  p exp iγh  p  p exp iγh  p exp 2iγh  (13) 
 Simplifyingp′  exp 2iγh Eq. (13), p′ we get:exp iγh  p′   p′  exp iγh  p′  exp 2iγh.
 A  iB
  
 C  iB
TẠP CHÍ KHOA HỌC −−− SỐ 18/2017 153 
 Where: 
       
 A  2 1  N  P cos 2ϕ  4 13  N  P cosϕ  66  6N  6P;
  
 B  2M sin 2ϕ  10 ; 
       
 C  2 1  N  P cos 2ϕ  4 13  N  P cosϕ  66  6N  6P;
 It α,γ is clear 0,ϕ that γh. 
  
 Therefore, theC  linearized A . numerical scheme for the mGRLW equation is 
unconditionally stable. 
4. NUMERICAL EXAMPLE 
 We now obtain the numerical solution of the GBBMB equation for a problem. To 
show the efficiency of the present method for our problem in comparison with the exact 
solution, we report and using formula: 
 L L 
 L  max |Ux, t  ux, t|,
 
  
 
 L  h |Ux, t  ux, t|  ,
 
where is numerical solution and denotes exact solution. 
 ThreeU invariants of motion whichu correspond to the conservation of mass, momentum, 
and energy are given as 
   
  
 I   udx, I   u  βudx, 
  
  
  2βp  1 
 I   u  u dx.
 
 Example 1 . Consider the GRLW equation withε . The exact of 
Eq. (1) is given in [7] 3,αμ0,β1
  
  1 2  
 ux, t   sech  x  x  ct.
 2 2
 We choose the following parameters 
 
 Thea0; b obtained 80; x results are 30; Ttabulated  20;p in Table  3;6;8;10;c 2.  0.03;0.01;h  0.1;0.2
154 TRƯỜNG ĐẠI HỌC THỦ ĐÔ H NỘI 
 Table 2. Errors for single solitary wave with t = 20, x ∈ [0,80]. 
 p = 3 p = 6 p =8 p = 10 
 c 
 0.03 0.1 0.03 0.1 0.03 0.1 0.03 0.1 
 h 
 0.1 0.01∆t 0.0121 0.0338 0.1536 0.3335 0.4125 0.9543 1.0245 2.6869 
 0.2 0.01 0.2450 0.6261 4.3751 11.937 26.570 95.620 160.85 597.42 
  
 
   0.1 0.05 0.0192 0.2343 0.1636 1.5464 0.4425 3.3481 1.0787 6.6584 
 0.2 0.05 0.2463 0.7507 4.3900 13.050 26.620 9.8054 160.94 601.56 
 0.1 0.01 0.0178 0.0291 0.2337 0.3249 0.6128 0.9467 1.4296 2.6227 
 0.2 0.01 0.3180 0.5266 6.7731 11.439 30.619 82.150 140.57 477.61 
  
  0.1 0.05 0.0196 0.1553 0.2494 1.2328 0.6513 2.8170 1.4872 5.8466 
  
 0.2 0.05 0.3198 0.6477 6.7890 12.340 30.150 84.007 140.63 480.71 
 Example 2 . Consider the mGRLW equation with . The 
exact of Eq. (1) is given: 3,α3,μ2,β1
 
  
 3       5     
 ,    1   ,
 3       5     
where 
   
 ρ   αβ p  5p  4  p  1A, k   αβ p  4  A,
 . 
   
 ω   , A  βp  4α βp  4  8μ 
 We choose the following parameters: 
 
 The obtaineda  results 0, b  are 80, tabulated x  30, in t ∈Table0, 20 3 and,p Table 8,h 4. 0.1;0.2,∆t  0.01;0.05
 Table 3. Errors and invariants for single solitary wave with x [0,80], . 
 ∈ ∆  0.01
 h = 0. 1 h = 0. 2 
 t 0 5 10 15 20 0 5 10 15 20 
 104.32 104.32 104.32 104.32 104.32 104.45 104.45 104.45 104.45 104.45 

 104.32 104.32 104.32 104.32 104.32 104.45 104.45 104.45 104.45 104.45 

 230.42 230.42 230.42 230.42 230.42 230.71 230.71 230.71 230.71 230.71 

 6.3 0.48 0.44 0.44 0.46 6.3 0.45 0.44 0.44 0.46
           
          
 10 10 10 10 10 10 10 10 10 10
 6.5 6.9  6.8  6.5   9.4  9.4  9.4  9.5  
     10    
  10  10 10 10 10 10 10 10 
 10
TẠP CHÍ KHOA HỌC −−− SỐ 18/2017 155 
 Table 4. Errors and invariants for single solitary wave with x ∈ [0,80], ∆  0.05 . 
 h = 0. 1 h = 0. 2 
 t 0 5 10 15 20 0 5 10 15 20 
 104.32 104.32 104.32 104.32 104.32 104.45 104.45 104.45 104.45 104.45 

 104.32 104.32 104.32 104.32 104.32 104.45 104.45 104.45 104.45 104.45 

 230.42 230.42 230.42 230.42 230.42 230.71 230.71 230.71 230.71 230.71 

 6.3 3.57 2.92 3.58 3.56 6.3 2.29 2.33
         2.22  2.21  
          
 10 10 10 10 10 10 10 10  10  10
 6.5 6.5  8.4  6.4  3.6  4.9  3.7  4.2  
  10  
  10  10  10  10  10  10  10  10  
  10
5. CONCLUSIONS 
 A numerical method based on collocation of quintic Bspline had been described in 
the previous section for solving mGRLW equation. A finite difference scheme had been 
used for discretizing time derivatives and quintic Bspline for interpolating the solution at 
is capable time level. From the test problems, the obtained resulft show that the present 
method is capable for solving mGRLW equation. 
 REFERENCES 
1. Baojian Hong, Dianchen Lu (2008), “New exact solutions for the generalized BBM and 
 BurgersBBM equations”, World Journal of Modelling and Simulation , Vol. 4, No. 4, 
 pp.243–249. 
2. S. Battal Gazi Karakoça, Halil Zeybek (2016), “Solitarywave solutions of the GRLW 
 equation using septic Bspline collocation method”, Applied Mathematics and computation , 
 289 , pp.159–171. 
3. DongMeiHuang, L.W.Zhang (2014), “ElementFree Approximation of Generalized 
 Regularized Long Wave Equation”, Mathematical Problems in Engineering, Vol. 2014 . 
4. M.J. Du, Y.L. Wang, C.L. Temuer, X. Liu (2016), “Numerical Comparison of two 
 Reproducing Kernel Methods for solving Nonlinear Generalized Regularized Long Wave 
 Equation”, Universal Journal of Engineering Mechanics , 4, pp.1925. 
5. C. M. Garcia – Lopez, J. I. Ramos (2012), Effect of convection on a modified GRLW equation, 
 Applied Mathematics and computation , 219 , pp.4118–4132. 
6. D. A. Hammad, M. S. EI – Azad (2015), “A 2N order compact finite difference method for 
 solving the generalized regularized long wave (GRLW) equation”, Applied Mathematics and 
 computation , 253 , pp.248–261. 
156 TRƯỜNG ĐẠI HỌC THỦ ĐÔ H NỘI 
7. E. Pindza, E. Mare (2014), “Solving the generalized regularized long wave equation using a 
 distributed approximating functional method”, International J. Computational Mathematics, 
 Vol. 2014 . 
8. Thoudam Roshan (2012), “A Petrov – Galerkin method for solving the generalized regularized 
 long wave (GRLW) equation”, Computers and Mathematics with applications , 63 , pp.943956. 
9. Wang JuFeng, Bai FuNong and Cheng YuMin (2011), “A meshless method for the 
 nonlinear generalized regularized long wave equation”, Chin. Phys. B Vol. 20 , No. 3, 
 p.030206. 
 PHƯƠNG PHÁP COLLOCATION VI CƠ S BSPLINE BC 5 
 GII PHƯƠNG TRÌNH GENERALIZED BENJAMINBONA
 MAHONYBURGERS 
 Tóm tttttt: Trong bài báo này chúng ta s dng phương pháp collocation vi cơ s B – 
 spline bc 5 gii xp x phương trình mGRLW. S dng phương pháp Von – Neumann h 
 phương trình sai phân n ñnh vô ñiu kin. Kt qu s chng t phương pháp ñưa ra 
 hu hiu ñ gii phương trình trên. 
 TTTT khóakhóa: Phương trình mGRLW, spline bc 5, phương pháp collocation, phương pháp 
 sai phân hu hn.