Predicting the bearing capacity of pile installed into cohesive soil concerning the spatial variability of SPT data (A case study)
Nowadays, in situ tests have played a viable role in
geotechnical engineering and construction technology. Besides lab
tests conducted on undisturbed soil samples, many different kinds of
in-situ tests were used and proved to be more efficient in foundation
design such as pressuremeter PMT, cone penetration test CPT,
standard SPT, etc. Among them, a standard penetration test (SPT for
short) is easy to carry out at the site. For decades, it has proved
reliable to sandy soil, but many viewpoints and opinions argued that
the test was not appropriately applicable to cohesive soil because of
scattered and dispersed data of SPT blow counts through different
layers. This paper firstly studies how reliable the SPT data can
predict the physical and mechanical properties; secondly, the soil
strength is determined in terms of corrected N-SPT values, and
finally the bearing capacity of a pile penetrating cohesion soil. By
analyzing data from 40 boreholes located in 18 projects in Ho Chi
Minh City, South VietNam, coefficients of determination between
SPT numbers and physical and mechanical properties of different
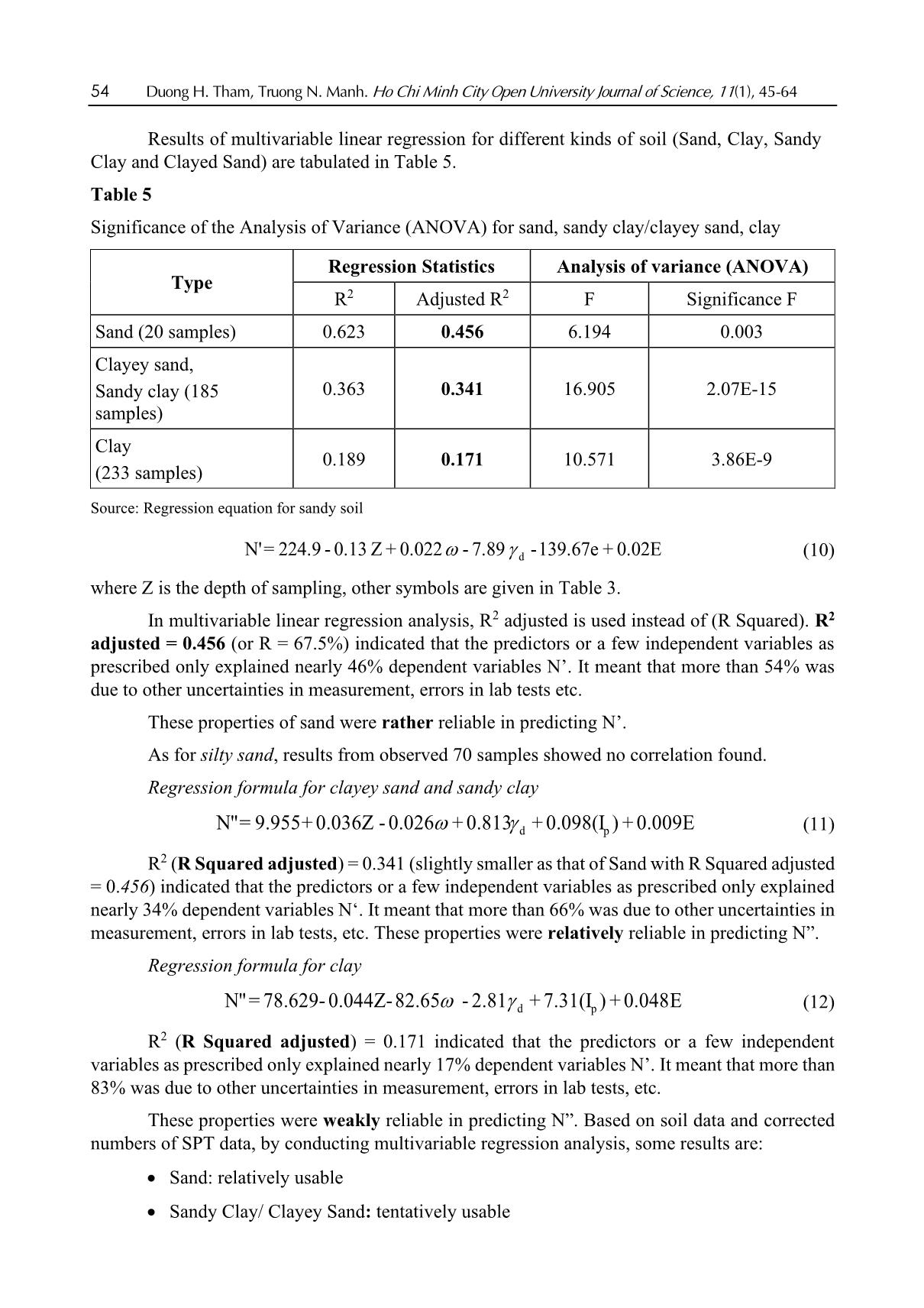
soil kinds are not the same: R2 = 0.623 for sand, =0.363 for sandy
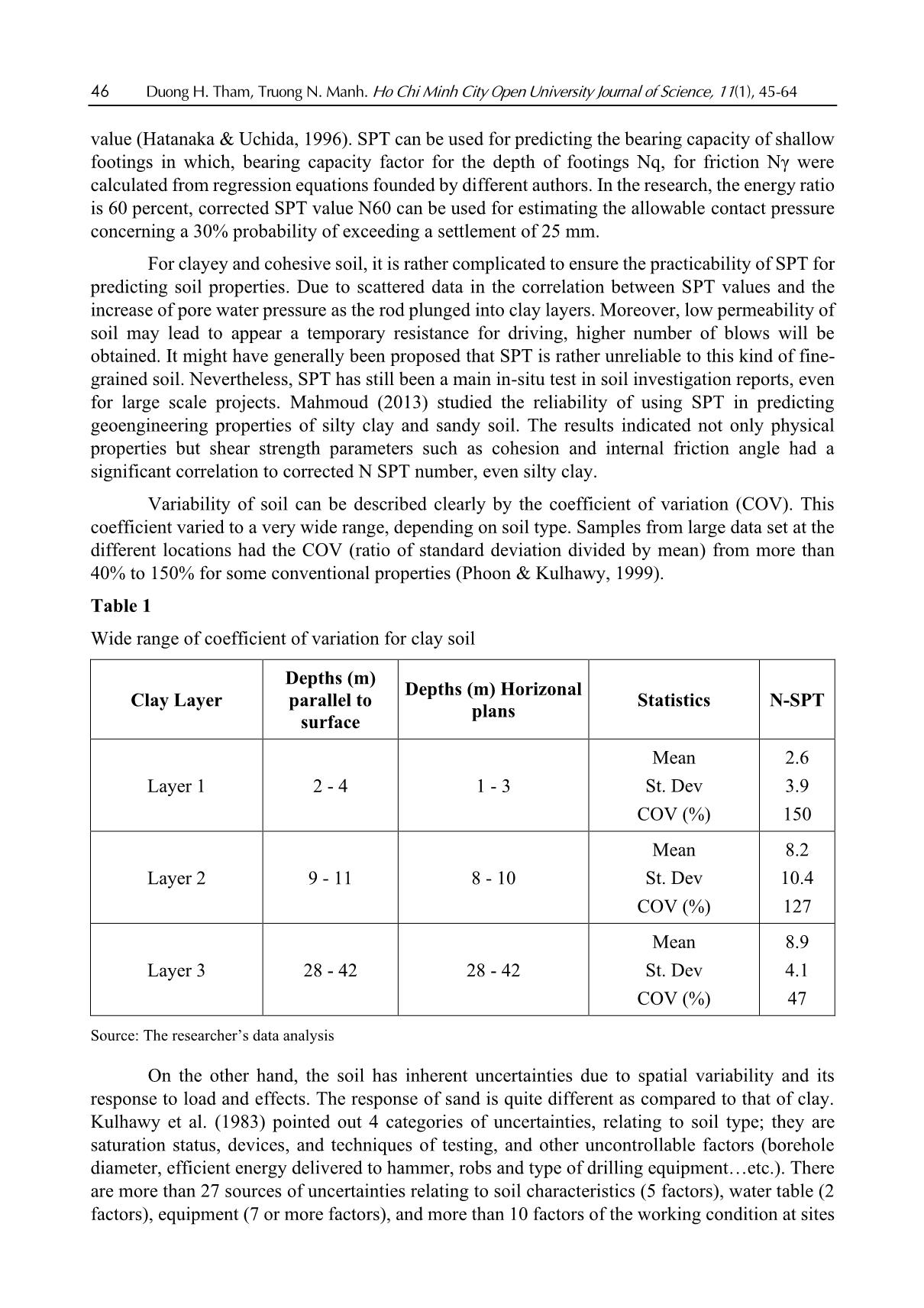
clay and =0.189 for clay. The spatial variability of soil properties is
taken into account by calculating the scale of fluctuation θ=4.65m
beside the statistically-based data in horizontal directions. Finally,
the results from two theoretical approaches of predicting pile bearing
capacity were compared to those of finite element program Plaxis
3D and static load test at site. Correlation between the capacity
computed by using corrected N-values instead of soil strength and
results of static load test has proved to be well suitable in evaluating
the bearing capacity of driven and jack-in piles, particularly
installing in the cohesive soil using the SPT blows.

Trang 1
Trang 2

Trang 3

Trang 4
Trang 5

Trang 6
Trang 7

Trang 8

Trang 9
Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Predicting the bearing capacity of pile installed into cohesive soil concerning the spatial variability of SPT data (A case study)

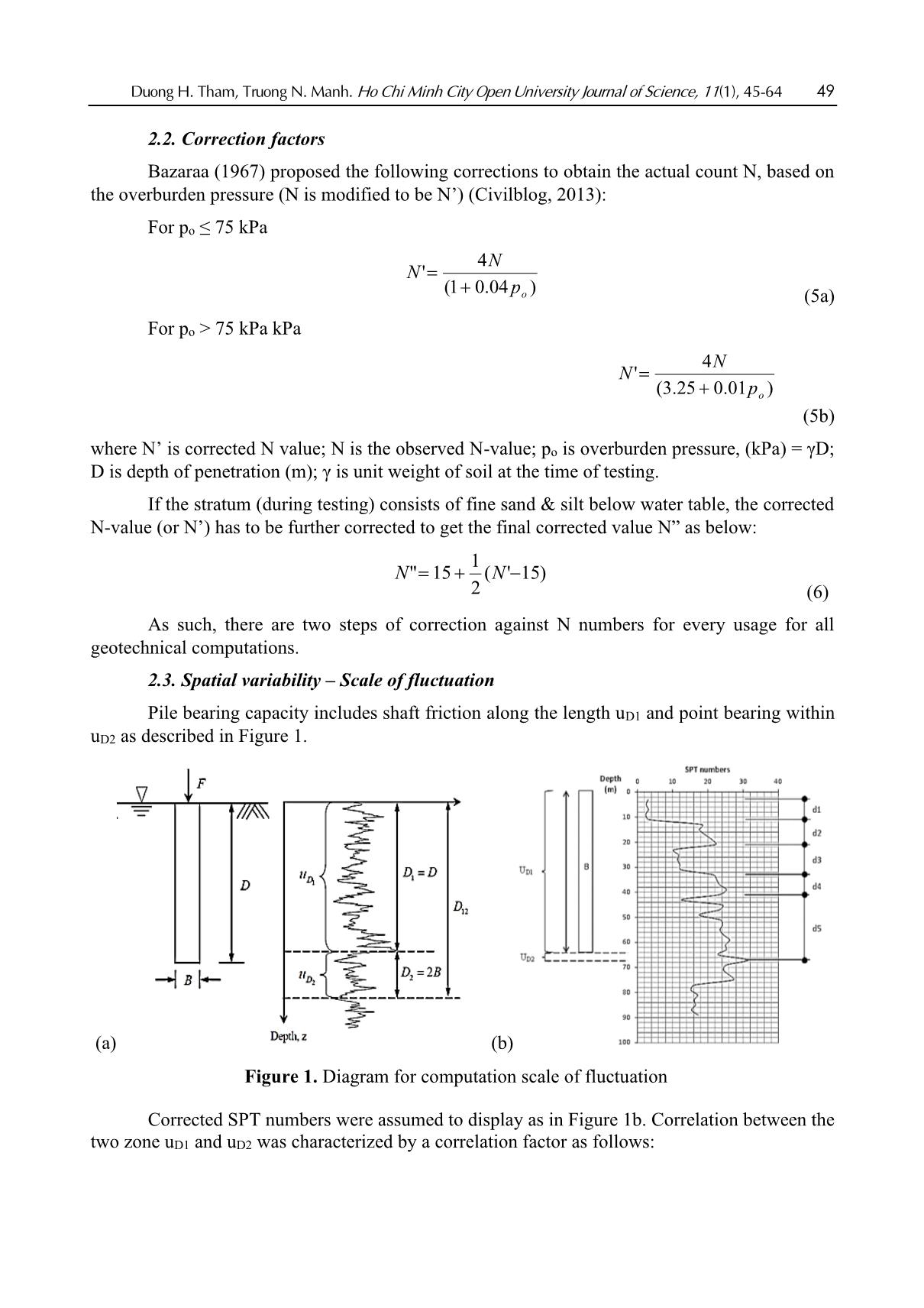
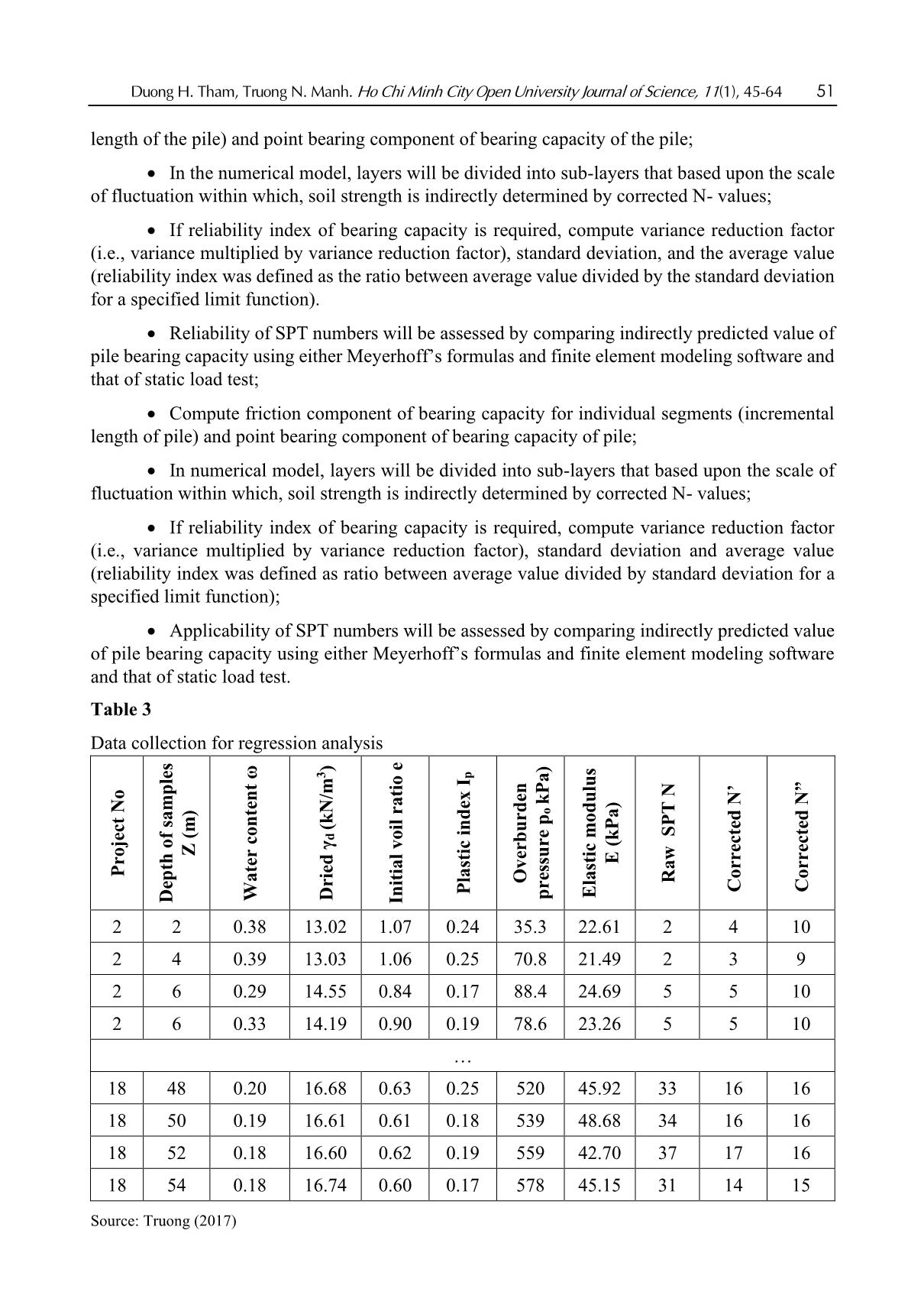
No. Soil layers γ Ϭ’ ϕ c a Cu,i k fi Axq Qsi ness vo SPT p 2 m kN/m3 kN/m2 (o) kPa kPa kN/m2 m2 (kN) Firmly 1 plastic clay 2 19.8 19.8 16.8 2.4 7.75 1 8.39 2 8.4 2.8 23.5 Firmly 2 plastic clay 2 19.8 59.4 16.8 2.4 13.9 1 20.31 2 20.3 2.8 56.9 Firmly 3 plastic clay 1.7 19.8 96.0 16.8 2.4 13.4 1 31.33 2 31.3 2.4 74.6 Granular 4 soil, dense 1.9 2.02 13.21 31.3 0 13.6 0.63 80.29 2 50.5 2.7 134.2 Plastic 4 clayey sand 0.8 1.05 15.54 25.2 1.1 12.9 0.68 74.24 2 50.2 1.1 56.2 Friction component (kN) 345.3 Np k1 qb Ab Qb Point bearing component kPa m2 kN 13.2 400 5260 0.12 644.4 644.4 Total bearing capacity (kN) 989.7 Source: Truong (2017) If the uncorrected N values are used, bearing capacity equals approximately to 85.86 tons with: • Friction component: 282.6 kN (-18.1% as compared to that of using corrected N); Duong H. Tham, Truong N. Manh. Ho Chi Minh City Open University Journal of Science, 11(1), 45-64 59 • Point bearing component: 572.8 kN (-11.1% as compared to that of using corrected N). 4.3. Bearing capacity suggested by Architectural Institute of Japan (item G.3.2 of the TCVN 10304: 2014) (Ministry of Sciences and Technology, Vietnamese Government, 2014) Appendix G of National Standard (TCVN 10304: 2014, Ministry of Sciences and Technology, Vietnamese Government, 2014) described steps to apply the main contents of Recommendations for Design of Building Foundation (Architectural Institute of Japan issued in 1988, hereinafter denoted AIJ for short) in predicting the bearing capacity of pile, both driven and bored piles. SPT data were used to indirectly compute friction fs,i and point bearing resistance qb th by formulas (15) and (17) where Ns.i is average number of SPT in the i soil layer; Np is average value of SPT blow counts taken within a zone 1D below the pile tip level and 4D above level of the pile tip. An Excel spreadsheet for computing bearing capacity was displayed as in Table 9 below: Table 9 Illustrated spreadsheet for computing abutment B pile bearing capacity using recommendation of AIJ and corrected N’, borehole BH-1 WITH CORRECTED N VALUES 8.4 m 8.4 BH-1 0.35 m (D=0.35m) No Soil layers thickness γ Ϭ’vo SPT aP fL Cu,i fi Axq Qsi m kN/m3 kN/m2 KPa kN/m2 m2 kN 1 Firmly plastic clay 2 19.8 19.8 7.8 0.5 1 48.44 24.2 2.8 67.8 2 Firmly plastic clay 2 19.8 59.4 14.0 0.5 1 87.29 43.6 2.8 122.2 3 Firmly plastic clay 1.7 19.8 96.03 13.4 0.5 1 83.99 42.0 2.38 100 Granular soil, 4 1.9 20.2 132.1 13.6 0.7 1 85.26 04.5 2.66 12.1 dense 5 Plastic clayey sand 0.8 10.5 155.4 13.0 0.8 1 81.21 65.6 1.12 73.5 Friction component (kN) 375.6 Np k1 qb Ab Qb Point bearing kPa m2 kN component 13.2 400 5260 0.12 88.2 88.2 Total bearing capacity (kN) 463.8 Source: Truong (2017) For uncorrected N blow counts, total bearing capacity equals approximately to 378 kN with: • Friction component: 305 kN (-18.8% as compared to that of using corrected N). • Point bearing component: 73 kN (-17.2% as compared to that of using corrected N). 4.4. Bearing capacity determined by numerical method For comparison purposes, a Plaxis 3D model was used in Figure 6. Mohr-Coulomb (MC) soil behavior model was chosen because of its relevancy to the bearing capacity problem, partly because of limited data from soil reports (without results from triaxial compression tests). Data of 60 Duong H. Tham, Truong N. Manh. Ho Chi Minh City Open University Journal of Science, 11(1), 45-64 soil properties input into software were converted from corrected SPT N-values, as abovementioned regression equations of Table 7. Calibration for the model was disregarded in case accepting a linear proportion factor between measured bearing capacity and computed one. Figure 6. Plaxis model for determining bearing capacity of pile At-site determination of the ultimate bearing capacity of a pile has complied with item 7.3.2 of TCVN 10304: 2014 (Ministry of Sciences and Technology, Vietnamese Government, 2014) “Pile Foundation - Code for design building foundation and construction works” that admitted a settlement at failure as below: S = .S gh (20) where, Sgh is settlement at ultimate condition, taken as 40mm (item 7.3.2); ξ = 0.2. As such, ultimate bearing capacity will be the load at which the pile settlement equals to 8 mm: Figure 7. Ultimate bearing capacity of 35cm square pile from static load test and Plaxis model (Truong, 2017) Ultimate bearing capacity by static load test is 676.8 kN, while this value is determined by yield point (big displacement at a constantly kept load) at P=473.7 kN (solid circle line in Figure 7). Three piles with different configuration were considered: For borehole BH1 with 5 layers: Duong H. Tham, Truong N. Manh. Ho Chi Minh City Open University Journal of Science, 11(1), 45-64 61 abutment B pile (square 35cm, L=8.4 m) and pile P58 (square 25cm pile, L=8.6 m). For borehole BH2, with 7 layers: pile P61 (square 30cm, L=12.2 m). Calculating spreadsheets are established as in Table 8, Table 9. Results are compared as shown in Figure 8: Figure 8. Comparisons between ultimate bearing capacity of pile using Meyerhoff’s formula, AIJ, Plaxis and Static Load Test (Truong, 2017) 4.5. Discussion • Correlation equations in Table 5 should be studied within the scale of fluctuation for higher R2 (adj.) instead of the entire soil profile. But since the thickness of soil layers was smaller than the scale of fluctuation θ, and R2 (adj.) was very high, therefore, the calculation for bearing capacity would be implemented with sufficient and reasonable accuracy in practice. By applying the scale of fluctuation, the spatial variability is taken into account, so the bearing capacity for the pile is calculated with a more rigorous procedure. • Regression equations for converting N-values into soil strength might have some errors. The most likely value may be computed by the square root of the sum of squares (or SRSS) law as follows: C = (C )2 + (C )2 + (C )2 design labtest convert mod el (21) in which, the first term belongs to soil properties obtained by conventional lab tests; the second term refers to measurement or correlation with corrected N-values, and the third term relates to formula of shaft friction and tip resistance (Cherubini & Vessia, 2010). • Back analysis to calibrate the numerical model is necessarily conducted for obtaining the proper set of soil strength properties unless a linear correlation in the elastic domain is found. • Load - displacement curve obtained by Plaxis indicated that soil foundation for the pile was still workable in the elastic domain. Meanwhile, results from the static load test showed a sharper trend in curvature, indicating a yielding point in the bearing capacity of the soil foundation. • Bearing capacity computed by AIJ using directly corrected N-values proved to be close to that of the static load test (Figure 8). Furthermore, comparison on results of bearing capacity obtained by two approaches, (one from numerical finite element model _ Plaxis 3D, using converting data of soil properties from N-values_, and the other from static load test) pointed out 62 Duong H. Tham, Truong N. Manh. Ho Chi Minh City Open University Journal of Science, 11(1), 45-64 that there was a linear correlation between them as in Figure 9 as following: Figure 9. Results of bearing capacity obtained by Plaxis, A.I.J v/s by Static Load Test This may come to a suggestion that corrected N-values can be used tentatively in predicting the bearing capacity of pile installing into cohesive soil at a specific site, and AIJ formula using directly corrected N-values will be more predictable than other analytical approaches. Single variable linear regression analysis at a level of confidence of 95% provides a set of converted parameters of soil strength_friction angle and cohesion_ which is possible to predict bearing capacity in a numerical model. 4. Conclusion The bearing capacity of a pile installing into cohesion soil can be assessed by comparing the results obtained by theoretical formulas using converting corrected N-values, numerical model, and static load tests. Multivariable linear regression analysis showed a weak correlation between N-values and physical properties of the cohesive soil and depth of testing, but single variable linear regression model showed a significant correlation of corrected N values to cohesive soil strength (i.e., friction angle and cohesion) with a level of confidence 95%. The spatial variability is taken into account with the scale of fluctuation, θ, postulated by Vanmarcke (1977). The soil profile characterized by the numbers of SPT blows is divided into segments of which its length is smaller than θ. Two locally used approaches including the Meyerhoff’s formula, and recommendation suggested by the Architectural Institute of Japan, Appendix G, item G.3.2 (TCVN 10304: 2014, Ministry of Sciences and Technology, Vietnamese Government, 2014) were used in which the soil strength were indirectly converted from corrected N-values and assigned as input data into models; the results were compared to those of numerical model Plaxis 3D and static load test. Results indicated that the approach of AIJ using directly SPT data predicted a closer value of bearing capacity as compared to that of the static load test. Besides, the numerical model Plaxis 3D using indirect SPT data (i.e., model converted SPT data to soil strength and compressibility) pointed out a value of bearing capacity which was a highly linear correlation to the reliable result of the static load test. These results could help practitioners in estimating bearing capacity with SPT data with a satisfactory accuracy. References Aoki, N., & Velloso, D. A. (1975). An approximate method to estimate the bearing capacity of piles. Proceedings of the Fifth Pan-American conference on soil mechanics and foundation engineering (pp. 367-376). Buenos Aires, Argentina: Sociedad Argentina de Mecanica de suelos e Ingenieria de Fundaciones. Duong H. Tham, Truong N. Manh. Ho Chi Minh City Open University Journal of Science, 11(1), 45-64 63 Bazaraa, A. R., & Kurkur, M. M. (1986). N-Values used to predict settlements of piles in Egypt. Proccedings of in situ tests in Geotechnical engineering (pp. 462-474). New York, NY: American Society of Civil Engineers. Cherubini, C., & Vessia, G. (2010). Reliability based pile design in sandy soils by CPT measurements. Georisk: Assessment and Management of Risk for Engineered Systems and Geo-Hazards, 4(1), 2-12. doi:10/1080/17499510902798156 Civilblog. (2013). Correction applied to SPT value. Retrieved January 20, 2021, from https://civilblog.org/2013/05/13/correction-applied-to-spt-value Duong, T. T. (2017). Estimating allowable bearing capacity of bored pile using Plaxis incorporated with theory of FORM reliability (Unpublished master’s thesis). Ho Chi Minh City Open University, Ho Chi Minh, Vietnam. Hatanaka, M., & Uchida, A. (1996). Empirical correlation between penetration resistance and internal friction angle of sandy soils. Soils and Foundations, Japanese Geotechnical Society, 36(4), 1-9. Hoang, T. Q., & Tam, N. M. (2016). Predicting bearing capacity of pile from N-SPT and method of numerical model (Unpublished master’s thesis). University of Technology, Vietnam National University, Ho Chi Minh, Vietnam. Honjo, Y. (2011). Challenges in geotechnical reliability based design. Retrieved December 15, 2020, from https://henry.baw.de/bitstream/20.500.11970/99549/1/1_02.pdf Kudmetha, K. K., & Dey, A. (January, 2012). Uncertainty in predicting bearing capacity of piles in sand using SPT data. Paper presented at the International symposium on engineering under uncertainty: Safety assessment and management (ISEUSAM), Howrah, India. Kulhawy, F. H., & Mayne, P. W. (1990). Manual on estimating soil properties for foundation design. Palo Alto, California: Electric Power Research Institute. Kulhawy, F. H., Traumann, C. H., Beech, J. F., O’Rourke, T. D., McGuire, W., Wood W. A., & Capano, C. (1983). Transmission line structure foundations for uplift-compression loading. Palo Alto, California: Electric Power Research Institute. Luo, Z., & Juang, C. H. (2012). Efficient reliability-based design of drilled shafts in sand considering spatial variability. Journal of GeoEngineering, 7(2), 59-68. Mahmoud, M. A. A. N. (2013). Reliability of using standard penetration test (SPT) in predicting properties of silty clay with sand soil. International Journal of Civil and Structural Engineering, 3(3), 545-556. doi:10.6088/ijcser.201203013050 Meyerhoff, G. G. (1976). Bearing capacity and settlement of pile foundation, The Eleventh Terzaghi Lecture. Journal of The Geotechnical Engineering Division, 102(3), 197-228. Ministry of Sciences and Technology, Vietnamese Government. (2014). TCVN 10304:2014. Móng cọc - Tiêu chuẩn thiết kế [National Standard TCVN 10304:2014. Pile foundation - Design standard]. Hanoi, Vietnam: Ministry of Sciences and Technology, Vietnamese Government. Phoon, K. K., & Kulhawy, F. H. (1999). Characterization of geotechnical variability. Canadian Geotechnical Journal, 36(4), 612-624. Shioi, Y., & Fukui, J. (1982). Application of N-values to design of foundation in Japan. In Proceedings of the second European symposium on penetrating testing, Penetration testing 1 (pp. 159-164). Amsterdam, Netherlands: CRC Press. 64 Duong H. Tham, Truong N. Manh. Ho Chi Minh City Open University Journal of Science, 11(1), 45-64 Skempton, A. W. (1986). No access standard penetration test procedures and the effects in sands of overburden pressure, relative density, particle size, ageing and overconsolidation. Géotechnique, 36(3), 425-447. doi:10.1680/geot.1986.36.3.425 Truong, M. N. (2017). Assessment of reliability of N-SPT numbers in predicting the bearing capacity of precast pile installed into cohesive soil in District 1, Ho Chi Minh City (Unpublished master’s thesis). Ho Chi Minh City Open University, Ho Chi Minh, Vietnam. Vanmarcke, E. H. (1977). Probabilistic modeling of soil properties. Journal of Geotechnical Division, ASCE, 103(11), 1227-1246. Vanmarcke, E. H. (1983). Random fields: Analysis and synthesis. Cambridge, MA: The MIT Press. Zekkos, D. P., Bray, J. D., & Der Kiureghian, A. (2004). Reliability of shallow foundation design using the standard penetration test. In A.V. Fonseca & P. W. Mayne (Eds), Geotechnical and geophysical site characterization (pp. 1575-1582). Porto, Portugal: Proceedings ISC-2 on geotechnical and geo-physical site characterization.
File đính kèm:
 predicting_the_bearing_capacity_of_pile_installed_into_cohes.pdf
predicting_the_bearing_capacity_of_pile_installed_into_cohes.pdf

