Phương pháp tối ưu đàn kiến dóng hàng toàn cục các mạng tương tác protein

 SPINAL. 
Phƣơng pháp tối ƣu đàn kiến (Ant Colony Optimization - ACO) [26] là cách tiếp cận metaheuristic, đƣợc giới thiệu 
bởi Dorigo năm 1991 đang đƣợc nghiên cứu và ứng dụng rộng rãi cho các bài toán tối ƣu t hợp khó. Bài báo này đề thuật 
toán ACOPPI sử dụng phƣơng pháp tối ƣu đàn kiến, kết hợp với thủ tục rebuild của FastNA nhƣ một thủ tục tìm kiếm cục 
bộ. Thực nghiệm cho thấy thuật toán đề xuất có điểm dóng hàng tốt hơn so với các thuật toán SPINAL, FastNA. 
Phần còn lại của bài báo đƣợc t chức nhƣ sau. Mục 2 phát biểu bài toán dóng hàng mạng và giới thiệu một số 
vấn đề liên quan. Thuật toán ACOPPI đƣợc trình bày trong mục 3. Mục 4 mô tả thực nghiệm so sánh ACOPPI với 
FastNA và SPINAL. Các kết luận và công việc tiếp theo đƣợc trình bày trong mục cuối. 
II. BÀI TOÁN DÓNG HÀNG MẠNG VÀ CÁC VẤN ĐỀ LIÊN QUAN 
Giả sử và là hai mạng tƣơng tác protein, trong đó ký hiệu tập các nút mô tả 
các protein trong mạng tƣơng ứng; ký hiệu tập các cạnh mô tả mối quan hệ tƣơng tác giữa các protein 
trong các mạng . Không giảm t ng quát, ta xem | | | | trong đó | | ký hiệu số phần tử của tập . 
Đỗ Xuân Quyền, Nguyễn Hoàng Đức, Thái Đình Phúc, Đỗ Đức Đông 627 
Dóng hàng mạng là tìm một đơn ánh từ vào tốt nhất theo một tiêu chí đánh giá nào đó. Hiện nay chƣa có 
định nghĩa rõ ràng cho tiêu chí này, dƣới đây phát biểu toán học cho định nghĩa bài toán dóng hàng theo tiêu chí thông 
dụng đƣợc dùng trong [1,4,5,14, 23]. 
Định nghĩa 1: (Dóng hàng mạng) Đồ thị là một mạng dóng hàng của hai đồ thị nếu nó 
thỏa mãn: 
i) Mỗi nút của đƣợc ký hiệu là tƣơng ứng với một cặp nút thuộc và thuộc . 
ii) Hai nút phân biệt và 
 thuộc thì 
 và 
iii) Cạnh 
 thuộc nếu và chỉ nếu ( 
 và 
 . 
Định nghĩa 2: Một dóng hàng mạng là lời giải của bài toán dóng hàng toàn cục của các mạng 
proteins nếu nó cực đại global network alignment score (GNAS) cho bởi: 
 | | ∑ (1) 
trong đó là tham số cân bằng giữa sự tƣơng đồng về tô pô mạng và sự tƣơng đồng trình tự giữa các 
nút, giá trị ( )đƣợc tính xấp xỉ dựa trên BLAST bit-scores hoặc E-values. 
Trong [1] Aladag và Erten [1] đã chứng minh bài toán tìm dóng hàng tối ƣu này là NP-hard. 
III. THUẬT TOÁN ACOPPI 
Khi áp dụng phƣơng pháp tối ƣu đàn kiến giải một bài toán cụ thể, cần giải quyết các vấn đề sau: 
- Cách xây dựng hành trình của mỗi kiến; 
- Chọn quy tắc cập nhật mùi. 
3.1. Cách xây dựng hành trình của mỗi kiến 
 Mỗi kiến xây dựng hành trình tƣơng ứng với việc tạo ra một lời giải của bài toán. Trong bài toán này, khi kiến 
xây dựng xong một hành trình cũng tƣơng ứng với việc tạo ra một phƣơng án dóng hàng mạng. Để kiến xây dựng hành 
trình, đầu tiên ta khởi tạo là rỗng. Sau đó, ta lặp lại công việc sau cho tới khi tất cả các nút của đều đƣợc ghép: 
kiến sẽ lựa chọn một nút (chƣa đƣợc ghép) thuộc , đồng thời xác định nút (chƣa đƣợc ghép) thuộc để ghép với 
và thêm nút vào . Nút đƣợc lựa chọn với tiêu chí là nút mang nhiều thông tin nhất, là nút có nhiều cạnh 
nối với các nút đã đƣợc ghép đƣợc trong . Nút đƣợc lựa chọn ngẫu nhiên với xác suất lựa chọn nút với 
nút là: 
 {
∑ 
 (2) 
Trong đó là giá trị thông tin heuristic, là hai tham số quyết định đến sự ảnh 
hƣởng tƣơng quan giữa thông tin mùi và thông tin heuristic, R là tập các đỉnh thuộc mà chƣa đƣợc ghép . 
Sau khi mỗi kiến xây dựng xong một hành trình, tƣơng ứng với một phƣơng án dóng hàng mạng, phƣơng án 
này sẽ đƣợc cải tiến nhờ thủ tục rebuild trong thuật toán FastNA [25]. 
3.2. Cập nhật mùi 
 Vết mùi thể hiện thông tin học tăng cƣờng qua mỗi vòng lặp. Trong bài toán này, đánh giá độ tốt khi ghép 
nút với nút . Thuật toán ACOPPI sử dụng phƣơng pháp cập nhật mùi SMMAS [27], đây là cách cập nhật 
mùi đơn giản và hiệu quả, cụ thể: 
 với {
3.3. Mô tả thuật toán 
Dữ liệu đầu vào bao gồm: Đồ thị , tham số , Sự tƣơng đồng trình tự giữa các nút tƣơng ứng 
của . Với mỗi tập con các cặp nút của tập , ký hiệu 
 { } 
 { 
 } 
Kết quả ra là một dóng hàng toàn cục . 
Lƣợc đồ thuật toán trong Hình 1 và đƣợc thực hiện theo các bƣớc sau: 
Bước 1. Khởi tạo: , | | 
Khởi tạo ma trận mùi với | | | | 
Bước 2. Thuật toán thực hiện chạy trong nhiều vòng lặp tiến hóa, điều kiện dừng có thể thiết đặt là giới hạn số vòng lặp 
tiến hóa hoặc giới hạn thời gian chạy. Trong mỗi vòng lặp tiến hóa, sẽ có n_ants kiến xây dựng hành trình, mỗi kiến 
thực hiện xây dựng hành trình nhƣ sau: 
628 PHƢƠNG PHÁP TỐI ƢU ĐÀN KIẾN DÓNG HÀNG TOÀN CỤC CÁC MẠNG TƢƠNG TÁC PROTEIN 
Lặp với tới | | //mỗi kiến xây dựng hành trình 
 2.1. Kiến chọn nút trong 
 có nhiều cạnh nối với các nút của 
 2.2. Kiến tìm nút j trong 
 để ghép với theo (2) 
2.3. B sung vào ; 
2.4. Cập nhật dựa trên ; 
2.5. Cải tiến lời giải do kiến xây dựng bằng thủ tục rebuild; 
Bước 3. Chọn lời giải của kiến có kết quả tốt nhất tính theo (1); 
Bước 4. Cập nhật mùi . 
Algorithm 1 ACOPPI 
Input: Đồ thị 1: ( ) Đồ thị 2: ( ) 
Sự tƣơng đồng trình tự giữa các nút: 
Tham số cân bằng 
Output: Dóng hàng mạng 
Begin 
Khởi tạo ma trận mùi và các tham số; 
while (điều kiện kết thúc) do 
for ant = 1 to n_ants do 
 for to | | do 
 = next_node_align( ); // chọn nút i có nhiều cạnh ghép với thành 
 = best_node_align( ); // kiến tìm nút để dóng hàng với 
Update( )// 
Update( // cập nhật các cạnh của 
 end-for 
 Cải tiến lời giải do kiến xây dựng bằng thủ tục rebuild; 
end-for 
 Update(GNAS); //chọn kết quả tốt nhất 
 Update( );// cập nhật mùi 
end-while 
End 
Hình 1. Lƣợc đồ thuật toán ACOPPI 
IV. THỰC NGHIỆM, SO SÁNH KẾT QUẢ VỚI PHƯƠNG PHÁP SPINAL VÀ FastNA 
 Chúng tôi tiến hành thực nghiệm với các bộ dữ liệu mà SPINAL và FastNA dùng thực nghiệm theo tiêu chí 
GNAS, từ đó làm cơ sở để so sánh hiệu quả với hai phƣơng pháp này. 
4.1. Thực nghiệm 
Bảng 1. Thông tin về dữ liệu 
Dữ liệu Số lƣợng protein (số nút) Số lƣợng tƣơng tác (số cạnh) 
Ce 2805 4495 
Dm 7518 25635 
Sc 5499 31261 
Hs 9633 34327 
Với 4 bộ dữ liệu mạng PPI: Saccharomyces cerevisiae (sc), Drosophila melanogaster (dm), Caenorhabditis 
elegans (ce) và Homo sapiens (hs). Các dữ liệu này lấy từ [20] với số protein (số nút) và tƣơng tác (số cạnh) đƣợc cho 
trong bảng 1. Thực nghiệm trên 6 cặp mạng khác nhau (ce-dm, ce-hs, ce-sc, dm-hs, dm-sc, hs-sc. Tham số nhận 5 giá 
trị lần lƣợt bằng 0.3, 0.4, 0.5, 0.6, 0.7 nhƣ trong [1]. Số kiến sử dụng là n_ants = 10 kiến và số vòng lặp tiến hóa là 100. 
Với mỗi cặp mạng PPI và một tham số , chúng tôi cho chƣơng trình ACOPPI chạy 20 lần, thống kê kết quả tốt 
nhất, tồi nhất, trung bình của 20 lần chạy. Ngoài ra, chúng tôi thống kê cả độ lệch chuẩn để đánh giá sự n định của 
thuật toán. 
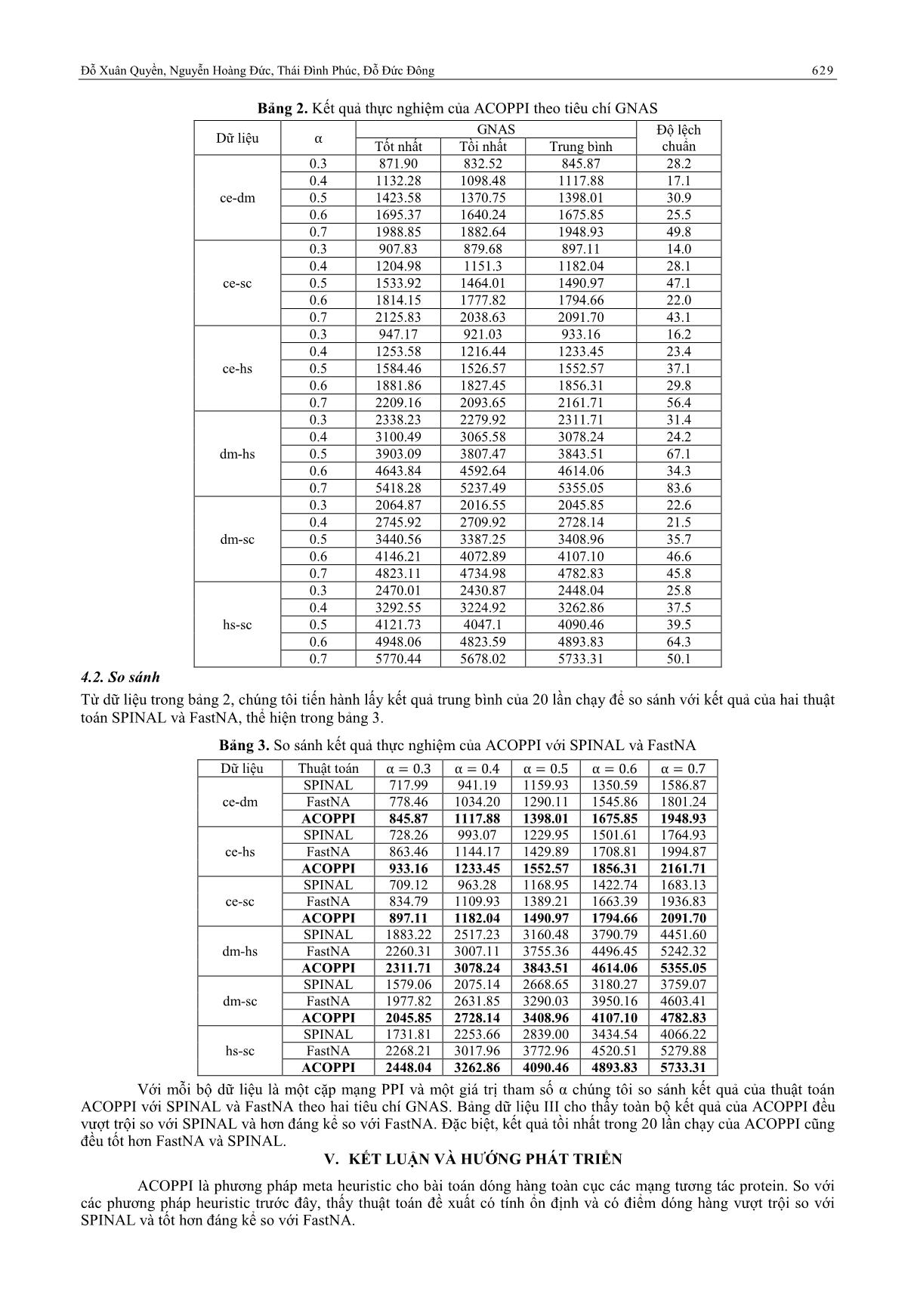
Kết quả thực nghiệm cho thấy chỉ có 03 bộ dữ liệu có độ lệch chuẩn trên 5% (ce-dm, =0.4; dm-hs, =0.3; ce-
hs, =0.3), còn lại đều dƣới 5%. Điều đó cho thấy thuật toán tƣơng đối n định. 
Đỗ Xuân Quyền, Nguyễn Hoàng Đức, Thái Đình Phúc, Đỗ Đức Đông 629 
Bảng 2. Kết quả thực nghiệm của ACOPPI theo tiêu chí GNAS 
Dữ liệu 
GNAS Độ lệch 
chuẩn Tốt nhất Tồi nhất Trung bình 
ce-dm 
0.3 871.90 832.52 845.87 28.2 
0.4 1132.28 1098.48 1117.88 17.1 
0.5 1423.58 1370.75 1398.01 30.9 
0.6 1695.37 1640.24 1675.85 25.5 
0.7 1988.85 1882.64 1948.93 49.8 
ce-sc 
0.3 907.83 879.68 897.11 14.0 
0.4 1204.98 1151.3 1182.04 28.1 
0.5 1533.92 1464.01 1490.97 47.1 
0.6 1814.15 1777.82 1794.66 22.0 
0.7 2125.83 2038.63 2091.70 43.1 
ce-hs 
0.3 947.17 921.03 933.16 16.2 
0.4 1253.58 1216.44 1233.45 23.4 
0.5 1584.46 1526.57 1552.57 37.1 
0.6 1881.86 1827.45 1856.31 29.8 
0.7 2209.16 2093.65 2161.71 56.4 
dm-hs 
0.3 2338.23 2279.92 2311.71 31.4 
0.4 3100.49 3065.58 3078.24 24.2 
0.5 3903.09 3807.47 3843.51 67.1 
0.6 4643.84 4592.64 4614.06 34.3 
0.7 5418.28 5237.49 5355.05 83.6 
dm-sc 
0.3 2064.87 2016.55 2045.85 22.6 
0.4 2745.92 2709.92 2728.14 21.5 
0.5 3440.56 3387.25 3408.96 35.7 
0.6 4146.21 4072.89 4107.10 46.6 
0.7 4823.11 4734.98 4782.83 45.8 
hs-sc 
0.3 2470.01 2430.87 2448.04 25.8 
0.4 3292.55 3224.92 3262.86 37.5 
0.5 4121.73 4047.1 4090.46 39.5 
0.6 4948.06 4823.59 4893.83 64.3 
0.7 5770.44 5678.02 5733.31 50.1 
4.2. So sánh 
Từ dữ liệu trong bảng 2, chúng tôi tiến hành lấy kết quả trung bình của 20 lần chạy để so sánh với kết quả của hai thuật 
toán SPINAL và FastNA, thể hiện trong bảng 3. 
Bảng 3. So sánh kết quả thực nghiệm của ACOPPI với SPINAL và FastNA 
 Dữ liệu Thuật toán 
ce-dm 
SPINAL 717.99 941.19 1159.93 1350.59 1586.87 
FastNA 778.46 1034.20 1290.11 1545.86 1801.24 
ACOPPI 845.87 1117.88 1398.01 1675.85 1948.93 
ce-hs 
SPINAL 728.26 993.07 1229.95 1501.61 1764.93 
FastNA 863.46 1144.17 1429.89 1708.81 1994.87 
ACOPPI 933.16 1233.45 1552.57 1856.31 2161.71 
ce-sc 
SPINAL 709.12 963.28 1168.95 1422.74 1683.13 
FastNA 834.79 1109.93 1389.21 1663.39 1936.83 
ACOPPI 897.11 1182.04 1490.97 1794.66 2091.70 
dm-hs 
SPINAL 1883.22 2517.23 3160.48 3790.79 4451.60 
FastNA 2260.31 3007.11 3755.36 4496.45 5242.32 
ACOPPI 2311.71 3078.24 3843.51 4614.06 5355.05 
dm-sc 
SPINAL 1579.06 2075.14 2668.65 3180.27 3759.07 
FastNA 1977.82 2631.85 3290.03 3950.16 4603.41 
ACOPPI 2045.85 2728.14 3408.96 4107.10 4782.83 
hs-sc 
SPINAL 1731.81 2253.66 2839.00 3434.54 4066.22 
FastNA 2268.21 3017.96 3772.96 4520.51 5279.88 
ACOPPI 2448.04 3262.86 4090.46 4893.83 5733.31 
Với mỗi bộ dữ liệu là một cặp mạng PPI và một giá trị tham số chúng tôi so sánh kết quả của thuật toán 
ACOPPI với SPINAL và FastNA theo hai tiêu chí GNAS. Bảng dữ liệu III cho thấy toàn bộ kết quả của ACOPPI đều 
vƣợt trội so với SPINAL và hơn đáng kể so với FastNA. Đặc biệt, kết quả tồi nhất trong 20 lần chạy của ACOPPI cũng 
đều tốt hơn FastNA và SPINAL. 
V. KẾT LUẬN VÀ HƯỚNG PHÁT TRIỂN 
ACOPPI là phƣơng pháp meta heuristic cho bài toán dóng hàng toàn cục các mạng tƣơng tác protein. So với 
các phƣơng pháp heuristic trƣớc đây, thấy thuật toán đề xuất có tính n định và có điểm dóng hàng vƣợt trội so với 
SPINAL và tốt hơn đáng kể so với FastNA. 
630 PHƢƠNG PHÁP TỐI ƢU ĐÀN KIẾN DÓNG HÀNG TOÀN CỤC CÁC MẠNG TƢƠNG TÁC PROTEIN 
Trong [1], các tác giả có đề xuất một phiên bản của SPINAL cho tiêu chí GOC. Trong thời gian tới, chúng tôi 
sẽ nghiên cứu, phát triển ACOPPI theo hƣớng này. 
VI. LỜI CẢM ƠN 
 Bài báo đƣợc hoàn thành trong khuôn kh của đề tài KHCN cấp ĐHQGHN, Mã số đề tài: QG.15.21. 
TÀI LIỆU THAM KHẢO 
[1] Aladag, A. E. and Erten,C. (2013), SPINAL: scalable protein interaction network alignment. Bioinformatics, Vol. 29 no 7, 
917–924 
[2] Bader, G. D. and Hogue, C. W. (2002), Analyzing yeast protein-protein interaction data obtained from different sources. Nat. 
Biotechnol., 20, 991–997. 
[3] Banks, E. et al., (2008), NetGrep: fast network schema searches in interactomes. Genome Biology, 9,R138 
[4] Chindelevitch, L. et al. (2010), Local optimization for global alignment of protein interaction networks. In: Pacific Symposium 
on Biocomputing, Hawaii, USA, pp. 123–132 
[5] Chindelevitch L. et al. (2013), Optimizing a global alignment of protein interaction networks, Bioinformatics ,Vol. 29 no. 21, 
2765–2773 
[6] Dost, B. et al. (2008), QNet: a tool for querying protein interaction networks. J. Comput. Biol., 15, 913–925 
[7] Dutkowski, J. and Tiuryn, J. (2007), Identification of functional modules from conserved ancestral protein–protein interactions. 
Bioinformatics, 23, i149–i158. 
[8] Han, J. D. et al. (2004), Evidence for dynamically organized modularity in the yeast protein-protein interaction network. 
Nature, 430, 88–93. 
[9] B. H. Junker and F. Schreiber, Analysis of Bological Networks, wiley, 2008 
[10] Kelley, B. P. et al. (2003), Conserved pathways within bacteria and yeast as revealed by global protein network alignment. 
Proc. Natl Acad. Sci. USA, 100, 11394–11399. 
[11] Kelley, B. P. et al. (2004), Pathblast: a tool for alignment of protein interaction networks. Nucleic Acids Res., 32,83–88. 
[12] Koyuturk, M. et al. (2006), Pairwise alignment of protein interaction networks. J. Comput. Biol., 13, 182–199. 
[13] Kuchaiev, O. et al. (2010), Topological network alignment uncovers biological function and phylogeny. J. R. Soc. Interface., 7, 
1341–1354. 
[14] Kuchaiev, O. and Przulj, N. (2011) Integrative network alignment reveals large regions of global network similarity in yeast 
and human. Bioinformatics, 27, 1390–1396. 
[15] Kuhn HW: The Hungarian Method for the assignment problem. Naval Res Logistics Q 1955, 2:83-97. 
[16] Liao, C.S. et al. (2009) IsoRankN: spectral methods for global alignment of multiple protein networks. Bioinformatics, 25, 
i253–i258. 
[17] Memisevic,V. and Przulj,N. (2012), C-graal: common-neighbors-based global graph alignment of biological networks. Integr. 
Biol., 4, 734–743. 
[18] Milenkovic, T. et al. (2010), Optimal network alignment with graphlet degree vectors. Cancer Inform., Vol.9, 121–137. 
[19] Narayanan, M. and Karp, R. M. (2007), Comparing protein interaction networks via a graph match-and-split algorithm. J. 
Comput. Biol., Vol. 14, 892–907. 
[20] Park, D. et al. (2011) IsoBase: a database of functionally related proteins across PPI networks. Nucleic Acids Res., 39, 295–300 
[21] Remm, M. et al. (2001), Automatic clustering of orthologs and in-paralogs from pairwise species comparisons. J. Mol. Biol., 
314, 1041–1052. 
[22] Sharan, R. et al. (2005), Conserved patterns of protein interaction in multiple species. Proc. Natl Acad. Sci. USA, 102, 1974–
1979. 
[23] Singh, R. et al. (2008), Global alignment of multiple protein interaction networks. In: Pacific Symposium on Biocomputing. 
pp. 303–314. 
[24] Zaslavskiy, M. et al. (2009) Global alignment of protein-protein interaction networks by graph matching methods. 
Bioinformatics, Vol.25, 259–267. 
[25] Do, D. D. et al. (2015), An efficient algorithm for global alignment of protein-protein interaction networks. Int. Conf. ATC 
2015, pp. 332-336. 
[26] M. Dorigo and T. Stutzle. Ant Colony Optimization. The MIT Press, Cambridge, Masachusetts, 2004. 
[27] Do, D. D., Dinh, Q. H, & Hoang, X. H. (2008). On the pheromone update rules of antcolony optimization approaches for the 
job shop scheduling problem. In Bui, T. D., Ho,T. V, Ha, Q. T., editors, The 11th Paci_c Rim International Conference on 
Multi-Agents:Intelligent Agents and Multi-Agent Systems, volume 5357 of Lecture Notes in ComputerScience, 153-160, 
Springer, Heidelberg. 
AN EFFICIENT ANT COLONY OPTIMIZATION FOR GLOBAL 
ALIGNMENT OF PROTEIN-PROTEIN INTERACTION NETWORK 
Do Xuan Quyen, Nguyen Hoang Duc, Thai Dinh Phuc, Do Duc Dong 
ABSTRACT— Global alignment of protein-protein interaction (PPI) network provides helpful information to discover features of 
protein, therefore the problem has been well studied worldwide. We present an effective metaheuristics algorithm ACOPPI, to tackle 
this problem. The algorithm applies Ant Colony Optimization (ACO) method to align PPI network combined with local search. 
Based on experiments, our algorithm showed better results than the published SPINAL algorithm and fastNA algorithm.