Phương pháp số giải một số bài toán biên trong miền vô hạn

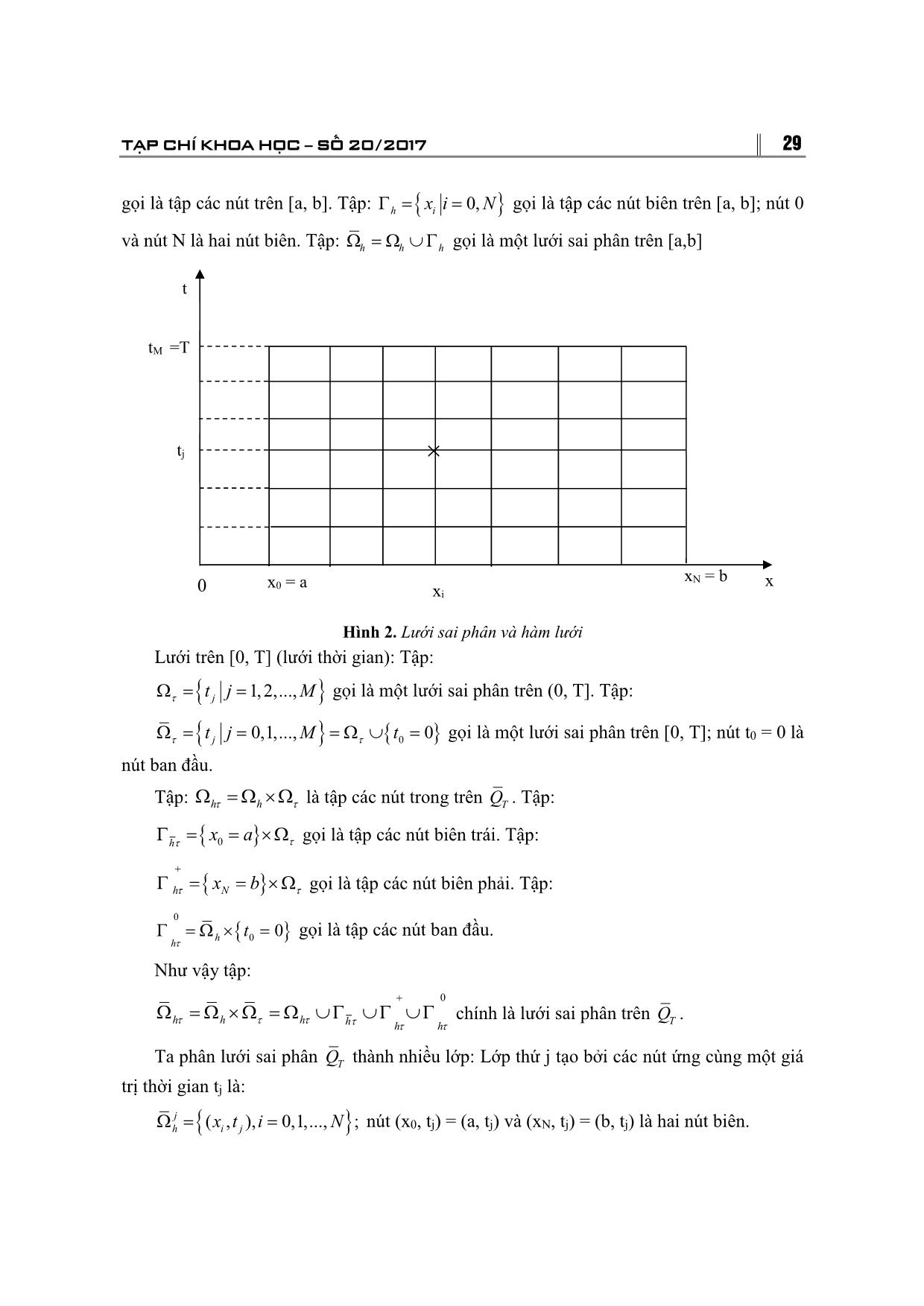
ỌC SỐ 20/2017   31 
 4M x 2 
 Xét miền bị chặn  x L,0 t T . Nhận thấy  W (x,t) a 2t  là nghiệm 
  2 
 L 2 
của phương trình (2.1) 
 Ta có   W( x ,0) v ( x ,0) W ( x ,0) 0  
 W(,) L t v (,)2 L t M v (,)0 L t  
 Áp dụng nguyên lý cực đại của hàm W (x,t) v(x,t)  và miền bị chặn  x L,0 t T. 
 Trong miền ấy, hàm W (x,t) v(x,t)  đạt giá trị nhỏ nhất tại t 0  hoặc tại  x L . Vậy 
 4M x 2 
giá trị nhỏ nhất ấy không âm W (x,t) v(x,t) 0  hay  v W  tức là  v a 2t . 
 2 
 L 2 
 Xét hàm  v  tại một điểm cố định  (x0 ,t0 )  nào đó. Cho  L 0  ta được  v(x0 ,t0 ) 0 , vì 
(x0 ,t0 )  là một điểm tùy ý nên ta có  v(x,t) º 0  u1 º u2  (đpcm). 
2.3.3. Giải bài toán Cauchy 
 Sử dụng phương pháp tách biến. 
 Ta xẽ tìm nghiệm của bài toán Cauchy (2.6), (2.7) dưới dạng  u(x,t) X (x).T (t)  thế 
biểu thức đó vào phương trình (2.6) ta đi đến hai phương trình sau: 
 T  a 2T 0 
 X  X 0  
 Trong đó    là một hằng số. 
 2
 Nghiệm của phương trình đầu là  T(t) e  a t . Vì tại mỗi điểm  x  của thanh nhiệt độ 
u(x,t)   không  thể  lớn  hơn  vô  cùng  khi  t    0   và  đặt   2   ta  được  
 2 2
T(t) e a t ,  X (x) Acos x B sin x , trong đó A, B là những hằng số có thể phụ thuộc 
 2 a2t
tham số  , vậy u (x,t) e A( )cos x B( )sin x với  cố định đều là nghiệm 
riêng của phương trình (2.6). Vậy ta được một hệ nghiệm riêng phụ thuộc tham số  . 
 2
 n 
 Khi giải bài toán hỗn hợp với các điều kiện biên bằng không, ta có    n    
 l 
n 1,2,...  Khi đó ta tìm nghiệm của bài toán dưới dạng chuỗi hàm. Ở đây   có thể lấy mọi 
giá trị không âm, do đó tham số   có thể lấy mọi giá trị thuộc  ,  .  
 Ta sẽ tìm nghiệm của bài toán dưới dạng: 
32   TRƯỜNG ĐẠI HỌC THỦ ĐÔ HÀ NỘI 
 2 2
 u(x,t) u (x,t)d e a t A( )cos x B( )sin x d             (2.8) 
  
 Dễ thấy hàm u(x,t)  cho bởi (2.8) cũng là nghiệm riêng của phương trình (2.6). Nếu tích 
phân ấy hội tụ đều và có thể lấy đạo hàm dưới dấu tích phân đó một lần đối với t  hai lần đối 
với  x . 
 Ta chọn  A( ), B( )  sao cho (2.8) thoả mãn điều kiện đầu (2.7) 
 u (x) A( )cos x B( )sin xd  
 t 0 
 1 
 A( ) ( )cos  d  
 2 
 1 
 B( ) ( )sin  d  
 2 
 1 2a2t 
thế vào (2.3), ta suy ra    u(x,t) e cos ( x)d ( ) d            (2.9)        
 2 
  x
 Đổi biến     
 a t
 2 2 1 2 1
 e a t cos ( x)d e  cos  d () . 
 a t a t
 2 2
 Trong đó  ( ) e  cos  d      e  sin  d  (ở đây có thể lấy 
đạo hàm dưới dấu tích phân được vì tích phân sau cùng hội tụ đều). Bằng cách lấy tích phân 
từng phần, ta được  
 2 1 2  2 
    e  sin  d e  sin  e  cos  d    
 2 2 2
 2  2
  ()   
    ln   ln C   C.e 4 . Trong đó,  C  là một hằng số 
 () 2 4
 2
tuỳ ý. Để xác định  C  ta cho   0   (0) C  lại vì    0 e  d  (tích phân 
poisson, tính  I(0)2  bằng cách chuyển sang toạ độ cực)  
TẠP CHÍ KHOA HỌC SỐ 20/2017   33 
 2 2
  x  x 
 2 2 
 () e 2 a t e a t cos ( x)d e 2 a t . 
 a t
 2
  x 
 1 
 Vậy công thức (2.10) có thể viết:  u(x,t) ( )e 2a t d                  (2.10) 
 2a t 
 Chứng minh  limt 0 u(x,t) x . 
  x
 Bằng cách đổi biến  s  suy ra ta có thể viết:  
 2a t
 1 2
 u(x,t) (x 2as t )e s ds . 
 1 2
 u(x,t) (x) | (x 2as t ) (x)| e s ds . 
 Vì  (x)  là một hàm bị chặn, nên ta giả sử  (x) M , suy ra 
 (x 2as t ) (x) 2M . 
 Suy ra  
 N N 
 2M 2 1 2 2M 2
 u(x,t) (x)   e s ds | (x 2as t ) (x)| e s ds e s ds  
 N N
 2
 Vì  e s ds  hội tụ nên tồn tại một số  N 0 đủ lớn sao cho: 
 N 
 2M 2  2M 2 
 e s ds ,  e s ds . 
 3 N 3
 N
 2 1 2 2
 Vậy  u(x,t) (x) | (x 2as t ) (x)| e s ds 
 3 N 3
 N 
 1 2 2  1 2
 e s ds e s ds  . đpcm. 
3 N 3 3 
 Chứng minh nghiệm (2.10) phụ thuộc liên tục vào điều kiện ban đầu. 
34   TRƯỜNG ĐẠI HỌC THỦ ĐÔ HÀ NỘI 
 Gọi   là nghiệm của phương trình (2.6) thoả mãn điều kiện ban đầu  u (x) . 
 u (x,t) t 0
Khi đó hiệu   là nghiệm của (2.6) thoả mãn  (u u) (x) (x) . 
 u(x,t) u (x,t) t 0
 2
  x 
 1 
 u(x,t) u (x,t) [ ( ) ( )] e 2a t d .   Nếu  (x) (x)       x   
 2a t 
thì 
 2 2
  x  x 
 1 1 
 | u(x,t) u (x,t) | | ( ) () | e 2a t d    e 2a t d  
 2a t 2a t 
hay | u(x,t) u (x,t) |    (đpcm). 
2.4. Phương pháp hệ vô hạn đối với các bài toán dừng 
 Trong phần này sẽ trình bày chi tiết phương pháp hệ vô hạn trên mô hình bài toán truyền 
nhiệt dừng trong thanh nửa vô hạn: 
         (ku'' ) du f ( x ), x 0,                         (2.11) 
 u(0) 0 , u ( ) 0  
với các giả thiết thông thường 
 2
   KkxKDdxDfxL0 () 1 , 0 () 1 , () (0,)  C (0,).       (2.12) 
 Nhận xét: Trong trường hợp k, d là các hằng số và f(x) có giá compac là 0, L  người ta 
dễ dàng  tìm được điều  kiện biên nhân tạo  chính xác  tại  x  =  L  nhờ  ánh  xạ Dirichlet-to-
Neumann. Khi f không  có giá compac nhưng  có dạng đặc biệt sao cho có thể tìm được 
nghiệm riêng của phương trình 
 "
 u cu f( c constant 0)  
điều kiện biên nhân tạo chính xác cũng có thể thiết lập được. Trong trường hợp tổng quát 
khi k, d, f chỉ thỏa mãn điều kiện (2.11) và hạn chế xét bài toán trong một khoảng hữu hạn 
nào đó 0, L  người ta không tìm được điều kiện chính xác tại x = L. Để giải quyết bài toán 
(2.11), (2.12) chúng tôi đưa vào lưới điểm cách đều  xi ih, 0,1... và xét lược đồ sai phân: 
 (ayx ) x dy f i i 1, 2,...
                                 (2.13) 
 y0  0 , yi 0, i .
TẠP CHÍ KHOA HỌC SỐ 20/2017   35 
trong đó: 
 ai k( x i h / 2), d i d ( x i ), f i f ( x i ) . 
 Viết lại lược đồ sai phân (2.13) trong dạng hệ phương trình sai phân ba điểm thông 
thường  
 A y C y By f, i 1,2,...
         i i 1 i i i 1 i            (2.14) 
 y0  0 , yi 0, i .
 Ở đây:  
 a a
         A i,,. B i 1 C A B d      (2.15) 
 ih2 i h 2 i i i i
 Đặt: 
 p0 q 0 0, r 0  0 ,  
 Ai B i f i
         pi , q i , r i ( i 1,2,...)        (2.16) 
 CCCi i i
ta viết hệ (2.14) trong dạng chính tắc của hệ vô hạn như sau: 
 yi p i y i 1 q i y i 1 r i , i 1,2,...
                  (2.17) 
 yi 0, i 
 Ta có:        0 1 p 0 q 0 1 và 
 di
         i 1 p i q i 0 ( i 1,2,...)          (2.18) 
 Ci
 Như vậy, hệ (2.17) là chính quy. Chính xác hơn, nó là hệ hoàn toàn chính qui vì dễ dàng 
kiểm tra rằng 
 D0
         i 2 (i 1,2,...)            (2.19) 
 D1 2 K 1 / h
 r r f
 Bây giờ xét  i . Từ (2.16), (2.17), ta có  i i . Từ các giả thiết (2.11) suy ra rằng: 
 i id i
fi
 0 , do đó tồn tại hằng số k* sao cho  fi K* d i  với mọi i. Vì thế điều kiện của định 
di
lý 2 được thỏa mãn và nghiệm vô hạn của (2.12) có thể tìm được bằng phương pháp cắt cụt. 
36   TRƯỜNG ĐẠI HỌC THỦ ĐÔ HÀ NỘI 
 Vấn đề đặt ra là cắt cụt hệ vô hạn đến cỡ nào để thu được nghiệm gần đúng với sai số 
cho trước. Dưới đây sẽ trả lời câu hỏi trên. 
 Ta sẽ tìm nghiệm của hệ (2.12) trong dạng 
         yi i 1 y i 1  i 1 , i 0,1,...,          (2.20) 
trong đó các hệ số được tính như sau: 
 1 0,  1  0,
 qi r i p i i          (2.21) 
 i 1 ,  i 1 ,i 1,2,...
 1 pi i 1 p i i
 Tương tự như trong trường hợp hệ phương trình sai phân ba điểm hữu hạn có thể chứng 
minh bằng quy nạp rằng  0 i 1 (i 0,1,...) . Do đó, từ điều kiện  yi 0  và từ (2.15) 
suy ra  i 0 khi i . 
 Xét hệ cắt cụt  
 yi p i y i 1 q i y i 1 r i , i 0,1,2,..., N
          (2.22) 
 yi 0, i N 1
 Định lý 4: Cho trước sai số  0 .Nếu 
 i
           ,i N 1                           (2.23) 
 1 i
thì ta có đánh giá sau đối với sai số của nghiệm của hệ vô hạn (2.12) so với nghiệm của hệ 
cắt cụt (2.17) 
         sup yi y i .                              (2.24) 
 i
 Chứng minh: Ký hiệu  zi y i y i .  Khi đó dễ dàng kiểm tra rằng  zi  thỏa mãn hệ vô  
hạn sau 
 zi i 1 z i 1 b i , i 0,1,...,                   (2.25) 
trong đó: 
 0,i 0,..., N ,
 bi  
 i 1 i N 1.
TẠP CHÍ KHOA HỌC SỐ 20/2017   37 
 Hệ này là hệ chính quy vì đối với nó  i 1 i 1 0  do 0 i 1 (i 0,1,...) như 
đã nói ở trên. Từ điều kiện (2.18) suy ra  bi  i  với mọi i = 0,1, Do đó, theo lý thuyết 
hệ vô hạn ta có đánh giá  zi  , i 0,1,... Định lý được chứng minh. 
 Nhận xét: Định lý trên cho phép ta trong quá trình tính các hệ số truy đuổi (2.16) xác 
định khi nào cắt cụt của hệ vô hạn (2.12) để đảm bảo rằng nghiệm của hệ cắt cụt sai khác so 
với nghiệm của hệ vô hạn không   quá cho trước. 
 Dưới đây chúng ta xét một ví dụ minh họa hiệu quả của việc sử dụng định lý trên. 
 Ví dụ. Xét bài toán: 
 ' 1 1
 1 sin2x u ' u e x (sin 2 x 1,5 c os2x/2+ )
 1 x 1+x  
 u(0) 1, u ( ) 0.
 Bài toán này có nghiệm đúng  u x e x . 
 Xây dựng hệ vô hạn (3.12) và cắt cụt nó khi định lý trên được thỏa mãn. Nghiệm của hệ 
cắt cụt được so sánh với các nghiệm chính xác. Kết quả tính toán trên lưới với h=0.1 và 
h=0.05 được cho trong các bảng dưới đây, trong đó  N  là cỡ của hệ được tự động cắt cụt, 
SS max yi u i,. u i u x i 
 0 i N  
 Bảng 1. h 0.1 
  N SS 
 0.01  59  0.0027 
 0.001  86  2.7761e-4 
 0.0001  116  2.8224e-4 
 Bảng 2. h 0.05 
    N   SS  
 0.01  117  0.0029 
 0.001  170  2.0347e-4 
 0.0001  224  7.0619e-5 
38   TRƯỜNG ĐẠI HỌC THỦ ĐÔ HÀ NỘI 
 Đồ thị của nghiệm đúng, nghiệm gần đúng với  h 0.05,  0.01 và hàm vế phải cho 
trong các Hình 3 và Hình 4.  
                                                                                  Hình 3. Nghiệm đúng và nghiệm xấp xỉ Hình  4. Hàm vế phải với h 0.05 và 
 với h 0.05 và  0.01    0.01  
 Trong quá trình tính toán ta nhận thấy  rằng các hệ số  i 0  rất nhanh và các hệ số  i  
có xu thế dần tới 1 nhưng tỷ số   i /(1 i )  tiến tới 0 cũng khá nhanh. Đồ thị các hệ số và tỷ 
số của chúng cho trong các Hình 5 – 7. 
   Hình 5. Các hệ số với Hình 6. Các hệ số  với 
 h 0.05 và  0.01   h 0.05 và  0.01  
TẠP CHÍ KHOA HỌC SỐ 20/2017   39 
  Hình 7. Tỷ số /(1 ) với h 0.05 và  0.01 
2.5. Phương trình parabolic trong thanh nửa vô hạn 
 Trong mục này chúng ta sẽ áp dụng kỹ thuật hệ vô hạn đã đề xuất ở mục trước cho bài 
toán biên-giá trị đầu cho phương trình parabolic.  
 a) Đầu tiên ta xét bài toán truyền nhiệt với hệ số hằng 
 u 2 u
 k, 0 x , t 0
   t  x2                 (2.26) 
 u( x ,0) 0, u (0, t ) 1, u ( , t ) 0.
 Bài toán này có nghiệm đúng là 
 2 
     u( x , t ) exp( 2 ) d  .                  (2.27) 
 x/ 2 kt
 Sử dụng lược đồ sai phân ẩn thuần túy trên lưới đều với bước lưới không gian là  h  và 
bước lưới thời gian là   ta dẫn được  bài toán về  hệ vô hạn trên mỗi lớp thời gian  j 1 
 ryj 1 (1 2 r ) y j 1 ry j 1 y j , i 1,2,...
   i 1 i i 1 i        (2.28) 
 j 1 j 1
 y0 1, yi 0, i ,
trong đó  r k / h2 , i, j  là chỉ số nút  theo không gian và thời gian. 
 Hệ (2.28) được xử lý tương tự như hệ (2.9). 
 Để thấy được tính ưu việt của phương pháp hệ vô hạn so với phương pháp lưới tựa đều 
được đề xuất và ứng dụng từ năm 2001 chúng tôi đã thực hiện tính toán theo hai phương 
 i
pháp: hệ vô hạn trên lưới đều và hệ hữu hạn trên lưới tựa đều  x ( i 0,..., N )  với 
 i N i
N 50 . Do mật độ các nút tựa đều rất thưa khi i 25  nên các profile thu được bị gãy khúc. 
Các  hình  8  và  hình  9  cho  các    profile  tính  bằng  hai  phương  pháp  nêu  trên  với 
40   TRƯỜNG ĐẠI HỌC THỦ ĐÔ HÀ NỘI 
k 10, 0.001. Từ các hình này ta thấy rõ ràng là kết quả tính trên lưới đều sử dụng hệ 
vô hạn cho kết quả tốt hơn. 
    Hình 8. Profiles u(,) x j với các j     Hình 9. Profiles u(,) x j với các j 
 khác nhau và  1 tính bằng hệ vô hạn  khác nhau và  1, sử dụng lưới tựa đều 
 b) Bài toán ô nhiễm khí quyển dừng do một nguồn điểm có cường độ không đổi Q 
gây ra tại điểm (0,  H )  đã được dẫn về bài toán 
     
 u w   0, x 0,           (2.29) 
  x g  z  x  z
 u Q z H , x 0,             (2.30) 
  
 ,z 0, 0, z ,             (2.31) 
 z
trong đó   là nồng độ khí thải,  u  là vận tốc gió theo chiều  x ,  wg  vận tốc rơi của khí thải 
do trọng trường,  f cường độ nguồn thải,   0  hệ số biến đổi,   hệ số khuếch tán theo 
chiều thẳng đứng,  0  hệ số hấp thụ của mặt đất. Lời giải số bài toán trên sử dụng lưới 
đều và hệ vô hạn đã được nghiên cứu, ở đó định lý tương tự như Định lý 4 với các giả thiết 
là tồn tại số  N  sao cho  0 i  , 0 i  1 với mọi i N  đã được chứng minh.  
 Một điều lý thú đã được chứng minh trong [2.29] là nếu hạn chế xét bài toán ô nhiễm 
trong miền có độ cao hữu hạn 0 z Z  và đặt điều kiện biên nhân tạo  (x, Z) 0  thì ta được 
  
nghiệm “non”, còn nếu đặt  (x, Z ) 0  thì ta được nghiệm “già” hơn nghiệm bài toán với 
 z
điều kiện biên  (x, ) 0 . 
 TẠP CHÍ KHOA HỌC SỐ 20/2017   41 
 3. KẾT LUẬN 
 Bài báo đã đề cập đến lý thuyết về phương pháp sai phân giải bài toán biên và bài toán 
 giá trị đầu, nghiên cứu phương pháp hệ vô hạn các phương trình đại số giải một số bài toán 
 một chiều không gian phụ thuộc hoặc không phụ thuộc thời gian, trong đó cốt lõi là cách xác 
 định khi nào thì cắt cụt hệ vô hạn để đảm bảo thu được nghiệm gần đúng với sai số cho 
 trước. Phương pháp này thể hiện ưu thế vượt trội so với phương pháp lưới tựa đều do các 
 nhà toán học Nga mới đề xuất năm 2001 trong các bài toán phụ thuộc thời gian, đặc biệt là 
 các bài toán  truyền sóng. 
 Trong khoảng thời gian ngắn, bài báo chưa thể đề cập đến nhiều thuật toán trong lý 
 thuyết toán học tính toán cũng như nhiều dạng bài toán biên khác nhau.  
 TÀI LIỆU THAM KHẢO 
1. Đặng Quang Á (2007), “Phương pháp hệ vô hạn các phương trình đại số đối với các bài toán 
 trong miền không giới nội”, Kỷ yếu Hội thảo Khoa học quốc gia lần III FAIR, Nha Trang. 
2. E.A.Alshina, N.N.Kalitkin and  S.L.Panchenko (2002), “Numerical solution of boundary value 
 problems in unbounded domains”, Math. Modelling, Vol.14, No 11, pp.10-22. 
3. A.B.Alshin,  E.A.Alshina,  A.A.Boltnev,  O.A.Kacher  and  P.V.Koryakin  (2004),  “Numerical 
 solution of initial-boundary value problems for Sobolev-type equations on quasi-uniform grids”. 
 Comput. Math. and Math. Phys., 44(3), pp.490-510. 
4. A.Samarskii (2001), The Theory of Difference Schemes. New York:. Marcel Dekker. 
5. T.Colonius (2004), “Modeling Artificial Boundary Conditions for Compressible Flow”. Annual 
 Review of Fluid Mechanics, 36, pp.315-345. 
 THE METHODS OF SETTLING A NUMBER OF 
 FINANCIAL BONDS 
 Abstract: The theory of boundary boundary problems in the infinite domain is one of the 
 important areas of modern differential equation theory. Many mechanical and physical 
 mathematical problems are posed in infinite domain, such as heat transfer in an infinite 
 bar, in an infinite range, the problem of spreading the exhaust in the vast atmosphere... 
 The problem is solved in a finite domain. Then a series of issues are set out to determine 
 how large a domain is and how to place the boundary conditions on the virtual boundary 
 to obtain an approximate solution of the problem in the infinite domain. Therefore, studying 
 and researching boundary problems in infinite domain is very important. Particularly in 
 the country, this is a relatively new field, almost no documents adequately addressed this issue. 
 Keywords: Boundary problem, infinite domain.