Phân tích xác suất dừng của việc lựa chọn uav thu thập năng lượng

u thập năng lượng từ tín hiệu tần số vô tuyến của thiết bị nguồn và 
sử dụng năng lượng thu thập được để khuếch đại và chuyển tiếp tín hiệu nhận được đến thiết 
bị đích. Như đã thấy trong Hình 1(b), tổng thời gian T để truyền tin từ thiết bị nguồn đến 
thiết bị đích được chia thành 3 giai đoạn. Trong suốt giai đoạn 1 kéo dài αT với 0 < α < 1 là 
hệ số chia thời gian, các UAV thu thập năng lượng từ tín hiệu tần số vô tuyến của thiết bị 
nguồn. Năng lượng mà UAV Ri, Ri  , thu hoạch được trong giai đoạn này là 
2
i iR S SR
EH TP h = , trong đó PS biểu thị công suất phát của thiết bị nguồn, η là hiệu suất 
chuyển đổi năng lượng, 
iSR
h là hệ số kênh truyền của tuyến S-Ri. Trong giai đoạn 2 kéo dài 
( )1 / 2T − , thiết bị nguồn phát tín hiệu xS đến các UAV. Ở cuối giai đoạn này, UAV tốt 
nhất Rb được chọn theo tiêu chí đã đề cập ở đầu phần này. UAV tốt nhất hoạt động như thiết 
bị chuyển tiếp để khuếch đại tín hiệu nguồn và phát tín hiệu được khuếch đại đến thiết bị 
đích trong giai đoạn 3 kéo dài ( )1 / 2T − . 
Trong giai đoạn 2, tín hiệu thu được tại UAV tốt nhất Rb có thể được biểu thị dưới dạng 
b b bR S SR R
y x h n= + , trong đó xS là tín hiệu được truyền bởi S với công suất phát PS, 
 2| |S SP x=  , bSRh là hệ số kênh truyền của tuyến S-Rb và bSRn là nhiễu tại Rb. Không mất 
tính tổng quát, nhiễu tại máy thu v với ,iv R D và Ri  được giả sử là nhiễu Gaussian 
Hồ Văn Khương 
36 
trắng cộng (Additive White Gaussian Noise - AWGN) với giá trị trung bình bằng 0 và phương 
sai N0, nghĩa là { } 0vn = và 
2
0{| | }vn N = . Khi đó, SNR tức thời của tuyến S-Rb là 
2
b bSR SR
h = (3) 
trong đó 
0
SP
N
 = là SNR được chuẩn hóa. 
Trong giai đoạn 3, UAV tốt nhất Rb tiêu thụ năng lượng thu thập được để chuyển tiếp 
tín hiệu nguồn được khuếch đại 
bR
x đến thiết bị đích với công suất phát như sau: 
( )
2
1 / 2
b
b b
R
R S SR
EH
P P h
T

= =
−
 (4) 
trong đó 
2
1

=
−
. 
Tín hiệu nguồn được khuếch đại 
bR
x , được truyền từ Rb đến D, và được biểu thị là 
b bR R
x y= , trong đó hệ số khuếch đại β được tính sao cho công suất phát của Rb là 
bR
P 
trong (4), nghĩa là 
 
 
2
22
0
b
b
bb
R
R
S SRR
x P
P h Ny


= =
+
 (5) 
Do đó, tín hiệu nhận được tại thiết bị đích được biểu thị dưới dạng 
b b b b b bD R R D D S SR R D R D R D
y x h n x h h h n n = + = + + , trong đó 
bR D
h là hệ số kênh truyền của 
tuyến Rb-D và nD là nhiễu tại D. Khi đó, SNR của tuyến S-Rb-D có thể được thể hiện như 
sau: 
2 2
2
2
2
0 0
b b
b
S SR R D
D
R D
P h h
h N N



=
+
 (6) 
Thay (5) vào (6) và sau một số phép đơn giản hóa, ta thu được 
2 2
2
2
2 0 0
0
b b
b
b
b b
S SR R D
D
S SR
R D
R R
P h h
N P h N
h N
P P
 =
+ +
 (7) 
Vì công suất phát PS lớn hơn nhiều so với công suất nhiễu N0 nên 
2
0 0
bR
N
P
= . Do đó, (7) 
có thể được tính gần đúng như sau: 
Phân tích xác suất dừng của việc lựa chọn UAV thu thập năng lượng 
37 
2 2
2
2 0
0
b b
b
b
b
S SR R D
D
S SR
R D
R
P h h
N P h
h N
P
 =
+
 (8) 
Thay thế 
bR
P trong (4) vào (8), ta thu được 
2 2
2
1
b b
b
SR R D
D
R D
h h
h



=
+
 (9) 
3. PHÂN TÍCH HIỆU NĂNG 
Để đánh giá nhanh hiệu năng của việc lựa chọn UAV thu thập năng lượng, biểu thức 
dạng tường minh chính xác của xác suất dừng được suy ra trong phần này. Nhắc lại rằng 
trong số M UAV thì chỉ có UAV tốt nhất Rb được chọn theo nguyên tắc lựa chọn từng phần 
mà cung cấp SNR lớn nhất trên tất cả các tuyến S-UAV. Do đó, chỉ số của UAV tốt nhất có 
thể được ký hiệu là arg max
i
R
SR
i
b 
 
= . Khi đó, SNR tại Rb được biểu diễn tương đương là 
max
b i
R
SR SR
i
 
 
= . Để thuận tiện trình bày, tất cả các UAV được giả sử là đặt đồng nhất, dẫn 
đến 
1 2
...
MSR SR SR SR
   = = = = mà là công suất fading của tuyến S-UAV. Đặt 
2
max
i
R
SR
i
X h
 
= , ta đạt được thống kê của X trong bổ đề sau. 
Bổ đề 1: CDF và PDF của X lần lượt được cho bởi 
( ) ( )
0
1 SR
qM x
q q
X M
q
F x C e

−
=
= − (10) 
( ) ( )
11
1
0
1 SR
qM x
q q
X M
qSR
M
f x C e


+− −
−
=
= − (11) 
trong đó x ≥ 0 và 
!
!( )!
q
M
M
C
q M q
=
−
 là hệ số nhị thức. 
Chứng minh: 
PDF của X được định nghĩa là 
( )  2Pr Pr max i
R
X SR
i
F x X x h x
 
= = (12) 
Vì tất cả các tuyến S-Ri là độc lập nên (12) được viết lại thành 
( )  ( )22
1
Pr
i
SRi
MM
X SR
h
i
F x h x F x
=
= = 
 (13) 
Thay CDF của 
2| |
iSR
h được cho trong (2) vào (13) với lưu ý rằng 
iSR SR
 = do phân 
bố đồng nhất của các UAV, ta thu được: 
Hồ Văn Khương 
38 
( ) 1 SR
M
x
XF x e

− 
= − 
 (14) 
Sử dụng khai triển nhị thức ( )
0
n
n m m n m
n
m
a b C a b −
=
+ = , ta có thể thu gọn (14) xuống (10), 
hoàn thành một phần của chứng minh. 
Lấy đạo hàm của (10) theo x, ta có thể thu được PDF của X giống hệt như (11), hoàn 
thành phần còn lại của chứng minh. ■ 
Dựa trên lý thuyết thông tin, SNR của tuyến S-Rb-D, D , nên lớn hơn một mức ngưỡng 
th để giữ kết nối đầu cuối tin cậy
1. Xác suất mà γD không lớn hơn mức ngưỡng đó được biết 
như xác suất dừng (OP), nghĩa là  ( )Pr
DD th th
OP F  = = . Sử dụng γD trong (9), ta 
có thể viết lại ( )
D th
F  ở dạng ngắn gọn như sau: 
( ) Pr
1D
th
th
XY
F
Y

 

 
 
= 
+ 
 (15) 
trong đó 
2 2
max
b i
R
SR SR
i
X h h
 
 = =
 và 
2
bR D
Y h= . 
Bổ đề 2: Biểu thức dạng tường minh chính xác của xác suất dừng của việc lựa chọn UAV 
thu thập năng lượng được cho bởi 
( ) ( )
( )
( )
( )
1
1
1 1
0
12
1 1 2
1
th
SR
D
q
M
q q thSR th
th M
qSR RD SR RD
qM
OP F C e K
q



 

   
+
− −
−
=
 +
= = − − 
 +
 (16) 
trong đó 
1 2
...
MR D R D R D RD
   = = = = và ( )1K  là hàm Bessel hiệu chỉnh bậc nhất loại hai. 
Chứng minh: 
Viết lại (15) như sau: 
( ) Pr
D
th th
thF Y X
 
 
 
  
= −  
 
 (17) 
Phương trình (17) có thể được đơn giản hóa bằng cách xem xét hai trường hợp của X là 
( )
( )
Pr ,
1,
D
th th
th
th
th
Y X
X
F X
X

 
   



  
 
− = 
 (18) 
1Dung lượng kênh truyền mà D có thể đạt được là ( )
1
log 1
2
D D

−
= + . Do đó, D giải mã thành 
công thông tin nguồn nếu dung lượng kênh truyền của nó lớn hơn hiệu suất phổ yêu cầu Cth. Điều này 
tương đương γD lớn hơn 
2 /(1 )
2 1thth
  −= − . 
Phân tích xác suất dừng của việc lựa chọn UAV thu thập năng lượng 
39 
Như vậy, xác suất dừng không điều kiện được biểu diễn như sau: 
( ) ( )
( )
( )
0
th
D
th
th
th X Y X
th
F f x dx F f x dx
x







  
= + − 
 (19) 
Thế FY(x) trong (2) vào phương trình trên và sau một số phép đơn giản hóa, ta có thể 
đơn giản hóa (19) hơn nữa như sau: 
( ) ( ) ( ) ( ) ( ) ( )
0
1 1
th
th th
RD th RD th
D
th th
x x
th X X XF f x dx e f x dx e f x dx

 
     

 
 

 − −
− −
= + − = − 
(20) 
Cần lưu ý rằng 
iR D RD
 = , Ri  , do phân bố đồng nhất của các UAV. Do đó, 
( ) /1 RDxYF x e
−= − được dùng trong (20). 
Bây giờ, thay fX(x) trong (11) vào (20), ta sẽ thu được 
( ) ( ) ( )
1
1
1
0
1 1
th
RD th SR
D
th
q
M x
q xq
th M
qSR
M
F C e dx

   





 + − − + − 
−
=
= − − (21) 
Bằng cách đổi biến tht x = − , (21) trở thành 
( ) ( )
( ) ( )111
1
0 0
1 1
thth
RD SRSR
D
q tq
M
q tq
th M
qSR
M
F C e e dt

  
 

+ + − − +− 
−
=
= − − (22) 
Sử dụng ( )4 1
0
x
xe dx K

 


− −
= trong [9, phương trình (3.324.1)] để tính tích 
phân cuối cùng trong (22), ta có thể biểu diễn (22) ở dạng tường minh chính xác như (16). 
Điều này hoàn thành việc chứng minh. ■ 
4. KẾT QUẢ MINH HỌA 
 Trong phần này, mô phỏng Monte-Carlo được thực hiện để đạt được các kết quả mô 
phỏng nhằm chứng minh tính hợp lệ của biểu thức lý thuyết được đề xuất trong (16) cũng như 
để có cái nhìn sâu sắc về độ tin cậy của việc lựa chọn UAV thu thập năng lượng. Một số thông 
số mô phỏng được cố định trong suốt phần này là tần số sóng mang fC = 900 MHz và số mũ 
suy hao đường truyền τ = 2 (tương ứng với suy hao đường truyền trong không gian tự do). 
Hình 2 minh họa xác suất dừng theo SNR được chuẩn hóa 0/SP N = khi khoảng 
cách của các tuyến (S-Ri, Ri-D) lần lượt là dSR = 100 m và dRD = 50 m; hệ số chia thời gian là 
α = 0,5; hiệu suất chuyển đổi năng lượng là η = 0,8; hiệu suất phổ yêu cầu là Cth = 0,1 bps/Hz. 
Hình này cho thấy sự trùng khớp giữa phân tích và mô phỏng, do đó, xác nhận tính chính xác 
của biểu thức đề xuất trong (16). Ngoài ra, độ tin cậy của tuyến S-Rb-D được cải thiện khi 
SNR được chuẩn hóa tăng. Hơn nữa, hiệu quả của việc lựa chọn UAV đã được chứng minh, 
mà dựa trên quan sát trong Hình 2 là số lượng UAV càng nhiều thì xác suất dừng càng thấp. 
Hồ Văn Khương 
40 
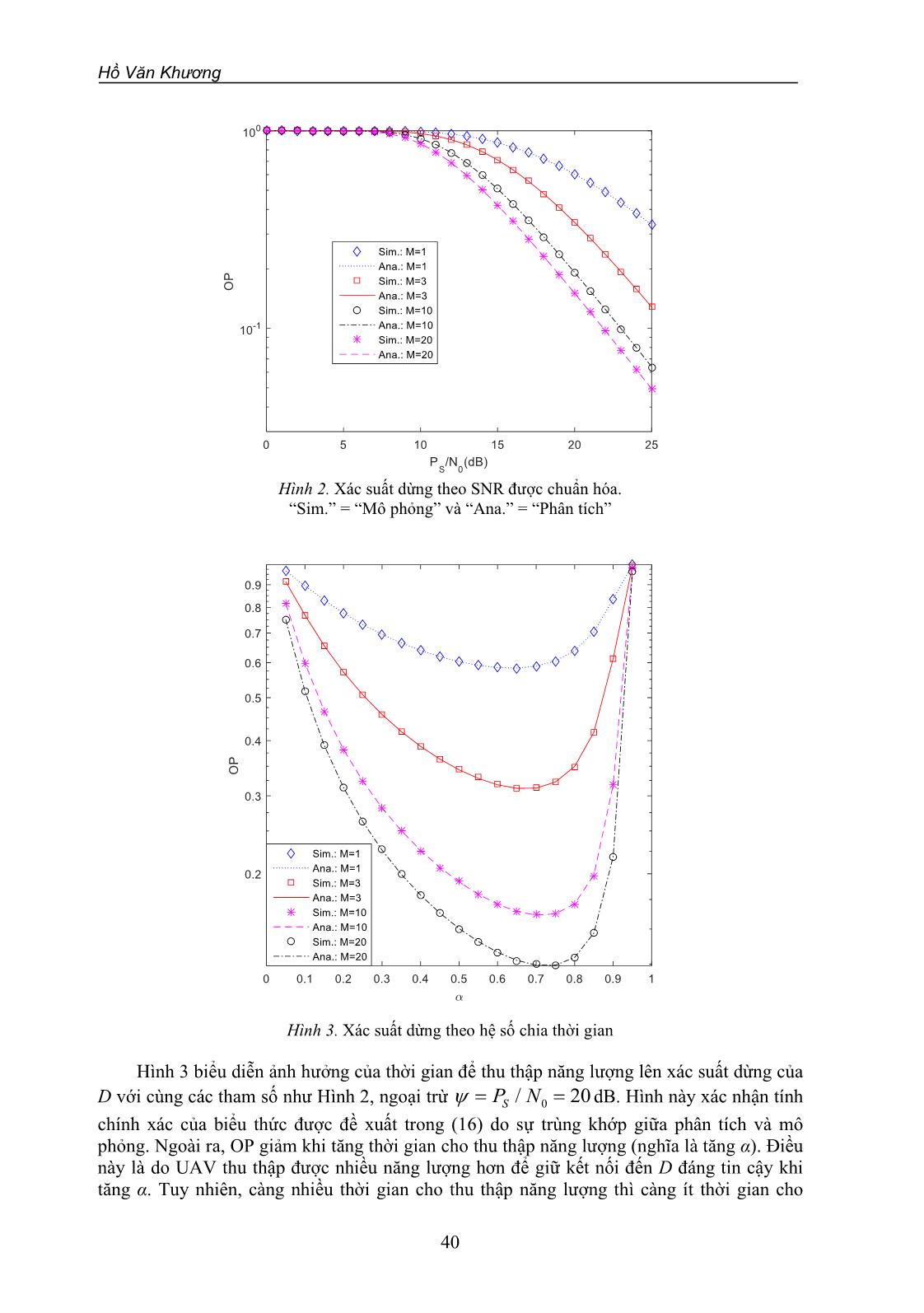
Hình 2. Xác suất dừng theo SNR được chuẩn hóa. 
“Sim.” = “Mô phỏng” và “Ana.” = “Phân tích” 
Hình 3. Xác suất dừng theo hệ số chia thời gian 
Hình 3 biểu diễn ảnh hưởng của thời gian để thu thập năng lượng lên xác suất dừng của 
D với cùng các tham số như Hình 2, ngoại trừ 0/ 20SP N = = dB. Hình này xác nhận tính 
chính xác của biểu thức được đề xuất trong (16) do sự trùng khớp giữa phân tích và mô 
phỏng. Ngoài ra, OP giảm khi tăng thời gian cho thu thập năng lượng (nghĩa là tăng α). Điều 
này là do UAV thu thập được nhiều năng lượng hơn để giữ kết nối đến D đáng tin cậy khi 
tăng α. Tuy nhiên, càng nhiều thời gian cho thu thập năng lượng thì càng ít thời gian cho 
Phân tích xác suất dừng của việc lựa chọn UAV thu thập năng lượng 
41 
truyền tin, làm cho dung lượng kênh truyền thấp hơn trong giai đoạn 3 mà sau cùng, sẽ làm 
tăng OP. Do đó, khi hệ số chia thời gian lớn hơn một giá trị nhất định (ví dụ: α = 0,7 với M = 10 
như trong Hình 3), OP tăng khi tăng α. Như vậy, α nên được tối ưu để đạt được truyền thông 
tin cậy. Hơn nữa, độ tin cậy truyền tin được cải thiện bằng cách triển khai nhiều UAV hơn, 
cho thấy hiệu quả của việc lựa chọn UAV. 
Bên cạnh hệ số chia thời gian, hiệu suất chuyển đổi năng lượng là một yếu tố quan 
trọng khác ảnh hưởng đến lượng năng lượng thu thập, mà cuối cùng sẽ ảnh hưởng đến hiệu 
năng hệ thống. Hình 4 biểu thị OP theo cả α và η với các thông số tương tự như Hình 3 ngoại 
trừ M = 10. Kết quả cho thấy rằng cho trước α thì η càng lớn sẽ cho OP càng nhỏ. Điều này 
hợp lý bởi vì tăng η giúp UAV thu thập được nhiều năng lượng hơn và do đó, truyền tín hiệu 
với công suất lớn hơn và cho OP thấp hơn. Để dễ quan sát ảnh hưởng của cả α và η lên OP, 
chúng ta tìm vùng trên mặt phẳng (η, α) mà OP nhỏ hơn một mức nhất định cho độ tin cậy 
kết nối chấp nhận được. Hình 4 biểu thị vùng này trong đó OP nhỏ hơn 20%. Ta thấy rằng 
hiệu suất chuyển đổi năng lượng càng thấp thì càng cần nhiều thời gian để thu thập năng 
lượng. Việc mà η tỷ lệ nghịch với OP là hợp lý để giữ cho lượng năng lượng thu thập được 
trên một mức nhất định (nghĩa là, tích của α và η là hằng số cho lượng năng lượng thu thập 
không đổi: 
2
i iR S SR
EH TP h = ). 
Hình 4. Xác suất dừng theo α và η 
5. KẾT LUẬN 
Nghiên cứu này đã mô tả một hệ thống truyền thông chuyển tiếp được hỗ trợ bởi các 
UAV trong đó chỉ có một UAV trong số nhiều UAV được chọn làm thiết bị chuyển tiếp. Tất 
cả các UAV đều có khả năng thu thập năng lượng từ tín hiệu tần số vô tuyến. Hiệu năng của 
hệ thống đã được phân tích theo xác suất dừng của thiết bị đích thông qua biểu thức dạng 
tường minh chính xác được đề xuất. Phân tích được xác minh bằng mô phỏng Monte-Carlo. 
Nhiều kết quả cho thấy hiệu quả của việc lựa chọn UAV trong việc giữ kết nối tin cậy qua 
khoảng cách lớn. Ngoài ra, các kết quả đã chứng minh rằng hệ số phân chia thời gian cho quá 
trình thu thập năng lượng có thể được tối ưu hóa để đạt được hiệu năng hệ thống tốt nhất. 
Một trong các vấn đề thu hút nhiều sự quan tâm về hệ thống truyền thông chuyển tiếp 
được hỗ trợ bởi các UAV là bảo mật thông tin vì các UAV có thể là các thiết bị nghe lén nhằm 
trích xuất thông tin mật của thiết bị nguồn. Do đó, hướng phát triển của bài báo này là nghiên 
cứu các giải pháp bảo mật cho hệ thống truyền thông chuyển tiếp được hỗ trợ bởi các UAV. 
Hồ Văn Khương 
42 
TÀI LIỆU THAM KHẢO 
1. Santos N.P., Lobo V., and Bernardino A. - Directional statistics for 3D model-based 
UAV tracking, IEEE Access 8 (2020) 33884-33897. 
2. Mozaffari M., Saad W., Bennis M., Nam Y., and Debbah M. - A tutorial on UAVs for 
wireless networks: Applications, challenges, and open problems, IEEE Communications 
Surveys & Tutorials 21 (3) (2019) 2334-2360. 
3. Ji L., Chen J., and Feng Z. - Spectrum allocation and performance analysis for 
backhauling of UAV assisted cellular network, China Communications 16 (8) (2019) 
83-92. 
4. Sobouti M.J., Rahimi Z., Mohajerzadeh A.H., Seno S.A.H., Ghanbari R., Marquez-
Barja J.M., and Ahmadi H. - Efficient deployment of small cell base stations mounted 
on unmanned aerial vehicles for the internet of things infrastructure, IEEE Sensors 
Journal 20 (13) (2020) 7460-7471. 
5. Abdelhady A.M., Amin O., Shihada B., Alouini M. - Spectral efficiency and energy 
harvesting in multi-cell SLIPT systems, IEEE Transactions on Wireless Communications 
19 (5) (2020) 3304-3318. 
6. Abualhaol I.Y., Matalgah M.M. - Outage probability analysis in a cooperative UAVs 
network over nakagami-m fading channels, IEEE Vehicular Technology Conference, 
Montreal, Que. (2006) 1-4. 
7. Chen Y., Zhao N., Ding Z., and Alouini M. - Multiple UAVs as relays: Multi-hop single 
link versus multiple dual-hop links, IEEE Transactions on Wireless Communications 17 
(9) (2018) 6348-6359. 
8. Hanna S., Krijestorac E., Yan H. and Cabric D. - UAV swarms as amplify-and-
forward MIMO relays, 20198 IEEE 20th International Workshop on Signal Processing 
Advances in Wireless Communications (SPAWC), Cannes, France (2019) 1-5. 
9. Zwillinger D., Moll V., Gradshteyn I. and I. Ryzhik - Definite Integrals of elementary 
functions, in: Table of Integrals, Series, and Products (8th Edn) (Ed. Zwillinger D.), 
Boston: Academic Press (2015) 249-519. 
ABSTRACT 
OUTAGE PROBABILITY ANALYSIS OF ENERGY HARVESTING UAV SELECTION 
Ho Van Khuong 
Ho Chi Minh City University of Technology, VNU-HCM 
Email: hvkhuong@hcmut.edu.vn 
This paper analyzes reliability performance of an UAV (Unmanned Aerial Vehicles)-
aided relaying system where only one UAV among multiple UAVs, all capable of harvesting 
energy from radio frequency signals, is selected as a relay. To this end, a precise closed-form 
outage probability formula is first derived. Then, Monte-Carlo simulations are conducted to 
validate the proposed formula. Finally, various results are provided to illustrate the impact of 
key operation parameters on the outage performance of the UAV selection. 
Keywords: Outage probability, UAV, energy harvesting, relaying.