Phân lớp hiệu quả tập dữ liệu lớn với giải thuật giảm gradient ngẫu nhiên

2) trong đó m là số lượng phần tử được dùng để huấn luyện. Điều này làm cho giải thuật SVM không phù 
hợp với dữ liệu lớn. 
B. Giải thuật giảm gradient (GD) 
 Một cài đặt cho giải thuật SVM dựa trên phương pháp giảm gradient (Gradient Descent – GD, tham khảo [Boyd 
& Vandenberghe, 2004]), có độ phức tạp tuyến tính với số phần tử dữ liệu. Để đơn giản, người ta không xét độ lệch b ở 
đây. Các ràng buộc trong bài toán quy hoạch toàn phương (1) có thể được viết lại như sau: 
540 PHÂN LỚP TẬP DỮ LIỆU LỚN VỚI GIẢI THUẬT SVM-SGD 
 zi ≥ 1 - yi(w.xi) (3) 
 zi ≥ 0 (i=1,m) (4) 
 Các ràng buộc (3), (4) có thể được viết ngắn gọn như (5): 
 zi = max{0, 1 - yi(w.xi)} (5) 
 Bằng cách thay thế zi từ (5) vào hàm mục tiêu của (1), việc tìm siêu phẳng tối ưu của SVM có thể được viết lại 
như vấn đề (6): 
 m
 min (w, x, y) = (λ/2) ||w||2 +(1/m) (6) 
 max{0,1 yi (w.xi )}
 i 1
 Phương pháp giảm gradient (GD) thực hiện tối ưu vấn đề (6) bằng cách cập nhật w tại lần lặp thứ (t+1) dựa trên 
wΨ(wt) (gradient của hàm theo w của lần lặp thứ t), với tốc độ học t, như trong (7): 
 m
 w = w - ( /m) (7) 
 t+1 t t w (wt , xi , yi )
 i 1
 [Cotter et al., 2011] cũng đề xuất một cách cài đặt dựa trên phương pháp giảm gradient sử dụng tập con ngẫu 
nhiên để cập nhật w tạo mỗi lần lặp, tăng tốc độ hội tụ đến lời giải nhanh hơn phương pháp giảm gradient. 
 Mặc dù mỗi lần lặp, phương pháp giảm gradient cập nhật w rất đơn giản, nhưng tốc độ hội tụ của giải thuật 
giảm gradient chậm so với phương pháp lặp Newton [Boyd & Vandenberghe, 2004]. 
 Đại lượng lỗi zi = max{0, 1 - yi(w.xi)} trong vấn đề tối ưu (6) của máy học SVM thường được gọi là hàm lỗi 
hinge loss được viết dưới dạng: 
 Lhinge(x) = max{0, 1 - x} (8) 
 Chú ý rằng hàm hinge loss không khả vi tại yi(w.xi)=1. Điều này ảnh hưởng đến tốc độ hội tụ của giải thuật 
giảm gradient. 
 Để khắc phục được vấn đề này, các giải pháp phổ biến có thể là: sử dụng phương pháp giảm subgradient hoặc 
thay thế hàm lỗi xấp xỉ khả vi của hinge loss. 
 Giải thuật giảm gradient ngẫu nhiên (SGD) của [Bottou & Boussquet, 2008], [Shalev-Shwartz et al., 2007] thực 
hiện đơn giản bước cập nhật wt+1 dựa trên subgradient chỉ sử dụng một phần tử ngẫu nhiên (xt, yt) tại mỗi lần lặp: 
 wt+1 = wt - tw(wt, xt, yt) (9) 
 [Bottou & Bousquet, 2008], [Shalev-Shwartz et al., 2007] chứng minh rằng phương pháp giảm gradient ngẫu 
nhiên có độ phức tạp tuyến tính với số phần tử dữ liệu. 
C. Hàm xấp xỉ khả vi của hinge loss 
 Chúng tôi đề xuất thay thế hàm hinge loss không khả vi bằng các hàm xấp xỉ khả vi để có thể sử dụng trong giải 
thuật giảm gradient cho vấn đề phân lớp của SVM. Trong nghiên cứu của [Rennie, 2004], hàm xấp xỉ khả vi của hinge 
loss cần có tính chất quan trọng tương tự của hàm hinge loss của mô hình SVM để đảm được lề (margin) bằng 1. Nghĩa 
là hàm xấp xỉ bằng 0 khi x ≥ 1; có hệ số gốc là hằng số âm khi x ≤ 0; phải trơn vị trí chuyển từ hệ số gốc bằng 0 sang 
hệ số gốc âm có chuyển khi 0 < x < 1. 
 Dựa trên các yêu cầu trên, chúng tôi đề xuất hàm xấp xỉ khả vi alpha-smoothing của hinge loss, sử dụng tham số 
α (là số nguyên lớn hơn 1), được định nghĩa như sau: 
 1
 x if (x 0)
 x 1 (10) 
 L (x) x if (0 x 1)
 0 if (x 1)
 Ngoài ra, hàm logistic loss (logit) là hàm xấp xỉ khả vi khác của hinge loss cũng thỏa mãn các yêu cầu trên, nên 
có thể được sử dụng để thay thế cho hinge loss. Hàm logit có dạng như sau: 
Đỗ Thanh Nghị, Phạm Thế Phi 541 
 Llogit(x) = log(1 + e-x) (11) 
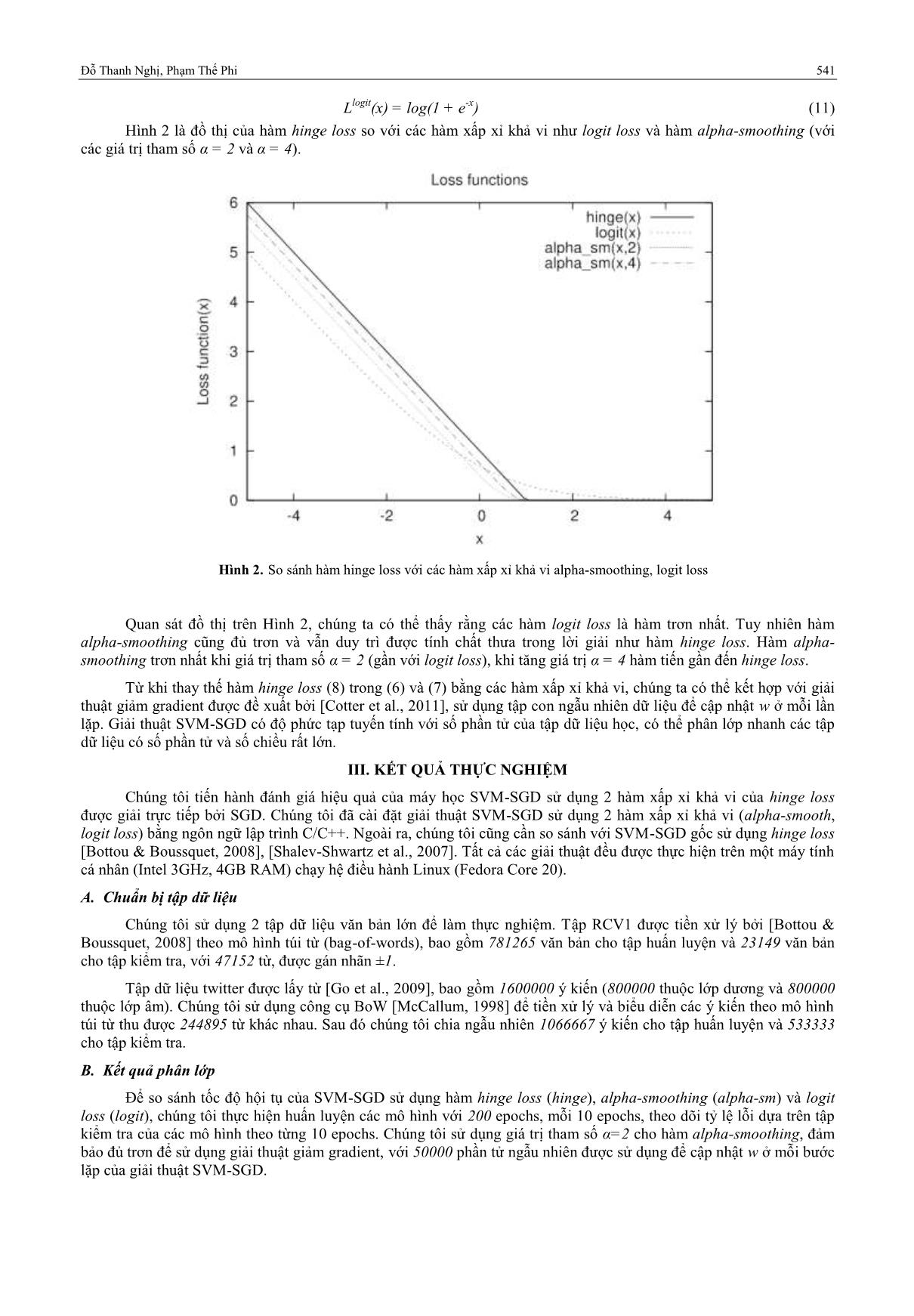
 Hình 2 là đồ thị của hàm hinge loss so với các hàm xấp xỉ khả vi như logit loss và hàm alpha-smoothing (với 
các giá trị tham số α = 2 và α = 4). 
 Hình 2. So sánh hàm hinge loss với các hàm xấp xỉ khả vi alpha-smoothing, logit loss 
 Quan sát đồ thị trên Hình 2, chúng ta có thể thấy rằng các hàm logit loss là hàm trơn nhất. Tuy nhiên hàm 
alpha-smoothing cũng đủ trơn và vẫn duy trì được tính chất thưa trong lời giải như hàm hinge loss. Hàm alpha-
smoothing trơn nhất khi giá trị tham số α = 2 (gần với logit loss), khi tăng giá trị α = 4 hàm tiến gần đến hinge loss. 
 Từ khi thay thế hàm hinge loss (8) trong (6) và (7) bằng các hàm xấp xỉ khả vi, chúng ta có thể kết hợp với giải 
thuật giảm gradient được đề xuất bởi [Cotter et al., 2011], sử dụng tập con ngẫu nhiên dữ liệu để cập nhật w ở mỗi lần 
lặp. Giải thuật SVM-SGD có độ phức tạp tuyến tính với số phần tử của tập dữ liệu học, có thể phân lớp nhanh các tập 
dữ liệu có số phần tử và số chiều rất lớn. 
 III. KẾT QUẢ THỰC NGHIỆM 
 Chúng tôi tiến hành đánh giá hiệu quả của máy học SVM-SGD sử dụng 2 hàm xấp xỉ khả vi của hinge loss 
được giải trực tiếp bởi SGD. Chúng tôi đã cài đặt giải thuật SVM-SGD sử dụng 2 hàm xấp xỉ khả vi (alpha-smooth, 
logit loss) bằng ngôn ngữ lập trình C/C++. Ngoài ra, chúng tôi cũng cần so sánh với SVM-SGD gốc sử dụng hinge loss 
[Bottou & Boussquet, 2008], [Shalev-Shwartz et al., 2007]. Tất cả các giải thuật đều được thực hiện trên một máy tính 
cá nhân (Intel 3GHz, 4GB RAM) chạy hệ điều hành Linux (Fedora Core 20). 
A. Chuẩn bị tập dữ liệu 
 Chúng tôi sử dụng 2 tập dữ liệu văn bản lớn để làm thực nghiệm. Tập RCV1 được tiền xử lý bởi [Bottou & 
Boussquet, 2008] theo mô hình túi từ (bag-of-words), bao gồm 781265 văn bản cho tập huấn luyện và 23149 văn bản 
cho tập kiểm tra, với 47152 từ, được gán nhãn ±1. 
 Tập dữ liệu twitter được lấy từ [Go et al., 2009], bao gồm 1600000 ý kiến (800000 thuộc lớp dương và 800000 
thuộc lớp âm). Chúng tôi sử dụng công cụ BoW [McCallum, 1998] để tiền xử lý và biểu diễn các ý kiến theo mô hình 
túi từ thu được 244895 từ khác nhau. Sau đó chúng tôi chia ngẫu nhiên 1066667 ý kiến cho tập huấn luyện và 533333 
cho tập kiểm tra. 
B. Kết quả phân lớp 
 Để so sánh tốc độ hội tụ của SVM-SGD sử dụng hàm hinge loss (hinge), alpha-smoothing (alpha-sm) và logit 
loss (logit), chúng tôi thực hiện huấn luyện các mô hình với 200 epochs, mỗi 10 epochs, theo dõi tỷ lệ lỗi dựa trên tập 
kiểm tra của các mô hình theo từng 10 epochs. Chúng tôi sử dụng giá trị tham số α=2 cho hàm alpha-smoothing, đảm 
bảo đủ trơn để sử dụng giải thuật giảm gradient, với 50000 phần tử ngẫu nhiên được sử dụng để cập nhật w ở mỗi bước 
lặp của giải thuật SVM-SGD. 
542 PHÂN LỚP TẬP DỮ LIỆU LỚN VỚI GIẢI THUẬT SVM-SGD 
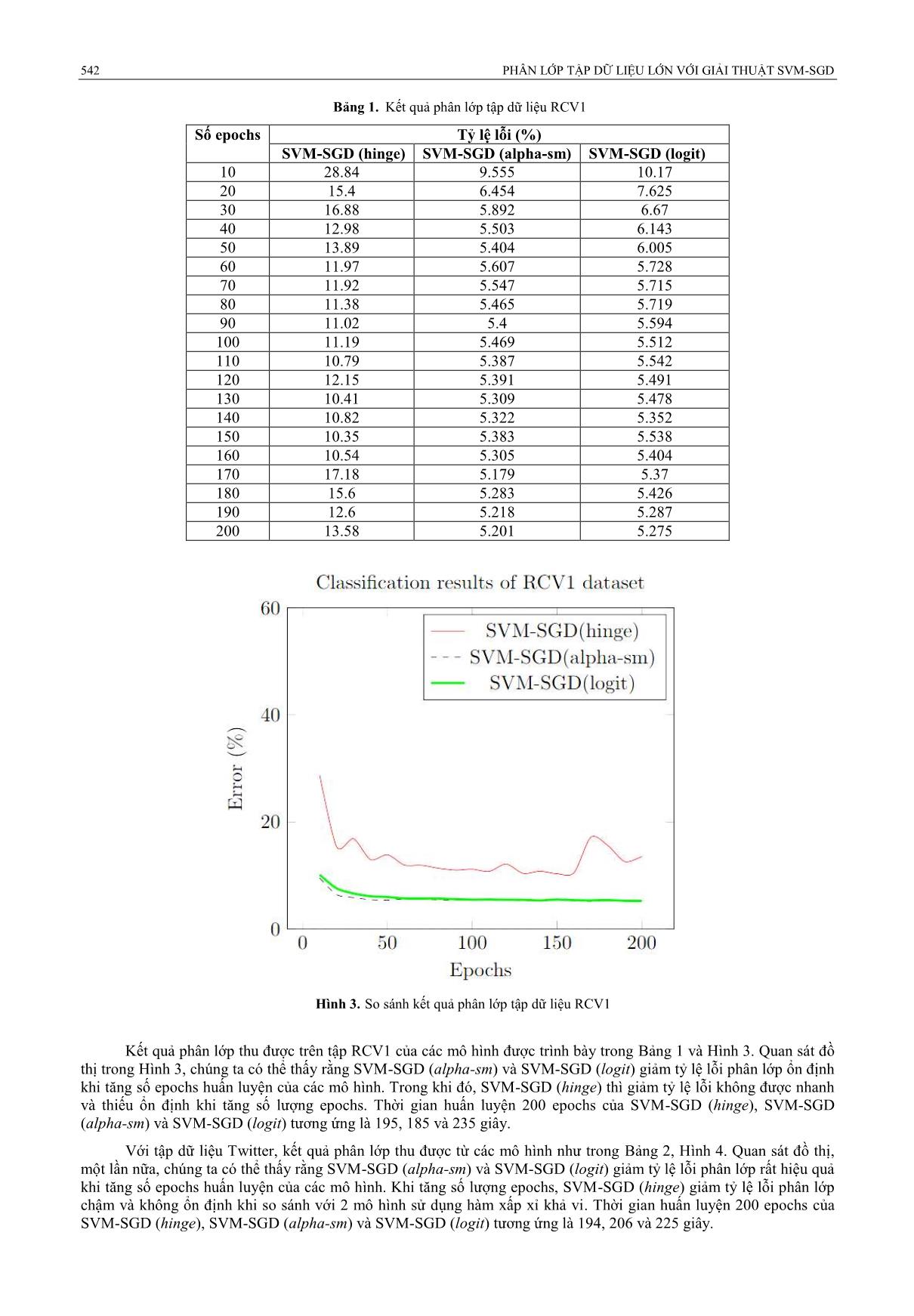
 Bảng 1. Kết quả phân lớp tập dữ liệu RCV1 
 Số epochs Tỷ lệ lỗi (%) 
 SVM-SGD (hinge) SVM-SGD (alpha-sm) SVM-SGD (logit) 
 10 28.84 9.555 10.17 
 20 15.4 6.454 7.625 
 30 16.88 5.892 6.67 
 40 12.98 5.503 6.143 
 50 13.89 5.404 6.005 
 60 11.97 5.607 5.728 
 70 11.92 5.547 5.715 
 80 11.38 5.465 5.719 
 90 11.02 5.4 5.594 
 100 11.19 5.469 5.512 
 110 10.79 5.387 5.542 
 120 12.15 5.391 5.491 
 130 10.41 5.309 5.478 
 140 10.82 5.322 5.352 
 150 10.35 5.383 5.538 
 160 10.54 5.305 5.404 
 170 17.18 5.179 5.37 
 180 15.6 5.283 5.426 
 190 12.6 5.218 5.287 
 200 13.58 5.201 5.275 
 Hình 3. So sánh kết quả phân lớp tập dữ liệu RCV1 
 Kết quả phân lớp thu được trên tập RCV1 của các mô hình được trình bày trong Bảng 1 và Hình 3. Quan sát đồ 
thị trong Hình 3, chúng ta có thể thấy rằng SVM-SGD (alpha-sm) và SVM-SGD (logit) giảm tỷ lệ lỗi phân lớp ổn định 
khi tăng số epochs huấn luyện của các mô hình. Trong khi đó, SVM-SGD (hinge) thì giảm tỷ lệ lỗi không được nhanh 
và thiếu ổn định khi tăng số lượng epochs. Thời gian huấn luyện 200 epochs của SVM-SGD (hinge), SVM-SGD 
(alpha-sm) và SVM-SGD (logit) tương ứng là 195, 185 và 235 giây. 
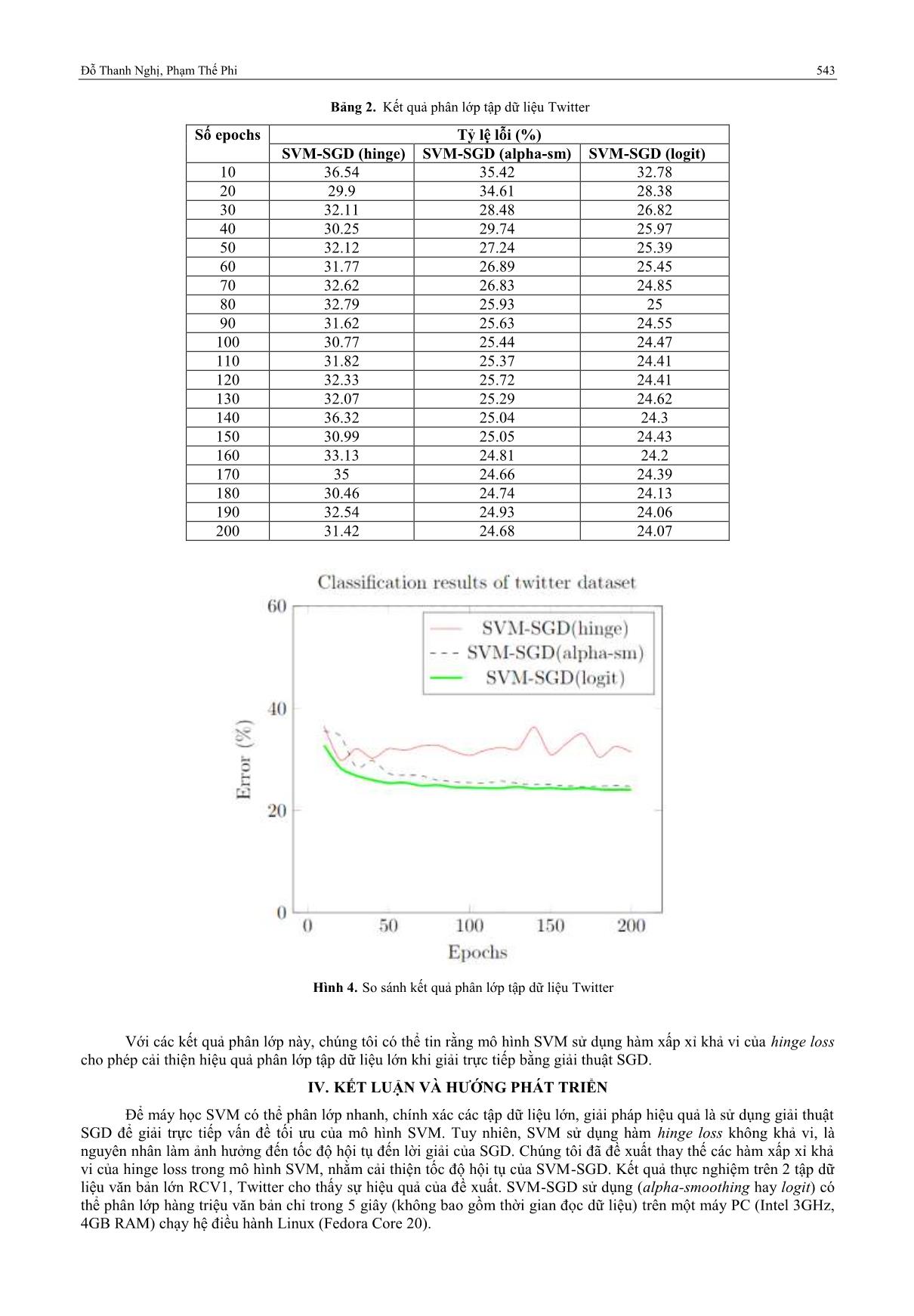
 Với tập dữ liệu Twitter, kết quả phân lớp thu được từ các mô hình như trong Bảng 2, Hình 4. Quan sát đồ thị, 
một lần nữa, chúng ta có thể thấy rằng SVM-SGD (alpha-sm) và SVM-SGD (logit) giảm tỷ lệ lỗi phân lớp rất hiệu quả 
khi tăng số epochs huấn luyện của các mô hình. Khi tăng số lượng epochs, SVM-SGD (hinge) giảm tỷ lệ lỗi phân lớp 
chậm và không ổn định khi so sánh với 2 mô hình sử dụng hàm xấp xỉ khả vi. Thời gian huấn luyện 200 epochs của 
SVM-SGD (hinge), SVM-SGD (alpha-sm) và SVM-SGD (logit) tương ứng là 194, 206 và 225 giây. 
Đỗ Thanh Nghị, Phạm Thế Phi 543 
 Bảng 2. Kết quả phân lớp tập dữ liệu Twitter 
 Số epochs Tỷ lệ lỗi (%) 
 SVM-SGD (hinge) SVM-SGD (alpha-sm) SVM-SGD (logit) 
 10 36.54 35.42 32.78 
 20 29.9 34.61 28.38 
 30 32.11 28.48 26.82 
 40 30.25 29.74 25.97 
 50 32.12 27.24 25.39 
 60 31.77 26.89 25.45 
 70 32.62 26.83 24.85 
 80 32.79 25.93 25 
 90 31.62 25.63 24.55 
 100 30.77 25.44 24.47 
 110 31.82 25.37 24.41 
 120 32.33 25.72 24.41 
 130 32.07 25.29 24.62 
 140 36.32 25.04 24.3 
 150 30.99 25.05 24.43 
 160 33.13 24.81 24.2 
 170 35 24.66 24.39 
 180 30.46 24.74 24.13 
 190 32.54 24.93 24.06 
 200 31.42 24.68 24.07 
 Hình 4. So sánh kết quả phân lớp tập dữ liệu Twitter 
 Với các kết quả phân lớp này, chúng tôi có thể tin rằng mô hình SVM sử dụng hàm xấp xỉ khả vi của hinge loss 
cho phép cải thiện hiệu quả phân lớp tập dữ liệu lớn khi giải trực tiếp bằng giải thuật SGD. 
 IV. KẾT LUẬN VÀ HƯỚNG PHÁT TRIỂN 
 Để máy học SVM có thể phân lớp nhanh, chính xác các tập dữ liệu lớn, giải pháp hiệu quả là sử dụng giải thuật 
SGD để giải trực tiếp vấn đề tối ưu của mô hình SVM. Tuy nhiên, SVM sử dụng hàm hinge loss không khả vi, là 
nguyên nhân làm ảnh hưởng đến tốc độ hội tụ đến lời giải của SGD. Chúng tôi đã đề xuất thay thế các hàm xấp xỉ khả 
vi của hinge loss trong mô hình SVM, nhằm cải thiện tốc độ hội tụ của SVM-SGD. Kết quả thực nghiệm trên 2 tập dữ 
liệu văn bản lớn RCV1, Twitter cho thấy sự hiệu quả của đề xuất. SVM-SGD sử dụng (alpha-smoothing hay logit) có 
thể phân lớp hàng triệu văn bản chỉ trong 5 giây (không bao gồm thời gian đọc dữ liệu) trên một máy PC (Intel 3GHz, 
4GB RAM) chạy hệ điều hành Linux (Fedora Core 20). 
544 PHÂN LỚP TẬP DỮ LIỆU LỚN VỚI GIẢI THUẬT SVM-SGD 
 Trong tương lai, chúng tôi tiếp tục nghiên cứu các hàm xấp xỉ khả vi khác của hinge loss. Chúng tôi sẽ phát 
triển giải thuật SVM-SGD song song cho phép tăng tốc quá trình thực thi trên máy tính có nhiều bộ xử lý, nhóm hay 
lưới máy tính. 
 TÀI LIỆU THAM KHẢO 
[1] Boser, B., Guyon, I., Vapnik, V., “An training algorithm for optimal margin classifiers”, In proceedings of 5th ACM Annual 
 Workshop on Computational Learning Theory, pp.144-152, 1992. 
[2] Bottou, L., Bousquet, O.: “The tradeoffs of large scale learning”, In Advances in Neural Information Processing Systems 
 (20):161-168, 2008. 
[3] Boyd, S. and Vandenberghe, L.: “Convex Optimization”, Cambridge University Press, 2004. 
[4] Breiman, L., “Arcing classifiers”, The Annals of Statistics, vol. 26, no. 3, pp.801-849, 1998. 
[5] Chang, C. C., Lin, C. J., “LIBSVM: a library for support vector machines”, ACM Transactions on Intelligent Systems and 
 Technology, vol. 2, no. 27, pp.1-27, 2011  
[6] Cotter, A., Shamir, O., Srebro, N., and Sridharan, K.: “Better Mini-Batch Algorithms via Accelerated Gradient Methods”, 
 NIPS, pp. 1647-1655, 2011. 
[7] Cristianini, N., Shawe-Taylor, J., “An Introduction to Support Vector Machines: And Other Kernel-based Learning Methods”, 
 Cambridge University Press, New York, NY, USA, 2000. 
[8] Do, T.N., “Parallel multiclass stochastic gradient descent algorithms for classifying million images with very-high-dimensional 
 signatures into thousands classes”, Vietnam J. Computer Science, vol. 1, no. 2, pp.107-115, 2014. 
[9] Do, T.N., Nguyen, V.H., Poulet, F., “Speedup SVM algorithm for massive classification tasks”, In Proceedings of ADMA, 
 pp.147-157, 2008. 
[10] Do, T.N., Fekete, J.D., “Large scale classification with support vector machine algorithms. In The Sixth International 
 Conference on Machine Learning and Applications, ICMLA 2007, Cincinnati, Ohio, USA, pp.7-12, 2007. 
[11] Do, T.N., Poulet, F., “Classifying one billion data with a new distributed svm algorithm”, In proceedings of 4th IEEE Intl. 
 Conf. on Computer Science, Research, Innovation and Vision for the Future, IEEE Press, pp.59-66, 2006. 
[12] Do, T.N., Poulet, F., “Mining very large datasets with svm and visualization”, In proceedings of 7th Intl. Conf. on Entreprise 
 Information Systems, pp.127-134, 2005. 
[13] Freund, Y., Schapire, R., “A short introduction to boosting”, Journal of Japanese Society for Artificial Intelligence, vol. 14, no. 
 5, pp.771-780, 1999. 
[14] Go, A., Bhayani, R., Huang, L.: “Twitter sentiment”, May 12th 2014 (accessed date),  
[15] Guyon, I., Web page on svm applications, 1999,  
[16] Liu H., Syed, N. and K. Sung.: “Incremental learning with support vector machines”, ACM SIGKDD, 1999. 
[17] McCallum, A.: “Bow: A Toolkit for Statistical Language Modeling, Text Retrieval, Classification and Clustering”, 1998. 
[18] Mangasarian O.L.: “Mathematical Programming for Support Vector Machines”, INRIA Rocquencourt, France July 17, 2001. 
[19] Osuna, E., Freund, R., Girosi, F., “An improved training algorithm for support vector machines”, Neural Networks for Signal 
 Processing VII, J. Principe, L. Gile, N. Morgan, and E. Wilson Eds, pp.276-285, 1997. 
[20] Platt J.: Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines, Microsoft Research 
 Technical Report MSR-TR-98-14, 1998. 
[21] Poulet, F., Do, T.N., “Mining very large datasets with support vector machine algorithms”, Enterprise Information Systems V, 
 O. Camp, J. Filipe, S. Hammoudi and M. Piattini Eds., pp.177-184, 2004. 
[22] Rennie, J.D.M.: “Derivation of the f-measure”,  (February 2004). 
[23] Shalev-Shwartz, S., Singer, Y., Srebro, N., “Pegasos: Primal estimated sub-gradient solver for svm”, In Proceedings of the 
 Twenty-Fourth International Conference Machine Learning, ACM, pp.807-814, 2007. 
[24] Suykens, J., Vandewalle, J. “Least squares support vector machines classifiers”, Neural Processing Letters, vol. 9, no. 3, 
 pp.293–300, 1999. 
[25] Tong, S., Koller, D., “Support vector machine active learning with applications to text classification”, In proceedings of the 
 17th Intl. Conf. on Machine Learning, ACM, pp. 999-1006, 2000. 
[26] Vapnik, V.: “The Nature of Statistical Learning Theory”, Springer-Verlag, 1995. 
[27] Wu X. and Kumar V.: “Top 10 Algorithms in Data Mining”, Chapman & Hall/CRC, 2009. 
 EFFICIENTLY CLASSIFYING VERY LARGE DATASETS WITH 
 STOCHASTIC GRADIENT DESCENT 
 Thanh Nghi Do, The Phi Pham 
ABSTRACT— In this paper, we present the support vector machines algorithm using the stochastic gradient descent for classifying 
very large datasets. To reach to the sparsity in the solution, the support vector machines algorithm uses the hinge loss in 
classification tasks. Thus, the direct optimization using the stochastic gradient descent is difficult due to the differentiation of the 
hinge loss. Our proposal is to substitute the hinge loss used in the problem formula of the support vector machines algorithm by the 
smooth ones to improve the convergence rate of the stochastic gradient descent. The numerical test results on two large textual 
datasets (RCV1, twitter) show that our proposal is more efficient than the usual hinge loss.