Partition fuzzy domain with multi - granularity representation of data based on hedge algebra approach

 = 0.38, P(class = 3) = 0.01〉). This system,
according to the authors, has a high rate of classification and interpretability. In summary,
the use of multi-granular representations gives us a high degree of general and well-defined
knowledge that improves the performance of the method.
For fuzzy set theory (according to L.Zadeh), one of the limitations of methods of using
multi-granular representations is that sometimes the selection of nonlinear functions is not
easy since there are few reasons for defining membership functions of different levels and
the relationship between them. Mostly, this determination is conducted only by experience,
and in the above example we can also feel it. Simultaneously, carrying out calculations at
different levels of data will entail complexity that costs much more in terms of time and
memory. Even in recent studies [4], in the fuzzy rule-building application of the regression
problem, the authors also use only single granularity presentation approach. In particular,
using the evolutionary algorithm to construct the fuzzy rule set on the basis of optimizing
fuzzy partition MF sets determines the properties of both the fuzzy domain division for each
attribute and the other criteria mentioned above. Although the algorithm (performs) in [4]
is better than existing ones as the number of fuzzy sets used to divide the domain attribute
is not pre-predetermining but about semantics, it still does not allow the construction of
different general and detailed rules in the same fuzzy rule system. On the contrary, with the
hedge algebra, it is easy to identify fuzzy measurements at different levels of multi-granularity
representation as it lies at the construction of the hedge algebra. In the hedge algebra’s
theory, it is only necessary to determine once the fuzzy measure values of the generating
elements and the hedges, then we can determine the fuzzy range of all the elements based
on the determined calculating formulas no matter how long this element is (i.e., how much
this element is in the multi-granularity representation system). Decentralization, one of the
main ways that GrC uses, is the way the hedge algebra is built. According to the theory of
the hedge algebra, each of the element x of length k can be subdivided into elements hix
(where hi is the hedge of hedge algebra that is being considered) with length k + 1. It can
be said that the hedge algebra is a very suitable tool for multi-granularity computing. The
example presented later will further clarify that.
3.3. MFs Codification and Initial Gene Pool
In this paper, we use structured HA as follows:
AT = (X,G, H,≤), G = {C− = {Low} ∪ C+ = {High}},
H = {H− = {Little} ∪H+ = {V ery}}.
PARTITION FUZZY DOMAIN WITH MULTI-GRANULARITY REPRESENTATION ... 69
1
1
2-Level
02 V C− LC− LC+ V C+ 12
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
1
1-Level
01 C− C+ 11
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
1
0-Level
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
00 W 10
Figure 4. Building MF based on Multi-granular representation for an attribute
α = µ (Little) = 1− µ (V ery), β = 1− α, w = fm (Low) = 1− fm (High) .
We performed a chromosome, a real number array size n× 2 (where n is the number of
items, 2 corresponds to the parameter α and w in each HA): {(α1, w1) , (α2, w2) , ..., (αn, wn)}.
For each pair (αi, wi) are parameters of a HA
Initialize population consisting of N chromosomes: based on the experience of the value
α and w will receive a random value in the interval [0.2 to 0.8].
Example: with α = 0.5, w = 0.5, MFs is built as shown in Figure 4. Similarly, each
attribute in the database will be built the MFs, as shown in Figure 4.
4. PROPOSED MINING ALGORITHM
In this section, our approach used partition fuzzy domain with multi-granularity repre-
sentation of data, a proposed algorithm for mining MFs and association rules is described in
detail.
Input: Transaction database with T quantities, n-item set (each item has m predefined
linguistic terms), support threshold Min Support, confidence threshold Min Confidence,
population size N.
Output: Set of association rules with its associated set of MFs.
Phase 1: Learning the MFs.
In this paper, we use a multi-granularity approach. Each attribute in the database will
be built by MFs, as shown in Figure 4. The MFs is a string encryption as described in
Section 3.3. Using the algorithm in [15], we obtain a set of MFs to use for Phase 2.
Phase 2: Mining fuzzy association rules.
The set of the best MFs is then applied in mining fuzzy association rules from the given
transaction database using the algorithm proposed in [13].
70 TRAN THAI SON, NGUYEN TUAN ANH
5. EXPERIMENTAL RESULTS
In this part, we present the experimental results of the proposed method for a particular
database. The source of the data is taken from the FAM95 database, conducted by the
Bureau of Statistics for the Bureau of Labor Statistics in 1995. We selected 10 attribute
numbers that include: age of the head of the family, number of persons in the family, number
of children, hours head worked last week, head of personal income, family income, taxable
income for head, federal tax for head, final sampling weight for weight and March supplement
income and tax [1, 6, 9].
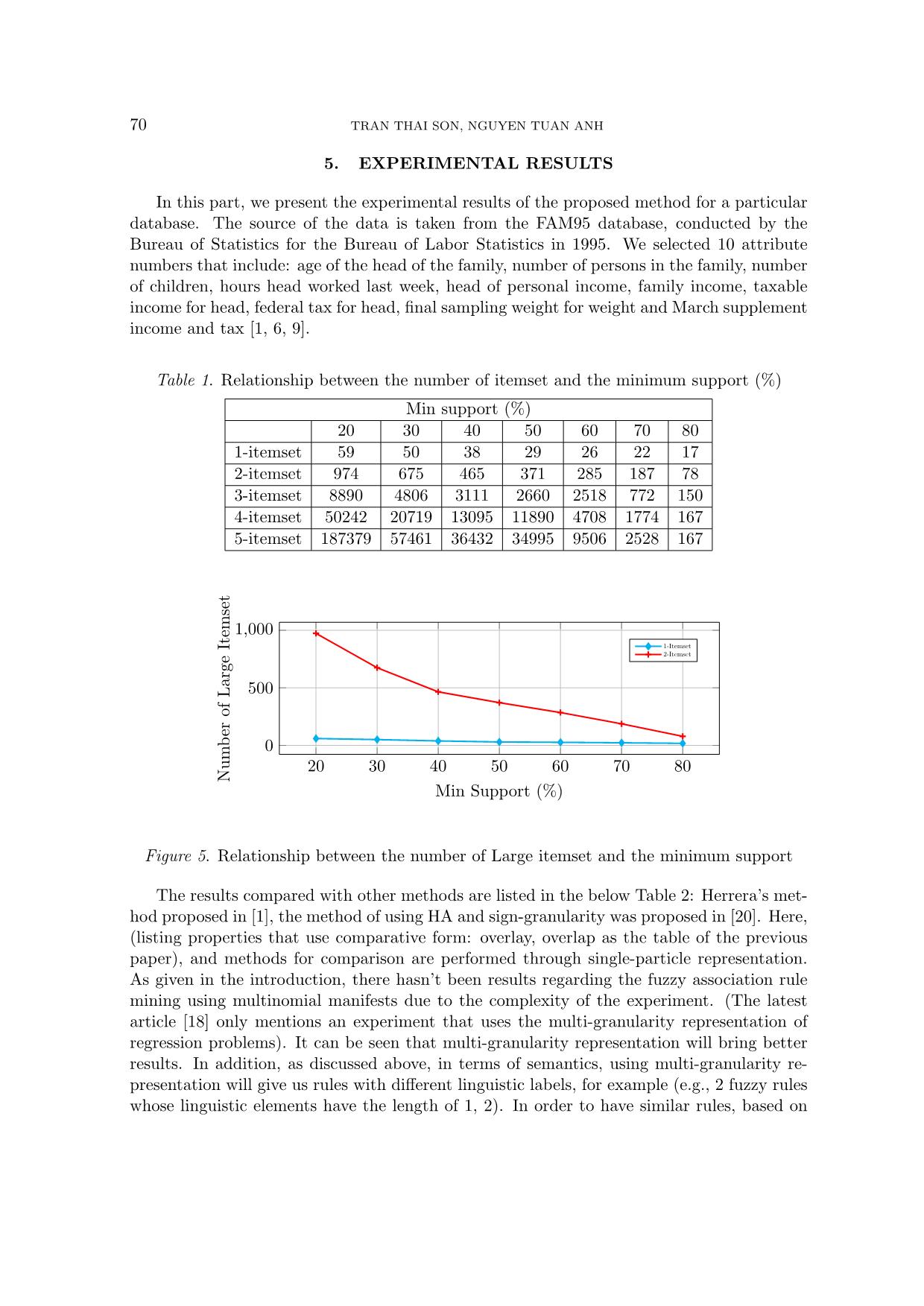
Table 1. Relationship between the number of itemset and the minimum support (%)
Min support (%)
20 30 40 50 60 70 80
1-itemset 59 50 38 29 26 22 17
2-itemset 974 675 465 371 285 187 78
3-itemset 8890 4806 3111 2660 2518 772 150
4-itemset 50242 20719 13095 11890 4708 1774 167
5-itemset 187379 57461 36432 34995 9506 2528 167
20 30 40 50 60 70 80
0
500
1,000
Min Support (%)
N
u
m
b
er
o
f
L
a
rg
e
It
em
se
t
1-Itemset
2-Itemset
Figure 5. Relationship between the number of Large itemset and the minimum support
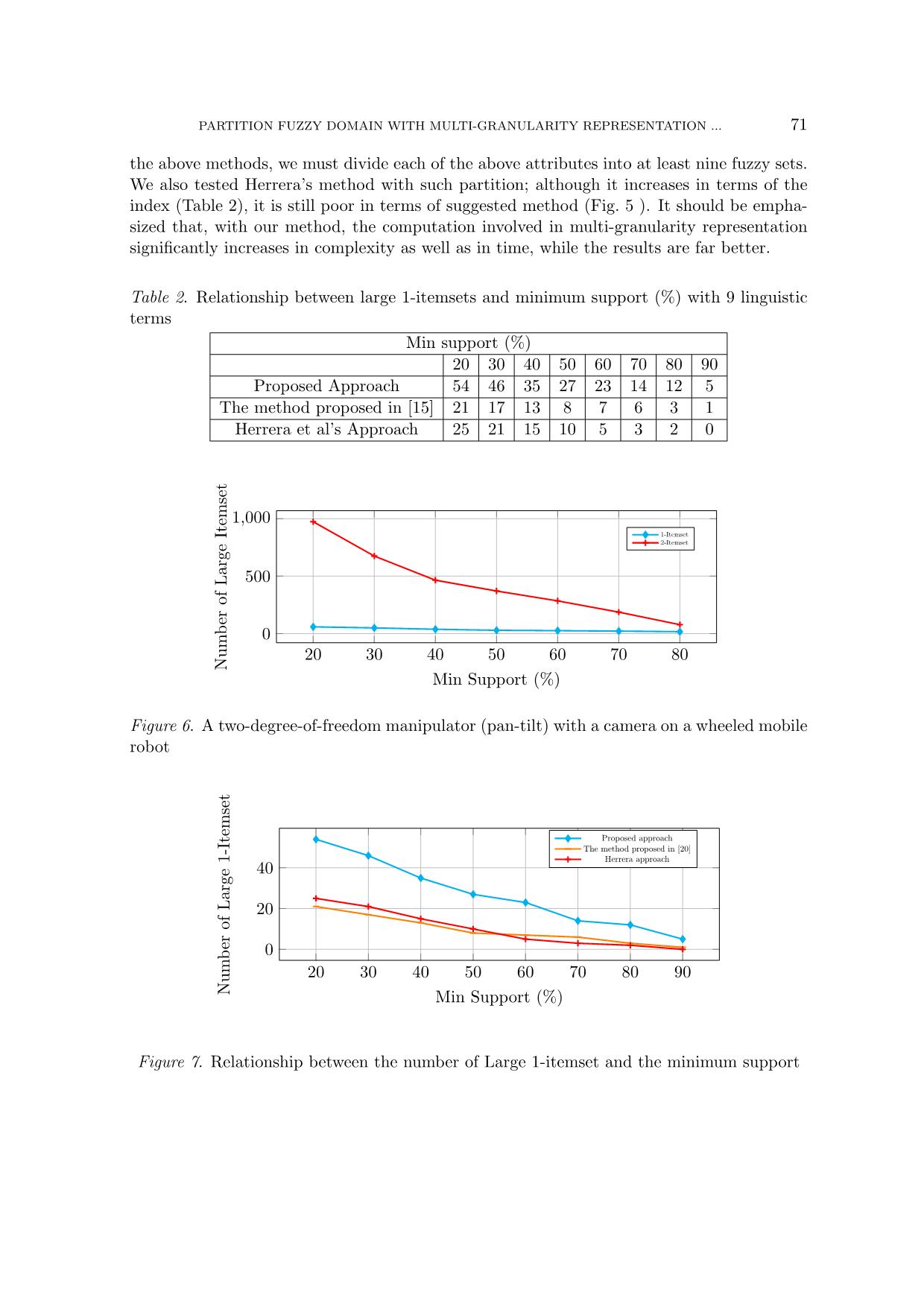
The results compared with other methods are listed in the below Table 2: Herrera’s met-
hod proposed in [1], the method of using HA and sign-granularity was proposed in [20]. Here,
(listing properties that use comparative form: overlay, overlap as the table of the previous
paper), and methods for comparison are performed through single-particle representation.
As given in the introduction, there hasn’t been results regarding the fuzzy association rule
mining using multinomial manifests due to the complexity of the experiment. (The latest
article [18] only mentions an experiment that uses the multi-granularity representation of
regression problems). It can be seen that multi-granularity representation will bring better
results. In addition, as discussed above, in terms of semantics, using multi-granularity re-
presentation will give us rules with different linguistic labels, for example (e.g., 2 fuzzy rules
whose linguistic elements have the length of 1, 2). In order to have similar rules, based on
PARTITION FUZZY DOMAIN WITH MULTI-GRANULARITY REPRESENTATION ... 71
the above methods, we must divide each of the above attributes into at least nine fuzzy sets.
We also tested Herrera’s method with such partition; although it increases in terms of the
index (Table 2), it is still poor in terms of suggested method (Fig. 5 ). It should be empha-
sized that, with our method, the computation involved in multi-granularity representation
significantly increases in complexity as well as in time, while the results are far better.
Table 2. Relationship between large 1-itemsets and minimum support (%) with 9 linguistic
terms
Min support (%)
20 30 40 50 60 70 80 90
Proposed Approach 54 46 35 27 23 14 12 5
The method proposed in [15] 21 17 13 8 7 6 3 1
Herrera et al’s Approach 25 21 15 10 5 3 2 0
20 30 40 50 60 70 80
0
500
1,000
Min Support (%)
N
u
m
b
er
o
f
L
a
rg
e
It
em
se
t
1-Itemset
2-Itemset
Figure 6. A two-degree-of-freedom manipulator (pan-tilt) with a camera on a wheeled mobile
robot
20 30 40 50 60 70 80 90
0
20
40
Min Support (%)N
u
m
b
er
o
f
L
a
rg
e
1
-I
te
m
se
t
Proposed approach
The method proposed in [20]
Herrera approach
Figure 7. Relationship between the number of Large 1-itemset and the minimum support
72 TRAN THAI SON, NGUYEN TUAN ANH
1
1
2-Level
02 V C−LC− LC+ V C+ 12
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
1
1-Level
01 C− C+ 11
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
1
0-Level
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
00 W 10
1
1
0-Level
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
00 W 10
1
1
1-Level
01 C− C+ 11
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
1
2-Level
02V C− LC− LC+ V C+ 12
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
1
2-Level
02V C− LC− LC+ V C+ 12
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
1
1-Level
01 C− C+ 11
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
1
0-Level
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
00 W 10
1
1
0-Level
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
00 W 10
1
1
1-Level
01 C− C+ 11
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
1
2-Level
02 V C− LC− LC+ V C+ 12
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
1
2-Level
02V C− LC− LC+ V C+ 12
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
1
1-Level
01 C− C+ 11
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
1
0-Level
00 W 10
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
1
0-Level
00 W 10
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
1
1-Level
01 C− C+ 11
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
1
2-Level
02 V C− LC− LC+ V C+ 12
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
PARTITION FUZZY DOMAIN WITH MULTI-GRANULARITY REPRESENTATION ... 73
1
1
2-Level
02V C− LC− LC+ V C+12
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
1
1-Level
01C− C+ 11
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
1
0-Level
00 W 10
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
1
0-Level
00 W 10
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
1
1-Level
01C− C+ 11
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
1
2-Level
02V C− LC− LC+ V C+12
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
1
2-Level
02 V C−LC− LC+ V C+ 12
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
1
1-Level
01 C− C+ 11
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
1
0-Level
00 W 10
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
1
0-Level
00 W 10
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
1
1-Level
01 C− C+ 11
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1
1
2-Level
02V C− LC− LC+ V C+ 12
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
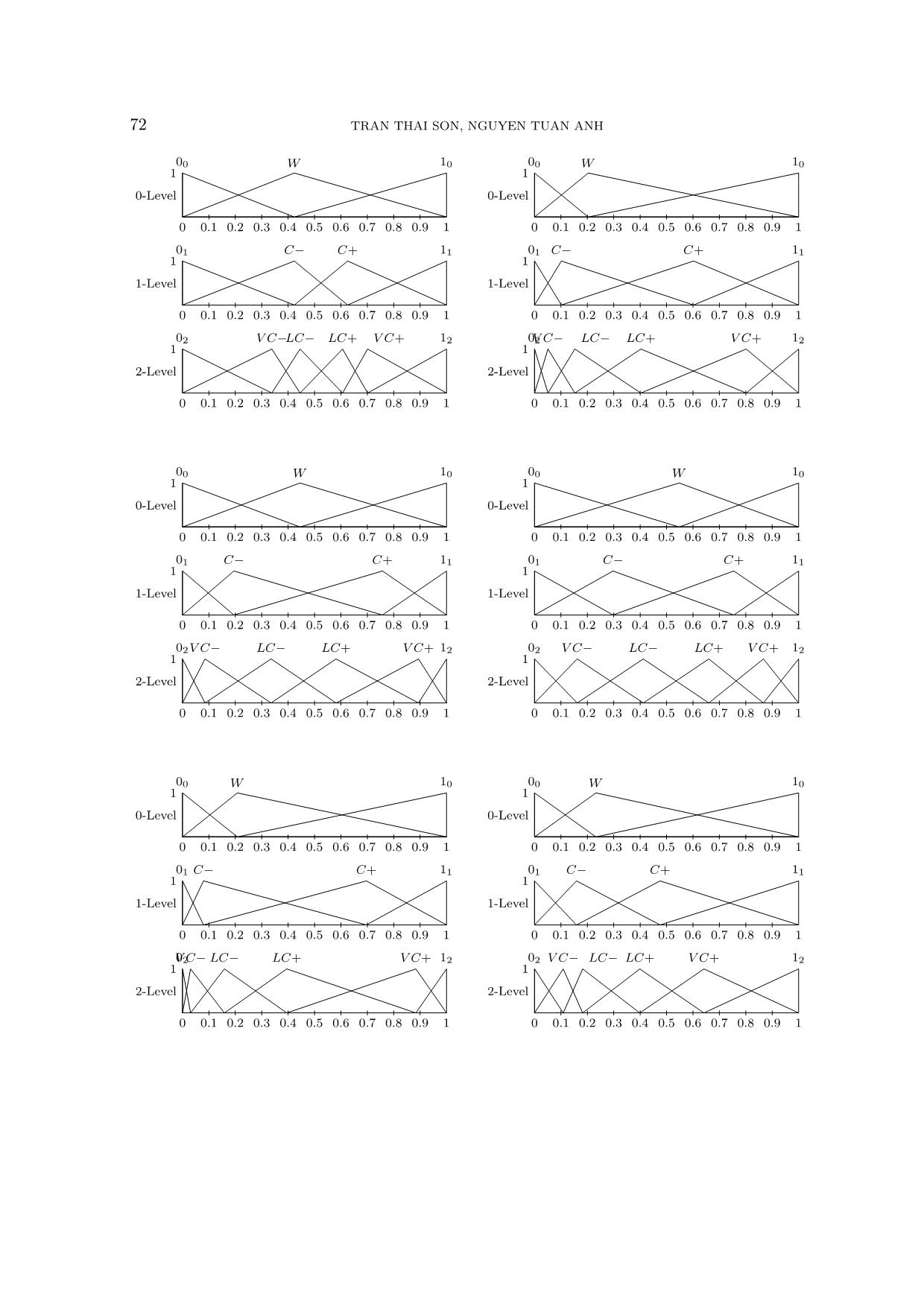
Figure 8. MFs obtained after using GA for optimization
6. CONCLUSIONS
The paper presents the method of mining the association rule according to the hedge
algebra’s approach based on dividing the fuzzy domain of the attribute values according
to the multi-granularity representation. Experimental results based on the database of the
US Census in 1995 showed us the advantage of this method. Firstly, it provides a fairly
simple but effective way of constructing fuzzy sets and dividing value domain of attributes.
Moreover, these fuzzy sets not only ensure the criteria for the fuzzy division system but
also provide a good response in terms of semantics to the explored rules. It means that
the mining rules include both highly generalized and detailed rules, depending on the data
representation layer in the multi-granularity structure we construct based on hedge algebra.
ACKNOWLEDGMENT
This research is funded by Vietnam National Foundation for Science and Technology
Development (NAFOSTED) under Grant No. 102.01-2017.06
74 TRAN THAI SON, NGUYEN TUAN ANH
REFERENCES
[1] J. Alcala´-Fdez, R. Alcala´, M. J. Gacto, and F. Herrera, “Learning the membership function
contexts for mining fuzzy association rules by using genetic algorithms,” Fuzzy Sets and Systems,
vol. 160, no. 7, pp. 905–921, 2009.
[2] J. Alcala-Fdez, R. Alcala, and F. Herrera, “A fuzzy association rule-based classification model
for high-dimensional problems with genetic rule selection and lateral tuning,” IEEE Transactions
on Fuzzy Systems, vol. 19, no. 5, pp. 857–872, 2011.
[3] M. Antonelli, P. Ducange, B. Lazzerini, and F. Marcelloni, “Learning concurrently data and rule
bases of mamdani fuzzy rule-based systems by exploiting a novel interpretability index,” Soft
Computing, vol. 15, no. 10, pp. 1981–1998, 2011.
[4] ——, “Multi-objective evolutionary design of granular rule-based classifiers,” Granular Compu-
ting, vol. 1, no. 1, pp. 37–58, 2016.
[5] G. Castellano, A. M. Fanelli, and C. Mencar, “Fuzzy information granulation with multiple levels
of granularity,” in Granular Computing and Intelligent Systems. Springer, 2011, pp. 185–202.
[6] C.-H. Chen, T. Hong, V. S. Tseng, L.-C. Chen et al., “Multi-objective genetic-fuzzy data mining,”
International Journal of Innovative Computing, 2012.
[7] N. C. Ho, T. T. Son, N. D. Khang, and L. X. Viet, “Fuzziness measure, quantified sematic
mapping and interpolative method of approximate reasoning in medical expert systems.” Journal
of Computer Science and Cybernetics, vol. 18, no. 3, pp. 237–252, 2002.
[8] N. C. Ho and N. Van Long, “Fuzziness measure on complete hedge algebras and quantifying
semantics of terms in linear hedge algebras,” Fuzzy sets and Systems, vol. 158, no. 4, pp. 452–
471, 2007.
[9] T.-P. Hong, C.-H. Chen, Y.-C. Lee, and Y.-L. Wu, “Genetic-fuzzy data mining with divide-and-
conquer strategy,” IEEE Transactions on Evolutionary Computation, vol. 12, no. 2, pp. 252–265,
2008.
[10] C. Mencar, M. Lucarelli, C. Castiello, and A. M. Fanelli, “Design of strong fuzzy partitions from
cuts.” in EUSFLAT Conf., 2013.
[11] C. H. Nguyen, W. Pedrycz, T. L. Duong, and T. S. Tran, “A genetic design of linguistic terms
for fuzzy rule based classifiers,” International Journal of Approximate Reasoning, vol. 54, no. 1,
pp. 1–21, 2013.
[12] C. H. Nguyen, T. S. Tran, and P. D. Phong, “Modeling of a semantics core of linguistic terms
based on an extension of hedge algebra semantics and its application,” Knowledge-Based Systems,
vol. 67, pp. 244–262, 2014.
[13] D. L. Olson and D. Delen, Advanced data mining techniques. Springer Science & Business
Media, 2008.
[14] P. Pulkkinen and H. Koivisto, “A dynamically constrained multiobjective genetic fuzzy system
for regression problems,” IEEE Transactions on Fuzzy Systems, vol. 18, no. 1, pp. 161–177, 2010.
[15] N. T. A. Tran Thai Son, “Hedges algebras and fuzzy partition problem for qualitative attributes,”
ournal of Computer Science and Cybernetics, vol. 32, no. 4, 2016.
PARTITION FUZZY DOMAIN WITH MULTI-GRANULARITY REPRESENTATION ... 75
[16] D. Wijayasekara and M. Manic, “Data driven fuzzy membership function generation for increased
understandability,” in Fuzzy Systems (FUZZ-IEEE), 2014 IEEE International Conference on.
IEEE, 2014, pp. 133–140.
[17] Y. Yao, “A triarchic theory of granular computing,” Granular Computing, vol. 1, no. 2, pp.
145–157, 2016.
[18] L. A. Zadeh, “The concept of a linguistic variable and its application to approximate reasoningi,”
Information sciences, vol. 8, no. 3, pp. 199–249, 1975.
Received on October 10, 2017
Revised on April 20, 2018