Multiple plane fitting algorithm to evaluate the accuracy of 3D point cloud using structured light measurement

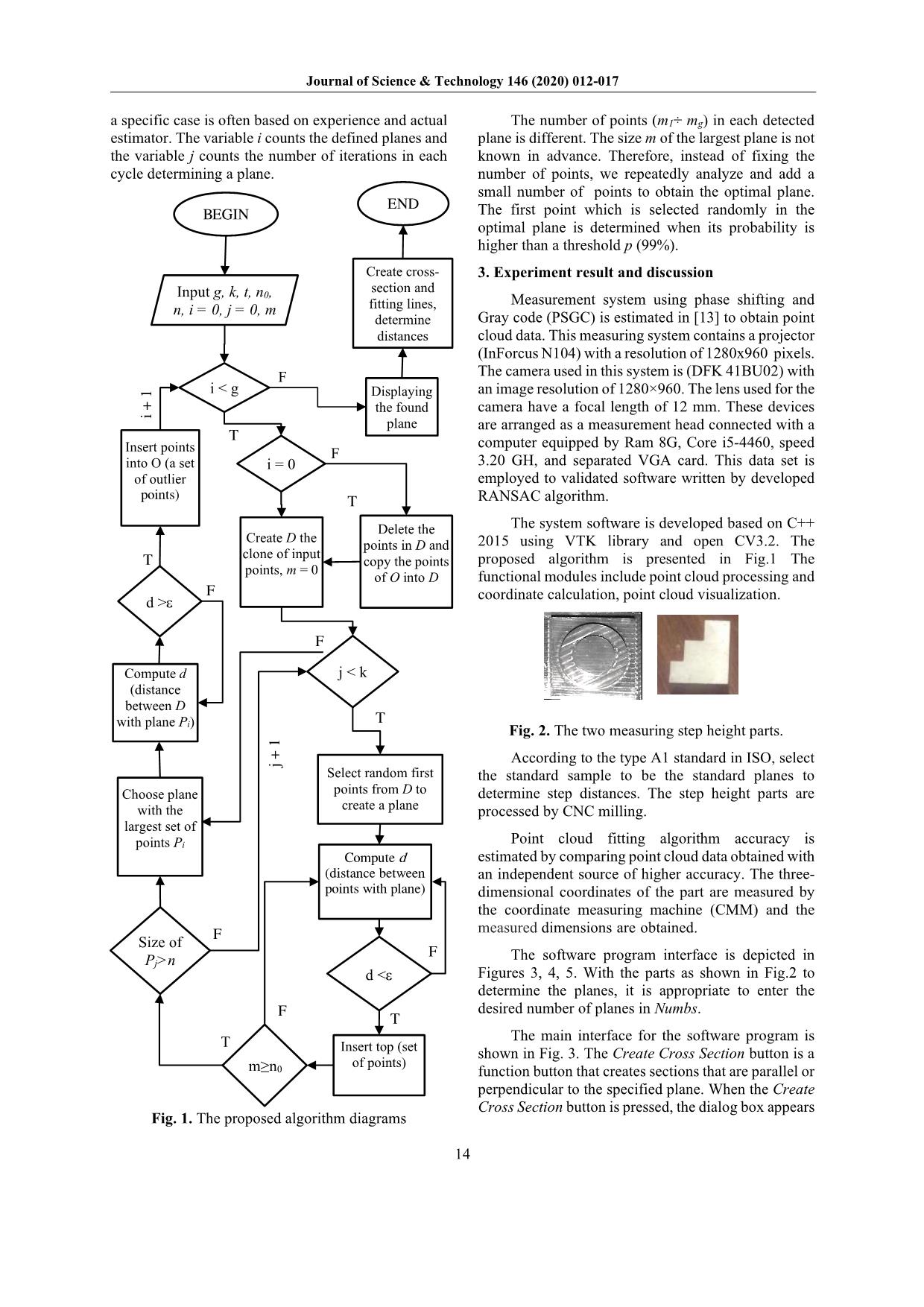
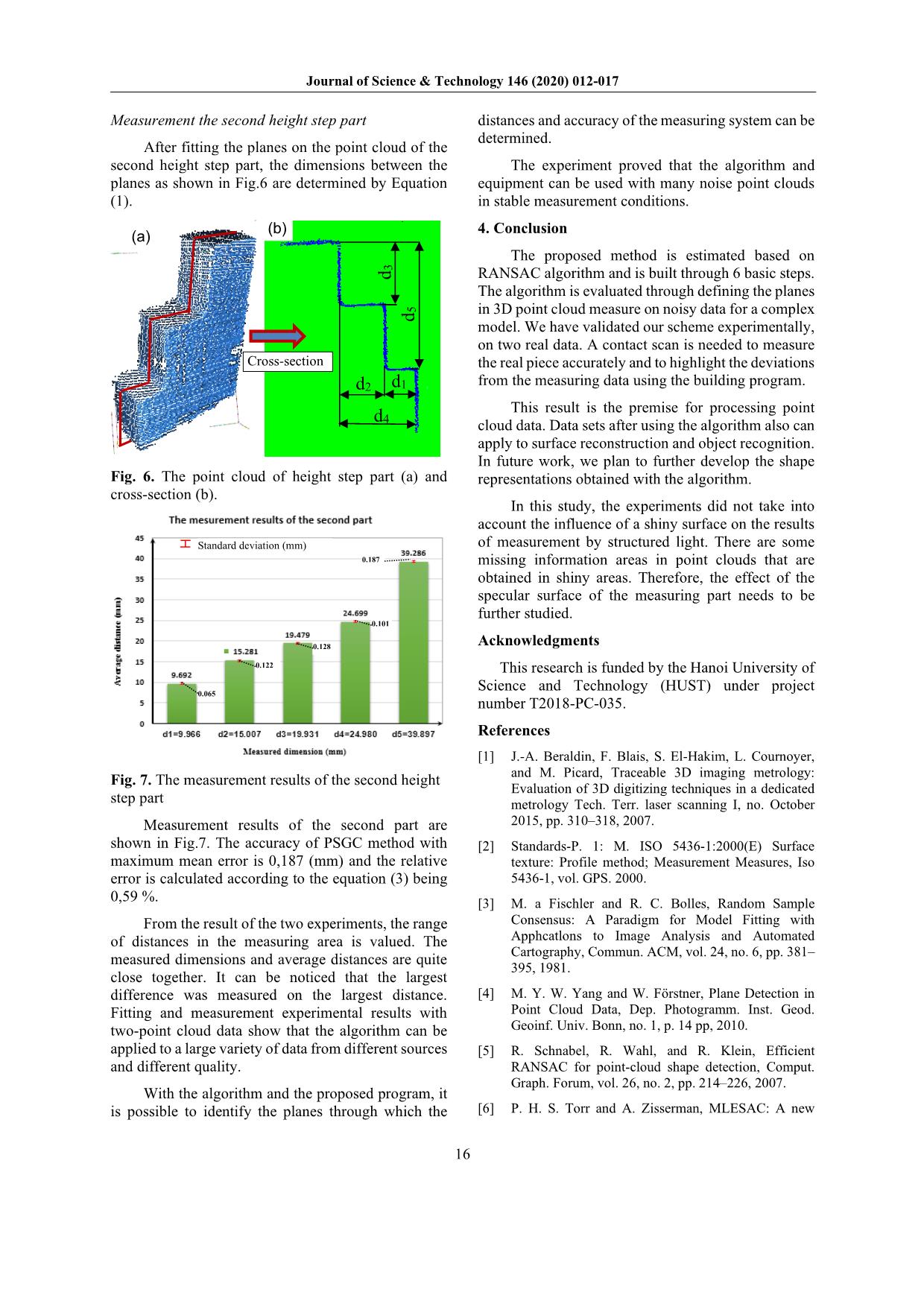
hich distances between planes are 
calculated [12]. The precise processing of point clouds 
with the detection of planes is essential to measure the 
size and relative positions of the surfaces properly. In 
this paper, the system’s accuracy is evaluated by the 
step standard. The measurement plane is determined 
through the distances of planes. 
The experiments have been carried out to value 
the measurement system accuracy. The plane fitting 
algorithm in the input data is developed by employing 
RANSAC algorithm. The proposed algorithm can 
detect multiple planes on the noisy complex data. 
2. Measurement dimensions in the 3D point cloud 
2.1 Multiple planes fitting algorithm 
In our case, the planes are fitted the model to 
measure some dimensions in 3D point cloud. The 
multiple planes are fitted as clusters which group the 
points supporting the same plane by employing the 
proposed algorithm. 
The fitting strategy for multiple planes g in data 
point cloud N of size n is designed. The processing can 
be further decomposed into six steps as the following: 
1: Create the clone D of input point cloud N. 3 points 
A, B, C in data set D are randomly selected to compute 
the parameters. The general model of 3D plane (P) can 
be passed through any 3 selected points. The plane (P) 
is defined with vector pairs AB
 
; AC
 
 and the normal 
vector of the plane is ;n AB AC =  
  
2: The number of inliers m1 is determined by 
comparing the distance d from each point in the D to 
the calculated plane less than a threshold ε (di<ε). This 
process is repeated until the number of inliers m1 is big 
enough or the number of iterations has been reached to 
k with the probability of p being 95%. The plane P1 is 
defined with m1 points. Then the inliers n1 are 
extracted from the clone D. A set of outlier points O 
with size (n0-n1) are finding in condition di >ε. 
3: Remove the points in D and copy the O into D. 
4: Repeat step 2 to 3 until all planes P2 ÷ Pg are 
detected. 
5: Show the input point cloud P0 and the number fitting 
planes Pg. 
6: The fitting planes are cut in a perpendicular or 
parallel direction to determine distances. On the 
cutting plane, it is necessary to identify the 
characteristic straight lines. On the cross-section, the 
fittest lines are detected and distances between them 
are measured. The detected planes are reached and 
display. 
2.2 Dimension calculation 
The cross-sections are cut perpendicular or 
parallel to the detected planes to determine the 
dimensions. Fitting multiple lines in each cross-section 
is applied. 
The distance between featured lines hi is defined. 
Then the distances are compared with measured 
distance ht 
The mean distance µ between any two planes and 
the standard deviation σ can be calculated as follows: 
1
1 gn
i
ig
h
n
µ
=
= ∑ (1) 
( )2
1
1
1
n
i
i
h
n
σ µ
=
= −
− ∑ (2) 
The relative error (RE) can be presented as: 
.100% .100%t i
t t
h h hRE
h h
− ∆
= = (3) 
where: h∆ is the average deviation of the 
measurement dimensions. The algorithm is started 
with entering parameters including 3D point cloud 
data, the number of detected plane g, the number of 
iterations k, the threshold ε.. The determination of ε on 
Journal of Science & Technology 146 (2020) 012-017 
14 
a specific case is often based on experience and actual 
estimator. The variable i counts the defined planes and 
the variable j counts the number of iterations in each 
cycle determining a plane. 
Fig. 1. The proposed algorithm diagrams 
The number of points (m1÷ mg) in each detected 
plane is different. The size m of the largest plane is not 
known in advance. Therefore, instead of fixing the 
number of points, we repeatedly analyze and add a 
small number of points to obtain the optimal plane. 
The first point which is selected randomly in the 
optimal plane is determined when its probability is 
higher than a threshold p (99%). 
3. Experiment result and discussion 
Measurement system using phase shifting and 
Gray code (PSGC) is estimated in [13] to obtain point 
cloud data. This measuring system contains a projector 
(InForcus N104) with a resolution of 1280x960 pixels. 
The camera used in this system is (DFK 41BU02) with 
an image resolution of 1280×960. The lens used for the 
camera have a focal length of 12 mm. These devices 
are arranged as a measurement head connected with a 
computer equipped by Ram 8G, Core i5-4460, speed 
3.20 GH, and separated VGA card. This data set is 
employed to validated software written by developed 
RANSAC algorithm. 
The system software is developed based on C++ 
2015 using VTK library and open CV3.2. The 
proposed algorithm is presented in Fig.1 The 
functional modules include point cloud processing and 
coordinate calculation, point cloud visualization. 
Fig. 2. The two measuring step height parts. 
According to the type A1 standard in ISO, select 
the standard sample to be the standard planes to 
determine step distances. The step height parts are 
processed by CNC milling. 
Point cloud fitting algorithm accuracy is 
estimated by comparing point cloud data obtained with 
an independent source of higher accuracy. The three-
dimensional coordinates of the part are measured by 
the coordinate measuring machine (CMM) and the 
measured dimensions are obtained. 
The software program interface is depicted in 
Figures 3, 4, 5. With the parts as shown in Fig.2 to 
determine the planes, it is appropriate to enter the 
desired number of planes in Numbs. 
The main interface for the software program is 
shown in Fig. 3. The Create Cross Section button is a 
function button that creates sections that are parallel or 
perpendicular to the specified plane. When the Create 
Cross Section button is pressed, the dialog box appears 
Create cross-
section and 
fitting lines, 
determine 
distances 
F 
T 
j +
 1
T 
T 
T F 
T 
F 
T 
T 
Select random first 
points from D to 
create a plane 
Compute d 
(distance between 
points with plane) 
d <ε 
Insert top (set 
of points) 
Choose plane 
with the 
largest set of 
points Pi 
Size of 
Pj>n 
i +
 1
j < k 
Create D the 
clone of input 
points, m = 0 
i = 0 
d >ε 
Compute d 
(distance 
between D 
with plane Pi) 
Insert points 
into O (a set 
of outlier 
points) 
Delete the 
points in D and 
copy the points 
of O into D 
 m≥n0 
BEGIN 
Input g, k, t, n0, 
n, i = 0, j = 0, m 
i < g Displaying 
the found 
plane 
END 
F 
F 
F 
F 
Journal of Science & Technology 146 (2020) 012-017 
15 
as shown in Fig.4. The distance in the y-direction of 
the part is determined and shown on the first line of 
Dental 0 to 51. 73. Thus, the distance of the cutting 
plane relative to the root of the y axis should be entered 
in the function block, as shown in Fig. 4 is 29. 
After the cross-section is obtained at the cutting 
position as shown in Fig.5, enter the number of lines 
to fit in the Number line to fit box, as shown in Fig.5. 
The distance between the lines will be determined by 
entering the name of the line in cells 1 and line 2, 
where line1 is the number line 2 and line 2 is the 
number line 3. The result of determining the range of 
lines in the different sections is shown in the 
measurement data box. It will then be saved to an excel 
file when the export data button is clicked. 
 Cross-sections are created to measure 
dimensions. The cross-section of the step height was 
sampled 30 times on the length or width of the detected 
plane. 
In this section, we illustrate the features of our 
algorithm on two examples. Two parts were employed 
for evaluating the precision of the algorithm. The 
number of measurements is implemented in the same 
temperature condition of 25oC, environment light is 
kept steadily from 100 to 200 (lux). 
Measurement of the first height step part 
In this experiment, the height step part with small 
nominal dimensions Z21= 3 mm and Z23 = 5 mm were 
measured. 
This is height measurement results of stepped 
part with 30 cross-sections of 0.5 mm spacing. On the 
cross-section, the fittest lines are detected and 
distances between them are measured. The measured 
dimensions of the height step part are measured by the 
coordinate measuring machine (CMM). The CMM 
instrument chosen was the Microstar 220-162 DCC 
coordinate measuring device of Helmel Engineering 
Products, Inc at the Measurement Center - Vietnam 
Technology Institute The CMM has specifications: 
resolution, 0.5 µm; repeatability, 2.8 µm; and 
volumetric accuracy, 11.2 µm. The results of contact 
scanning and CMM measurements presented in this 
work are taken as reference geometry. 
The first part measurement results obtained with 
the proposed algorithm are shown in Table 1. 
Measurement results of the first part show the 
accuracy of PSGC method with maximum mean error 
is 0.078 (mm) and the relative error is calculated 
according to the equation (3) being 1,46% 
The second part measurement results with 30 
cross-sections have a distance between each section is 
0.4 mm. On the cross-section, the fittest lines are 
detected and distances between them are measured 
Table 1. The measurement results of the first part. 
Measured 
dimension 
(mm) 
Average 
distance 
(mm) 
Mean 
error 
(mm) 
Standard 
deviation 
(mm) 
Z21=2.936 2.865 0.071 0.068 
Z23=4.991 4.913 0.078 0.049 
 Fig. 3. Display of fitting software 
 Fig. 4. Display of create cross-section function 
 Fig. 5. Display of fitting line function 
 Part 
line 3 
line 2
 line 1 
Cross -section 
Data 
measurement 
Z21 
Z23
Journal of Science & Technology 146 (2020) 012-017 
16 
Measurement the second height step part 
After fitting the planes on the point cloud of the 
second height step part, the dimensions between the 
planes as shown in Fig.6 are determined by Equation 
(1). 
Fig. 6. The point cloud of height step part (a) and 
cross-section (b). 
Fig. 7. The measurement results of the second height 
step part 
Measurement results of the second part are 
shown in Fig.7. The accuracy of PSGC method with 
maximum mean error is 0,187 (mm) and the relative 
error is calculated according to the equation (3) being 
0,59 %. 
From the result of the two experiments, the range 
of distances in the measuring area is valued. The 
measured dimensions and average distances are quite 
close together. It can be noticed that the largest 
difference was measured on the largest distance. 
Fitting and measurement experimental results with 
two-point cloud data show that the algorithm can be 
applied to a large variety of data from different sources 
and different quality. 
With the algorithm and the proposed program, it 
is possible to identify the planes through which the 
distances and accuracy of the measuring system can be 
determined. 
The experiment proved that the algorithm and 
equipment can be used with many noise point clouds 
in stable measurement conditions. 
4. Conclusion 
The proposed method is estimated based on 
RANSAC algorithm and is built through 6 basic steps. 
The algorithm is evaluated through defining the planes 
in 3D point cloud measure on noisy data for a complex 
model. We have validated our scheme experimentally, 
on two real data. A contact scan is needed to measure 
the real piece accurately and to highlight the deviations 
from the measuring data using the building program. 
This result is the premise for processing point 
cloud data. Data sets after using the algorithm also can 
apply to surface reconstruction and object recognition. 
In future work, we plan to further develop the shape 
representations obtained with the algorithm. 
In this study, the experiments did not take into 
account the influence of a shiny surface on the results 
of measurement by structured light. There are some 
missing information areas in point clouds that are 
obtained in shiny areas. Therefore, the effect of the 
specular surface of the measuring part needs to be 
further studied. 
Acknowledgments 
This research is funded by the Hanoi University of 
Science and Technology (HUST) under project 
number T2018-PC-035. 
References 
[1] J.-A. Beraldin, F. Blais, S. El-Hakim, L. Cournoyer, 
and M. Picard, Traceable 3D imaging metrology: 
Evaluation of 3D digitizing techniques in a dedicated 
metrology Tech. Terr. laser scanning I, no. October 
2015, pp. 310–318, 2007. 
[2] Standards-P. 1: M. ISO 5436-1:2000(E) Surface 
texture: Profile method; Measurement Measures, Iso 
5436-1, vol. GPS. 2000. 
[3] M. a Fischler and R. C. Bolles, Random Sample 
Consensus: A Paradigm for Model Fitting with 
Apphcatlons to Image Analysis and Automated 
Cartography, Commun. ACM, vol. 24, no. 6, pp. 381–
395, 1981. 
[4] M. Y. W. Yang and W. Förstner, Plane Detection in 
Point Cloud Data, Dep. Photogramm. Inst. Geod. 
Geoinf. Univ. Bonn, no. 1, p. 14 pp, 2010. 
[5] R. Schnabel, R. Wahl, and R. Klein, Efficient 
RANSAC for point-cloud shape detection, Comput. 
Graph. Forum, vol. 26, no. 2, pp. 214–226, 2007. 
[6] P. H. S. Torr and A. Zisserman, MLESAC: A new 
d1 
d 3
d2 
d4 
d 5
 Cross-section 
 (a) (b) 
Standard deviation (mm) 
0.065 
0.122 
0.128 
0.101 
0.187 
Journal of Science & Technology 146 (2020) 012-017 
17 
robust estimator with application to estimating image 
geometry, Comput. Vis. Image Underst., vol. 78, no. 1, 
pp. 138–156, 2000. 
[7] S. Huang, Y. Liu, N. Gao, and Z. Zhang, Distance 
Calibration between Reference Plane and Screen in 
Direct Phase Measuring Deflectometry, 2018. 
[8] B. J. Tordoff and D. W. Murray, Guided-MLESAC: 
Faster image transform estimation by using matching 
priors, IEEE Trans. Pattern Anal. Mach. Intell., vol. 27, 
no. 10, pp. 1523–1535, 2005. 
[9] O. Galo, R. Manduchi, and A. Rafii, CC-RANSAC: 
Fitting planes in the presence of multiple surfaces in 
range data, Pattern Recognit. Lett., vol. 32, no. 3, pp. 
403–410, 2011. 
[10] A. Vedaldi, H. Tin, P. Favaro, and S. Soatto, 
KALMANSAC: Robust filtering by consensus, Proc. 
IEEE Int. Conf. Comput. Vis., vol. I, pp. 633–640, 
2005. 
[11] H. Wang and D. Suter, Robust adaptive-scale 
parametric model estimation for computer vision, 
IEEE Trans. Pattern Anal. Mach. Intell., vol. 26, no. 
11, pp. 1459–1474, 2004. 
[12] L. Li, F. Yang, H. Zhu, D. Li, Y. Li, and L. Tang, An 
improved RANSAC for 3D point cloud plane 
segmentation based on normal distribution 
transormation cells, Remote Sens., vol. 9, no. 5, 2017. 
[13] Nguyen Thi Kim Cuc, Nguyen Van Vinh, Nguyen 
Thanh Hung, Nguyen Viet Kien, Improving the 
Accuracy of the Calibration Method for Structured 
Light System, Journal of Science & Technology 127 
(2018) 016-021.