Một thuật toán hiệu quả để trích xuất tập Skyline

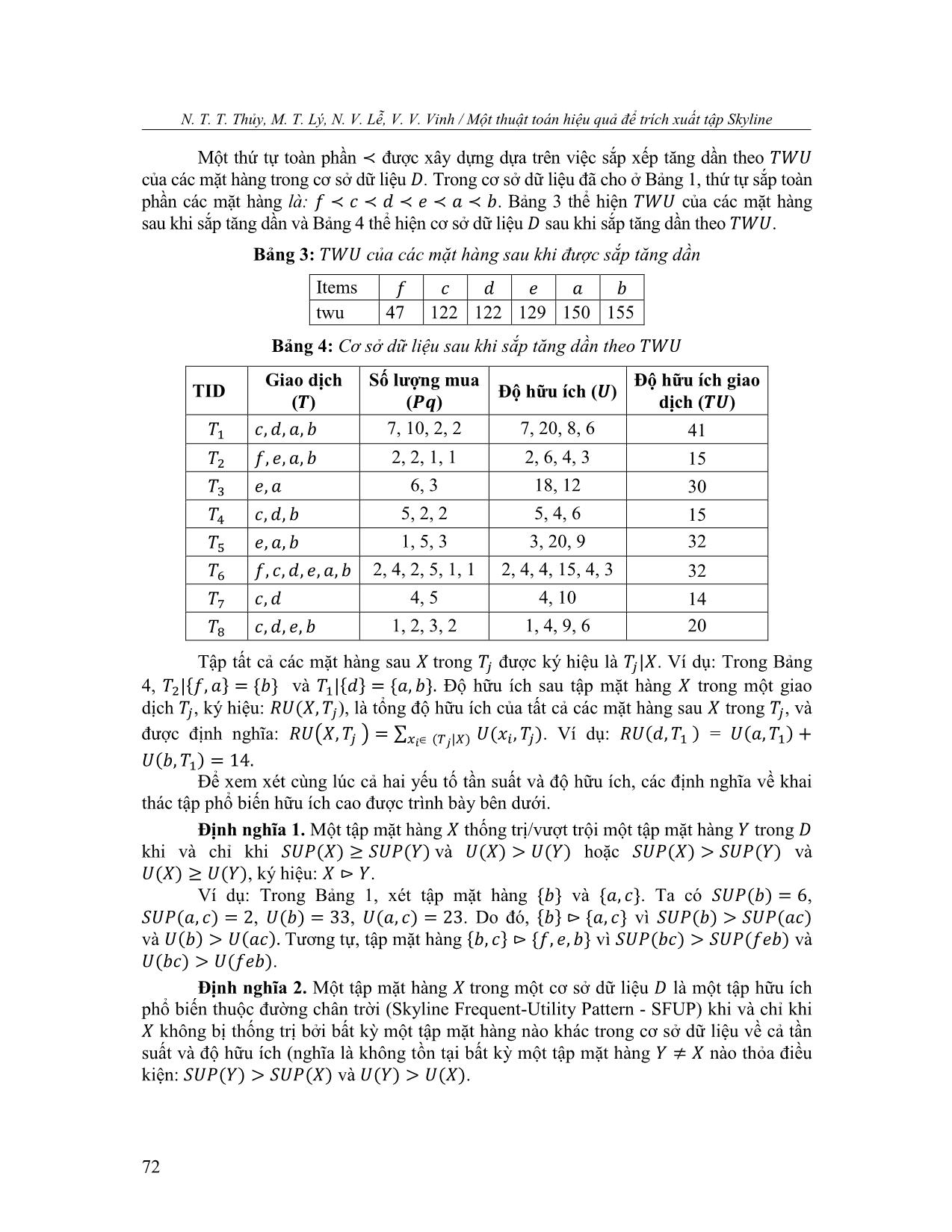
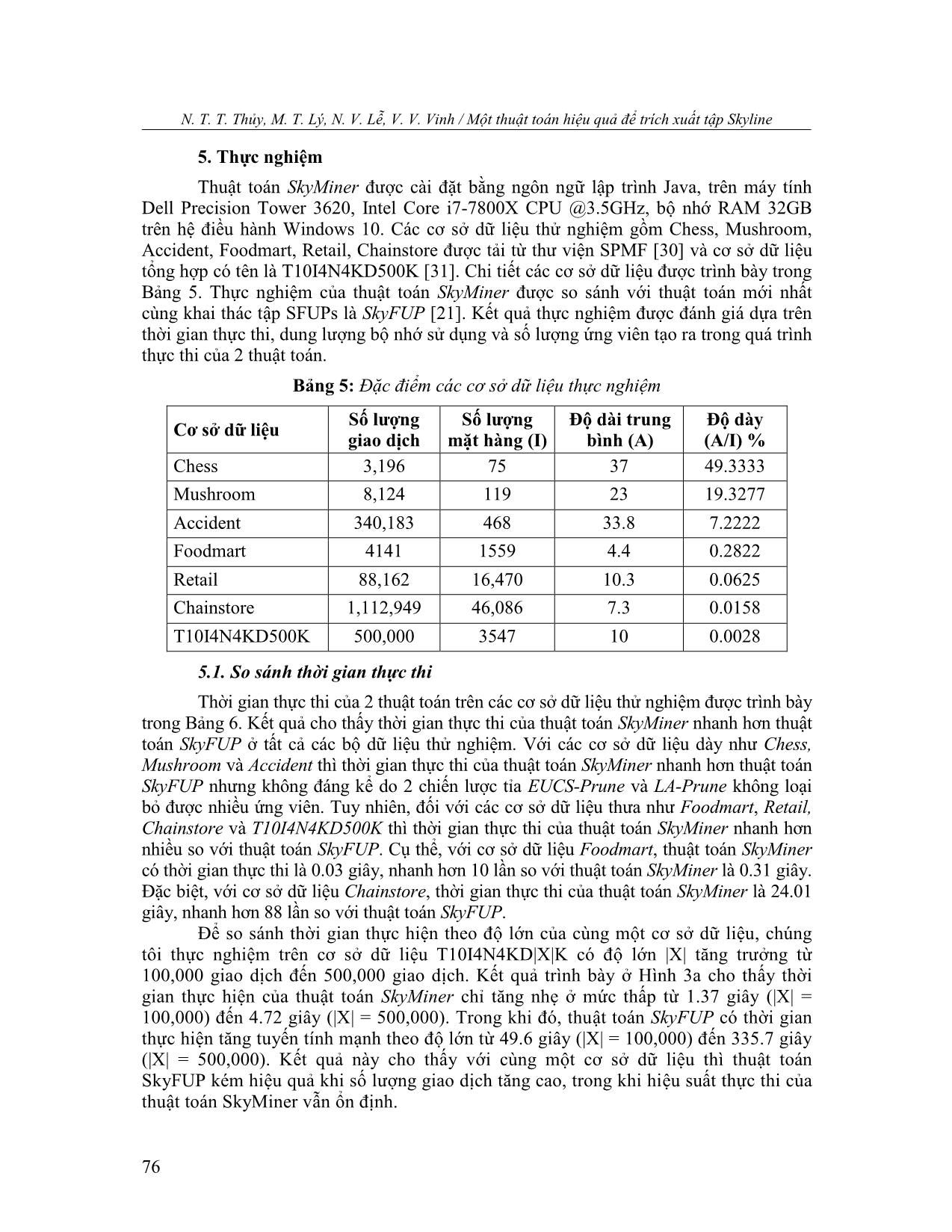
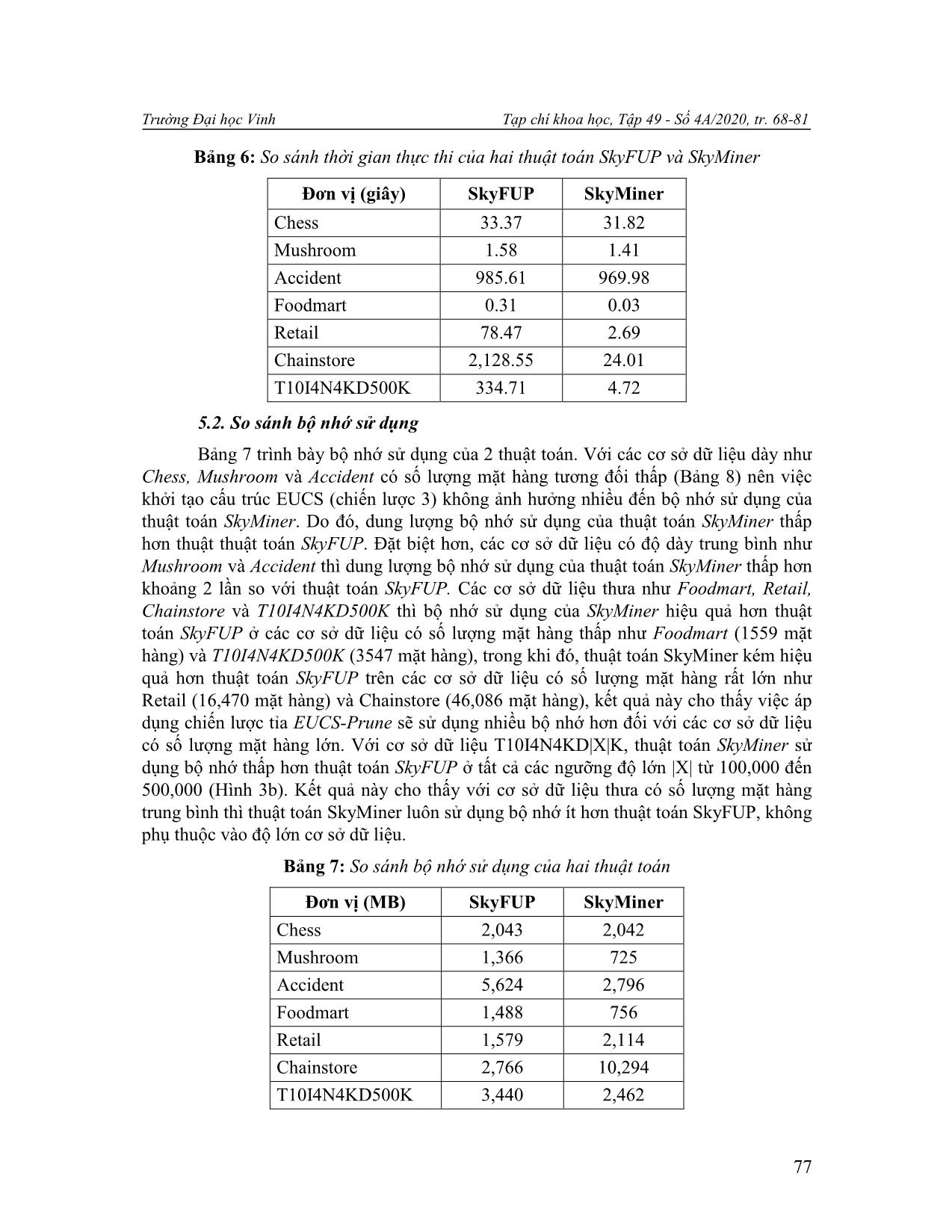
 áp dụng chiến lược tỉa LA-Prune 
15. return null; 
16. end if 
17. Continue; 
18. end if 
19. end for 
20. return ; 
 75 
 N. T. T. Thủy, M. T. Lý, N. V. Lễ, V. V. Vinh / Một thuật toán hiệu quả để trích xuất tập Skyline 
 5. Thực nghiệm 
 Thuật toán SkyMiner được cài đặt bằng ngôn ngữ lập trình Java, trên máy tính 
Dell Precision Tower 3620, Intel Core i7-7800X CPU @3.5GHz, bộ nhớ RAM 32GB 
trên hệ điều hành Windows 10. Các cơ sở dữ liệu thử nghiệm gồm Chess, Mushroom, 
Accident, Foodmart, Retail, Chainstore được tải từ thư viện SPMF [30] và cơ sở dữ liệu 
tổng hợp có tên là T10I4N4KD500K [31]. Chi tiết các cơ sở dữ liệu được trình bày trong 
Bảng 5. Thực nghiệm của thuật toán SkyMiner được so sánh với thuật toán mới nhất 
cùng khai thác tập SFUPs là SkyFUP [21]. Kết quả thực nghiệm được đánh giá dựa trên 
thời gian thực thi, dung lượng bộ nhớ sử dụng và số lượng ứng viên tạo ra trong quá trình 
thực thi của 2 thuật toán. 
 Bảng 5: Đặc điểm các cơ sở dữ liệu thực nghiệm 
 Số lượng Số lượng Độ dài trung Độ dày 
 Cơ sở dữ liệu 
 giao dịch mặt hàng (I) bình (A) (A/I) % 
 Chess 3,196 75 37 49.3333 
 Mushroom 8,124 119 23 19.3277 
 Accident 340,183 468 33.8 7.2222 
 Foodmart 4141 1559 4.4 0.2822 
 Retail 88,162 16,470 10.3 0.0625 
 Chainstore 1,112,949 46,086 7.3 0.0158 
 T10I4N4KD500K 500,000 3547 10 0.0028 
 5.1. So sánh thời gian thực thi 
 Thời gian thực thi của 2 thuật toán trên các cơ sở dữ liệu thử nghiệm được trình bày 
trong Bảng 6. Kết quả cho thấy thời gian thực thi của thuật toán SkyMiner nhanh hơn thuật 
toán SkyFUP ở tất cả các bộ dữ liệu thử nghiệm. Với các cơ sở dữ liệu dày như Chess, 
Mushroom và Accident thì thời gian thực thi của thuật toán SkyMiner nhanh hơn thuật toán 
SkyFUP nhưng không đáng kể do 2 chiến lược tỉa EUCS-Prune và LA-Prune không loại 
bỏ được nhiều ứng viên. Tuy nhiên, đối với các cơ sở dữ liệu thưa như Foodmart, Retail, 
Chainstore và T10I4N4KD500K thì thời gian thực thi của thuật toán SkyMiner nhanh hơn 
nhiều so với thuật toán SkyFUP. Cụ thể, với cơ sở dữ liệu Foodmart, thuật toán SkyMiner 
có thời gian thực thi là 0.03 giây, nhanh hơn 10 lần so với thuật toán SkyMiner là 0.31 giây. 
Đặc biệt, với cơ sở dữ liệu Chainstore, thời gian thực thi của thuật toán SkyMiner là 24.01 
giây, nhanh hơn 88 lần so với thuật toán SkyFUP. 
 Để so sánh thời gian thực hiện theo độ lớn của cùng một cơ sở dữ liệu, chúng 
tôi thực nghiệm trên cơ sở dữ liệu T10I4N4KD|X|K có độ lớn |X| tăng trưởng từ 
100,000 giao dịch đến 500,000 giao dịch. Kết quả trình bày ở Hình 3a cho thấy thời 
gian thực hiện của thuật toán SkyMiner chỉ tăng nhẹ ở mức thấp từ 1.37 giây (|X| = 
100,000) đến 4.72 giây (|X| = 500,000). Trong khi đó, thuật toán SkyFUP có thời gian 
thực hiện tăng tuyến tính mạnh theo độ lớn từ 49.6 giây (|X| = 100,000) đến 335.7 giây 
(|X| = 500,000). Kết quả này cho thấy với cùng một cơ sở dữ liệu thì thuật toán 
SkyFUP kém hiệu quả khi số lượng giao dịch tăng cao, trong khi hiệu suất thực thi của 
thuật toán SkyMiner vẫn ổn định. 
 76 
Trường Đại học Vinh Tạp chí khoa học, Tập 49 - Số 4A/2020, tr. 68-81 
 Bảng 6: So sánh thời gian thực thi của hai thuật toán SkyFUP và SkyMiner 
 Đơn vị (giây) SkyFUP SkyMiner 
 Chess 33.37 31.82 
 Mushroom 1.58 1.41 
 Accident 985.61 969.98 
 Foodmart 0.31 0.03 
 Retail 78.47 2.69 
 Chainstore 2,128.55 24.01 
 T10I4N4KD500K 334.71 4.72 
 5.2. So sánh bộ nhớ sử dụng 
 Bảng 7 trình bày bộ nhớ sử dụng của 2 thuật toán. Với các cơ sở dữ liệu dày như 
Chess, Mushroom và Accident có số lượng mặt hàng tương đối thấp (Bảng 8) nên việc 
khởi tạo cấu trúc EUCS (chiến lược 3) không ảnh hưởng nhiều đến bộ nhớ sử dụng của 
thuật toán SkyMiner. Do đó, dung lượng bộ nhớ sử dụng của thuật toán SkyMiner thấp 
hơn thuật thuật toán SkyFUP. Đặt biệt hơn, các cơ sở dữ liệu có độ dày trung bình như 
Mushroom và Accident thì dung lượng bộ nhớ sử dụng của thuật toán SkyMiner thấp hơn 
khoảng 2 lần so với thuật toán SkyFUP. Các cơ sở dữ liệu thưa như Foodmart, Retail, 
Chainstore và T10I4N4KD500K thì bộ nhớ sử dụng của SkyMiner hiệu quả hơn thuật 
toán SkyFUP ở các cơ sở dữ liệu có số lượng mặt hàng thấp như Foodmart (1559 mặt 
hàng) và T10I4N4KD500K (3547 mặt hàng), trong khi đó, thuật toán SkyMiner kém hiệu 
quả hơn thuật toán SkyFUP trên các cơ sở dữ liệu có số lượng mặt hàng rất lớn như 
Retail (16,470 mặt hàng) và Chainstore (46,086 mặt hàng), kết quả này cho thấy việc áp 
dụng chiến lược tỉa EUCS-Prune sẽ sử dụng nhiều bộ nhớ hơn đối với các cơ sở dữ liệu 
có số lượng mặt hàng lớn. Với cơ sở dữ liệu T10I4N4KD|X|K, thuật toán SkyMiner sử 
dụng bộ nhớ thấp hơn thuật toán SkyFUP ở tất cả các ngưỡng độ lớn |X| từ 100,000 đến 
500,000 (Hình 3b). Kết quả này cho thấy với cơ sở dữ liệu thưa có số lượng mặt hàng 
trung bình thì thuật toán SkyMiner luôn sử dụng bộ nhớ ít hơn thuật toán SkyFUP, không 
phụ thuộc vào độ lớn cơ sở dữ liệu. 
 Bảng 7: So sánh bộ nhớ sử dụng của hai thuật toán 
 Đơn vị (MB) SkyFUP SkyMiner 
 Chess 2,043 2,042 
 Mushroom 1,366 725 
 Accident 5,624 2,796 
 Foodmart 1,488 756 
 Retail 1,579 2,114 
 Chainstore 2,766 10,294 
 T10I4N4KD500K 3,440 2,462 
 77 
 N. T. T. Thủy, M. T. Lý, N. V. Lễ, V. V. Vinh / Một thuật toán hiệu quả để trích xuất tập Skyline 
 5.3. So sánh số lượng ứng viên 
 Bảng 8: So sánh số lượng ứng viên phát sinh của hai thuật toán 
 Đơn vị (ứng viên) SkyFUP SkyMiner 
 Chess 3,397,909 2,552,448 
 Mushroom 40,949 32,565 
 Accident 2,555,599 1,889,989 
 Foodmart 39,721 2,190 
 Retail 5,158,951 857,461 
 Chainstore 30,426,801 1,072,259 
 T10I4N4KD500K 6,108,502 50,534 
 Bảng 8 trình bày số lượng ứng viên tạo ra trong quá trình khai thác của hai 
thuật toán trên tập các cơ sở dữ liệu thực nghiệm. Kết quả cho thấy với các cơ sở dữ liệu 
dày như Chess, Mushroom và Accident thì thuật toán SkyMiner tỉa ứng viên tốt hơn thuật 
toán SkyFUP, tuy nhiên, sự chênh lệch là không đáng kể. Với các cơ sở dữ liệu thưa như 
Foodmart, Retail, Chainstore và T10I4N4KD500K, thuật toán SkyMiner cho thấy hiệu 
quả cắt tỉa ứng viên vượt trội so với thuật toán SkyFUP. Số lượng ứng viên do thuật toán 
SkyMiner sinh ra ít hơn từ 6 đến 120 lần so với thuật toán SkyFUP. Với cơ sở dữ liệu 
T10I4N4KD|X|K, kích thước cơ sở dữ liệu tăng từ 100,000 đến 500,000 thì số lượng ứng 
viên sinh ra của thuật toán SkyMiner ít hơn nhiều so với thuật toán SkyFUP (Hình 3c). 
Cụ thể, thuật toán SkyMiner sinh ra từ 45,200 đến 50,534 ứng viên, trong khi số lượng 
ứng viên sinh ra của thuật toán SkyFUP từ 2,497,428 đến 6,108,502. Kết quả này chứng 
tỏ rằng các chiến lược tỉa được áp dụng trong thuật toán SkyMiner đã làm giảm số lượng 
ứng viên một cách đáng kể, từ đó tăng hiệu suất thực thi của thuật toán, đặt biệt với hai 
chiến lược tỉa LA-Prune và EUCS-Prune. 
 Hình 3: So sánh hiệu suất thực thi trên cơ sở dữ liệu T10I4N4KD|X|K 
 6. Kết luận 
 Bài báo này đề xuất thuật toán SkyMiner để khai thác SFUPs trên cơ sở dữ liệu 
giao dịch dựa trên độ hữu ích và tần suất xuất hiện của tập mặt hàng. Cấu trúc utility-list 
 78 
Trường Đại học Vinh Tạp chí khoa học, Tập 49 - Số 4A/2020, tr. 68-81 
được sử dụng để tổ chức, lưu trữ dữ liệu trong quá trình khai thác. Ngoài chiến lược tỉa 
U-Prune đã được áp dụng trong các thuật toán khai thác tập SFUPs trước đây, chúng tôi 
áp dụng thêm hai chiến lược tỉa là LA-Prune và EUCS-Prune để tăng hiệu suất thực thi 
của thuật toán. Kết quả thực nghiệm cho thấy thuật toán SkyMiner cho kết quả tốt hơn 
thuật toán mới nhất là SkyFUP về thời gian thực thi, bộ nhớ sử dụng và số lượng ứng 
viên sinh ra trong quá trình khai thác. 
 Hướng phát triển tiếp theo là cải tiến cấu trúc dữ liệu lưu trữ để tăng hiệu suất 
thực thi của thuật toán trên các cơ sở dữ liệu dày, khai thác SFUPs trên các dạng cơ sở dữ 
liệu khác như cơ sở dữ liệu tăng trưởng (increamental database), cơ sở dữ liệu động 
(dynamic database). 
 TÀI LIỆU THAM KHẢO 
[1] J. Han, J. Pei, and Y. Yin, “Mining frequent patterns without candidate generation,” 
 ACM Sigmod Record, Vol. 29, No. 2, pp. 1-12, 2000. 
[2] G. Grahne and J. Zhu, “Fast algorithms for frequent itemset mining using FP-
 Trees,” IEEE Transactions on Knowledge and Data Engineering, Vol. 17, No. 10, 
 pp. 1347-1362, 2005. 
[3] B. Vo, T. Le, T. P. Hong, and B. Le, “Fast updated frequent-itemset lattice for 
 transaction deletion,” Data & Knowledge Engineering, Vol. 96, pp. 78-89, 2015. 
[4] Z. H. Deng and S. L. Lv, “Fast mining frequent itemsets using Nodesets,” Expert 
 Systems with Applications, Vol. 41, No. 10, pp. 4505-4512, 2014. 
[5] R. Agrawal and R. Srikant, “Fast algorithms for mining association rules,” In Proc. 
 20th Int. Conf. Very Large Data Bases (VLDB), pp. 487-499, 1994. 
[6] M. Zaki, S. Parthasarathy, M. Ogihara, and W. Li, “New algorithms for fast 
 discovery of association rules,” Knowledge Discovery and Data Mining, pp. 283-
 286, 1997. 
[7] B. Vo, T. P. Hong, and B. Le, “A lattice-based approach for mining most 
 generalization association rules,” Knowledge-Based Systems, Vol. 45, pp. 20-30, 
 2013. 
[8] Y. Liu, W. K. Liao, and A. Choudhary, “A two-phase algorithm for fast discovery of 
 high utility itemsets,” In Pacific-Asia Conference on Knowledge Discovery and 
 Data Mining, pp. 689-695, 2005. 
[9] H. Yao and H. J. Hamilton, “Mining itemsets utilities from transaction databases,” 
 Data and Knowledge Engeneering, Vol. 59, No. 3, pp. 603-626, 2006. 
[10] V. S. Tseng, C. W. Wu, B. E. Shie, and P. S. Yu, “UP-Growth: an efficient 
 algorithm for high utility itemset mining,” In Proceedings of the 16th ACM 
 SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 
 253-262, 2010. 
[11] J. Liu, K. Wang, and B. C. Fung, “Direct discovery of high utility itemsets without 
 candidate generation,” IEEE 12th International Conference on Data Mining, pp. 
 984-989, 2012. 
 79 
 N. T. T. Thủy, M. T. Lý, N. V. Lễ, V. V. Vinh / Một thuật toán hiệu quả để trích xuất tập Skyline 
[12] P. Fournier-Viger, C. W. Wu, S. Zida, and V. S. Tseng, “FHM: Faster high-utility 
 itemset mining using estimated utility co-occurrence pruning,” International 
 Symposium on Methodologies for Intelligent Systems, Vol. 8502, pp. 83-92, 2014. 
[13] G. I. Webb, “Filtered‐top‐k association discovery,” Data Mining and Knowledge 
 Discovery, Vol. 1, No. 3, pp. 183-192, 2011. 
[14] P. Fournier-Viger, C. W. Wu, and V. S. Tseng, “Mining top-k association rules,” 
 Canadian Conference on Artificial Intelligence, pp. 61-73, 2012. 
[15] L. T. Nguyen, B. Vo, L. T. Nguyen, P. Fournier-Viger, and A. Selamat, “ETARM: 
 an efficient top-k association rule mining algorithm,” Applied Intelligence, Vol. 48, 
 No. 5, pp. 1148-1160, 2018. 
[16] V. S. Tseng, C. W. Wu, P. Fournier-Viger, and S. Y. Philip, “Efficient algorithms 
 for mining top-k high utility itemsets,” IEEE Transactions on Knowledge and Data 
 Engineering, Vol. 28, No. 1, pp. 54-67, 2015. 
[17] K. Singh, S. S. Singh, A. Kumar, and B. Biswas, “TKEH: an efficient algorithm for 
 mining top-k high utility itemsets,” Applied Intelligence, Vol. 49, No. 3, pp. 1078-
 1097, 2019. 
[18] S. Krishnamoorthy, “Mining top-k high utility itemsets with effective threshold 
 raising strategies,” Expert Systems with Applications, Vol. 117, pp. 148-165, 2019. 
[19] V. Goyal, A. Sureka, and D. Patel, “Efficient skyline itemsets mining,” The 
 International C* Conference on Computer Science & Software Engineering, pp. 
 119-124, 2015. 
[20] J. S. Pan, J. C. W. Lin, L. Yang, P. Fournier-Viger, and T. P. Hong, “Efficiently 
 mining of skyline frequent-utility patterns,” Intelligent Data Analysis, Vol. 21, No. 
 6, pp. 1407-1423, 2017. 
[21] J.C.W. Lin, L. Yang, P. Fournier-Viger, and T.P. Hong, “Mining of skyline patterns 
 by considering both frequent and utility constraints,” Engineering Applications of 
 Artificial Intelligence, Vol. 77, pp. 229-238, 2019. 
[22] B. Le, H. Nguyen, and B. Vo, “An efficient strategy for mining high utility 
 itemsets,” International Journal of Intelligent Information and Database Systems, 
 Vol.5, No. 2, pp. 164-176, 2011. 
[23] V. S. Tseng, B. E. Shie, C. W. Wu, and S. Y. Philip, “Efficient algorithms for 
 mining high utility itemsets from transactional databases,” IEEE transactions on 
 knowledge and data engineering, Vol.25, pp. 1772-1786, 2012. 
[24] M. Liu and J. Qu, “Mining high utility itemsets without candidate generation,” In 
 Proceedings of the 21st ACM International Conference on Information and 
 Knowledge Management, pp. 55-64, 2012. 
[25] S. Zida, P. Fournier-Viger, J. C. W. Lin, C. W. Wu, and V. S. Tseng, “EFIM: A fast 
 and memory efficient algorithm for high-utility itemset mining,” Knowledge and 
 Information Systems, Vol. 51, No. 2, pp. 595-625, 2017. 
[26] S. Krishnamoorthy, “HMiner: Efficiently mining high utility itemsets,” Expert 
 Systems with Applications, Vol. 90, pp. 168-183, 2017. 
 80 
Trường Đại học Vinh Tạp chí khoa học, Tập 49 - Số 4A/2020, tr. 68-81 
[27] J.S. Yeh, Y. C. Li, and C. C. Chang, “Two-phase algorithms for a novel utility-
 frequent mining model,” International Conference on Emerging Technologies in 
 Knowledge Discovery and Data Mining, pp. 433-444, 2007. 
[28] V. Podpecan, N. Lavrac, and I. Kononenko, “A fast algorithm for mining utility-
 frequent itemsets,” International Workshop on Constraint-based Mining and 
 Learning, pp. 9-20, 2007. 
[29] S. Krishnamoorthy, “Pruning strategies for mining high utility itemsets,” Expert 
 Systems with Applications, Vol. 42, No. 5, pp. 2371-2381, 2015. 
[30] P. Fournier-Viger, A. Gomariz, A. Soltani, and H. Lam, “An Open-Source Data 
 Mining Library,” 2014. [Online].  
[31] R. Agrawal and R. Srikant, “Quest synthetic data generator - IBM Almaden Research 
 Center,” 1994. [Online].  
 SUMMARY 
 AN EFFICIENT ALGORITHM TO EXTRACT SKYLINE ITEMSETS 
 Nguyen Thi Thanh Thuy, Manh Thien Ly, 
 Nguyen Van Le, Vu Van Vinh 
 Ho Chi Minh City University of Food Industry 
 Received on 06/10/2020, accepted for publication on 23/12/2020 
 Mining skyline frequent-utility patterns (SFUPs) is the discovery of itemsets that 
surpasses all other itemsets in both frequency and utility in transactional database. The 
discovery of these itemsets is important for managers in finding items that customers 
buy many times and bring high profits for businesses. In recent years, there have been 
many algorithms proposed to exploit skyline frequent-utility patterns, of which 
SKYFUP-D is the most efficient algorithm. However, this algorithm still has limitations 
in both execution time and storage space. In this paper, we propose an effective method 
to exploit SFUPs faster by applying pruning strategies to reduce the number of 
candidates. Experimental results show that the execution time and storage space are 
significantly improved. 
 Key words: SFUPs; skyline frequent-utility itemset; EUCS; LA. 
 81