Một thuật toán hiệu quả cho bài toán khai thác mẫu tuần tự với ràng buộc trọng số

 là một mẫu tuần tự. Mẫu tuần tự có chiều dài l được 
gọi là l-pattern. 
 Trọng số của item, itemset, sequence [15]: 
 Trọng số (weight) của một item w(i) là một số thực không âm, phản ánh mức độ quan trọng của item 
trong SD. 
 Đặt i là một item đơn (single item), s1, s2, ..., sn là n chuỗi trong SD, trọng số của i được tính như sau: 
 W(i) = (1) 
 ()
 T(i i trong SD, L(s s . 
 Với ) là số lần xuất hiện∑ của  j) là chiều dài của chuỗi j
 Đặt α = là một chuỗi, tk (1 k m) là một thành phần của α, bao gồm n item đơn i1, i2,..., 
in, trọng số của tk được định nghĩa: 
 W(tk) = (2) 
  
 Và trọng số của α là: ∑ ( )
 
 W(α) = (3) 
  
 Trọng số trung bình: ∑ ( )
 
 Đặt SD là một CSDL chuỗi gồm n item đơn ik (1 k n), ta định nghĩa trọng số lớn nhất maxW của 
SD là: maxW = max1 k n (W(ik)) và trọng số nhỏ nhất minW của SD là: minW = min1 k n (W(ik)). Khi 
đó, giá trị trọng số trung bình MeanW của SD được tính như sau: 
 meanW = (maxW + minW) / 2 (4) 
 Item i là một item có trọng số phổ biến nếu support(i) * meanW min_sup 
4 THUẬT TOÁN WPM ĐỂ KHAI THÁC MẪU TUẦN TỰ VỚI RÀNG BUỘC TRỌNG SỐ 
Thuật toán khai thác mẫu tuần tự phổ biến với ràng buộc trọng số gọi là WPM (Weighted Pattern 
Mining) do bài báo đề xuất được trình bày trong hình 1. Thuật toán WPM được xây dựng dựa trên sự kết 
hợp giữa giá trị độ hỗ trợ và trọng số của các item trong CSDL chuỗi để tìm ra tập các mẫu tuần tự có 
trọng số hoàn chỉnh và có giá trị cao. Các trọng số của các item trong thuật toán được tính toán dựa trên 
giá trị thực của item đó trong CSDL thay vì sử dụng một giá trị ước lượng do người dùng đặt. Bên cạnh 
đó, việc khai thác tập mẫu trên CSDL chuỗi trong thuật toán được thực hiện theo hướng tiếp cận cấu trúc 
dữ liệu được tổ chức theo chiều dọc và kết hợp sử dụng khối mã hóa nguyên tố [7] để biểu diễn thông tin 
ứng viên và tính toán độ hỗ trợ của các ứng viên khi phát triển các mẫu giúp nâng cao hiệu suất thực thi 
của phương pháp đề xuất. 
 Không gian tìm kiếm của thuật toán WPM là cây từ điển [2, 7], nghĩa là phát triển mẫu tuần tự phổ 
biến có trọng số theo DFS (Depth First Search). Nút gốc ở mức 0 của cây chứa chuỗi rỗng, các nút ở mức 
tiếp theo của cây gọi là mức thứ l và có kích thước là l. Nút con ở mức (l+1) được xây dựng bằng việc mở 
rộng chuỗi theo mức l và thu được chuỗi có kích thước (l+1), mở rộng mẫu được thực hiện bằng cách 
thêm một item phổ biến vào mẫu với 2 phương pháp là mở rộng mẫu theo chuỗi và mở rộng mẫu theo 
itemset. Thuật toán hoạt động như sau: Đầu vào của thuật toán gồm có một CSDL chuỗi biểu diễn theo 
chiều dọc, một ngưỡng hỗ trợ tối thiểu min_sup. Trước tiên, thuật toán duyệt CSDL đầu vào một lần và 
xác định trọng số của từng item trong CSDL. Từ đó xác định được trọng số lớn nhất và trọng số nhỏ nhất 
để tính được trọng số trung bình meanW từ hai giá trị này theo công thức (4) đã trình bày ở phần 3. Tiếp 
theo, thuật toán sẽ tìm ra tập các item phổ biến có chiều dài là 1 thỏa điều kiện: support (i) * meanW 
min_sup, đồng thời loại bỏ các item không phổ biến ra khỏi F1. Với mỗi item phổ biến i F1, thuật toán 
thực hiện phát triển mẫu theo chuỗi bằng thủ tục S_EXTEND và phát triển mẫu theo itemset bằng thủ tục 
I_EXTEND. Với một mẫu mới được phát sinh, thuật toán tiếp tục gọi đệ quy các thủ tục mở rộng mẫu 
theo chuỗi hay theo itemset để xây dựng không gian các mẫu tuần tự có trọng số theo chiều sâu. Các tham 
số đầu vào ứng với từng thủ tục để phát triển mẫu bao gồm tập Sn chứa các item được nối vào bằng 
© 2020 Trường Đại học Công nghiệp Thành phố Hồ Chí Minh 
 MỘT THUẬT TOÁN HIỆU QUẢ CHO BÀI TOÁN KHAI THÁC MẪU TUẦN TỰ VỚI RÀNG BUỘC TRỌNG SỐ 19 
cách mở rộng theo chuỗi s – extension hoặc mở rộng theo itemset i – extension, min_sup. Với từng ứng 
viên pat được tạo bởi một lần mở rộng mẫu, thuật toán tính lại độ hỗ trợ của mẫu để kiểm tra xem mẫu đó 
có phổ biến hay không theo điều kiện support (α) * meanW min_sup. Việc này được thực hiện bằng 
toán tử kết và tính toán số các chuỗi mà các mẫu có xuất hiện dựa trên phương pháp khối mã hóa nguyên 
tố [7]. Nếu một mẫu là mẫu tuần tự phổ biến có trọng số, mẫu đó sẽ tiếp tục được sử dụng để gọi đệ quy 
hai thủ tục mở rộng mẫu theo chuỗi và theo itemset để tạo ra các mẫu ứng viên bắt đầu với tiền tố . 
Thuật toán cắt tỉa không gian tìm kiếm bằng việc không mở rộng các mẫu không phổ biến. Điều này thực 
hiện được dựa vào tính chất phổ biến của một mẫu tuần tự đó là mẫu tuần tự không phổ biến không thể 
được mở rộng để tạo thành một mẫu phổ biến. 
 WPM (CSDL, min_sup) 
 1. Duyệt CSDL để xác định meanW và F1: danh sách các item phổ biến thỏa điều kiện support (i) 
 * meanW min_sup 
 2. pat_weight := 
 3. FOREACH item i F1, 
 4. S_EXTEND (, F1, min_sup) 
 5. I_EXTEND (, {e F1 | e lex i}, min_sup) 
 S_EXTEND (pat, Sn, min_sup) ≻
 1. pat_weight  pat; 
 2. Stemp := 
 3. FOREACH item j Sn, 
 4. pnew = s_extension(pat, j); 
 5. IF support(pnew)*meanW ≥ min_sup 
 6. THEN Stemp := Stemp  (j) 
 7. FOREACH item j Stemp, 
 8. S_EXTEND (pnew, Stemp, min_sup) 
 I_EXTEND (pat, In, min_sup) 
 1. pat_weight  pat; 
 2. Itemp := 
 3. FOREACH item j In, 
 4. pnew = i_extension(pat, j); 
 5. IF support(pnew)*meanW ≥ min_sup 
 6. THEN Itemp := Itemp  (j) 
 7. FOREACH item j Itemp, 
 8. I_EXTEND (pnew, {e Itemp| e lex j}, min_sup) 
 Hình 1: Thuật toán WPM để khai thác≻ mẫu tuần tự với ràng buộc trọng số 
5 KẾT QUẢ THỰC NGHIỆM 
Kết quả thực nghiệm của thuật toán WPM để khai thác mẫu tuần tự với ràng buộc trọng số mà bài báo đề 
xuất được so sánh với thuật toán SPMW [15]. Các kết quả thực nghiệm được thực hiện trên máy tính Intel 
(R), Core (TM) i3-2370M CPU 2.40 GHz, 4Gb RAM trên hệ điều hành Windows 10 với ngôn ngữ lập 
trình Java trên nền tảng Eclipse. CSDLsử dụng trong thực nghiệm là các bộ dữ liệu chuẩn được tải trực 
tiếp từ  Đây là địa chỉ chứa các tập dữ liệu tin cậy được cộng đồng nghiên cứu 
khai thác mẫu tuần tự sử dụng để kiểm chứng thực nghiệm các thuật toán đề xuất. Đặc điểm của các bộ 
dữ liệu sử dụng trong thực nghiệm được trình bày trong bảng 1. 
 Bảng 1: Đặc điểm của các bộ CSDL chuẩn 
 CSDL Số chuỗi Số item phân biệt Số itemset trung bình/chuỗi 
 Sign 730 267 51 
 Chess 3196 75 37 
 Mushroom 8124 119 23 
 T40I10D100k 100000 942 39 
 © 2020 Trường Đại học Công nghiệp thành phố Hồ Chí Minh 
20 MỘT THUẬT TOÁN HIỆU QUẢ CHO BÀI TOÁN KHAI THÁC MẪU TUẦN TỰ VỚI RÀNG BUỘC TRỌNG SỐ 
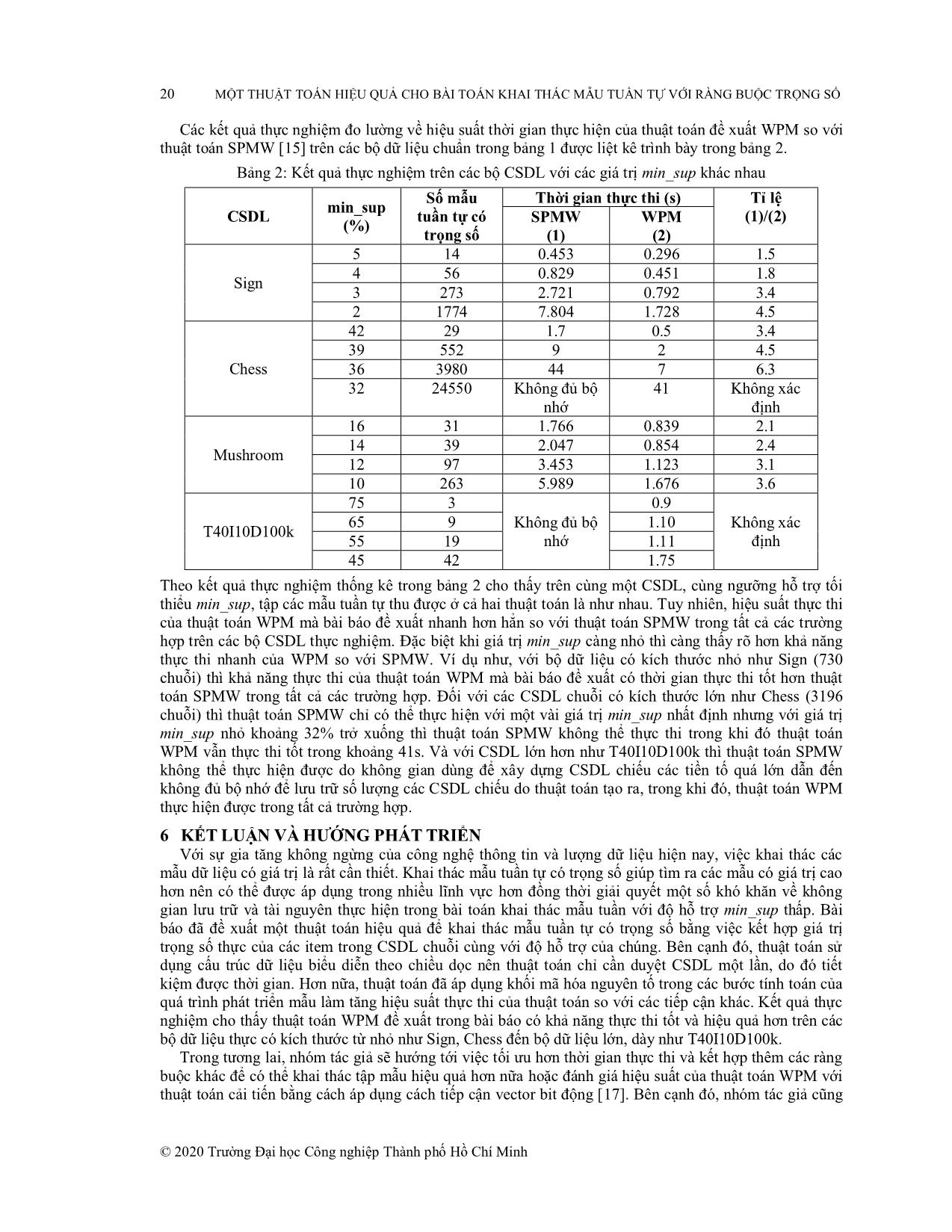
 Các kết quả thực nghiệm đo lường về hiệu suất thời gian thực hiện của thuật toán đề xuất WPM so với 
thuật toán SPMW [15] trên các bộ dữ liệu chuẩn trong bảng 1 được liệt kê trình bày trong bảng 2. 
 Bảng 2: Kết quả thực nghiệm trên các bộ CSDL với các giá trị min_sup khác nhau 
 Thời gian thực thi (s) Tỉ lệ 
 min_sup Số mẫu 
 CSDL SPMW WPM (1)/(2) 
 (%) tuần tự có 
 trọng số (1) (2) 
 5 14 0.453 0.296 1.5 
 4 56 0.829 0.451 1.8 
 Sign 
 3 273 2.721 0.792 3.4 
 2 1774 7.804 1.728 4.5 
 42 29 1.7 0.5 3.4 
 39 552 9 2 4.5 
 Chess 36 3980 44 7 6.3 
 32 24550 Không đủ bộ 41 Không xác 
 nhớ định 
 16 31 1.766 0.839 2.1 
 14 39 2.047 0.854 2.4 
 Mushroom 
 12 97 3.453 1.123 3.1 
 10 263 5.989 1.676 3.6 
 75 3 0.9 
 65 9 1.10 Không xác 
 T40I10D100k Không đủ bộ 
 55 19 nhớ 1.11 định 
 45 42 1.75 
Theo kết quả thực nghiệm thống kê trong bảng 2 cho thấy trên cùng một CSDL, cùng ngưỡng hỗ trợ tối 
thiểu min_sup, tập các mẫu tuần tự thu được ở cả hai thuật toán là như nhau. Tuy nhiên, hiệu suất thực thi 
của thuật toán WPM mà bài báo đề xuất nhanh hơn hẳn so với thuật toán SPMW trong tất cả các trường 
hợp trên các bộ CSDL thực nghiệm. Đặc biệt khi giá trị min_sup càng nhỏ thì càng thấy rõ hơn khả năng 
thực thi nhanh của WPM so với SPMW. Ví dụ như, với bộ dữ liệu có kích thước nhỏ như Sign (730 
chuỗi) thì khả năng thực thi của thuật toán WPM mà bài báo đề xuất có thời gian thực thi tốt hơn thuật 
toán SPMW trong tất cả các trường hợp. Đối với các CSDL chuỗi có kích thước lớn như Chess (3196 
chuỗi) thì thuật toán SPMW chỉ có thể thực hiện với một vài giá trị min_sup nhất định nhưng với giá trị 
min_sup nhỏ khoảng 32% trở xuống thì thuật toán SPMW không thể thực thi trong khi đó thuật toán 
WPM vẫn thực thi tốt trong khoảng 41s. Và với CSDL lớn hơn như T40I10D100k thì thuật toán SPMW 
không thể thực hiện được do không gian dùng để xây dựng CSDL chiếu các tiền tố quá lớn dẫn đến 
không đủ bộ nhớ để lưu trữ số lượng các CSDL chiếu do thuật toán tạo ra, trong khi đó, thuật toán WPM 
thực hiện được trong tất cả trường hợp. 
6 KẾT LUẬN VÀ HƯỚNG PHÁT TRIỂN 
 Với sự gia tăng không ngừng của công nghệ thông tin và lượng dữ liệu hiện nay, việc khai thác các 
mẫu dữ liệu có giá trị là rất cần thiết. Khai thác mẫu tuần tự có trọng số giúp tìm ra các mẫu có giá trị cao 
hơn nên có thể được áp dụng trong nhiều lĩnh vực hơn đồng thời giải quyết một số khó khăn về không 
gian lưu trữ và tài nguyên thực hiện trong bài toán khai thác mẫu tuần với độ hỗ trợ min_sup thấp. Bài 
báo đã đề xuất một thuật toán hiệu quả để khai thác mẫu tuần tự có trọng số bằng việc kết hợp giá trị 
trọng số thực của các item trong CSDL chuỗi cùng với độ hỗ trợ của chúng. Bên cạnh đó, thuật toán sử 
dụng cấu trúc dữ liệu biểu diễn theo chiều dọc nên thuật toán chỉ cần duyệt CSDL một lần, do đó tiết 
kiệm được thời gian. Hơn nữa, thuật toán đã áp dụng khối mã hóa nguyên tố trong các bước tính toán của 
quá trình phát triển mẫu làm tăng hiệu suất thực thi của thuật toán so với các tiếp cận khác. Kết quả thực 
nghiệm cho thấy thuật toán WPM đề xuất trong bài báo có khả năng thực thi tốt và hiệu quả hơn trên các 
bộ dữ liệu thực có kích thước từ nhỏ như Sign, Chess đến bộ dữ liệu lớn, dày như T40I10D100k. 
 Trong tương lai, nhóm tác giả sẽ hướng tới việc tối ưu hơn thời gian thực thi và kết hợp thêm các ràng 
buộc khác để có thể khai thác tập mẫu hiệu quả hơn nữa hoặc đánh giá hiệu suất của thuật toán WPM với 
thuật toán cải tiến bằng cách áp dụng cách tiếp cận vector bit động [17]. Bên cạnh đó, nhóm tác giả cũng 
© 2020 Trường Đại học Công nghiệp Thành phố Hồ Chí Minh 
 MỘT THUẬT TOÁN HIỆU QUẢ CHO BÀI TOÁN KHAI THÁC MẪU TUẦN TỰ VỚI RÀNG BUỘC TRỌNG SỐ 21 
hướng đến việc phát triển các thuật toán khai thác tập top-k mẫu tuần tự có trọng số với dữ liệu chuỗi ở 
một số lĩnh vực cụ thể như chuỗi dữ liệu giao dịch, chuỗi dữ liệu khách hàng, chuỗi lịch sử truy cập web, 
LỜI CẢM ƠN 
Bài báo được thực hiện với sự hỗ trợ từ quỹ đề tài nghiên cứu khoa học của trường đại học Công nghiệp 
TP HCM, mã số 20/1.6CNTT01 
TÀI LIỆU THAM KHẢO 
[1]. R. Agrawal, R. Srikant. Mining sequential patterns, Proceedings of the 11th International 
Conference on Data Engineering, pp. 3–14, 1995. 
[2]. J. Ayres, J.E. Gehrke, T. Yiu, J. Flannick. Sequential pattern mining using a bitmap 
representation, Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and 
Data Mining, pp. 429–435, 2002. 
[3]. V. Chezhian V. Umadevi, J. Celin, S. Geetha. Hierarchical sequence clustering algorithm fordata 
 mining, Proceedings of the World Congress on Engineering, pp. 21 – 25, 2011. 
[4]. P. Fournier-Viger, A. Gomariz, M. Campos, R. Thomas. Fast vertical mining of sequential 
patterns using co-occurrence information. In: PAKDD’14, pp. 40–52, 2014. 
[5]. W. Gan, J. C.-W. Lin, P. Fournier-Viger, H.-C. Chao, P. S. Yu. A Survey of Parallel Sequential 
Pattern Mining, ACM Transactions on Knowledge Discovery from Data, vol. 13, no. 3, 2019. 
[6]. M. N. Garofalakis, R. Rastogi, K. Shim. SPIRIT: Sequential Pattern Mining with Regular 
Expression Constraints, Proc. of the Very Large Data Bases Conf., Edinburgh, Scotland, UK, pp. 223-
234, 1999. 
[7]. K. Gouda, M. Hassaan, M.J. Zaki. PRISM: a primal-encoding approach for frequent sequence 
mining, Journal of Computer and System Sciences, vol. 76, no. 1, pp. 88–102, 2010. 
[8]. J. Han, J. Pei, B. Mortazavi-Asl, Q. Chen, U. Dayal, M. C. Hsu. Freespan: Frequent pattern-
projected sequential pattern mining, Proceedings of the sixth ACM SIGKDD international conference on 
Knowledge discovery and data mining, pp. 355-359, 2000. 
[9]. J. Han, M. Kamber. Data Mining: Concepts and Techniques 3nd Edition. Morgan Kanufmann, 
2012. 
[10]. B. Huynh, B. Vo, V. Snasel. An efcient method for mining frequent sequential patterns using 
multi-core processors, Applied Intelligence, vol. 46, no. 3, pp. 703–716, 2017. 
[11]. B. Huynh, C. Trinh, H. Huynh, T.T. Van, B. Vo, V. Snasel. An efficient approach for mining 
sequential patterns using multiple threads on very large databases, Engineering Applications of Artificial 
Intelligence, vol. 74, pp. 242–251, 2018. 
[12]. F. Masseglia, F. Cathala, P. Poncelet. The PSP Approach for Mining Sequential Patterns, 
Proceedings of the 2nd European Symposium on Principles of Data Mining and Knowledge Discovery, 
Nantes, France, pp. 176-184, 1998. 
 © 2020 Trường Đại học Công nghiệp thành phố Hồ Chí Minh 
22 MỘT THUẬT TOÁN HIỆU QUẢ CHO BÀI TOÁN KHAI THÁC MẪU TUẦN TỰ VỚI RÀNG BUỘC TRỌNG SỐ 
[13]. J. Pei, J. Han, B. Mortazavi-Asl, J. Wang, H. Pinto, Q. Chen, U. Dayal, M. C. Hsu. Mining 
sequential patterns by pattern-growth: the prefixspan approach, IEEE 
Transactions on Knowledge and Data Engineering, vol. 16, no. 11, pp. 1424–1440, 2004. 
[14]. B. Shim, K. Choi, Y. Suh. CRM strategies for a small-sized online shopping mall based on 
association rules and sequential patterns, Expert Systems with Applications, vol. 39, pp. 7736 – 7742, 
2012. 
[15]. A. Sirisha, S. Pabboju, G. Narsimha. Efficient mining of sequential patterns in a sequence 
database with weight constraint, International Journal on Recent and Innovation Trends in Computing 
and Communication, vol. 4, no. 6, pp. 394 – 397, 2016. 
[16]. R. Srikant, R. Agrawal. Mining sequential patterns: Generalizations and performance 
improvements, In: 5th Intl. Conf. Extending Database Technology, pp. 3 – 17, 1996. 
[17]. T. Van, B. Vo, B. Le. Mining sequential patterns with itemset constraints, Knowledge and 
Information Systems, vol. 57, no. 2, pp. 311-330, 2018. 
[18]. W. Wang, J. Yang. Mining Sequential Patterns From Large Data Sets, Springer, 2005. 
[19]. U. Yun, J. Leggett. WFIM: Weighted frequent itemset mining with a weight range and a 
 minimum weight, In: Fourth SIAM Int. Conf. on Data Mining, USA, pp. 636–640, 2005. 
[20]. U. Yun, J. Leggett. WSpan: Weighted sequential pattern mining in large sequence databases, 3rd 
International IEEE Conference on Intelligent Systems, pp. 512 – 517, 2006. 
[21]. U. Yun. A new framework for detecting weighted sequential patterns in large sequence databases, 
Knowledge – base systems, vol. 21, pp. 110 – 122, 2008. 
[22]. M.J. Zaki. SPADE: an efficient algorithm for mining frequent sequences, The Journal of 
Machine Learning Research, vol. 42, pp. 31–60, 2001. 
 Ngày nhận bài: 02/10/2019 
 Ngày chấp nhận đăng: 09/01/2020 
© 2020 Trường Đại học Công nghiệp Thành phố Hồ Chí Minh