Một phương pháp tính toán tương quan giữa xung nhịp máy và phép cộng hai số nguyên khi thực hiện trên phần cứng

i A và C trước và sau một nhịp máy nào đó thì 
 C "[0] 0
 C"[ i ] A '[ i 1] C '[ i 1] (0 i m ) (2.4) 
 A"[ i ] A '[ i ]  C '[ i ] (0 i m )
2.2. Phân phối xác suất của đại lượng F(k) 
Tính chất: F(k) là một đại lượng ngẫu nhiên nhận giá trị nguyên từ 0 đến k+1 có 
phân bố 
 Prob(F(k)=f) = N(k,f ) (f=0, 1, ..., k+1). (2.5) 
 4k
trong đó, N(k,f) = #{(X,Y): X, Y [0, 2k) và flops(X,Y) = f}. 
Chứng minh: Với Y = 0 thì trạng thái của thanh ghi C có giá trị tất cả các bít bằng 
0 vì vậy mạch dừng và điều này có nghĩa 
 flops(X,0) = 0. (2.6) 
Với mọi f = 1, 2, ..., k+1; lấy X = 1 và Y = 2f 1 1 thì trạng thái đầu tiên của C là 
có đúng f 1 bít 1 từ các vị trí thấp nhất còn của A chỉ có đúng một bít 1 ở vị trí 
thấp nhất. Dễ dàng nhận ra rằng 
 flops(1, 2f 1 1) = f (f = 1, 2, ..., k+1). (2.7) 
Bây giờ ta sẽ chứng tỏ với mọi X, Y [0, 2k) thì 
 flops(X,Y) k+1. (2.8) 
 Thật vậy, từ X, Y < 2k nên X + Y < 2k+1 vì vậy trong suốt quá trình thực hiện 
của mạch cộng thanh ghi C có các bít 1 chỉ xuất hiện ở k+1 vị trí thấp nhất. Theo 
công thức (2.4) thì sau mỗi nhịp máy thì số bít thấp nhất bằng 0 của C sẽ tăng thêm 
1 (do phép dịch trái 1 vị trí) cho nên nhiều nhất là k+1 nhịp thì C sẽ không còn bít 
1 và đương nhiên phép cộng đã hoàn thành. Như vậy, các kết quả (2.6), (2.7) và 
(2.8) đã chứng minh tính đúng đắn của tính chất. Từ X, Y [0, 2k) nên ta có 2k 2k 
= 4k cặp (X,Y) khác nhau và từ định nghĩa của giá trị N(k,f) ta có ngay (2.5) và 
tính chất đã được chứng minh. 
2.3. Cách tiếp cận và công cụ để tính giá trị AAF(k) 
 Để tính AAF(k) có hai tiếp cận để thực hiện đó là tính đúng giá trị này trong 
trường hợp k<15 và tính gần đúng nó trong trường hợp ngược lại. 
2.3.1. Công thức tính đúng giá trị AAF(k) 
 Theo công thức (2.5) ta có công thức sau để tính đúng giá trị AAF(k): 
Công thức tính đúng giá trị AAF(k) 
 Total() k
 AAF(k) = (2.9) 
 4k
76 L. §. T©n, H. V. Qu©n, H. N. Minh, " Mét ph­¬ng ph¸p tÝnh to¸n ... trªn phÇn cøng." 
Nghiªn cøu khoa häc c«ng nghÖ 
 trong đó Total k  flops(,) x y là tổng số nhịp máy cần thiết để thực hiện 
 x, y [0,2k )
toàn bộ 4k phép cộng các số nguyên trong miền [0, 2k). 
 k 1 N(,) k f 1 k 1 Total (k)
Thật vậy, AAF(k)= E(F(k))  j = j N (k, f ) = . Như 
 k k  k
 j 0 4 4 j 0 4
vậy công thức (2.9) đã được chứng minh. 
2.3.2. Công thức tính gần đúng giá trị AAF(k) 
 Theo [1] khi khảo sát một đại lượng ngẫu nhiên X nào đó người ta tiến hành M 
phép thử (quan sát giá trị nhận được của X), giả sử trong phép thử thứ i, giá trị 
 M
nhận được của X là xi (i=1, ..., M). Khi này (1/M ) xi được gọi là kỳ vọng mẫu, 
 i 1
M được gọi là kích thước mẫu và như một hệ quả của định lý Markov ta có với 
mọi >0 nhỏ tùy ý thì 
 1 M = 1 (2.10) 
 lim Prob  xi E ( X )  
 M M i 1 
Áp dụng cho X=F(k) ta có 
 1 M = 1 (2.11) 
 lim Prob  Fi ( k ) AAF ( k )  
 M M i 1 
 M
Từ (2.11) thì ta có thể lấy (1/M ) Fi ( k ) là giá trị gần đúng của AAF(k) và chứng 
 i 1
minh tương tự như cho công thức (2.9) ta có công thức tính gần đúng giá trị 
AAF(k) 
 AAF(k) Total(,) k M (2.12) 
 M
trong đó, Total(k,M)=  flops(,) x y là tổng số nhịp máy cần thiết để thực hiện 
 i 1.. M i i
M phép cộng các số nguyên được lấy một cách ngẫu nhiên trong miền [0, 2k). 
 Total(,) k M 1 M
Biểu thức vế phải =  F() k trong công thức (2.12) được ký hiệu là 
 M M i 1 i
AAF(k,M). 
2.4. Đánh giá |AAF(k) AAF(k,M)| 
2.4.1. Cơ sở lý thuyết 
 Trong [1] cho biết với M khá lớn ta có thể sử dụng công thức đánh giá sau: 
 Prob X E ( X ) t D ( X ) = 2(t). (2.13) 
 M
trong đó XX  / M với Xi là các đại lượng cùng phân phối và độc lập với nhau. 
 i 1 i
Theo tính chất của kỳ vọng và phương sai ta có: E( X )=m ; D( X ) =  2 M 
 Nên (2.13) trở thành 
  = 2(t). (2.14) 
 Pr ob X m t 
 M 
T¹p chÝ Nghiªn cøu KH&CN qu©n sù, Sè 33, 10 - 2014 77 
 Kỹ thuật điện tử & Khoa học máy tính 
 Đại lượng F(k) chỉ nhận hữu hạn giá trị do đó kỳ vọng AAF(k) và phương sai 
của nó, ký hiệu là (k)2, đều hữu hạn dó đó theo công thức (2.14) ta có công thức 
đánh giá tương ứng đó là: 
  ()k 
 Prob AAF ( k , M ) AAF ( k ) t = 2 (t). (2.15) 
 M 
Ví dụ 1: Với t = 3.1, giá trị (3.1) tra được trong bảng 1A (trang 72 [5]) (chú ý: 
với cùng một ký hiệu (t) nhưng trong tài liệu [5] chính là 2 (t) trong [1] là 
0.999032 và điều này có nghĩa nếu lấy (k)= 3.1/M  ( k ) thì theo công thức 
(2.15) ta có ProbAAFkM ( , ) AAFk ( ) ( k ) = 0.9990322. 
2.4.2 Ước lượng giá trị (k) 
 Để áp dụng được công thức (2.15) việc quan trọng tiếp theo là xác định được 
giá trị (k). Trong điều kiện F(k) chưa biết phân bố nên chúng ta chỉ có thể ước 
lượng giá trị (k), mà điều cần thiết để ước lượng là một cận trên của nó. Trong 
mục này chúng ta sẽ đưa ra cách ước lượng nói trên, chúng ta cần chứng minh một 
bổ đề sau: 
Bổ đề: Cho sự kiện ngẫu nhiên A có phân phối xác xuất Prob(A)=p, nếu trong M 
phép thử độc lập ta thấy sự kiện này xuất hiện đúng M lần thì với mọi >0 cho 
trước ta có 
 M 1
 Prob(1 p > ) = 1  (2.16) 
Chứng minh: Biết rằng xác suất để sự kiện A xuất hiện M lần trong M phép thử là 
pM , do đó, 
 1  MM 1 M 1
 Prob(1 p > ) = p dp/ p dp = 1  . 
 0 0
Ví dụ 2. Với M=107 và =0.0000006908 ta có 1  M 1= 0.001. 
 Từ bổ đề trên ta dễ dàng thu được kết quả sau dùng để ước lượng cận trên cho 
giá trị . 
Hệ quả: Cho đại lượng ngẫu nhiên X có miền giá trị là {0, 1, ..., n}. Nếu thực hiện 
 s e n 
M phép thử độc lập X chỉ nhận giá trị trong miền [s,e] và E(X) min ;  . 
 2 2 
Khi đó với mọi 0<<1 ta đánh giá 
 2 2
 2 (1  ) e (1  ) s  n (1  ) s . (2.17) 
Thì xác suất sai lầm loại 2 của đánh giá trên là  = 1  M 1. 
 3. KẾT QUẢ TÍNH TOÁN SỐ AAF(k) VÀ AAF(k,M) 
3.1. Cách tính giá trị AAF(k) 
 Chúng ta sử dụng hàm flops(X,Y) để tính số nhịp máy. Trong trường hợp k 
nhỏ, cụ thể k 14, và tiến hành đếm toàn bộ số nhịp máy cho tất cả 22k phép cộng, 
giá trị thu được ký hiệu là Total(k) và khi này ta có 
 AAF(k) = Total(k) 2 2k. (3.1) 
 Ngược lại, chọn phương pháp thống kê đó là tiến hành lấy ngẫu nhiên M=107 
78 L. §. T©n, H. V. Qu©n, H. N. Minh, " Mét ph­¬ng ph¸p tÝnh to¸n ... trªn phÇn cøng." 
Nghiªn cøu khoa häc c«ng nghÖ 
cặp số nguyên X, Y [0, 2k), tính Total(k,107) tổng của 107 giá trị flops(X,Y) 
trong mỗi lần lấy ngẫu nhiên đó và khi này 
 AAF(k,107) = Total(k,107) 10 7 (3.2) 
 Để phục vụ cho việc đánh giá sai số như đã đưa ra trong mục 2.4, ngoài việc 
tính Total(k) chúng ta còn phải xác định hai tham số fs(k) và fe(k) (dùng trong công 
thức 3.3) với fs(k) là giá trị đầu tiên và fe(k) là giá trị cuối cùng có N(k,f) 0. 
3.2. Kết quả duyệt toàn bộ 22k phép cộng khác nhau với k từ 0 đến 14 
 Total(1) = 3, AAF(1) = 0.750000 
 Total(2) = 21, AAF(2)= 1.312500 
 Total(3) = 113, AAF(3)= 1.765625 
 Total(4) = 547, AAF(4)= 2.136719 
 Total(5) = 2509, AAF(5)= 2.450195 
 Total(6) = 11135, AAF(6)= 2.718506 
 Total(7) = 48373, AAF(7)= 2.952454 
 Total(8) = 206991, AAF(8)= 3.158432 
 Total(9) = 876061, AAF(9) =3.341908 
 Total(10)=3677047, AAF(10)=3.506705 
 Total(11)=15334149, AAF(11)=3.655946 
 Total(12)=63619791, AAF(12)=3.792035 
 Total(13)=262861101, AAF(13)=3.91693 
 Total(14)=1082389767, AAF(14)=4.032216 
3.3. Kết quả thống kê với 107 mẫu cho mỗi k từ 15 đến 4096 
 Bảng 3.1 dưới đây ghi kết quả thống kê được của 112 giá trị k bao gồm k từ 15 
đến 64; k từ 96 đến 1024 trong dạng k=32 i (i=1,..., 30); k từ 1088 đến 2048 trong 
dạng k=64 i (i=1,..., 16) và ; k từ 2176 đến 4096 trong dạng k=128 i (i=1,..., 16). 
 7
Các số liệu được ghi trong bảng bao gồm: k, AAF(k,10 ), fs(k), fe(k) và (k). 
 7
 Các số liệu AAF(k,10 ), fs(k), fe(k) có được từ thống kê còn (k) được ước 
lượng theo ví dụ 1 mục 2.4.1 (để đạt được độ tin cậy 0.999032), giá trị 2 được 
đánh giá theo công thức (2.17) còn  = 0.0000006908 được lấy theo ví dụ 2 mục 
2.4.2 (để đảm bảo xác suất sai không quá 0.001). Tóm lại (k) được tính theo công 
thức sau 
 2 2
 (k) = (1  )(fe (1  ) f s )  ( k 1 (1  ) f s ) (3.3) 
 3.1 7
 10
 Bảng 3.1. Kết quả thống kê 112 giá trị của k. 
 7 7
 k AAF(k,10 ) fs (k) fe (k) (k) k AAF (k,10 ) fs(k) fe (k) (k) 
 15 4.1399501 0 16 0.016039 288 8.4977167 4 30 0.026065 
 16 4.2386532 0 17 0.017042 320 8.6502339 4 34 0.030074 
 17 4.3320945 0 18 0.018044 352 8.7886398 4 33 0.029072 
 18 4.4200825 0 19 0.019046 384 8.9146046 4 31 0.027068 
 19 4.5026766 0 20 0.020049 416 9.0295142 4 31 0.027068 
 20 4.5807384 0 21 0.021051 448 9.1369311 5 30 0.025064 
 21 4.6553482 0 22 0.022054 480 9.2362259 5 31 0.026067 
 22 4.7249131 0 23 0.023056 512 9.3298887 5 31 0.026067 
 23 4.7923977 1 23 0.022054 544 9.4175886 5 30 0.025065 
 24 4.8568043 0 24 0.024059 576 9.5004907 5 32 0.027070 
 25 4.9183709 1 23 0.022054 608 9.5784751 5 33 0.028073 
 26 4.9770195 1 24 0.023056 640 9.6527988 5 32 0.027071 
 27 5.0349873 1 25 0.024059 672 9.7229998 5 34 0.029076 
 28 5.0876514 1 24 0.023056 704 9.7910969 5 31 0.026070 
 29 5.1409723 1 25 0.024059 736 9.8535831 5 34 0.029077 
 30 5.1919811 1 24 0.023056 768 9.9160444 5 34 0.029078 
T¹p chÝ Nghiªn cøu KH&CN qu©n sù, Sè 33, 10 - 2014 79 
 Kỹ thuật điện tử & Khoa học máy tính 
 31 5.2410299 1 26 0.025061 800 9.9746949 5 33 0.028076 
 32 5.2881423 1 27 0.026063 832 10.0314707 5 33 0.028077 
 33 5.3332005 1 25 0.024059 864 10.0860103 6 31 0.025071 
 34 5.3778501 1 25 0.024059 896 10.1386865 5 32 0.027076 
 35 5.4209489 1 28 0.027066 928 10.1888623 5 34 0.029081 
 36 5.4637941 1 27 0.026064 960 10.2389178 6 35 0.029082 
 37 5.5035587 1 26 0.025061 992 10.2861217 5 32 0.027078 
 38 5.5434711 1 27 0.026064 1024 10.3310832 5 34 0.029083 
 39 5.5817211 1 26 0.025061 1088 10.4188155 6 33 0.027081 
 40 5.6189158 1 26 0.025061 1152 10.5008227 6 35 0.029087 
 41 5.6558295 1 26 0.025061 1216 10.5797636 6 34 0.028086 
 42 5.6920440 1 28 0.027066 1280 10.6537093 6 32 0.026085 
 43 5.7259800 1 27 0.026064 1344 10.7234819 6 33 0.027089 
 44 5.7601316 1 31 0.030073 1408 10.7905204 6 34 0.028093 
 45 5.7937005 1 27 0.026064 1472 10.8558274 6 34 0.028095 
 46 5.8254527 1 27 0.026064 1536 10.9169641 6 35 0.029099 
 47 5.8576532 1 26 0.025061 1600 10.9755471 6 33 0.027099 
 48 5.8874458 1 29 0.028068 1664 11.0313155 6 34 0.028102 
 49 5.9189435 1 28 0.027066 1728 11.0867588 6 34 0.028105 
 50 5.9480496 1 27 0.026064 1792 11.1397614 6 33 0.027107 
 51 5.9780568 1 33 0.032078 1856 11.1900650 6 32 0.026109 
 52 6.0063450 1 27 0.026064 1920 11.2385736 7 32 0.025112 
 53 6.0338280 1 26 0.025061 1984 11.2870085 7 30 0.023115 
 54 6.0620954 1 27 0.026064 2048 11.3325767 6 33 0.027119 
 55 6.0884972 1 29 0.028068 2176 11.4198410 7 32 0.025126 
 56 6.1156798 2 28 0.026064 2304 11.5021737 7 32 0.025134 
 57 6.1410676 2 28 0.026064 2432 11.5800870 7 35 0.028141 
 58 6.1666951 1 33 0.032078 2560 11.6550679 7 35 0.028149 
 59 6.1914261 2 27 0.025061 2688 11.7249838 7 35 0.028157 
 60 6.2161775 1 28 0.027066 2816 11.7917189 7 34 0.027167 
 61 6.2402992 2 33 0.031076 2944 11.8547999 7 33 0.026178 
 62 6.2647414 2 29 0.027066 3072 11.9175576 7 33 0.026188 
 63 6.2882122 2 29 0.027066 3200 11.9760081 7 31 0.024205 
 64 6.3104244 2 27 0.025061 3328 12.0320870 7 35 0.028205 
 96 6.9032910 2 29 0.027066 3456 12.0871429 7 32 0.025225 
 128 7.3216611 3 29 0.026064 3584 12.1393587 7 35 0.028226 
 160 7.6464142 3 29 0.026064 3712 12.1904356 7 33 0.026246 
 192 7.9104545 3 28 0.025062 3840 12.2395965 7 34 0.027254 
 224 8.1340866 3 29 0.026064 3968 12.2859574 7 33 0.026272 
 256 8.3274409 4 30 0.026064 4096 12.3345439 8 32 0.024299 
3.4. Đánh giá về hàm AAF(k) 
Kết quả 1: Trong phạm vi k từ 1 đến 4096 ta có bất đẳng thức sau với xác suất tin 
cậy trên 0.998 
 log2(k)  AAF(k)  log2(k)+1. (3.4) 
Chứng minh: Như đã được đánh giá trong ví dụ 1 mục 2.4 thì 
 |AAF(k) AAF(k,M)| < (3.1/M ) ( k ) (3.5) 
với 2(k) là phương sai của F(k) có xác suất tin cậy là 0.9990322 hay nói một cách 
khác là xác suất sai của bất đẳng thức (3.5) là không đến 0.001. Mặt khác theo bất 
đẳng thức (2.17) trong hệ quả trong mục 2.4.2 thì 
 2 (1 ) e (1 ) s 2  n (1 ) s 2 (3.6) 
Ví dụ 2 mục 2.4.2 cho thấy xác suất sai của bất đẳng thức trên trong trường hợp 
M=107 và =0.0000006908 là 0.001. 
Cho nên xác định giá trị (k) theo công thức (3.3) ta có (k) 3.1/M  ( k ) 
và vì thế ta thu được 
 AAF(k,107) (k) AAF(k) AAF(k,107)+ (k) (3.7) 
Với xác suất sai không đến 0.002 và do vậy xác suất tin cậy của (3.7) là trên 0.998. 
 Từ số liệu thống kê về các giá trị AAF(k,107) và (k) tính được đưa ra trong 
bảng 1 ta có ngay được kết quả 1, tuy nhiên để dễ quan sát hơn chúng tôi đã thực 
hiện vẽ 4 đồ thị của các hàm AAF(k,107) (k), ký hiệu là AAF- , 
80 L. §. T©n, H. V. Qu©n, H. N. Minh, " Mét ph­¬ng ph¸p tÝnh to¸n ... trªn phÇn cøng." 
Nghiªn cøu khoa häc c«ng nghÖ 
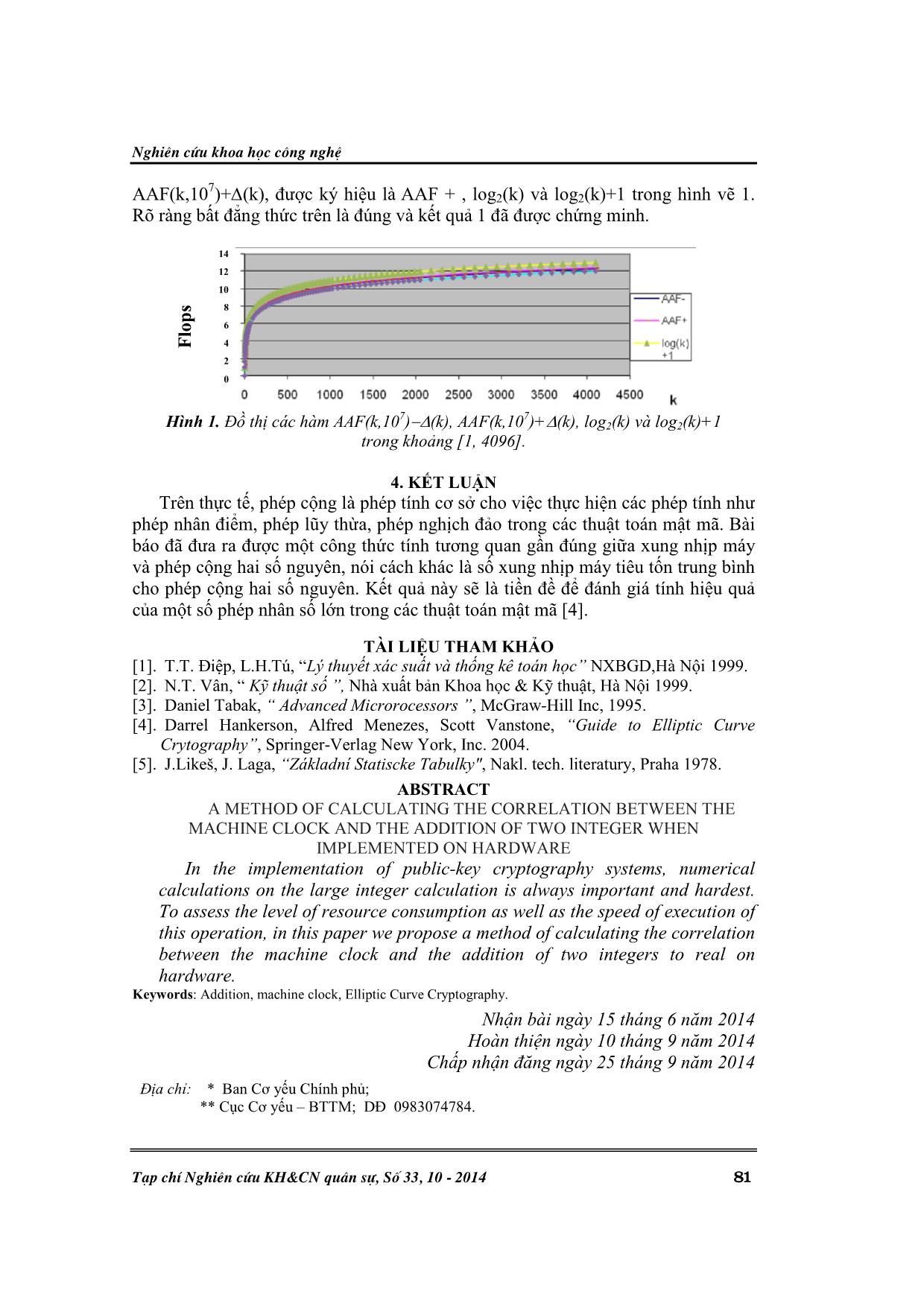
 7
AAF(k,10 )+ (k), được ký hiệu là AAF + , log2(k) và log2(k)+1 trong hình vẽ 1. 
Rõ ràng bất đẳng thức trên là đúng và kết quả 1 đã được chứng minh. 
 14 
 12 
 10 
 8 
 6 
 Flops 4 
 2 
 0 
 7 7
 Hình 1. Đồ thị các hàm AAF(k,10 ) (k), AAF(k,10 )+ (k), log2(k) và log2(k)+1 
 trong khoảng [1, 4096]. 
 4. KẾT LUẬN 
 Trên thực tế, phép cộng là phép tính cơ sở cho việc thực hiện các phép tính như 
phép nhân điểm, phép lũy thừa, phép nghịch đảo trong các thuật toán mật mã. Bài 
báo đã đưa ra được một công thức tính tương quan gần đúng giữa xung nhịp máy 
và phép cộng hai số nguyên, nói cách khác là số xung nhịp máy tiêu tốn trung bình 
cho phép cộng hai số nguyên. Kết quả này sẽ là tiền đề để đánh giá tính hiệu quả 
của một số phép nhân số lớn trong các thuật toán mật mã [4]. 
 TÀI LIỆU THAM KHẢO 
[1]. T.T. Điệp, L.H.Tú, “Lý thuyết xác suất và thống kê toán học” NXBGD,Hà Nội 1999. 
[2]. N.T. Vân, “ Kỹ thuật số ”, Nhà xuất bản Khoa học & Kỹ thuật, Hà Nội 1999. 
[3]. Daniel Tabak, “ Advanced Microrocessors ”, McGraw-Hill Inc, 1995. 
[4]. Darrel Hankerson, Alfred Menezes, Scott Vanstone, “Guide to Elliptic Curve 
 Crytography”, Springer-Verlag New York, Inc. 2004. 
[5]. J.Likeš, J. Laga, “Základní Statiscke Tabulky", Nakl. tech. literatury, Praha 1978. 
 ABSTRACT 
 A METHOD OF CALCULATING THE CORRELATION BETWEEN THE 
 MACHINE CLOCK AND THE ADDITION OF TWO INTEGER WHEN 
 IMPLEMENTED ON HARDWARE 
 In the implementation of public-key cryptography systems, numerical 
 calculations on the large integer calculation is always important and hardest. 
 To assess the level of resource consumption as well as the speed of execution of 
 this operation, in this paper we propose a method of calculating the correlation 
 between the machine clock and the addition of two integers to real on 
 hardware. 
Keywords: Addition, machine clock, Elliptic Curve Cryptography. 
 Nhận bài ngày 15 tháng 6 năm 2014 
 Hoàn thiện ngày 10 tháng 9 năm 2014 
 Chấp nhận đăng ngày 25 tháng 9 năm 2014 
 Địa chỉ: * Ban Cơ yếu Chính phủ; 
 ** Cục Cơ yếu – BTTM; DĐ 0983074784. 
T¹p chÝ Nghiªn cøu KH&CN qu©n sù, Sè 33, 10 - 2014 81