Một phương pháp thiết kế ngữ nghĩa tính toán của các từ ngôn ngữ giải bài toán phân lớp dựa trên luật mờ

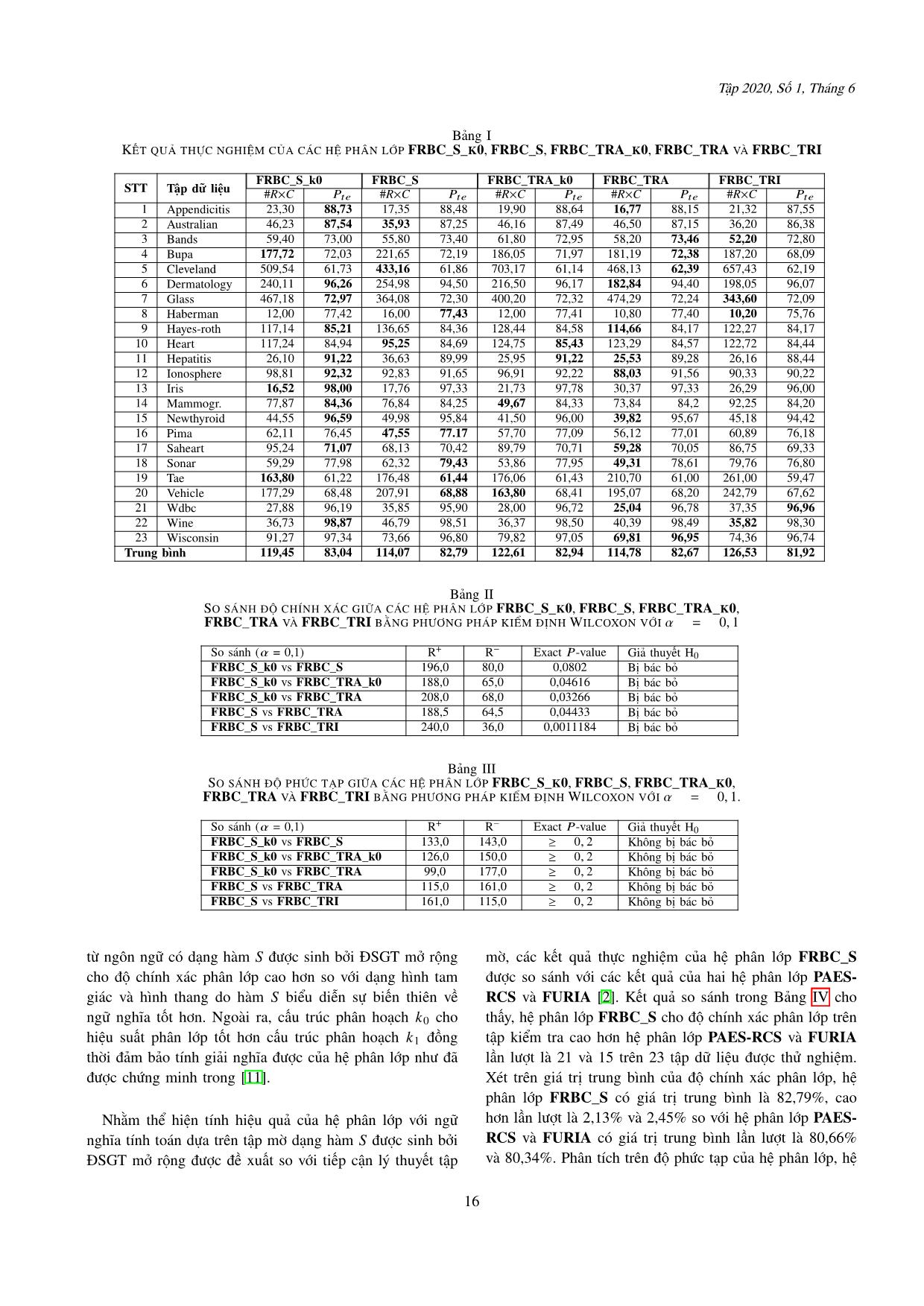
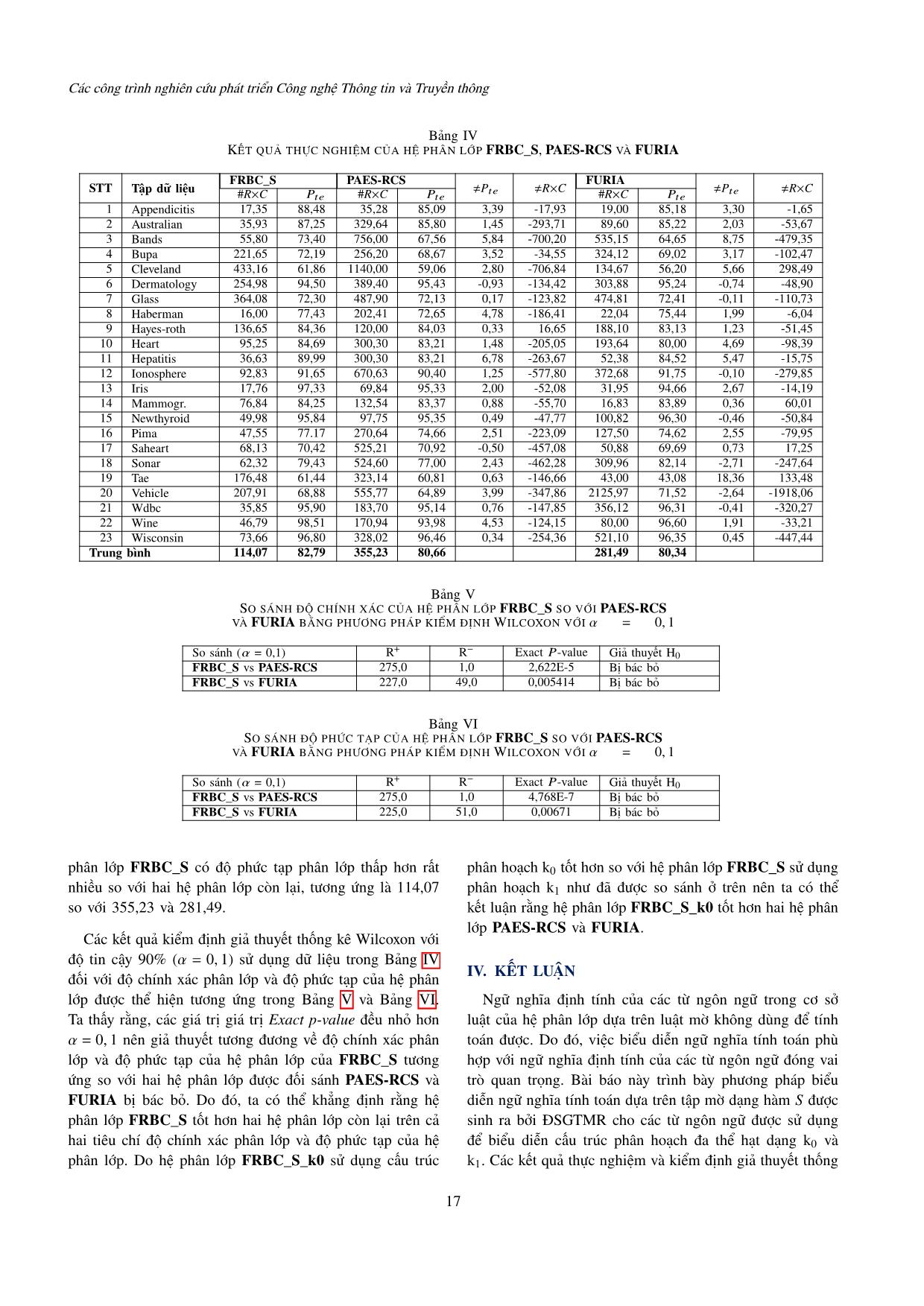
thế cách biểu diễn phân hoạch mờ thì các hệ phân lớp dựa trên
 hệ là 1500; số luật khởi tạo là |S0| = 300 × số lớp; độ dài luật mờ với ngữ nghĩa tính toán dựa trên tập mờ của các
 15
 Tập 2020, Số 1, Tháng 6
 Bảng I
 KẾT QUẢ THỰC NGHIỆM CỦA CÁC HỆ PHÂN LỚP FRBC_S_K0, FRBC_S, FRBC_TRA_K0, FRBC_TRA VÀ FRBC_TRI
 FRBC_S_k0 FRBC_S FRBC_TRA_k0 FRBC_TRA FRBC_TRI
 STT Tập dữ liệu
 #R×C 푃푡푒 #R×C 푃푡푒 #R×C 푃푡푒 #R×C 푃푡푒 #R×C 푃푡푒
 1 Appendicitis 23,30 88,73 17,35 88,48 19,90 88,64 16,77 88,15 21,32 87,55
 2 Australian 46,23 87,54 35,93 87,25 46,16 87,49 46,50 87,15 36,20 86,38
 3 Bands 59,40 73,00 55,80 73,40 61,80 72,95 58,20 73,46 52,20 72,80
 4 Bupa 177,72 72,03 221,65 72,19 186,05 71,97 181,19 72,38 187,20 68,09
 5 Cleveland 509,54 61,73 433,16 61,86 703,17 61,14 468,13 62,39 657,43 62,19
 6 Dermatology 240,11 96,26 254,98 94,50 216,50 96,17 182,84 94,40 198,05 96,07
 7 Glass 467,18 72,97 364,08 72,30 400,20 72,32 474,29 72,24 343,60 72,09
 8 Haberman 12,00 77,42 16,00 77,43 12,00 77,41 10,80 77,40 10,20 75,76
 9 Hayes-roth 117,14 85,21 136,65 84,36 128,44 84,58 114,66 84,17 122,27 84,17
 10 Heart 117,24 84,94 95,25 84,69 124,75 85,43 123,29 84,57 122,72 84,44
 11 Hepatitis 26,10 91,22 36,63 89,99 25,95 91,22 25,53 89,28 26,16 88,44
 12 Ionosphere 98,81 92,32 92,83 91,65 96,91 92,22 88,03 91,56 90,33 90,22
 13 Iris 16,52 98,00 17,76 97,33 21,73 97,78 30,37 97,33 26,29 96,00
 14 Mammogr. 77,87 84,36 76,84 84,25 49,67 84,33 73,84 84,2 92,25 84,20
 15 Newthyroid 44,55 96,59 49,98 95,84 41,50 96,00 39,82 95,67 45,18 94,42
 16 Pima 62,11 76,45 47,55 77.17 57,70 77,09 56,12 77,01 60,89 76,18
 17 Saheart 95,24 71,07 68,13 70,42 89,79 70,71 59,28 70,05 86,75 69,33
 18 Sonar 59,29 77,98 62,32 79,43 53,86 77,95 49,31 78,61 79,76 76,80
 19 Tae 163,80 61,22 176,48 61,44 176,06 61,43 210,70 61,00 261,00 59,47
 20 Vehicle 177,29 68,48 207,91 68,88 163,80 68,41 195,07 68,20 242,79 67,62
 21 Wdbc 27,88 96,19 35,85 95,90 28,00 96,72 25,04 96,78 37,35 96,96
 22 Wine 36,73 98,87 46,79 98,51 36,37 98,50 40,39 98,49 35,82 98,30
 23 Wisconsin 91,27 97,34 73,66 96,80 79,82 97,05 69,81 96,95 74,36 96,74
 Trung bình 119,45 83,04 114,07 82,79 122,61 82,94 114,78 82,67 126,53 81,92
 Bảng II
 SO SÁNH ĐỘ CHÍNH XÁC GIỮA CÁC HỆ PHÂN LỚP FRBC_S_K0, FRBC_S, FRBC_TRA_K0,
 FRBC_TRA VÀ FRBC_TRI BẰNG PHƯƠNG PHÁP KIỂM ĐỊNH WILCOXON VỚI 훼 = 0, 1
 + −
 So sánh (훼 = 0,1) R R Exact 푃-value Giả thuyết H0
 FRBC_S_k0 vs FRBC_S 196,0 80,0 0,0802 Bị bác bỏ
 FRBC_S_k0 vs FRBC_TRA_k0 188,0 65,0 0,04616 Bị bác bỏ
 FRBC_S_k0 vs FRBC_TRA 208,0 68,0 0,03266 Bị bác bỏ
 FRBC_S vs FRBC_TRA 188,5 64,5 0,04433 Bị bác bỏ
 FRBC_S vs FRBC_TRI 240,0 36,0 0,0011184 Bị bác bỏ
 Bảng III
 SO SÁNH ĐỘ PHỨC TẠP GIỮA CÁC HỆ PHÂN LỚP FRBC_S_K0, FRBC_S, FRBC_TRA_K0,
 FRBC_TRA VÀ FRBC_TRI BẰNG PHƯƠNG PHÁP KIỂM ĐỊNH WILCOXON VỚI 훼 = 0, 1.
 + −
 So sánh (훼 = 0,1) R R Exact 푃-value Giả thuyết H0
 FRBC_S_k0 vs FRBC_S 133,0 143,0 ≥ 0, 2 Không bị bác bỏ
 FRBC_S_k0 vs FRBC_TRA_k0 126,0 150,0 ≥ 0, 2 Không bị bác bỏ
 FRBC_S_k0 vs FRBC_TRA 99,0 177,0 ≥ 0, 2 Không bị bác bỏ
 FRBC_S vs FRBC_TRA 115,0 161,0 ≥ 0, 2 Không bị bác bỏ
 FRBC_S vs FRBC_TRI 161,0 115,0 ≥ 0, 2 Không bị bác bỏ
từ ngôn ngữ có dạng hàm 푆 được sinh bởi ĐSGT mở rộng mờ, các kết quả thực nghiệm của hệ phân lớp FRBC_S
cho độ chính xác phân lớp cao hơn so với dạng hình tam được so sánh với các kết quả của hai hệ phân lớp PAES-
giác và hình thang do hàm 푆 biểu diễn sự biến thiên về RCS và FURIA [2]. Kết quả so sánh trong Bảng IV cho
ngữ nghĩa tốt hơn. Ngoài ra, cấu trúc phân hoạch 0 cho thấy, hệ phân lớp FRBC_S cho độ chính xác phân lớp trên
hiệu suất phân lớp tốt hơn cấu trúc phân hoạch 1 đồng tập kiểm tra cao hơn hệ phân lớp PAES-RCS và FURIA
thời đảm bảo tính giải nghĩa được của hệ phân lớp như đã lần lượt là 21 và 15 trên 23 tập dữ liệu được thử nghiệm.
được chứng minh trong [11]. Xét trên giá trị trung bình của độ chính xác phân lớp, hệ
 phân lớp FRBC_S có giá trị trung bình là 82,79%, cao
 Nhằm thể hiện tính hiệu quả của hệ phân lớp với ngữ hơn lần lượt là 2,13% và 2,45% so với hệ phân lớp PAES-
nghĩa tính toán dựa trên tập mờ dạng hàm 푆 được sinh bởi RCS và FURIA có giá trị trung bình lần lượt là 80,66%
ĐSGT mở rộng được đề xuất so với tiếp cận lý thuyết tập và 80,34%. Phân tích trên độ phức tạp của hệ phân lớp, hệ
 16
Các công trình nghiên cứu phát triển Công nghệ Thông tin và Truyền thông
 Bảng IV
 KẾT QUẢ THỰC NGHIỆM CỦA HỆ PHÂN LỚP FRBC_S, PAES-RCS VÀ FURIA
 FRBC_S PAES-RCS FURIA
 STT Tập dữ liệu ≠P푡푒 ≠R×C ≠P푡푒 ≠R×C
 #R×C 푃푡푒 #R×C 푃푡푒 #R×C 푃푡푒
 1 Appendicitis 17,35 88,48 35,28 85,09 3,39 -17,93 19,00 85,18 3,30 -1,65
 2 Australian 35,93 87,25 329,64 85,80 1,45 -293,71 89,60 85,22 2,03 -53,67
 3 Bands 55,80 73,40 756,00 67,56 5,84 -700,20 535,15 64,65 8,75 -479,35
 4 Bupa 221,65 72,19 256,20 68,67 3,52 -34,55 324,12 69,02 3,17 -102,47
 5 Cleveland 433,16 61,86 1140,00 59,06 2,80 -706,84 134,67 56,20 5,66 298,49
 6 Dermatology 254,98 94,50 389,40 95,43 -0,93 -134,42 303,88 95,24 -0,74 -48,90
 7 Glass 364,08 72,30 487,90 72,13 0,17 -123,82 474,81 72,41 -0,11 -110,73
 8 Haberman 16,00 77,43 202,41 72,65 4,78 -186,41 22,04 75,44 1,99 -6,04
 9 Hayes-roth 136,65 84,36 120,00 84,03 0,33 16,65 188,10 83,13 1,23 -51,45
 10 Heart 95,25 84,69 300,30 83,21 1,48 -205,05 193,64 80,00 4,69 -98,39
 11 Hepatitis 36,63 89,99 300,30 83,21 6,78 -263,67 52,38 84,52 5,47 -15,75
 12 Ionosphere 92,83 91,65 670,63 90,40 1,25 -577,80 372,68 91,75 -0,10 -279,85
 13 Iris 17,76 97,33 69,84 95,33 2,00 -52,08 31,95 94,66 2,67 -14,19
 14 Mammogr. 76,84 84,25 132,54 83,37 0,88 -55,70 16,83 83,89 0,36 60,01
 15 Newthyroid 49,98 95,84 97,75 95,35 0,49 -47,77 100,82 96,30 -0,46 -50,84
 16 Pima 47,55 77.17 270,64 74,66 2,51 -223,09 127,50 74,62 2,55 -79,95
 17 Saheart 68,13 70,42 525,21 70,92 -0,50 -457,08 50,88 69,69 0,73 17,25
 18 Sonar 62,32 79,43 524,60 77,00 2,43 -462,28 309,96 82,14 -2,71 -247,64
 19 Tae 176,48 61,44 323,14 60,81 0,63 -146,66 43,00 43,08 18,36 133,48
 20 Vehicle 207,91 68,88 555,77 64,89 3,99 -347,86 2125,97 71,52 -2,64 -1918,06
 21 Wdbc 35,85 95,90 183,70 95,14 0,76 -147,85 356,12 96,31 -0,41 -320,27
 22 Wine 46,79 98,51 170,94 93,98 4,53 -124,15 80,00 96,60 1,91 -33,21
 23 Wisconsin 73,66 96,80 328,02 96,46 0,34 -254,36 521,10 96,35 0,45 -447,44
 Trung bình 114,07 82,79 355,23 80,66 281,49 80,34
 Bảng V
 SO SÁNH ĐỘ CHÍNH XÁC CỦA HỆ PHÂN LỚP FRBC_S SO VỚI PAES-RCS
 VÀ FURIA BẰNG PHƯƠNG PHÁP KIỂM ĐỊNH WILCOXON VỚI 훼 = 0, 1
 + −
 So sánh (훼 = 0,1) R R Exact 푃-value Giả thuyết H0
 FRBC_S vs PAES-RCS 275,0 1,0 2,622E-5 Bị bác bỏ
 FRBC_S vs FURIA 227,0 49,0 0,005414 Bị bác bỏ
 Bảng VI
 SO SÁNH ĐỘ PHỨC TẠP CỦA HỆ PHÂN LỚP FRBC_S SO VỚI PAES-RCS
 VÀ FURIA BẰNG PHƯƠNG PHÁP KIỂM ĐỊNH WILCOXON VỚI 훼 = 0, 1
 + −
 So sánh (훼 = 0,1) R R Exact 푃-value Giả thuyết H0
 FRBC_S vs PAES-RCS 275,0 1,0 4,768E-7 Bị bác bỏ
 FRBC_S vs FURIA 225,0 51,0 0,00671 Bị bác bỏ
phân lớp FRBC_S có độ phức tạp phân lớp thấp hơn rất phân hoạch k0 tốt hơn so với hệ phân lớp FRBC_S sử dụng
nhiều so với hai hệ phân lớp còn lại, tương ứng là 114,07 phân hoạch k1 như đã được so sánh ở trên nên ta có thể
so với 355,23 và 281,49. kết luận rằng hệ phân lớp FRBC_S_k0 tốt hơn hai hệ phân
 lớp PAES-RCS và FURIA.
 Các kết quả kiểm định giả thuyết thống kê Wilcoxon với
độ tin cậy 90% (훼 = 0, 1) sử dụng dữ liệu trong Bảng IV
 IV. KẾT LUẬN
đối với độ chính xác phân lớp và độ phức tạp của hệ phân
lớp được thể hiện tương ứng trong Bảng V và Bảng VI. Ngữ nghĩa định tính của các từ ngôn ngữ trong cơ sở
Ta thấy rằng, các giá trị giá trị Exact p-value đều nhỏ hơn luật của hệ phân lớp dựa trên luật mờ không dùng để tính
훼 = 0, 1 nên giả thuyết tương đương về độ chính xác phân toán được. Do đó, việc biểu diễn ngữ nghĩa tính toán phù
lớp và độ phức tạp của hệ phân lớp của FRBC_S tương hợp với ngữ nghĩa định tính của các từ ngôn ngữ đóng vai
ứng so với hai hệ phân lớp được đối sánh PAES-RCS và trò quan trọng. Bài báo này trình bày phương pháp biểu
FURIA bị bác bỏ. Do đó, ta có thể khẳng định rằng hệ diễn ngữ nghĩa tính toán dựa trên tập mờ dạng hàm 푆 được
phân lớp FRBC_S tốt hơn hai hệ phân lớp còn lại trên cả sinh ra bởi ĐSGTMR cho các từ ngôn ngữ được sử dụng
hai tiêu chí độ chính xác phân lớp và độ phức tạp của hệ để biểu diễn cấu trúc phân hoạch đa thể hạt dạng k0 và
phân lớp. Do hệ phân lớp FRBC_S_k0 sử dụng cấu trúc k1. Các kết quả thực nghiệm và kiểm định giả thuyết thống
 17
 Tập 2020, Số 1, Tháng 6
kê Wilcoxon cho thấy tính hiệu quả của các phương pháp [14] N. H. Huy, N. C. Ho, N. V. Quyen, “Multichannel image
được đề xuất khi áp dụng cho hệ phân lớp dựa trên luật contrast enhancement based on linguistic rule-based inten-
 sificators,” Applied Soft Computing Journal, vol. 76, pp.
mờ. 744–762, 2019.
 [15] D. T. Long, “A genetic algorithm based method for
 timetabling problems using linguistics of hedge algebra in
LỜI CẢM ƠN constraints,” Journal of Computer Science and Cybernet-
 ics, vol. 32, no. 4, pp. 285–301, 2016.
 [16] J. Demsar, “Statistical Comparisons of Classifiers over
 Nghiên cứu này được tài trợ bởi Trường Đại học Giao Multiple Data Sets,” Journal of Machine Learning Re-
thông vận tải trong đề tài mã số T2020-CN-002. search, vol. 7, pp. 1–30, 2006.
 [17] P. D. Phong, N. C. Ho, N. T. Thuy, “Multi-objective Par-
 ticle Swarm Optimization Algorithm and its Application
 to the Fuzzy Rule Based Classifier Design Problem with
TÀI LIỆU THAM KHẢO the Order Based Semantics of Linguistic Terms,” In Pro-
 [1] R. Alcalá, Y. Nojima, F. Herrera, H. Ishibuchi, “Multi- ceedings of The 10th IEEE RIVF International Conference
 objective genetic fuzzy rule selection of single granularity- on Computing and Communication Technologies (RIVF-
 based fuzzy classification rules and its interaction with the 2013), Hanoi, Vietnam, pp. 12–17, 2013.
 lateral tuning of membership functions,” Soft Computing, [18] F. Rudzinski, “A multi-objective genetic optimization of
 vol. 15, no. 12, pp. 2303–2318, 2011. interpretability-oriented fuzzy rule-based classifiers,” Ap-
 [2] M. Antonelli, P. Ducange, F. Marcelloni, “A fast and plied Soft Computing, vol. 38, pp. 118–133, 2016.
 efficient multi-objective evolutionary learning scheme for [19] M. Elkanoa, M. Galara, J. Sanza, H. Bustince, “CHI-
 fuzzy rule-based classifiers,” Information Sciences, vol. BD: A fuzzy rule-based classification system for Big Data
 283, pp. 36–54, 2014. classification problems,” Fuzzy Sets and Systems, vol. 348,
 [3] H. Ishibuchi, T. Yamamoto, “Fuzzy Rule Selection by pp. 75–101, 2018.
 Multi-Objective Genetic Local Search Algorithms and [20] M. Pota, M. Esposito, G. D. Pietro, “Designing rule-based
 Rule Evaluation Measures in Data Mining,” Fuzzy Sets and fuzzy systems for classification in medicine,” Knowledge-
 Systems, vol. 141, no. 1, pp. 59-88, 2014. Based Systems, vol. 124, pp. 105–132, 2017.
 [4] H. Ishibuchi, T. Yamamoto, “Rule weight specification in [21] M. Soui, I. Gasmi, S. Smiti, K. Ghédira, "Rule-based credit
 fuzzy rule-based classification systems,” IEEE Transac- risk assessment model using multi-objective evolutionary
 tions on Fuzzy Systems, vol. 13, no. 4, pp. 428–435, 2005. algorithms," Expert Systems With Applications, vol. 126,
 [5] M. I. Rey, M. Galende, M. J. Fuente, G. I. Sainz- pp. 144–157, 2019.
 Palmero, “Multi-objective based Fuzzy Rule Based Sys- [22] Y. Zhang, X. Qian, J. Wang, M. Gendeel1, "Fuzzy rule-
 tems (FRBSs) for trade-off improvement in accuracy based classification system using multi-population quan-
 and interpretability: A rule relevance point of view,” tum evolutionary algorithm with contradictory rule recon-
 Knowledge-Based Systems, vol. 127, pp. 67–84, 2017. struction," Applied Intelligence, vol. 49, pp. 4007–4021,
 [6] N. C. Ho, W. Wechler, “Hedge algebras: an algebraic 2019.
 approach to structures of sets of linguistic domains of
 linguistic truth variables,” Fuzzy Sets and Systems, vol. 35,
 no. 3, pp. 281-293, 1990.
 [7] N. C. Ho, W. Wechler, “Extended hedge algebras and their
 application to fuzzy logic,” Fuzzy Sets and Systems, vol.
 52, pp. 259–281, 1992.
 [8] N. C. Ho, N. V. Long, “Fuzziness measure on complete
 hedges algebras and quantifying semantics of terms in
 linear hedge algebras,” Fuzzy Sets and Systems, vol. 158,
 pp. 452-471, 2007.
 [9] N. C. Ho, W. Pedrycz, D. T. Long, T. T. Son, “A genetic
 design of linguistic terms for fuzzy rule based classifiers,”
 International Journal of Approximate Reasoning, vol 54,
 no. 1, pp. 1-21, 2013.
 [10] N. C. Ho, T. T. Son, P. D. Phong, “Modeling of a semantics
 core of linguistic terms based on an extension of hedge
 algebra semantics and its application,” Knowledge-Based
 Systems, vol. 67, pp. 244–262, 2014.
 [11] N. C. Ho, H. V. Thong, N. V. Long, “A discussion
 on interpretability of linguistic rule based systems and
 its application to solve regression problems,” Knowledge-
 Based Systems, vol. 88, pp. 107–133, 2015.
 [12] T. T. Son, N. T. Anh, “Partition fuzzy domain with multi-
 granularity representation of data based on hedge algebra
 approach,” Journal of Computer Science and Cybernetics,
 vol. 34, no. 1, pp. 63–75, 2018.
 [13] B. H. Le, L. T. Anh, B. V. Binh, “Explicit formula of
 hedge-algebras-based fuzzy controller and applications in
 structural vibration control,” Applied Soft Computing, vol.
 60, pp. 150–166, 2017.
 18
 Các công trình nghiên cứu phát triển Công nghệ Thông tin và Truyền thông
SƠ LƯỢC VỀ CÁC TÁC GIẢ Nguyễn Đức Thảo
 Nhận bằng Kỹ sư, Thạc sĩ và
 Nguyễn Đức Dư Tiến sỹ Công nghệ thông tin lần
 Nhận bằng Cử nhân Toán tin lượt tại Trường Đại học Tổng
 ứng dụng, Thạc sĩ Toán ứng hợp Nga năm 1996, 2001. Hiện
 dụng tại Trường Đại học khoa là cán bộ nghiên cứu tại Viện
 học tự nhiên, Đại học Quốc gia Khoa học và Công nghệ quân
 Hà Nội lần lượt các năm 2001, sự/ Bộ Quốc phòng. Lĩnh vực
 2005. Hiện là giảng viên Khoa nghiên cứu: khai phá dữ liệu, lô
 Công nghệ thông tin, Trường gic mờ, hệ mờ, tính toán mềm,
 Đại học Giao thông vận tải. tính toán với từ, học máy, trí tuệ
 Lĩnh vực nghiên cứu: khai phá nhân tạo, hệ thống thông tin, hệ
 dữ liệu, lô gic mờ, hệ mờ, tính chuyên gia.
 toán mềm, tính toán với từ, học
 máy.
Phạm Đình Phong
 Nhận bằng Thạc sĩ Công nghệ
 thông tin và Tiến sĩ Khoa học
 máy tính tại Trường Đại học
 Công nghệ, Đại học Quốc
 gia Hà Nội lần lượt các năm
 2011, 2018. Hiện là giảng
 viên Khoa Công nghệ thông
 tin, Trường Đại học Giao
 thông vận tải. Lĩnh Vực nghiên
 cứu: khai phá dữ liệu, các
 hệ mờ, tính toán mềm, học
 máy.
Phạm Đình Vũ
 Nhận bằng kỹ sư Công nghệ
 thông tin tại Trường Đại học
 Bách khoa Hà Nội năm 2003,
 Thạc sỹ Hệ thống thông tin Học
 viện Công nghệ Bưu chính Viễn
 thông năm 2015. Hiện đang
 công tác tại Cục Công nghệ
 thông tin và Thống kê hải quan,
 Tổng cục Hải quan. Lĩnh vực
 nghiên cứu: khai phá dữ liệu,
 các hệ mờ, tính toán mềm, học
 máy.
 19