Mô hình MOORA dựa vào entropy mờ mới ứng dụng cho hệ thống thông tin tuyển dụng

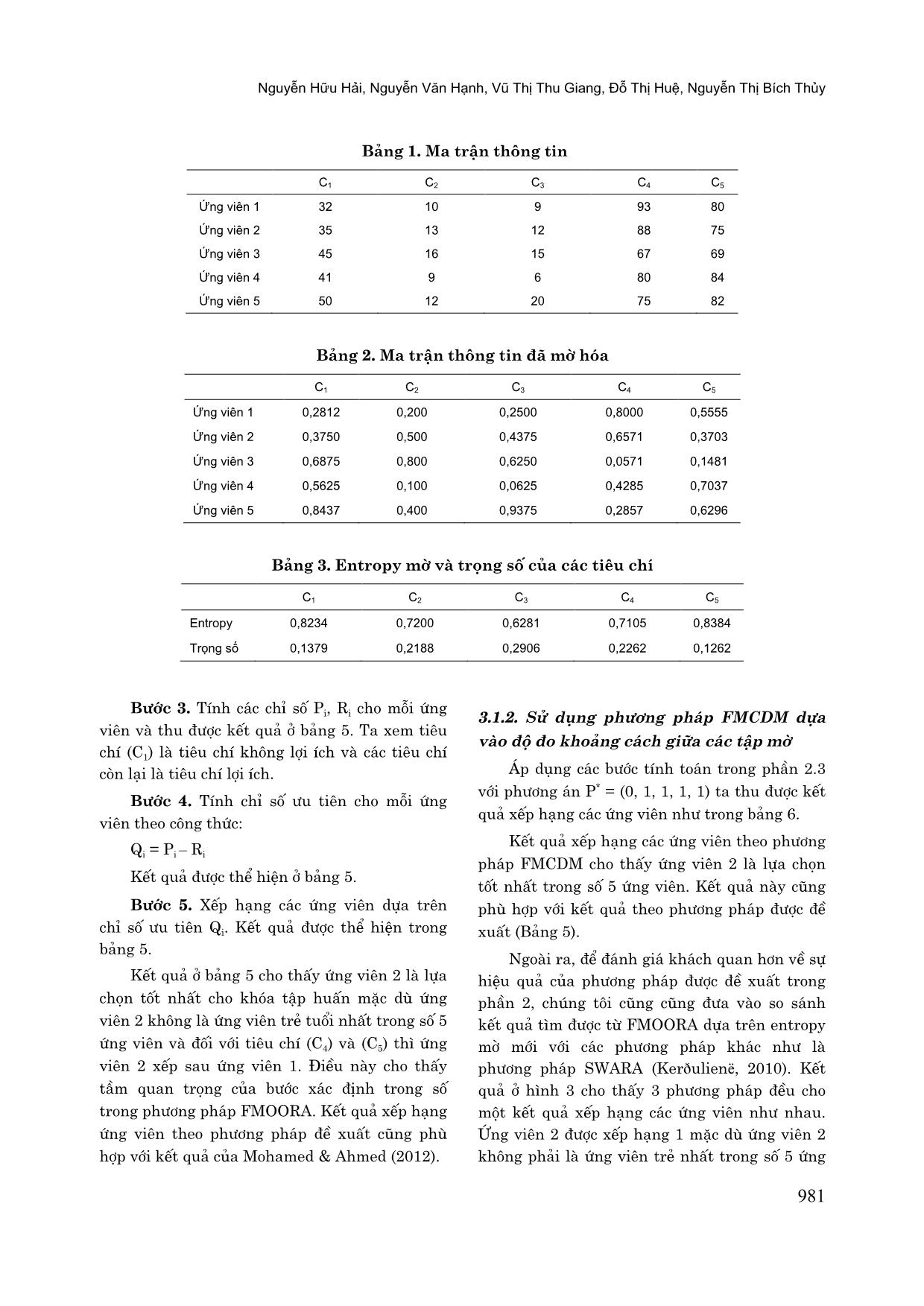
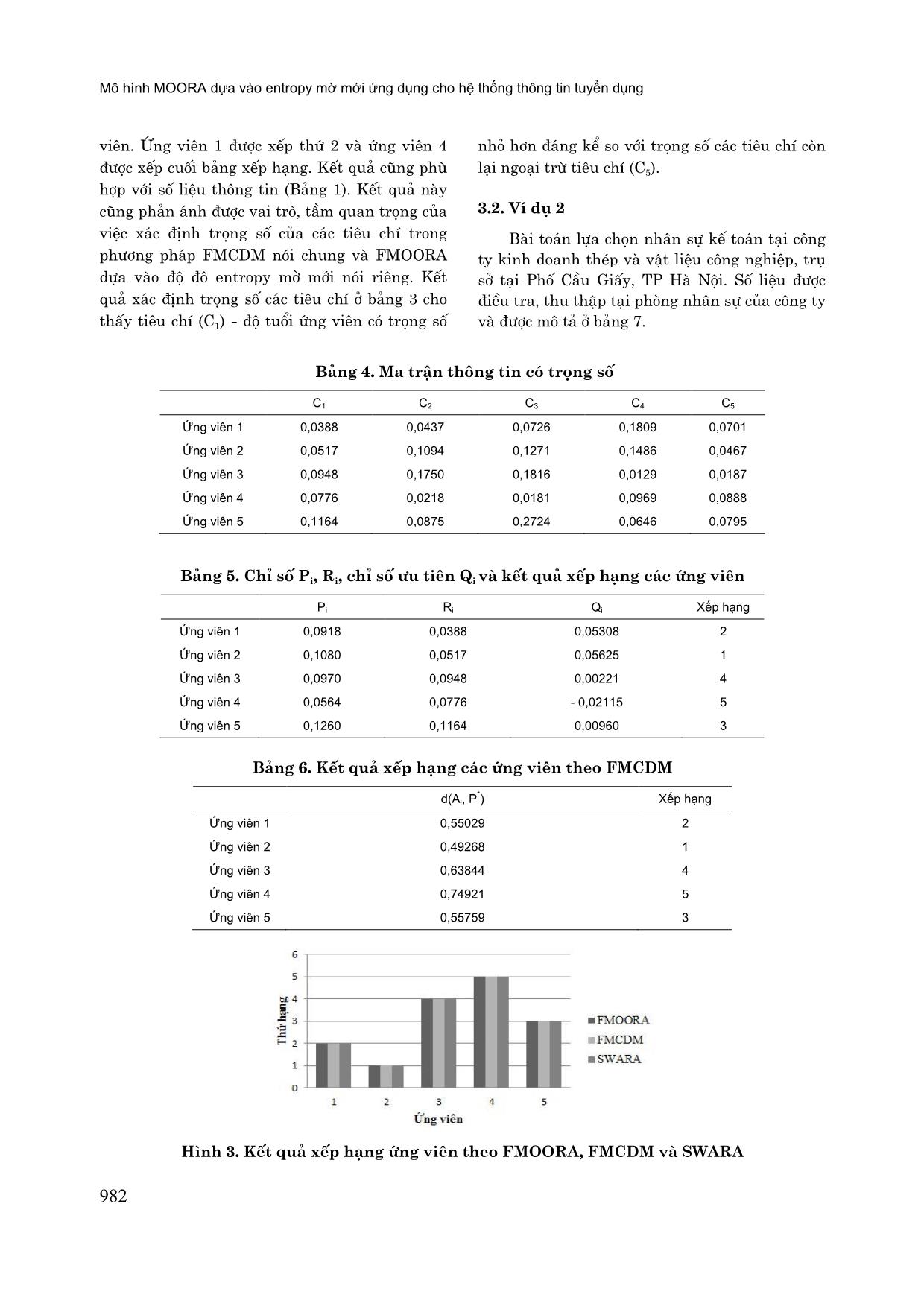
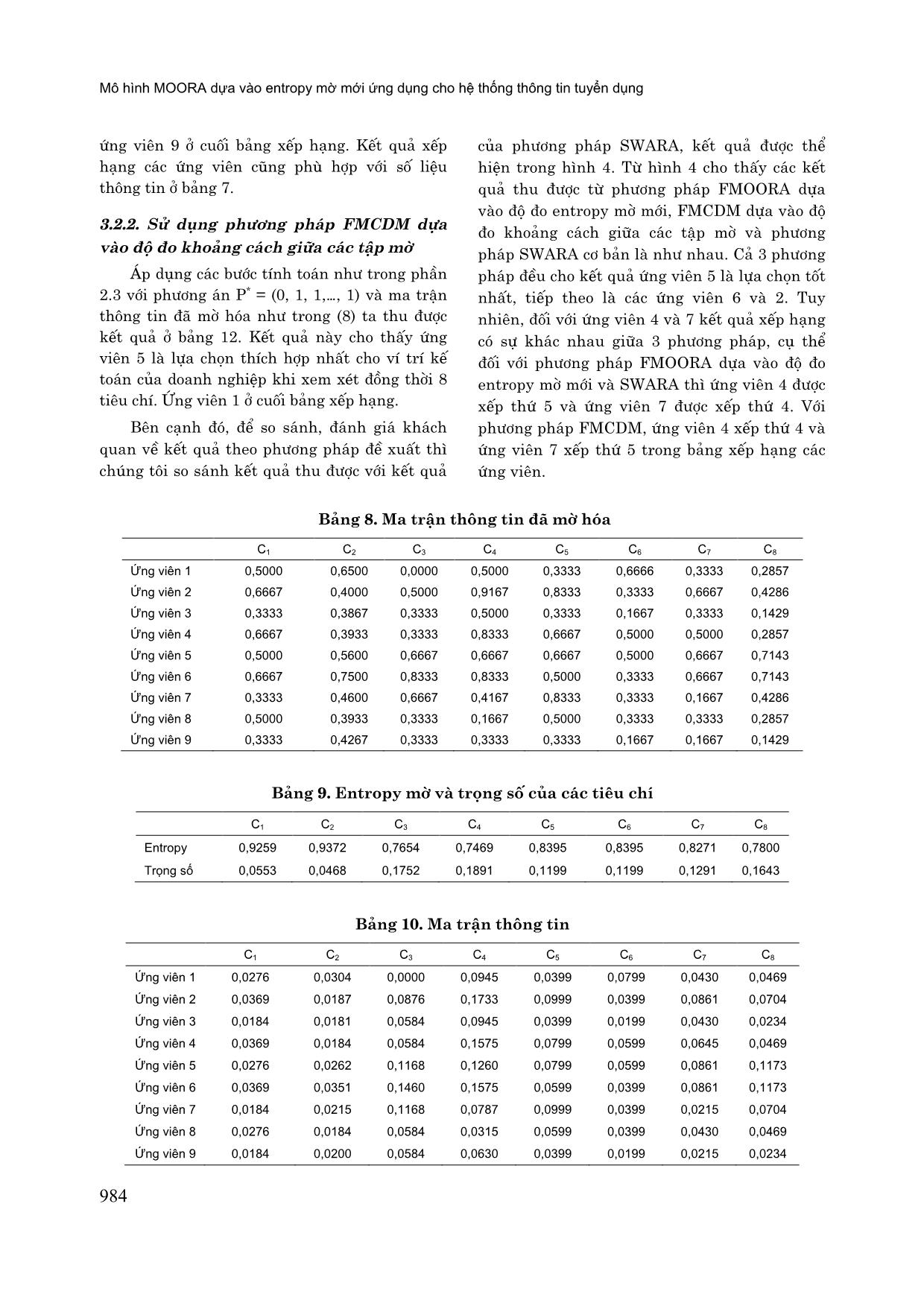
 các tập mờ 
Áp dụng các bước tính toán trong phần 2.3 
với phương án P* = (0, 1, 1, 1, 1) ta thu được kết 
quả xếp hạng các ứng viên như trong bảng 6. 
Kết quả xếp hạng các ứng viên theo phương 
pháp FMCDM cho thấy ứng viên 2 là lựa chọn 
tốt nhất trong số 5 ứng viên. Kết quả này cũng 
phù hợp với kết quả theo phương pháp được đề 
xuất (Bảng 5). 
Ngoài ra, để đánh giá khách quan hơn về sự 
hiệu quả của phương pháp được đề xuất trong 
phần 2, chúng tôi cũng cũng đưa vào so sánh 
kết quả tìm được từ FMOORA dựa trên entropy 
mờ mới với các phương pháp khác như là 
phương pháp SWARA (Kerðulienë, 2010). Kết 
quả ở hình 3 cho thấy 3 phương pháp đều cho 
một kết quả xếp hạng các ứng viên như nhau. 
Ứng viên 2 được xếp hạng 1 mặc dù ứng viên 2 
không phải là ứng viên trẻ nhất trong số 5 ứng 
Mô hình MOORA dựa vào entropy mờ mới ứng dụng cho hệ thống thông tin tuyển dụng 
982 
viên. Ứng viên 1 được xếp thứ 2 và ứng viên 4 
được xếp cuối bảng xếp hạng. Kết quả cũng phù 
hợp với số liệu thông tin (Bảng 1). Kết quả này 
cũng phản ánh được vai trò, tầm quan trọng của 
việc xác định trọng số của các tiêu chí trong 
phương pháp FMCDM nói chung và FMOORA 
dựa vào độ đô entropy mờ mới nói riêng. Kết 
quả xác định trọng số các tiêu chí ở bảng 3 cho 
thấy tiêu chí (C1) 
- độ tuổi ứng viên có trọng số 
nhỏ hơn đáng kể so với trọng số các tiêu chí còn 
lại ngoại trừ tiêu chí (C5). 
3.2. Ví dụ 2 
Bài toán lựa chọn nhân sự kế toán tại công 
ty kinh doanh thép và vật liệu công nghiệp, trụ 
sở tại Phố Cầu Giấy, TP Hà Nội. Số liệu được 
điều tra, thu thập tại phòng nhân sự của công ty 
và được mô tả ở bảng 7. 
 Bảng 4. Ma trận thông tin có trọng số 
 C1 C2 C3 C4 C5 
Ứng viên 1 0,0388 0,0437 0,0726 0,1809 0,0701 
Ứng viên 2 0,0517 0,1094 0,1271 0,1486 0,0467 
Ứng viên 3 0,0948 0,1750 0,1816 0,0129 0,0187 
Ứng viên 4 0,0776 0,0218 0,0181 0,0969 0,0888 
Ứng viên 5 0,1164 0,0875 0,2724 0,0646 0,0795 
Bảng 5. Chỉ số Pi, Ri, chỉ số ưu tiên Qi và kết quả xếp hạng các ứng viên 
 Pi Ri Qi Xếp hạng 
Ứng viên 1 0,0918 0,0388 0,05308 2 
Ứng viên 2 0,1080 0,0517 0,05625 1 
Ứng viên 3 0,0970 0,0948 0,00221 4 
Ứng viên 4 0,0564 0,0776 - 0,02115 5 
Ứng viên 5 0,1260 0,1164 0,00960 3 
Bảng 6. Kết quả xếp hạng các ứng viên theo FMCDM 
 d(Ai, P
*
) Xếp hạng 
Ứng viên 1 0,55029 2 
Ứng viên 2 0,49268 1 
Ứng viên 3 0,63844 4 
Ứng viên 4 0,74921 5 
Ứng viên 5 0,55759 3 
Hình 3. Kết quả xếp hạng ứng viên theo FMOORA, FMCDM và SWARA 
Nguyễn Hữu Hải, Nguyễn Văn Hạnh, Vũ Thị Thu Giang, Đỗ Thị Huệ, Nguyễn Thị Bích Thủy 
983 
Bảng 7. Ma trận thông tin 
 C1 C2 C3 C4 C5 C6 C7 C8 
Ứng viên 1 28 3,0 7,85 5,0 80 70 65 1,0 
Ứng viên 2 29 5,5 7,10 6,5 70 80 70 1,5 
Ứng viên 3 27 3,0 7,06 5,0 65 70 60 1,0 
Ứng viên 4 29 5,0 7,08 6,0 75 75 65 1,0 
Ứng viên 5 28 4,0 7,58 6,0 75 80 80 2,0 
Ứng viên 6 29 5,0 8,15 5,5 70 80 80 2,5 
Ứng viên 7 27 2,5 7,28 6,5 70 65 70 2,0 
Ứng viên 8 28 1,0 7,08 5,5 70 70 65 1,0 
Ứng viên 9 27 2,0 7,18 5,0 65 65 60 1,0 
Trong ví dụ này chúng tôi sử dụng 8 tiêu 
chí để đánh giá ứng viên bao gồm: độ tuổi ứng 
viên (C1), kinh nghiệm làm việc (C2), trình độ 
học vấn (C3), năng lực ngoại ngữ (C4), mức độ 
thành thạo MS office (C5), kỹ năng sử dụng 
phần mềm kế toán (C6), kỹ năng làm việc nhóm 
(C7) và điểm cộng (C8). Chúng tôi sử dụng tiêu 
chí điểm cộng để cộng điểm cho ứng viên tốt 
nghiệp từ các trường đại học có uy tín trong lĩnh 
vực kinh tế - kế toán hay là các ứng viên đã qua 
đào tạo trình độ thạc sỹ chuyên ngành kế toán. 
Điều này nhằm phản ánh sát thực tế hơn trong 
lĩnh vực tuyển dụng nhân sự tại các công ty và 
doanh nghiệp. 
3.2.1. Sử dụng mô hình FMOORA dựa vào 
entropy mờ mới 
Tương tự như ví dụ 1, các bước của phương 
pháp FMOORA dựa vào entropy mờ mới được 
thực hiện như sau: 
Bước 1. Tính trọng số của các tiêu chí Cj, 
j = 1, 2,, 5 theo công thức (4) và (5). Kết quả 
thu được ở bảng 9. 
 Trước hết, ta cần mờ hóa ma trận thông tin 
dựa vào số mờ ở công thức (3), cụ thể với c = 25, 
d = 32 cho tiêu chí (C1); c = 0, d = 6 cho tiêu chí 
(C2); c = 6, d = 9 cho tiêu chí (C3); c = 4, d = 7 cho 
tiêu chí (C4); c = 60, d = 90 cho tiêu chí (C5) và 
(C6); c = 55, d = 90 cho tiêu chí (C7); c = 0, d = 3 
cho tiêu chí (C8), kết quả thu được ở bảng 8. 
Tiếp theo chúng ta cần tính độ đo entropy 
mờ của các tiêu chí theo công thức (4), tính 
trọng số của các tiêu chí theo công thức (5) thu 
được kết quả như trong bảng 9. Kết quả này cho 
thấy tiêu chí (C4) có trọng số lớn nhất, tiếp theo 
là tiêu chí (C3) 
và tiêu chí (C2) 
có trọng số bé 
nhất. Tiêu chí (C2) 
và (C1) có trọng số bé hơn 
đáng kể so với trọng số các tiêu chí còn lại. Số 
liệu ở bảng 9 cho thấy ngoài vai trò quan trọng 
của tiêu chí (C3) và (C4)thì các tiêu chí (C5) - (C8) 
cũng đóng vai trò đáng kể trong việc xếp hạng 
các ứng viên. 
Bước 2. Xác định ma trận thông tin có 
trọng số theo công thức (5). Kết quả thu được ở 
bảng 10. 
Bước 3. Tính các chỉ số Pi, Ri cho mỗi ứng 
viên và thu được kết quả ở bảng 11. 
Bước 4. Tính chỉ số ưu tiên cho mỗi ứng 
viên theo công thức: 
Qi = Pi - Ri 
Kết quả được thể hiện trong bảng 11. Trong 
8 tiêu chí được xem xét thì tiêu chí (C1) được 
xem là tiêu chí không lợi ích và các tiêu chí còn 
lại là tiêu chí lợi ích. 
Bước 5. Xếp hạng các ứng viên dựa trên 
chỉ số ưu tiên Qi. Kết quả được thể hiện trong 
bảng 11. 
Bảng 11 cho thấy ứng viên 5 là lựa chọn tốt 
nhất cho vị trí kế toán của công ty dựa trên 
phân tích mức độ ảnh hưởng của 8 tiêu chí nói 
trên mặc dù GPA bậc đại học (tiêu chí C3) của 
ứng viên 5 chỉ xếp hạng thứ 3 trong số 9 ứng 
viên hay đối với tiêu chí C2 và C8 
thì ứng viên 5 
xếp sau ứng viên 6. Điều này cho thấy việc xác 
định trọng số của các tiêu chí đóng vai trò quan 
trọng trong việc xếp hạng các ứng viên. Các ứng 
viên 6 và 2 lần lượt được xếp ở vị trí thứ 2 và 3, 
Mô hình MOORA dựa vào entropy mờ mới ứng dụng cho hệ thống thông tin tuyển dụng 
984 
ứng viên 9 ở cuối bảng xếp hạng. Kết quả xếp 
hạng các ứng viên cũng phù hợp với số liệu 
thông tin ở bảng 7. 
3.2.2. Sử dụng phương pháp FMCDM dựa 
vào độ đo khoảng cách giữa các tập mờ 
Áp dụng các bước tính toán như trong phần 
2.3 với phương án P* = (0, 1, 1,, 1) và ma trận 
thông tin đã mờ hóa như trong (8) ta thu được 
kết quả ở bảng 12. Kết quả này cho thấy ứng 
viên 5 là lựa chọn thích hợp nhất cho ví trí kế 
toán của doanh nghiệp khi xem xét đồng thời 8 
tiêu chí. Ứng viên 1 ở cuối bảng xếp hạng. 
Bên cạnh đó, để so sánh, đánh giá khách 
quan về kết quả theo phương pháp đề xuất thì 
chúng tôi so sánh kết quả thu được với kết quả 
của phương pháp SWARA, kết quả được thể 
hiện trong hình 4. Từ hình 4 cho thấy các kết 
quả thu được từ phương pháp FMOORA dựa 
vào độ đo entropy mờ mới, FMCDM dựa vào độ 
đo khoảng cách giữa các tập mờ và phương 
pháp SWARA cơ bản là như nhau. Cả 3 phương 
pháp đều cho kết quả ứng viên 5 là lựa chọn tốt 
nhất, tiếp theo là các ứng viên 6 và 2. Tuy 
nhiên, đối với ứng viên 4 và 7 kết quả xếp hạng 
có sự khác nhau giữa 3 phương pháp, cụ thể 
đối với phương pháp FMOORA dựa vào độ đo 
entropy mờ mới và SWARA thì ứng viên 4 được 
xếp thứ 5 và ứng viên 7 được xếp thứ 4. Với 
phương pháp FMCDM, ứng viên 4 xếp thứ 4 và 
ứng viên 7 xếp thứ 5 trong bảng xếp hạng các 
ứng viên. 
 Bảng 8. Ma trận thông tin đã mờ hóa 
 C1 C2 C3 C4 C5 C6 C7 C8 
Ứng viên 1 0,5000 0,6500 0,0000 0,5000 0,3333 0,6666 0,3333 0,2857 
Ứng viên 2 0,6667 0,4000 0,5000 0,9167 0,8333 0,3333 0,6667 0,4286 
Ứng viên 3 0,3333 0,3867 0,3333 0,5000 0,3333 0,1667 0,3333 0,1429 
Ứng viên 4 0,6667 0,3933 0,3333 0,8333 0,6667 0,5000 0,5000 0,2857 
Ứng viên 5 0,5000 0,5600 0,6667 0,6667 0,6667 0,5000 0,6667 0,7143 
Ứng viên 6 0,6667 0,7500 0,8333 0,8333 0,5000 0,3333 0,6667 0,7143 
Ứng viên 7 0,3333 0,4600 0,6667 0,4167 0,8333 0,3333 0,1667 0,4286 
Ứng viên 8 0,5000 0,3933 0,3333 0,1667 0,5000 0,3333 0,3333 0,2857 
Ứng viên 9 0,3333 0,4267 0,3333 0,3333 0,3333 0,1667 0,1667 0,1429 
Bảng 9. Entropy mờ và trọng số của các tiêu chí 
 C1 C2 C3 C4 C5 C6 C7 C8 
Entropy 0,9259 0,9372 0,7654 0,7469 0,8395 0,8395 0,8271 0,7800 
Trọng số 0,0553 0,0468 0,1752 0,1891 0,1199 0,1199 0,1291 0,1643 
Bảng 10. Ma trận thông tin 
 C1 C2 C3 C4 C5 C6 C7 C8 
Ứng viên 1 0,0276 0,0304 0,0000 0,0945 0,0399 0,0799 0,0430 0,0469 
Ứng viên 2 0,0369 0,0187 0,0876 0,1733 0,0999 0,0399 0,0861 0,0704 
Ứng viên 3 0,0184 0,0181 0,0584 0,0945 0,0399 0,0199 0,0430 0,0234 
Ứng viên 4 0,0369 0,0184 0,0584 0,1575 0,0799 0,0599 0,0645 0,0469 
Ứng viên 5 0,0276 0,0262 0,1168 0,1260 0,0799 0,0599 0,0861 0,1173 
Ứng viên 6 0,0369 0,0351 0,1460 0,1575 0,0599 0,0399 0,0861 0,1173 
Ứng viên 7 0,0184 0,0215 0,1168 0,0787 0,0999 0,0399 0,0215 0,0704 
Ứng viên 8 0,0276 0,0184 0,0584 0,0315 0,0599 0,0399 0,0430 0,0469 
Ứng viên 9 0,0184 0,0200 0,0584 0,0630 0,0399 0,0199 0,0215 0,0234 
Nguyễn Hữu Hải, Nguyễn Văn Hạnh, Vũ Thị Thu Giang, Đỗ Thị Huệ, Nguyễn Thị Bích Thủy 
985 
Bảng 11. Chỉ số Pi, Ri, chỉ số ưu tiên Qi và kết quả xếp hạng các ứng viên 
 Pi Ri Qi Xếp hạng 
Ứng viên 1 0,0478 0,0138 0,0340 6 
Ứng viên 2 0,0823 0,0184 0,0639 3 
Ứng viên 3 0,0425 0,0092 0,0333 7 
Ứng viên 4 0,0694 0,0184 0,0510 5 
Ứng viên 5 0,0875 0,0138 0,0737 1 
Ứng viên 6 0,0917 0,0184 0,0733 2 
Ứng viên 7 0,0641 0,0092 0,0549 4 
Ứng viên 8 0,0426 0,0138 0,0288 8 
Ứng viên 9 0,0352 0,0092 0,0260 9 
Bảng 12. Xếp hạng các ứng viên theo FMCDM 
 d(Ai, P
*
) Xếp hạng 
Ứng viên 1 0,6708 6 
Ứng viên 2 0,4596 3 
Ứng viên 3 0,6810 7 
Ứng viên 4 0,5334 4 
Ứng viên 5 0,3667 1 
Ứng viên 6 0,3856 2 
Ứng viên 7 0,5510 5 
Ứng viên 8 0,6818 8 
Ứng viên 9 0,7284 9 
Hình 4. Kết quả xếp hạng ứng viên theo FMOORA, FMCDM và SWARA
4. KẾT LUẬN 
Trong bài báo này chúng tôi đã nghiên cứu 
và đề xuất độ đo entropy mới của tập mờ nhằm 
cải thiện cách xác định trọng số của các tiêu chí 
trong phương pháp FMOORA, một nhân tố đóng 
vai trò quan trọng trong bài toán MCDM. 
Chúng tôi đã áp dụng mô hình đề xuất để giải 
quyết bài toán thực tế như là lựa chọn nhân sự 
cho khóa tập huấn của công ty và nhân sự kế 
toán cho doanh nghiệp ngành thép và vật liệu 
công nghiệp. Qua hai ví dụ đã phân tích ở trên 
cho thấy trọng số của các tiêu chí ảnh hưởng lớn 
đến kết quả xếp hạng của các ứng viên. Do vậy, 
việc xây dựng một phương pháp xác định trọng 
số của các tiêu chí trong bài toán MCDM là cần 
thiết. Độ đo entropy mờ mới đã thể hiện được sự 
hiệu quả của nó trong việc xác định trọng số của 
các tiêu chí trong phương pháp FMOORA. Từ 
đó, mô hình đề xuất cho chúng ta kết quả xếp 
Mô hình MOORA dựa vào entropy mờ mới ứng dụng cho hệ thống thông tin tuyển dụng 
986 
hạng các ứng viên chính xác hơn. Ngoài ra, độ 
đo entropy mờ được đề xuất cung cấp cho chúng 
ta nhiều lựa chọn hơn để tính độ đo entropy của 
tập mờ. Trong tương lai, độ đo entropy được đề 
xuất cần được tiếp tục nghiên cứu và ứng dụng 
để giải quyết các bài toán khác nhau như là bài 
toán ra quyết định nhóm, bài toán phân cụm dữ 
liệu mờ và nhận dạng mẫu. 
TÀI LIỆU THAM KHẢO 
Ali R.A., Milan N. & Zahra A. (2017). Personnel 
selection using Group fuzzy AHP and SAW 
methods. Journal of engineering management and 
competitiveness (JEMC). 7(1): 3-10. 
Brauers W.K.M. & Zavadskas E.K. (2006). The 
MOORA method and its application to priva-
tization in a transition economy. Control and 
Cybernetics. 35(2): 445-469. 
Brauers W.K.M. & Zavadskas E.K. (2010). Project 
management by MULTIMOORA as an instrument 
for transition economies. Techn-ological and 
Economic Development of Economy. 16(1): 5-24. 
El-Santawy M.F. (2012). Personnel Training Selection 
Problem Based on Modified TOPSIS". Computing 
and Information Systems Journal. University of the 
West of Scotland. 16(1): 92-97. 
Gökay Akkaya, Betül Turanoðlu & Sinan Öztas (2015) 
An Integrated Fuzzy AHP and Fuzzy MOORA 
Approach to the problem of Industrial Engineering 
Sector Choosing. Expert Systems with Applications. 
Hadad Y., Keren B. & Laslo Z. (2013). A 
decisionmaking support system module for project 
manager selection according to past performance. 
International Journal of Project Management. 
31(4): 532-541. 
Hwang C.L. & Yoon K. (1981). Multiple Attributes 
Decision Making Methods and Applications. 
Heidelberg: Springer, Berlin. 
Kabak M., Burmaoðlu S. & Kazançoðlu Y. (2012). A 
fuzzy hybrid MCDM approach for professional 
selection. Expert Systems with Applications. 
39(3): 3516-3525. 
Karande P. & Chakraborty S. (2012). A Fuzzy-
MOORA approach for ERP system selection. 
Decision Sciences Letters 1(1): 11-22. 
Kersuliene V. & Turskis Z. (2011). Integrated fuzzy 
multiple criteria decision making model for 
architect selection. Technological and Economic 
Development of Economy. 17(4): 645-666. 
Kersuliene V., Zavadskas E.K. & Turskis Z. (2010). 
Selection of rational dispute resolution method by 
applying new step - wise weight assessment ratio 
analysis (SWARA). Journal of Business 
Economics and Management. pp. 243-258. 
Liu Xuecheng (1992). Entropy, distance measure and 
similarity measure of fuzzy sets and their relations. 
Fuzzy Sets and Systems. 52: 305-318. 
Luis P.D., Luis A.R.P., Alejandro A.I., David L.C. & 
Zeshui X. (2018) MOORA under Pythagorean 
Fuzzy Set for Multiple Criteria Decision Making. 
Complexity in Manufacturing Processes 
and Systems. 
Mohamed F. El-Santawy1 & Ahmed A.N. (2012). 
Personnel Training Selection Problem Based on 
SDV-MOORA. Life Science Journal. 9(2s). 
Petrovic-Lazarevic S. (2001). Personnel selection fuzzy 
model. International Transactions in Operational 
Research. pp. 89-105. 
Saaty T.L. (1980). The analytic hierarchy process. 
New York: McGraw-Hill. 
Saaty T.L. (1996). The Analytic Network Process. 
RWS Publications, Pittsburgh. 
Stanujkic D., Magdalinovic N., Jovanovic R. & 
Stojanovic S. (2012). An objective multi-criteria 
approach to optimization using MOORA method and 
interval grey numbers. Technological and Economic 
Development of Economy. 18(2): 331-363. 
Stanujkic D., Magdalinovic N., Milanovic D., 
Magdalinovic S. & Popovic G. (2014). An 
Efficient and Simple Multiple Criteria Model for a 
Grinding Circuit Selection Based on MOORA 
Method. Informatica. pp. 73-93. 
Wang D. (2009). Extension of TOPSIS Method for R 
and D Personnel Selection Problem with Interval 
Grey Number. 2009 International Conference on 
Management and Service Science. pp. 1-4. 
Yakup Çelikbilek (2018). Using an Integrated Grey 
AHP–MOORA Approach for Personnel Selection: 
An Application on Manager Selection in the Health 
Industry (2015). Alphanumeric journal. 6(1). 
Zadeh L.A. (1965). Fuzzy sets. Information and 
control. 8(3): 338-353. 
Zhang S.F. & Liu S.Y. (2011). A GRA-based 
intuitionistic fuzzy multi-criteria group decision 
making method for personnel selection, Expert 
Systems with Applications. pp. 11401-11405.