Mô hình động lực học của máy kéo với rơ mooc một trục vận chuyển gỗ

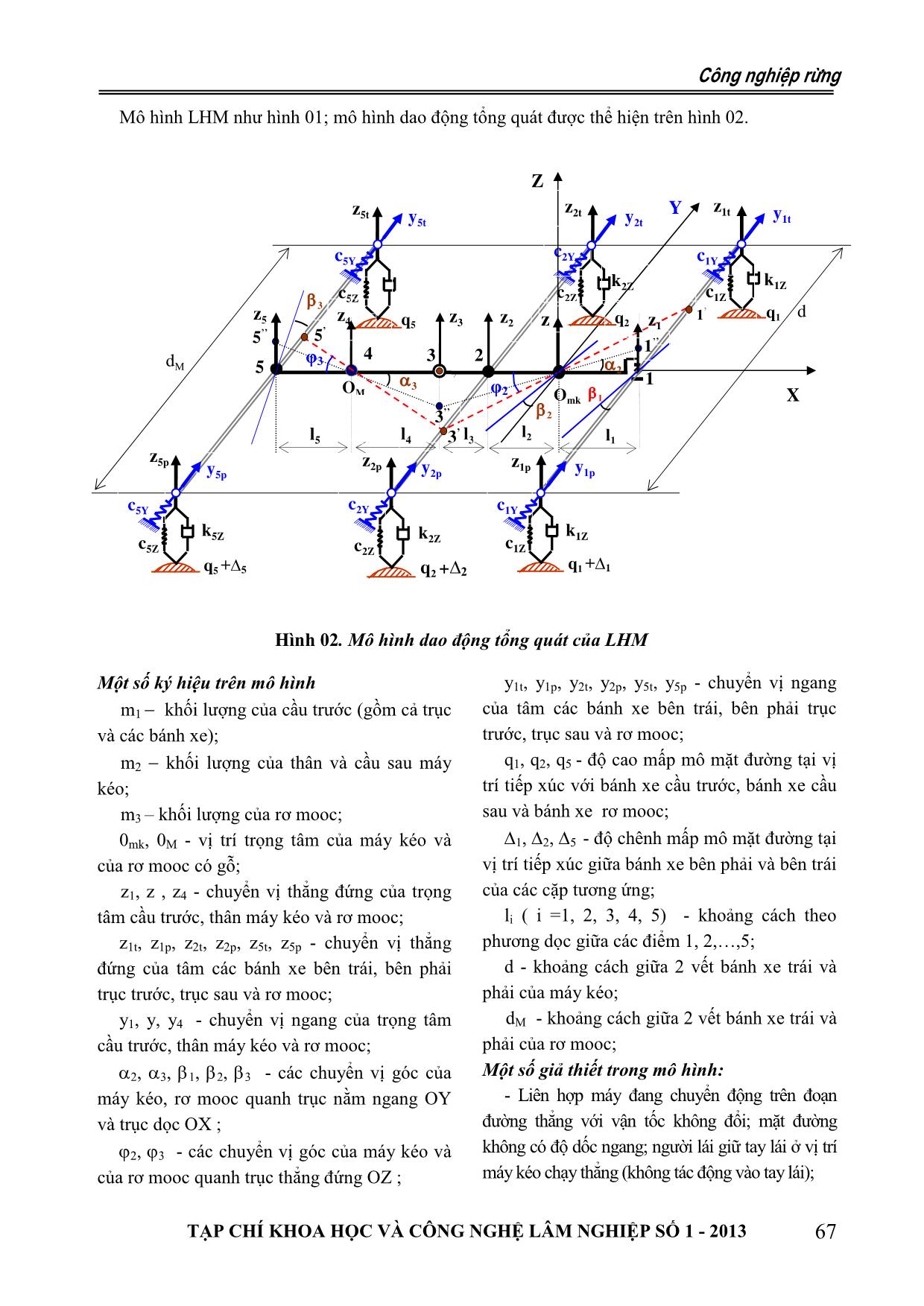
g thức (1) để tìm PTVP chuyển động của hệ 
III. KẾT QUẢ NGHIÊN CỨU 
 LHM có 6 chuyển vị. Tuỳ mục đích nghiên 
3.1. Xây dựng mô hình động lực học tổng 
 cứu mà có thể xem xét các chuyển vị này đồng 
quát cho liên hợp máy 
 thời hay độc lập (hình 02). 
Lựa chọn mô hình nghiên cứu 
 Kết quả nghiên cứu của một số tác giả 
 Liên hợp máy gồm máy kéo bánh hơi và [1], [7], [8] đã chỉ ra rằng với các liên hợp 
rơ mooc một trục (LHM) là một hệ cơ học máy gồm máy kéo bánh hơi và rơ mooc thì 
biến dạng. Đặc trưng cho sự biến dạng là các dao động thẳng đứng và dao động quanh 
biến dạng của các phần tử đàn hồi thông qua trục dọc là có ảnh hưởng trực tiếp đến áp lực 
các bánh lốp, nhíp, các khớp, khung, vỏ động của các cặp bánh xe lên mặt đất và 
xe. Nếu gắn vào thân máy kéo một hệ toạ chúng ảnh hưởng nhiều nhất đến điều kiện ổn 
độ đi qua trọng tâm của nó thì có thể biểu thị định của chuyển động. Mặt khác các dịch 
sự biến dạng của hệ thống theo cả 3 phương chuyển theo phương ngang và quay quanh 
OX, OY, OZ. Với các biến dạng đó LHM trục thẳng đứng của chúng là biểu hiện cụ thể 
được coi như một hệ đàn hồi. Hệ này chuyển của sự lệch hướng chuyển động của LHM. 
động trên đường đối với hệ trục cố định Tác giả xây dựng mô hình nghiên cứu các 
OX0Y0Z0. Các dịch chuyển của LHM theo dao động của liên hợp máy gồm máy kéo bánh 
các trục đó gây nên các chuyển vị dọc theo 3 hơi với rơ mooc một trục chở gỗ, chuyển động 
trục và quay quanh 3 trục, như vậy có thể coi thẳng trên mặt đường mấp mô, làm cơ sở khảo 
trong hệ không gian 3 chiều chuyển động của sát tính ổn định chuyển động của nó. 
66 TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ LÂM NGHIỆP SỐ 1 - 2013 
 C«ng nghiÖp rõng 
 Mô hình LHM như hình 01; mô hình dao động tổng quát được thể hiện trên hình 02. 
 Z 
 z z2t Y z1t 
 5t y y y1t 
 5t 2t 
 c
 c5Y 2Y c1Y 
 k k1Z 
 2Z 
 c5Z c2Z c1Z 
 3 
 ’
 z5 z z 1 q1 d 
 4 q5 3 z2 z q2 z1 
 5’’ 5’ 
 1’’ 
 d φ3 4 3 2 
 M 5 2 
 3 1 
 OM φ2 
 O 1 X 
 mk 
 3’’ 2 
 ’ l
 l5 l4 3 l3 2 l1 
 z
 5p z2p z1p 
 y5p y2p y1p 
 c5Y c2Y c1Y 
 k5Z k2Z k1Z 
 c5Z c2Z c1Z 
 q +∆1 
 q5 +∆5 q2 +∆2 1 
 Hình 02. Mô hình dao động tổng quát của LHM 
Một số ký hiệu trên mô hình y1t, y1p, y2t, y2p, y5t, y5p - chuyển vị ngang 
 m1 khối lượng của cầu trước (gồm cả trục của tâm các bánh xe bên trái, bên phải trục 
và các bánh xe); trước, trục sau và rơ mooc; 
 m2 khối lượng của thân và cầu sau máy q1, q2, q5 - độ cao mấp mô mặt đường tại vị 
kéo; trí tiếp xúc với bánh xe cầu trước, bánh xe cầu 
 m3 – khối lượng của rơ mooc; sau và bánh xe rơ mooc; 
 0mk, 0M - vị trí trọng tâm của máy kéo và 1, 2, 5 - độ chênh mấp mô mặt đường tại 
của rơ mooc có gỗ; vị trí tiếp xúc giữa bánh xe bên phải và bên trái 
 z1, z , z4 - chuyển vị thẳng đứng của trọng của các cặp tương ứng; 
tâm cầu trước, thân máy kéo và rơ mooc; li ( i =1, 2, 3, 4, 5) - khoảng cách theo 
 z1t, z1p, z2t, z2p, z5t, z5p - chuyển vị thẳng phương dọc giữa các điểm 1, 2,,5; 
đứng của tâm các bánh xe bên trái, bên phải d - khoảng cách giữa 2 vết bánh xe trái và 
trục trước, trục sau và rơ mooc; phải của máy kéo; 
 y1, y, y4 - chuyển vị ngang của trọng tâm dM - khoảng cách giữa 2 vết bánh xe trái và 
cầu trước, thân máy kéo và rơ mooc; phải của rơ mooc; 
 2, 3, 1, 2, 3 - các chuyển vị góc của Một số giả thiết trong mô hình: 
máy kéo, rơ mooc quanh trục nằm ngang OY - Liên hợp máy đang chuyển động trên đoạn 
và trục dọc OX ; đường thẳng với vận tốc không đổi; mặt đường 
 2, 3 - các chuyển vị góc của máy kéo và không có độ dốc ngang; người lái giữ tay lái ở vị trí 
của rơ mooc quanh trục thẳng đứng OZ ; máy kéo chạy thẳng (không tác động vào tay lái); 
 TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ LÂM NGHIỆP SỐ 1 - 2013 67
C«ng nghiÖp rõng 
 - Không kể đến sự trượt của các bánh xe; xe là vật cứng; 
 - Khối lượng của máy kéo và rơ móc quy - Các bánh hơi có độ cứng theo các phương 
đổi về trọng tâm của chúng; là cz , cy có độ lớn không đổi và bánh xe có 
 - Gỗ được xếp trên rơmooc là một khối đặc, biến dạng nhỏ, làm việc trong giới hạn đàn hồi 
như một vật rắn; (tuyến tính); 
 - Bỏ qua biến dạng của mặt đường tại điểm - Các dịch chuyển được xét là những dao 
tiếp xúc với các bánh xe; động nhỏ quanh vị trí cân bằng tĩnh của hệ. 
 - Bỏ qua các lực cản không khí và áp lực 
 Một số phương trình liên kết 
của gió, vì vận tốc của LHM thấp; 
 - Liên kết giữa các bánh xe với mặt đường Trong thực tế chuyển vị của các điểm so với 
là giữ, dừng; vị trí cân bằng tĩnh là nhỏ, có thể coi: Sin j 
 - Không tính đến ảnh hưởng của góc đặt j, Cos j 1; Sinj j, Cosj 1; 
bánh xe; Sinφj φj, Cosφj 1 (j = 1, 2, 3). 
 - Bỏ qua ma sát ở khớp nối giữa máy kéo và Từ các quan hệ hình học ta xác định được 
rơ moóc; ma sát các ổ trục của các bánh xe; các phương trình liên kết: 
 - Khung máy kéo, rơ moóc và các trục bánh 
 x1 xl;x 1 2 xl;x 2 5 x(l 2 l 3 l 4 l) 5
 z1 zl 1 2 ;z 2 zl 2 2 ;z 3 z(l 2 l) 3 2
 z4 z(l 232435 l) l ;z z(l 232453 l) (l l)
 y1 yl;y 122 yl 224 ;y y(l 23243 l) l
 y5 y ( l 2 l 3 ) 2 ( l 4 l 5 ) 3
 d d
 z z i  ; z z i  (2 )
 it i2 i ip i 2 i
 d d
 y y i ; y y i 
 it i2 i ip i 2 i
 Gọi it, ip ( i = 1, 2, 5) là các biến dạng tổng quát có dạng như công thức (1): 
theo phương thẳng đứng và phương ngang của d  T  T   
 Q 
các phân tử đàn hồi (bánh xe bên trái và bánh k
 dt  qk  q k  q k  q  k 
xe bên phải). Theo quan hệ biến dạng ta có các 
 k = 1, 2, ..., 9 
thành phần chuyển vị: 
 T- hàm động năng của hệ, gồm: động năng 
 zit q i  it của cầu trước, thân máy kéo và rơ mooc. 
 với i=1,2,5 (3) 
 z q 
 ip i i ip T= Tct+ Tmk+ Tm 
3.2. Thành lập phương trình vi phân dao ,  - hàm thế năng và hàm hao tán của hệ 
động của LHM qk các toạ độ suy rộng (k= 1, 2, 3, , 9): 
 PTVP dao động của hệ này được thiết theo q1 = z; q2 = 2 ; q3= 2 ; q4 = 1 ; q5 = 3 ; q6 = 
phương trình Lagrangiơ loại II. 3 ; q7 = y; q8 = 2 ; q9 = 3 . 
 Phương trình Lagrangiơ loại II viết dạng 
68 TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ LÂM NGHIỆP SỐ 1 - 2013 
 C«ng nghiÖp rõng 
 Qk lực suy rộng tương ứng với toạ độ h0 2 
 q (1 C os S ) Khi 0 SS 0 ; 
suy rộng thứ k. 2 S0
 Để lập PTVP dao động của LHM theo 
 Q = 0, khi S > S0 
phương trình Lagrangiơ loại II ta có nhận xét 
 Trong đó: h0 - chiều cao mấp mô mặt 
khi các bánh xe di chuyển trên bề mặt của mấp 
 đường; S0 - chiều dài sóng mặt đường 
mô do sự chênh lệch độ cao giữa 2 bánh ở mỗi 
cặp làm phát sinh lực ngang. Lực này không Động năng của hệ 
chỉ gây biến dạng cho lốp mà còn đẩy cả trọng Hệ khảo sát có 3 vật rắn hợp thành nên: 
tâm bánh xe dịch chuyển theo phương ngang 
 T = TC1 + TTmk M 
và gây mô men quay khung máy kéo quanh 
 Trong đó: T - Động năng của cầu trước, 
trục OZ. Từ đó khi áp dụng phương trình C1
 có trọng tâm tại điểm 1; 
Lagrangiơ II cho các toạ độ suy rộng y, 2, 3 
 T - Động năng của thân máy kéo, có 
có tính đến lực suy rộng và mô men kể trên. mk
 Bài toán xét với mặt đường có các chướng trọng tâm tại Omk; 
ngại vật đơn với quy luật biến đổi chiều cao TM - Động năng của rơ mooc có gỗ, có 
của vật cản q (s), có dạng: trọng tâm tại OM. 
 Động năng của các phần được tính theo dạng chuyển động của chúng như sau: 
 1 1 1 
 T m (z2 x 2 y 2 ) J 2 J 2 ; 
 c12 1 1 1 1 21x 1 2 1z 2
 Với: y1 y l 1  2 ; m1 m 1t m 1p - Tổng khối lượng của cầu trước. 
 1 1 1 1
 T = m (z2 x  2 y 2 ) J  2 J  2 J  2 ; 
 mk 22 2 2y 2 2 2x 2 2 2z 2
 2 2 2
 12 2 1 1 1 2
 T = m (z4 x y ) J 3 J  J  . 
 M 23 4 4 2 3y 2 3x3 2 3z 3
 Với y4 y (l 2 l 3 ) 2 l 4 3 
 Thay các đại lượng z1, z5 và y1, y5 từ (2) vào các biểu thức tính động năng ta có động năng của 
hệ sẽ là: 
 1 2 2
 T A(zx)Az 2 Az 3 A 2 3
 2 1 z 2 z 3 z 4 z
 2 2 2 2 2
 12 1 1 1 1 1
 A5z2 A 6z 3 A 7z 1 A 8z  2 A 9z  3 A 1y y 
 2 2 2 2 2 2
 1 1 
 (A A)yA A 2 A. 2 (4)
 2y2 3y3 5y232 4y2 2 6y3
 Trong đó Ai(z,y) là các hệ số được đặt 
 C«ng nghiÖp rõng 
Thế năng của hệ 
 Khi xét dao động của hệ quanh vị trí cân bằng tĩnh ta không cần tính đến thế năng của 
 TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ LÂM NGHIỆP SỐ 1 - 2013 69
lực trọng trường, chỉ tính thế năng của các lực đàn hồi ở các bánh hơi. 
 12 2 1 2 2 1 2 2
  c1z  1t  1p c 2z  2t  2p c 5z  5t  5p 
 2 2 2 
 1 1 1
 c (2  2 ) c (  2  2 ) c (  2  2 ).
 21y 1yp 1yt 2 2y 2yp 2yt 2 5y 5yp 5yt
 Trong đó: c1z ,c 1y ; c2z ,c 2y ; c5z ,c 5y - độ cứng của các bánh xe trên trục 1, 2 và 5 theo phương 
đứng và phương ngang 
 it , ip - Biến dạng đàn hồi của các bánh xe bên trái và bên phải ở trục thứ i 
 ( i = 1, 2, 5), chúng được xác định theo các chuyển vị tương ứng . 
 Từ các phương trình liên kết (2) và (3) ta có hàm thế năng của hệ: 
 2 2 2 2 2 2
  B1z z B 2z 2 B 3z 3 B 4z  1 B 5z  2 B 6z  3 
 B7z z 2 B 8z z 3 B 9z z B 10z2 B 11z3 B 12z23 
 2 (5) 
 B13z1 B 14z2  B 15z3  B 16z ByByBy 1y 2y 2 3y 3 
 2 2
 B4y2 B 5y23 B 6y3 B 7y
 Trong đó Bi(z,y) là các hệ số được đặt 
Hàm hao tán 
 Hàm hao tán của hệ được xác định theo hệ số cản chuyển dịch của các bánh hơi k1z, k2z và k5z ; 
bỏ qua hệ số cản ngang của lốp: 
 1 2 2 1 2 2 1 2 2 
  k1z  1 t  1 p k 2 z  2 t  2 p k 5 z  5 t  5 p 
 2 2 2 
 22 2 2
 1 1 
 1 2 
 k1z 1t q1 1 p q k 2 z 2 t q 2 2 p q 
 2 z z1 2 z z 2
 2 2
 1 
 5 
 k5z 5t q5 5 p q 
 2 z z 5
 Thay các biểu thức zit và zip từ (3) vào và biến đổi, ta có: 
 2 2 2 2 2 2 
  DzD1 2 2 D 3 3 D 4 1 D 5  2 D 6  3 DzDz 7 2 8 3 
 (6) 
 D9 z D 10 2 D 11 3 D 12 2 3 D 13 1 D 14  2 D 15  3 D 16
 Trong đó Di là các hệ số được đặt: 
 Từ các phương trình liên kết từ (2), (3) tính được động năng (4), thếC«ng năng nghiÖp (5), hàm rõng 
hao tán (6). Đưa các biểu thức động năng, thế năng và hàm hao tán, các lực và mô men 
70 TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ LÂM NGHIỆP SỐ 1 - 2013 
suy rộng vào công thức (1), qua các phép trình vi phân dao động tổng quát (7) của liên 
biến đổi toán học, xác định được hệ phương hợp máy như sau: 
 1) Az A 2 A 3 2D z D 2 D 3 2B z B 2 B 3 B D
 1z 2z 3z 1 7 8 1z 7z 8z 9z 9
 2) A2zz A 5z 2 A 4z 3 D 7 z 2D 2 2 D 12 3 B 7z z 2B 2z 2 B 12z 3 B 10z D 10
 3) A3zz -A 4z 2 A 6z 3 D 8z z D 12 2 2D 3 3 B 8z z -B 12z 2 2B 3z 3 B 11z D 11
 4) A 2D  2B  B D
 7z1 4 1 4z 1 13z 13
 5) A 2D  2B  B D (7)
 8z2 5 2 5z 2 14z 14
 6) A9z3 2D 6  3 2B 6z  3 B 15z D 15
 tg1 tg  2 tg 5
 7)AyAA1y 22331 y  y  2 ByBBZ y 22331 y y Z 2 Z 5 ;
 cos1 cos  2 cos5
 8)A y A  A  B y 2 B B 
 2y 4 y 2 5 y 3 2 y 4 y 2 5 y 3
 tg tg  tg  d d
 Zl1 Zl 2 .(1 Z 2 )( Ztgtg   ) Ztg .(  tg  ).;
 11cos 22 cos  22 cos  111p t 2 222 p t 2
 1 2 2
 tg 5 tg 5
 (9)AyA3y 52633 y  A y  ByB y 52 y 2 B 63545 y Zll ( ) 5.Z 5 (1 ) 
 cos cos
 5 5 
 dM
 Z5.( tg 5p tg  5 t ). .
 2
 Hệ phương trình vi phân (7) là hệ 9 phương lệch chiều cao mấp mô mặt đường giữa các bánh 
trình vi phân tuyến tính không thuần nhất có hệ xe bên trái và bên phải ( i 0; i=1, 2, 5). 
số phụ thuộc vào các thông số của liên hợp + Các dao động ngang theo phương OY và 
máy và dạng mấp mô mặt đường. Đó là hệ quay quanh trục thẳng đứng OZ được thể hiện 
phương trình vi phân biểu diễn dao động theo qua 3 phương trình 7,8,9 trong hệ (7), phụ 
các phương và quay quanh 3 trục OX, OY, OZ thuộc vào mức chênh độ cao giữa các bánh xe 
của máy kéo và rơ mooc chở gỗ do tác động trong mỗi cầu khi chuyển động trên đường 
động học của độ mấp mô mặt đường . mấp mô. 
 + Từ hệ phương trình vi phân lập được (7) ta Hệ PTVP (7) là cơ sở để khảo sát tính ổn định, 
nhận thấy các dao động thẳng đứng của máy kéo các dao động của liên hợp máy thông qua lập 
 phương trình đặc trưng, giải hệ phương trình vi 
và dao động quanh trục nằm ngang của thân máy 
 phân, xác định ảnh hưởng của độ mấp mô mặt 
kéo, rơ mooc liên quan chặt chẽ với nhau được 
 đường đến các đặc trưng động lực học của LHM 
thể hiện qua 3 phương trình 1, 2, 3. 
 như biên độ dao động cực đại, gia tốc rung cực đại 
 + Các dao động quay quanh trục dọc OX được của máy kéo theo các phương thẳng đứng và nằm 
thể hiện bằng 3 phương trình 4, 5, 6 trong hệ (7), ngang; ảnh hưởng của sự không đồng phẳng của 
dao động của cơ hệ chỉ tồn tại khi có độ chênh mặt đường đến quỹ đạo chuyển động của LHM.... 
 TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ LÂM NGHIỆP SỐ 1 - 2013 72
 C«ng nghiÖp rõng 
IV. KẾT LUẬN trình động lực học máy (Tài liệu dịch từ tiếng Đức). 
 NXB Khoa học Kỹ thuật, Hà Nội. 
 Sử dụng phương pháp giải tích để xây dựng 
 2. Nguyễn Văn Đạo (2002), Cơ học giải tích, NXB 
mô hình và thành lập phương trình vi phân ĐHQG Hà Nội. 
chuyển động của trọng tâm máy kéo khi vượt 3. Đặng Thế Huy (1995), Một số vấn đề về cơ học 
qua mấp mô, đã thiết lập được mô hình động giải tích và cơ học máy, Trường Đại học Nông nghiệp 1, 
lực học và hệ phương trình vi phân chuyển Hà Nội. 
động tổng quát (7) cho loại máy kéo bánh hơi 4. Nguyễn Văn Khang (2007), Động lực học hệ nhiều vật, NXB 
có rơ mooc một trục vận chuyển gỗ khi di KHKT, Hà Nội. 
chuyển trên đường có mấp mô theo cả 3 5. Lê Tấn Quỳnh (2006), Nghiên cứu lựa chọn công 
 nghệ và hệ thống thiết bị cơ giới hoá các khâu làm đất, 
phương OX, OY, OZ . Hệ phương trình này 
 trồng, chăm sóc rừng và khai thác gỗ, Báo cáo khoa 
cho phép nghiên cứu động lực học tổng thể dao 
 học và kỹ thuật đề tài cấp nhà nước KC07-26, Tháng 
động theo phương thẳng đứng, phương nằm 10/2006. 
ngang và quỹ đạo chuyển động của liên hợp 6. William F Riley, Leroy D Sturges (1993), 
máy, là cơ sở để khảo sát động lực học chung Engineering Mechanics Dynamics, John Wiley & Sons, 
cho loại thiết bị này, là cơ sở để thiết kế cải INC, New York. 
tiến máy, rơ mooc; góp phần bổ sung lý thuyết 7. Александров. В. А, (1995), Моденлирование 
chung về động lực học ô tô, máy kéo. Технологических Про-цессов Лесных Машин, 
 Издательство “Экология”, Москва. 
TÀI LIỆU THAM KHẢO 8. Гячев . Л.В, (1976), Динамика Машинно- 
 1.Vũ Liêm Chính, Phan Nguyên Di (2001),Giáo Тракторных и Автомо-бильных Агрегатов, 
 Издательство Ростовского Университета. 
 DYNAMICS OF TRACTOR WITH TWO WHEEL TRAILER 
 WHEN TRANSPORTING FOREST TIMBER 
 Pham Minh Duc, Nguyen Van Quan 
 SUMMARY 
 Research on dynamics of tractor trailers transporting wood is the main content of this article.The author established 
 mechanical model; then finding out the general dynamics model to determine the kinetic factors for it. By 
 applying aanalytical mechanics and using Lagranger Equation (type II); dynamic model and general differential 
 Equations were established for motion tractor with two wheel trailer when going through bumpy under all three 
 directions OX, OY, OZ (for survey oscillate vertically, oscillate horizontally and the rotation around the axis). This 
 equations allow us applying the overall dynamics of the fluctuations, as a basis to examine the dynamics to this 
 type of equipment. 
 Keywords: Dynamics of tractor; equations of motion; motion stability; two wheel trailer 
 Người phản biện: TS. Nguyễn Văn Bỉ 
72 TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ LÂM NGHIỆP SỐ 1 - 2013