Máy véc-tơ tựa song sinh và áp dụng

 + 2 = . PSVM sẽ 
tìm hai siêu phẳng song song với lề lớn nhất. GEPSVM [4] có cách tiếp cận khác là tìm 
hai siêu phẳng không nhất thiết song song, mỗi siêu phẳng là gần nhất có thể với một 
lớp và xa nhất có thể với lớp còn lại. 
 푤(1) + (1) = 0;   푤(2) + (2) = 0. (6) 
 Ở đây siêu phẳng 1 của (6) gần nhất với các điểm của lớp 1 và xa nhất với các 
điểm thuộc lớp 2, điều tương tự xảy ra với siêu phẳng 2. Việc tìm siêu phẳng 1 tương 
đương với bài toán tối ưu sau: 
 푤 2
 ‖ 푤 + 푒 ‖2/ ‖[ ]‖
 1 
 min , (7) 
 (푤, )≠0 푤 2
 ‖ 푤 + 푒 ‖2/ ‖[ ]‖
 2 
 1 2
với 푒1 ∈ ℝ ,  푒2 ∈ ℝ là các véc-tơ gồm tất cả tọa độ bằng 1, ‖⋅‖ là chuẩn 퐿2. Ta thấy 
rằng tử số chính là tổng của bình phương khoảng cách tất cả các điểm thuộc lớp 1 tới 
siêu phẳng 1, mẫu số là tổng của bình phương khoảng cách tất cả các điểm thuộc lớp 2 
tới siêu phẳng 1. Đơn giản hóa (7) cho ta: 
 2
 ‖ 푤 + 푒1 ‖
 min 2 , (8) 
 (푤, )≠0 ‖ 푤 + 푒2 ‖
 5 
Máy véc-tơ tựa song sinh và áp dụng 
 Để chính quy hóa (8), ta thêm số hạng chính quy Tikhonov [9] vào tử số, bài 
toán trở thành: 
 푤 2
 ‖ 푤 + 푒 ‖2 + 훿 ‖[ ]‖
 1 
 min 2 , 훿 > 0 (9) 
 (푤, )≠0 ‖ 푤 + 푒2 ‖
 Đặt 
 ≔ [    푒1] [    푒1] + 훿 ,
 { 푤 
 ≔ [    푒 ] [    푒 ],     ≔ [ ] ,
 2 2 
bài toán tối ưu (9) trở thành: 
 min ( ) = , (10) 
 ≠0 
ở đây G, H là các ma trận đối xứng trong 푅(푛+1)×(푛+1). Ta có 
 ( − ( ) )
 ∇ ( ) = 2 , (11) 
hàm ( ) được gọi là thương Rayleigh [1, tr357]. Hàm này có tính chất (휆 ) =
 ( ),   ∀ ,   ∀휆 ≠ 0 do đó (10) tương đương min ( ). Vì ( ) liên tục trên tập compact 
 ∈푆(0, 1)
푆(0,  1) nên đạt cực tiểu và cực đại trên đó. Giả sử ( ) đạt cực tiểu và cực đại tương 
ứng tại min, max. Lúc đó 훻 ( min) = 훻 ( max) = 0 ⇒ min − ( min) min = 0 và 
 max − ( max) max = 0. Như vậy, ( min),    ( max) ∈ [휆1, 휆푛+1] ⇒ ( ) ∈ [휆1, 휆푛+1] 
khi ∈ 푆(0,   1), ở đây 휆1,  휆푛+1 tương ứng là trị riêng nhỏ nhất và lớn nhất của bài toán 
trị riêng suy rộng: 
 = 휆 ,      ≠ 0. (12) 
 Giả sử rằng các cột của ma trận [    푒2] là độc lập tuyến tính, nghiệm toàn cục 
của (10) là véc-tơ riêng của (12) tương ứng với trị riêng nhỏ nhất 휆1. Ký hiệu véc-tơ 
riêng này là (1) thì [푤(1)     (1)] = (1) xác định siêu phẳng 1 trong (6). 
 Bằng cách làm tương tự ta sẽ có được siêu phẳng 2. 
5. MÁY VÉC-TƠ TỰA SONG SINH 
5.1 Trường hợp hai lớp dữ liệu gần tách được tuyến tính 
 Với bài toán như trong mục 4. Ý tưởng của TWSVM cho bài toán phân loại nhị 
phân cũng là đi tìm hai siêu phẳng không song song như GEPSVM, nhưng về mặt 
công thức thì hoàn toàn khác. 
 6 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ, Trường Đại học Khoa học, ĐH Huế Tập 17, Số 1 (2020) 
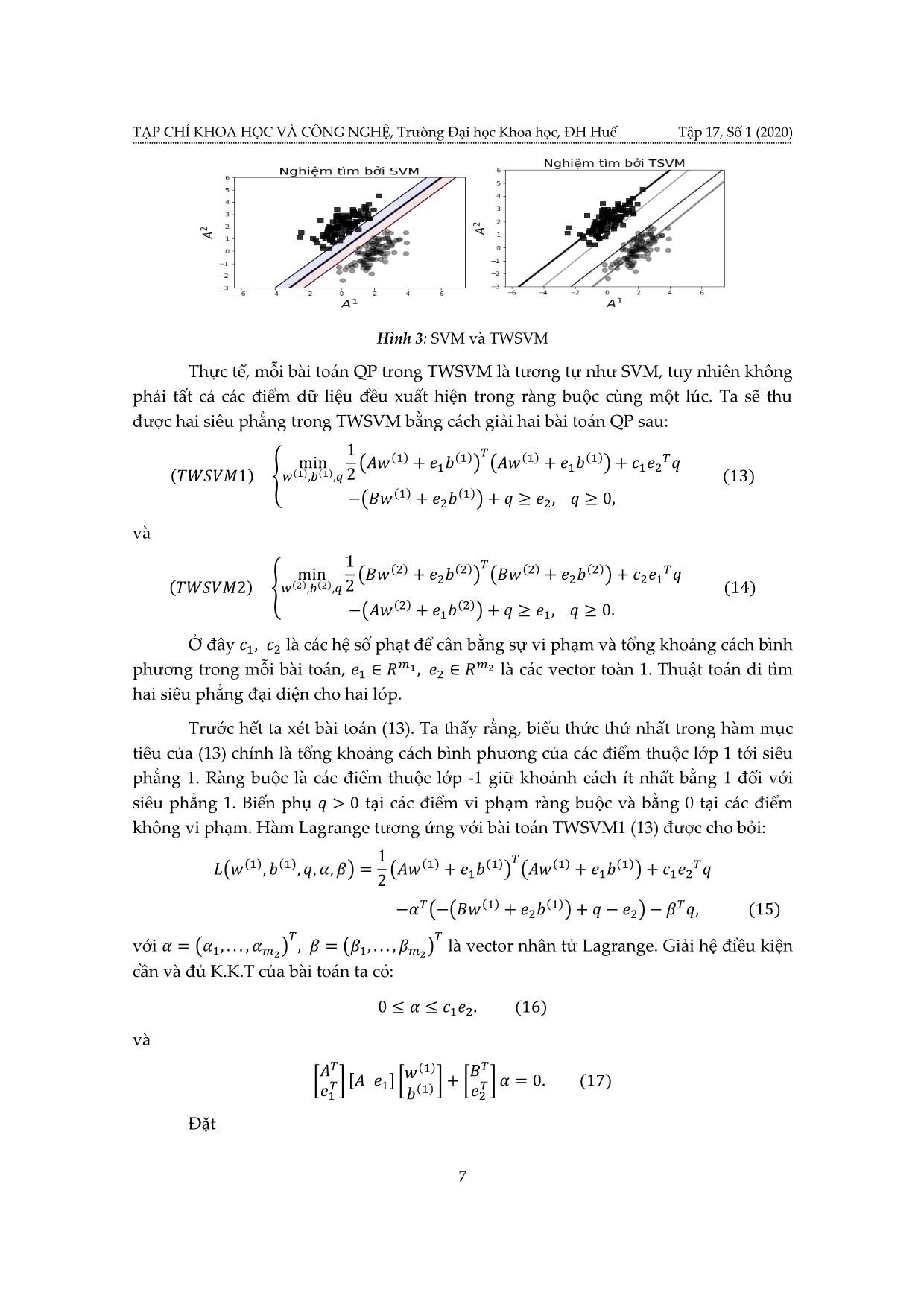
 Hình 3: SVM và TWSVM 
 Thực tế, mỗi bài toán QP trong TWSVM là tương tự như SVM, tuy nhiên không 
phải tất cả các điểm dữ liệu đều xuất hiện trong ràng buộc cùng một lúc. Ta sẽ thu 
được hai siêu phẳng trong TWSVM bằng cách giải hai bài toán QP sau: 
 1 (1) (1) (1) (1) 
 min ( 푤 + 푒1 ) ( 푤 + 푒1 ) + 1푒2 푞
 ( 푊푆 1) {푤(1), (1),푞 2 (13) 
 (1) (1)
 −( 푤 + 푒2 ) + 푞 ≥ 푒2, 푞 ≥ 0,
và 
 1 (2) (2) (2) (2) 
 min ( 푤 + 푒2 ) ( 푤 + 푒2 ) + 2푒1 푞
 ( 푊푆 2) {푤(2), (2),푞 2 (14) 
 (2) (2)
 −( 푤 + 푒1 ) + 푞 ≥ 푒1, 푞 ≥ 0.
 Ở đây 1,   2 là các hệ số phạt để cân bằng sự vi phạm và tổng khoảng cách bình 
 1 2
phương trong mỗi bài toán, 푒1 ∈ 푅 ,  푒2 ∈ 푅 là các vector toàn 1. Thuật toán đi tìm 
hai siêu phẳng đại diện cho hai lớp. 
 Trước hết ta xét bài toán (13). Ta thấy rằng, biểu thức thứ nhất trong hàm mục 
tiêu của (13) chính là tổng khoảng cách bình phương của các điểm thuộc lớp 1 tới siêu 
phẳng 1. Ràng buộc là các điểm thuộc lớp -1 giữ khoảnh cách ít nhất bằng 1 đối với 
siêu phẳng 1. Biến phụ 푞 > 0 tại các điểm vi phạm ràng buộc và bằng 0 tại các điểm 
không vi phạm. Hàm Lagrange tương ứng với bài toán TWSVM1 (13) được cho bởi: 
 1 
 퐿(푤(1), (1), 푞, 훼, 훽) = ( 푤(1) + 푒 (1)) ( 푤(1) + 푒 (1)) + 푒 푞 
 2 1 1 1 2
 (1) (1) 
 −훼 (−( 푤 + 푒2 ) + 푞 − 푒2) − 훽 푞, (15) 
với 훼 = (훼1, . . . , 훼 2 ) ,   훽 = (훽1, . . . , 훽 2) là vector nhân tử Lagrange. Giải hệ điều kiện 
cần và đủ K.K.T của bài toán ta có: 
 0 ≤ 훼 ≤ 1푒2. (16) 
và 
 (1) 
 [ ] 푤
 [ ]    푒1 [ (1) ] + [ ] 훼 = 0. (17) 
 푒1 푒2
 Đặt 
 7 
Máy véc-tơ tựa song sinh và áp dụng 
 푤(1)
 = [    푒1],     = [    푒2],     = [ ], (18) 
 (1)
(17) có thể viết lại thành 
 + 훼 = 0, 
tức là 
 = −( )−1 훼. (19) 
 Để đảm bảo tồn tại ma trận nghịch đảo ( )−1 ta thêm số hạng chính quy 
휖 ,    휖 > 0 như trong [2], với là ma trận đơn vị có số chiều thích hợp, (19) trở thành 
 = −( + 휖 )−1 훼. (20) 
 Tuy nhiên, trong phần sau của bài ta vẫn sử dụng (19) để thuận tiện cho quá 
trình tìm hiểu bài toán, còn khi lập trình thuật toán ta sẽ sử dụng công thức (20). Thay 
vào hàm Lagrange ta thu được bài toán đối ngẫu của TWSVM1 như sau: 
 1 −1 
 max 푒2 훼 − 훼 ( ) 훼
 ( 푊푆 1) { 훼 2 (21) 
 0 ≤ 훼 ≤ 1푒2.
 Bằng cách tương tự, ta xét bài toán TWSVM2 và thu được bài toán đối ngẫu 
sau: 
 1 −1 
 max 푒1 훾 − 훾 ( ) 훾
 ( 푊푆 2) { 훾 2 (22) 
 0 ≤ 훾 ≤ 2푒1.
 푤(2)
và vector 푣 = [ ] được cho bởi 
 (2)
 푣 = ( )−1 훾. (23) 
 Hai ma trận và cùng có cỡ (푛 + 1) × (푛 + 1), trong thực tế số chiều 푛 
là nhỏ hơn nhiều so với số phần tử của hai lớp dữ liệu. Hai siêu phẳng tách đạt được 
là: 
 푤(1) + (1) = 0,    푤(2) + (2) = 0. (24) 
 Với một điểm dữ liệu mới ∈ ℝ푛 ta tính khoảng cách vuông góc từ tới hai 
siêu phẳng, gần siêu phẳng của lớp nào hơn thì thuộc về lớp đó. 
Từ hệ điều kiện K.K.T ta thấy rằng, các điểm thuộc lớp -1 tương ứng với 0 < 훼푖 <
 (1) (1)
 1,   (푖 = 1, . . . , 2) nằm trên siêu phẳng 푤 + = −1, những vector thuộc lớp -1 
này là những vector tựa của lớp 1. Điều tương tự xảy ra với bài toán TWSVM2. 
 Đánh giá độ phức tạp: Quan sát hai bài toán đối ngẫu (21) và (22) thấy rằng các 
ma trận vuông ( )−1 và ( )−1 có cỡ xấp xỉ . Trong bài toán đối ngẫu 
 2
của SVM [3], ma trận vuông có cỡ . Như vậy nếu ta coi độ phức tạp của SVM là 3 
 8 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ, Trường Đại học Khoa học, ĐH Huế Tập 17, Số 1 (2020) 
thì độ phức tạp của TWSVM là xấp xỉ 2( )3, qua đó thấy rằng tốc độ tính toán của 
 2
TWSVM là nhanh hơn SVM xấp xỉ 4 lần. 
5.2 TRƯỜNG HỢP PHI TUYẾN 
 Khi hai lớp dữ liệu là không tách được tuyến tính, tương tự như SVM tiêu 
chuẩn, ta sẽ sử dụng kỹ thuật kernel. Hai mặt phân loại sẽ có dạng: 
 퐾( ,  )푤(1) + (1) = 0,     퐾( ,  )푤(2) + (2) = 0, (25) 
với = [ ] và 퐾 là một kernel nào đó. Bài toán tối ưu có dạng như sau: 
 1 (1) (1) 2 
 min ‖퐾( , )푤 + 푒1 ‖ + 1푒2 푞 
 (퐾 푊푆 1) {푤(1), (1),푞 2 (26) 
 (1) (1)
 −(퐾( , )푤 + 푒2 ) + 푞 ≥ 푒2, 푞 ≥ 0.
 Hàm Lagrange của bài toán: 
 1 2
 퐿(푤(1), (1), 푞, 훼, 훽) = ‖퐾( , )푤(1) + 푒 (1)‖ + 푒 푞 
 2 1 1 2
 (1) (1)
 −훼 (−(퐾( , )푤 + 푒2 ) + 푞 − 푒2)
− 훽 푞, (27) 
 Dựa vào hệ điều kiện K.K.T của bài toán ta có: 
 퐾( ,  ) (1) 퐾( ,  ) 
 [ ( ) ] 푤
 [ ] 퐾 ,     푒1 [ (1) ] + [ ] 훼 = 0. (28) 
 푒1 푒2
 (1)
 (1) 푤
 Đặt 푆 = [퐾( ,  )   푒1],    푅 = [퐾( ,  )   푒2],    = [ ], 
 (1)
biểu thức (28) có thể được viết lại thành 
 푆 푆 (1) + 푅 훼 = 0,   hay   (1) = −(푆 푆)−1푅 훼. (29) 
 Bài toán đối ngẫu của KTWSVM1 là: 
 1 −1 
 max 푒2 훼 − 훼 푅(푆 푆) 푅 훼
 (퐾 푊푆 1) { 훼 2 (30) 
 0 ≤ 훼 ≤ 1푒2.
 Tương tự ta có bài toán tối ưu KTWSVM2 và KDTWSVM2 cho mặt 
퐾( ,  )푤(2) + (2) = 0 như sau: 
 1 (2) (2) 2 
 min ‖퐾( , )푤 + 푒2 ‖ + 2푒1 푞 
 (퐾 푊푆 2) {푤(2), (2),푞 2 (31) 
 (2) (2)
 (퐾( , )푤 + 푒1 ) + 푞 ≥ 푒1, 푞 ≥ 0.
 1 −1 
 max 푒1 훾 − 훾 푆(푅 푅) 푆 훾
 (퐾 푊푆 2) { 훾 2 (32) 
 0 ≤ 훾 ≤ 2푒1.
 9 
Máy véc-tơ tựa song sinh và áp dụng 
 (2)
 ( ) 푤
 Nghiệm 2 = [ ] = (푅 푅)−1푆 훾. Bằng cách sử dụng công thức Sherman-
 (2)
Morrison-Woodbury [8] cho ma trận nghịch đảo, ta không phải tính nghịch đảo của 
ma trận + 1 chiều như trên mà chỉ phải tính nghịch đảo của ma trận 1 chiều và 2 
chiều. 
6. CÀI ĐẶT THUẬT TOÁN MÁY VÉC-TƠ TỰA SONG SINH VÀ ÁP DỤNG 
 Thuật toán TWSVM: Cho điểm dữ liệu trong 푹풏 được biểu diễn bởi ma trận 
 ×풏
푪 . Giả sử tập dữ liệu gồm hai lớp, lớp {+} gồm điểm và lớp {-} gồm điểm tương ứng 
được biểu diễn bởi các ma trận ×풏 và ×풏. Với K là một kernel nào đó; 
 (1)
 (1) 푤
 i) Đặt 푆 = [퐾( ,  )   푒1],    푅 = [퐾( ,  )   푒2],    = [ ], với 푒1 ∈
 (1)
 1×1 2×1
 푅 , 푒2 ∈ 푅 là các vector toàn 1. 
 ii) Xác định 훼 thông qua (30). 
 iii) Xác định (1) thông qua (29). 
 iv) Phân loại một điểm x mới dựa vào (24). 
 Ngôn ngữ lập trình được sử dụng ở đây là Python 3.8.3. Trong các thư viện của 
Python mới chỉ cài đặt thuật toán SVM mặc dù đã có khá nhiều cải tiến tốt hơn, tiêu 
biểu là thuật toán TWSVM. Tôi đã cài đặt thuật toán TWSVM và đưa phần code lên 
web, bạn đọc quan tâm có thể tìm thấy tại 
https://github.com/makeho8/python/blob/master. Về cơ bản ta cần sử dụng một vài 
thư viện của Python: 
import numpy as np 
from cvxopt import matrix, solvers 
from sklearn.base import BaseEstimator 
K = matrix(GB.dot(np.linalg.inv(HA.T.dot(HA) + 0.0001*I)).dot(GB.T)) 
q = matrix((-e_B)) 
G = matrix(np.vstack((-np.eye(m_B), np.eye(m_B)))) 
h = matrix(np.vstack((np.zeros((m_B,1)), self.c*np.ones((m_B,1))))) 
solvers.options['show_progress'] = False 
sol = solvers.qp(K, q, G, h) 
alpha = np.array(sol['x']) 
self.u = -np.linalg.inv(((HA.T).dot(HA) + 0.0001*I)).dot(GB.T).dot(alpha) 
 10 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ, Trường Đại học Khoa học, ĐH Huế Tập 17, Số 1 (2020) 
self.b_A = self.u[-1] 
 Dưới đây tôi đưa ra kết quả áp dụng thực tế để so sánh giữa TWSVM và SVM 
tiêu chuẩn. Bạn đọc có thể thấy rằng TWSVM là tốt hơn SVM cả về tốc độ tính toán và 
khả năng mô phỏng dữ liệu trong hầu hết các trường hợp. Dữ liệu được lấy từ bộ dữ 
liệu sẵn có UCI [10]. Các hệ số phạt đều được cài đặt là 1. Sử dụng đánh giá chéo 10 lần 
(10-fold cross validation) để đánh giá độ chính xác kiểm thử cho tất cả các tập dữ liệu. 
Tập dữ liệu được chia theo tỉ lệ 80/20, Laptop sử dụng là MSI Bravo15. 
 Bảng 1: Độ chính xác (%) 
 Dữ liệu TWSVM SVM 
 CMC (1473x9) 68.253 +/- 3.065 66.977 +/- 3.921 
 Heart (920x13) 79.902 +/- 5.098 80.170 +/- 4.629 
 Image (2100x18) 84.345 +/- 2.306 76.905 +/- 2.564 
 Hepatitis (155x19) 82.821 +/- 8.107 78.013 +/- 9.178 
 Australian (689x14) 85.107 +/- 4.153 78.750 +/- 7.659 
 BUPA-liver (345x6) 66.283 +/- 7.592 68.016 +/- 10.710 
 Credit (690x16) 86.416 +/- 2.695 85.513 +/- 3.955 
 Diabetis (768x9) 77.205 +/- 4.605 74.923 +/- 5.606 
 Flare-solar (1066x13) 89.793 +/- 2.500 90.379 +/- 2.193 
 German (999x25) 76.475 +/- 4.446 75.228 +/- 5.326 
 Ionosphere (350x35) 89.643 +/- 5.858 86.786 +/- 4.532 
 Spect (265x23) 80.649 +/- 8.113 80.152 +/- 7.070 
 Bảng 2: Tốc độ chạy (ms) 
 Dữ liệu TWSVM SVM 
 CMC (1473x9) 269.06 3619.811 
 Heart (920x13) 78.017 1297.29 
 Image (2100x18) 1029.228 8343.87 
 Hepatitis (155x19) 6 34 
 Australian (689x14) 46.011 905.202 
 BUPA-liver (345x6) 14 161 
 Credit (690x16) 59.015 759.171 
 Diabetis (768x9) 64.014 846.189 
 Flare-solar (1066x13) 136.032 1659.375 
 German (999x25) 148.032 1480.331 
 Ionosphere (350x35) 14.002 167.037 
 Spect (265x23) 12.002 108.023 
 11 
Máy véc-tơ tựa song sinh và áp dụng 
7. KẾT LUẬN 
 Như vậy tư tưởng toán học của máy véc-tơ tựa song sinh thực chất là tìm cách 
tách các lớp dữ liệu bởi hai siêu phẳng không nhất nhiết song song, trong đó mỗi siêu 
phẳng là gần nhất với một lớp và xa nhất có thể với lớp còn lại. Bằng một phương 
pháp nhất quán là sử dụng quy tắc nhân tử Lagrange để giải hai bài toán QP, chúng tôi 
đã trình bày cơ sở toán học của máy véc-tơ tựa song sinh và các nghiên cứu liên quan 
như, SVM tiêu chuẩn, PSVM, GEPSVM trong kĩ thuật phân lớp dữ liệu. Cùng với đó là 
cách cài đặt thuật toán máy véc-tơ tựa song sinh bằng ngôn ngữ lập trình Python, 
nhằm mục đính đánh giá về tốc độ và khả năng mô phỏng dữ liệu của TWSVM so với 
SVM tiêu chuẩn, cho các trường hợp khác nhau, từ đơn giản đến phức tạp. Cánh tiếp 
cận của TWSVM trong trường hợp phi tuyến có thể được giải quyết thông qua bài toán 
quy hoạch nửa xác định dương và quy hoạch nón bậc hai, đây là hướng nghiên cứu 
tiếp theo của chúng tôi nhằm mục đích cải tiến thuật toán. 
 TÀI LIỆU THAM KHẢO 
[1]. B.N Parlett (1998), The symmetric eigenvalue problem. Philadelphia: SIAM. 
[2]. C. Saunders, A. Gammerman, and V. Vovk (1998), Ridge regression learning algorithm in 
 dual variables, Proc. 15th Int’l Conf. Machine learning, pp.515-521. 
[3]. B. Scholkopf and A. Smola (2002), Learning with kernel. Cambridge, Mass.: MIT Press. 
[4]. O. L. Mangasarian and E. W. Wild (2006), “Multisurface proximal support vector 
 classification via generalized eigenvalues,” IEEE Trans. Pattern analysis and machine learning, 
 vol. 28, no. 1, pp. 69-74. 
[5]. Jayadeva, R. Khemchandani and S. Chandra (2007), Twin support vector machines for 
 pattern classification. IEEE Transactions on Pattern Analysis and Machine intelligence, vol. 29, 
 no. 5. 
[6]. G. Fung and O. L Mangasarian (2001), “Proximal support vector machine,” Proc. Seventh 
 Int’l Conf. Knowledge discovery and Data mining, pp. 77-86. 
[7]. O. L. Mangasarian (1994), Nonlinear programming. SIAM, Philadelphia, PA. 
[8]. G. H. Golub and C. F. Van Loan (1996), Matrix computations. The John Hopkins University 
 Press, Baltimore, Maryland, 3rd edition. 
[9]. A.N. Tikhonov and V. Y. Arsen (1977), Solutions of Ill-Posed Problems. New York: John 
 Wiley and Sons. 
[10]. C. L. and C.J. Merz (1998), “UCI Repository for Machine Learning Database,” Dept. of 
 information and computer sciences, Univ. of California, Irvine, 
 12 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ, Trường Đại học Khoa học, ĐH Huế Tập 17, Số 1 (2020) 
 TWIN SUPPORT VECTOR MACHINE AND APPLICATION 
 Nguyen The Cuong 
 Department of Mathematics, Communications University Nha Trang, Khanh Hoa 
 Email: nckcbnckcb@gmail.com 
 ABSTRACT 
 The support vector machines are popular classification technique and has been 
 successfully applied to many different areas of the life. Because this is a pratical 
 problem, we chose to study, aiming to find more applications and better 
 improvings. There are some typical improvings such as Proximal Support Vector 
 Machine (PSVM), Proximal Support Vector Machine Via Generalized Eigenvalues 
 (GEPSVM) and Twin Support Vector Machine (TWSVM). SVM and TWSVM can 
 be solved by using Lagrange duality problem, but TWSVM used two nonparallel 
 hyperplanes to separate data classes. This paper airms to show mathematical 
 foundation of PSVM, GEPSVM and TWSVM, and we have setted up TWSVM 
 algorithm by using Python programming to evaluate effect of TWSVM compared 
 to standard SVM. 
 Keywords: Support vector machines, Twin support vector machines. 
 Nguyễn Thế Cường sinh ngày 09/12/1986 tại Sơn La. Năm 2009, ông tốt 
 nghiệp cử nhân ngành Toán Tin tại Trường Đại học Sư phạm Hà Nội. 
 Năm 2014, ông tốt nghiệp thạc sỹ ngành Toán Giải tích tại Trường Đại học 
 khoa học, ĐH Huế. Tháng 12/2018, ông bắt đầu làm NCS tại Trường Đại 
 học Khoa học, ĐH Huế. Hiện ông đang công tác tại Trường ĐH Thông tin 
 Liên lạc, Nha Trang, Khánh Hòa. 
 Lĩnh vực nghiên cứu: Khoa học máy tính. 
 13 
Máy véc-tơ tựa song sinh và áp dụng 
 14