Mạng vô tuyến chuyển tiếp không đồng bộ với hồi tiếp pha

á
trị lớn nhất và được trình bày trong mục 3.
Trên thực tế, khoảng cách từ các nút chuyển tiếp đến nút đích là lớn hơn rất nhiều
so với khoảng cách giữa hai ăng-ten trên cùng một nút chuyển tiếp, do vậy có thể xem
tín hiệu nhận được tại nút đích từ các ăng-ten của cùng một nút chuyển tiếp có thời
gian trễ như nhau do có cùng khoảng cách. Trong khi đó do sự phân tán tự nhiên của
các nút chuyển tiếp, tín hiệu thu được từ các nút chuyển tiếp khác nhau lại có thời gian
trễ khác nhau do khoảng cách thực tế từ các nút chuyển tiếp tới nút đích là khác nhau.
Ký hiệu τik là thời gian trễ từ ăng-ten antik tới nút đích, không làm mất tính tổng quát
ta có thể giả sử rằng τ11 = τ12 = 0 và τ21 = τ22 = τ 6= 0. Theo đó, tín hiệu thu tại nút
đích có thể viết dưới dạng:
r(n) =
√
P2
[
g11 g21 g12 g22
]
sR(n)+Iint(n)+z(n),
=
√
P2hs(n)+Iint(n)+z(n), (3)
trong đó h = g11 + b1g21 + b2g12 + b3g22 là tăng ích kênh tương đương, z(n) là tạp âm
tại nút đích, và Iint(n) là thành phần nhiễu ISI:
Iint(n) =
√
P2 {b2g12(−1) + b3g22(−1)} s(n− 1). (4)
Các hệ số gi2(−1), (i = 1, 2) trong (4) biểu diễn các tăng ích kênh giữa các ăng-ten
của nút chuyển tiếp thứ hai và nút đích do ảnh hưởng bởi hiện tượng không đồng bộ.
Độ lớn của gi2(−1) có thể biểu diễn dưới dạng tỉ số như sau [1]:
β = |gi2(−1)|2/|gi2|2; i = 1, 2 (5)
với β = 0 khi τ = 0 và β = 1 khi τ = 0.5T . Lưu ý rằng, các hệ số tăng ích
gi2(l), l = −2,−3... được bỏ qua vì có độ lớn không đáng kể. Hệ số
√
P2/2 trong
81
Chuyên san Công nghệ thông tin và Truyền thông - Số 10 (06-2017)
phương trình (3) để đảm bảo công suất phát tại mỗi nút chuyển tiếp là P2. Rõ ràng,
trong tín hiệu thu (3) chỉ tồn tại một thành phần ISI và là loại P-ISI, và có thể được
mô tả trực quan trên Hình 3. Chỉ bằng so sánh Hình 1 và Hình 3, chúng ta cũng có
thể thấy rằng sơ đồ hồi tiếp pha có số thành phần ISI ít hơn so với các sơ đồ DCL
QO-STBC và DCL EO-STBC trước đây. Hơn nữa, đây lại là loại P-ISI nên sẽ có thể
loại bỏ được một cách hoàn toàn với bộ giải mã NOD và sẽ được trình bày trong mục 3
tiếp theo.
3. Lựa chọn bít hồi tiếp và giải mã NOD
3.1. Lựa chọn bít hồi tiếp
Từ phương trình biểu diễn tín hiệu thu (3), tỉ số SNR thu tại nút đích được xác định
như sau
γ =
P2λ
δ2z
, (6)
trong đó λ = h∗h = α + χ là tăng ích phẩm chất tổng thể của hệ thống, với (•)∗ kí
hiệu phép lấy liên hợp phức. Tăng ích tổng thể của sơ đồ đề xuất bao gồm hai thành
phần là tăng ích phân tập thông thường α và tăng ích mảng χ, và được xác định như
sau
α = |g11|2 + |g21|2 + |g12|2 + |g22|2; (7)
χ =2b1< (g11g∗21) + 2b2< (g11g∗12 + b1g21g∗12)
+ 2b3< (g11g∗22 + b1g21g∗22 + b2g12g∗22) , (8)
trong đó <(•) kí hiệu phép lấy phần thực của số phức. Trước khi truyền dữ liệu, nút
đích căn cứ vào thông tin trạng thái kênh (CSI: Channel State Information) có được từ
các nút chuyển tiếp đến nó thông qua huấn luyện kênh hay symbol hoa tiêu tính toán
để xác định giá trị pha hồi tiếp và gửi về các nút chuyển tiếp qua kênh hồi tiếp. Tiêu
chuẩn lựa chọn pha hồi tiếp để đạt được SNR lớn nhất được cho như sau:
(θ1, θ2, θ3) = argmax
θ1,θ2,θ3∈(0,pi)
γ = argmax
θ1,θ2,θ3∈(0,pi)
χ. (9)
Khi dung lượng kênh hồi tiếp không bị hạn chế thì nút đích có thể gửi đầy đủ giá
trị của pha hồi tiếp θ1, θ2, θ3 trong (9) về nút chuyển tiếp và chất lượng hệ thống nhận
được chắc chắn sẽ là tốt nhất. Tuy nhiên, trên thực tế kênh hồi tiếp thường chỉ được
phân bổ một dung lượng nhỏ, vì vậy, thông tin hồi tiếp cần được lượng tử hóa để phù
hợp với dung lượng giới hạn của kênh hồi tiếp. Trong trường hợp này chúng tôi đề xuất
giá trị pha hồi tiếp chỉ nhận một trong hai giá trị là 0 hoặc pi, tức θi = {0, pi} tương
ứng với bi = {1,−1} và chỉ cần một bít hồi tiếp cho mỗi giá trị pha hồi tiếp θi. Khi
này, thuật toán lựa chọn pha hồi tiếp để đạt được SNR lớn nhất trong (9) tương đương
82
Tạp chí Khoa học và Kỹ thuật - Học viện KTQS - Số 184 (06-2017)
với thuật toán xác định các bít hồi tiếp để giá trị tăng ích mảng χ trong (8) đạt giá trị
lớn nhất:
b1, b2, b3 = arg max
b1,b2,b3∈{−1,1}
χ. (10)
Thuật toán vét cạn tìm kiếm toàn bộ các khả năng trong (10) cho phép hệ thống
nhận được tăng ích mảng lớn nhất. Tuy nhiên số lượng phép toán cần thực hiện lớn,
do đó chúng tôi đề xuất một thuật toán qui nạp gồm ba bước đơn giản hơn để thay thế
như sau:
Bước 1: b1 =
{
1 nếu < (g11g∗21) ≥ 0
−1 nếu < (g11g∗21) < 0
Bước 2: b2 =
{
1 nếu < (g11g∗12 + b1g21g∗12) ≥ 0
−1 nếu < (g11g∗12 + b1g21g∗12) < 0
Bước 3: b3 =
{
1 nếu < (g11g∗22 + b1g21g∗22 +b2g12g∗22) ≥ 0
−1 nếu < (g11g∗22 + b1g21g∗22 +b2g12g∗22) < 0
So sánh tỉ số SNR của sơ đồ đề xuất trong phương trình (6) và phương trình (18)
trong công trình [1] có thể thấy, tăng ích phân tập của hai sơ đồ như nhau, trong khi
tăng ích mảng của sơ đồ đề xuất có giá trị lớn hơn. Nói cách khác, sơ đồ đề xuất đạt
được sự cải thiện phẩm chất xét trên khía cạnh SNR thu.
3.2. Giải mã NOD
Giải mã NOD được đề xuất cho sơ đồ DCL EO-STBC [1] và hoàn toàn có thể được
áp dụng cho sơ đồ pha hồi tiếp để nút đích giải mã tín hiệu phát s (n) từ tín hiệu
thu r (n) trong (3). Trong thực tế, tín hiệu s(n − 1) có thể biết được trước khi thực
hiện tách sóng nếu quá trình giải mã được bắt đầu một cách hợp lý (ví dụ thông qua
sử dụng symbol hoa tiêu tại đầu của mỗi khung truyền dẫn) hoặc có thể sử dụng tín
hiệu tách sóng sˆ(n − 1) của chu kỳ trước đó. Do đó, thành phần nhiễu liên ký hiệu
Iint(n) =
√
P2 {b2g12(−1) + b3g22(−1)} sˆ(n− 1) trong công thức (3) có thể khôi phục
được trước khi thực hiện quá trình giải mã. Thuật toán giải mã NOD cho sơ đồ hồi tiếp
pha được thực hiện thông qua hai bước như sau:
Bước 1: Loại bỏ nhiễu P-ISI Iint(n) trong tín hiệu thu (3):
r′(n) = r(n)−
√
P2 {b2g12(−1) + b3g22(−1)} sˆ(n− 1) (11)
trong đó sˆ (n− 1) là tín hiệu giải mã của chu kỳ trước đó.
Bước 2: Quyết định tín hiệu được giải mã. Do giả thiết nút đích có được đầy đủ CSI
từ các nút chuyển tiếp đến nó, giải mã tín hiệu thu tại nút đích được thực hiện như sau:
s˜(n) = argmin
sm∈A
∣∣∣r′(n)−√P2hsm∣∣∣2, (12)
trong đó A kí hiệu chòm sao tín hiệu điều chế.
83
Chuyên san Công nghệ thông tin và Truyền thông - Số 10 (06-2017)
Từ phương trình (11) có thể thấy, nếu việc giải mã của chu kỳ trước là không có lỗi
tức sˆ (n− 1) = s (n− 1) thì thành phần nhiễu Iint(n) trong tín hiệu thu (3) được loại
bỏ hoàn toàn và tách sóng (12) là tách sóng tối ưu, tuy nhiên trên thực tế vẫn có lỗi
xảy ra trong quá trình giải mã tại nút đích tức sˆ (n− 1) 6= s (n− 1) nên quá trình giải
mã trong (12) là giải mã cận tối ưu.
4. Các kết quả mô phỏng và so sánh
Mục này trình bày các kết quả mô phỏng Monte-Carlo tỉ số bít lỗi (BER: Bit Error
Rate) như là một hàm số của tổng công suất phát toàn mạng P (dB) để đánh giá chất
lượng của sơ đồ hồi tiếp pha được đề xuất trong mục 2 với điều chế khóa dịch pha
(QPSK: Quadrature Phase Shift Keying). Giả thiết các bít hồi tiếp coi như được truyền
từ nút đích về các nút chuyển tiếp qua một kênh hồi tiếp tiếp lý tưởng không lỗi, không
trễ và đồng bộ.
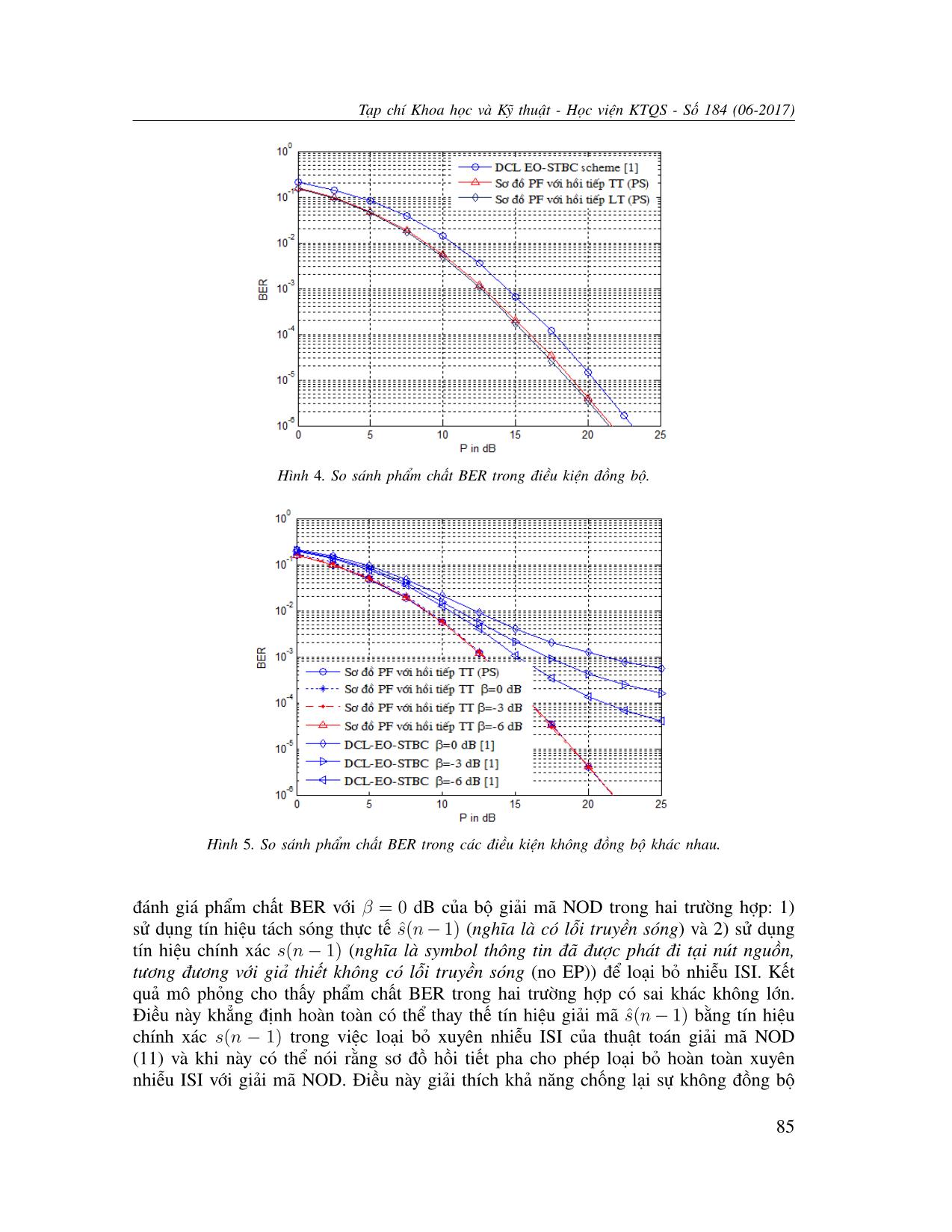
Hình 4 trình bày so sánh kết quả mô phỏng BER của sơ đồ hồi tiếp pha khi dung
lượng kênh hồi tiếp là vô hạn (kênh LT: lý tưởng), tức nút chuyển tiếp có thể biết được
đầy đủ thông tin pha θ1, θ2, θ3 và dung lượng kênh hồi tiếp là hữu hạn (kênh TT: thực
tế), tức nút chuyển tiếp chỉ biết được các giá trị b1, b2, b3 để so sánh với sơ đồ DCL
EO-STBC [1] trong điều kiện đồng bộ, tức β = 0. Từ Hình 4 có thể thấy rằng độ dốc
hai đường cong BER của hai sơ đồ là như nhau, có nghĩa hai sơ đồ nhận được cùng
tăng ích phân tập. Tuy nhiên, sơ đồ hồi tiếp pha nhận được độ lợi SNR xấp xỉ 2,3 dB
so với sơ đồ DCL EO-STBC, do nó có tăng ích mảng χ lớn hơn. So sánh phẩm chất
BER của sơ đồ đề xuất khi sử dụng kênh hồi tiếp LT hoặc khi sử dụng kênh hồi tiếp
TT cho thấy chất lượng hệ thống khi dung lượng kênh hồi tiếp hữu hạn có giảm một
chút so với kênh hồi tiếp vô hạn (cỡ 0,5 dB tại BER = 10−4) là cái giá chấp nhận
được cho việc giảm số bít hồi tiếp từ vô hạn xuống còn 3 bít hồi tiếp.
Hình 5 trình bày kết quả mô phỏng cho trường hợp không đồng bộ với các mức
không đồng bộ khác nhau, nghĩa là, với các giá trị β khác nhau. Từ các kết quả mô
phỏng trên Hình 5 cho thấy: i) sơ đồ hồi tiếp pha có thể chống lại sự không đồng bộ
một cách hiệu quả thể hiện bởi các đường cong BER cho các giá trị β = −6 dB; −3
dB; 0 dB gần như trùng với đường cong BER trong điều kiện đồng bộ, tức β = 0; ii)
sơ đồ hồi tiếp pha nhận được độ lợi SNR đáng kể so với sơ đồ DCL EO-STBC [1], ví
dụ tại BER = 10−3 độ lợi SNR của sơ đồ hồi tiếp pha cho các mức không đồng bộ
β = −6 dB; −3 dB; 0 dB tương ứng là 2,5 dB, 5,0 dB và 8,2 dB so với sơ đồ DCL
EO-STBC [1]; iii) phẩm chất BER của sơ đồ đề xuất hầu như không phụ thuộc vào
mức độ không đồng bộ (phản ánh qua tham số β), nguyên nhân là do nhiễu ISI trong
tín hiệu thu tại nút đích đã được loại bỏ một cách hoàn toàn trước khi thực hiện tách
sóng.
Như đã phân tích trong mục 3.2, phẩm chất bộ giải mã NOD phụ thuộc vào tín hiệu
khởi đầu sˆ(n− 1) được sử dụng để loại bỏ thành phần nhiễu ISI trước khi tách sóng.
Thực tế, tín hiệu sau tách sóng sˆ(n − 1) hoàn toàn có thể khác tín hiệu được phát đi
s(n−1) do lỗi truyền sóng (EP: Error Propagation). Hình 6 trình bày kết quả mô phỏng
84
Tạp chí Khoa học và Kỹ thuật - Học viện KTQS - Số 184 (06-2017)
Hình 4. So sánh phẩm chất BER trong điều kiện đồng bộ.
Hình 5. So sánh phẩm chất BER trong các điều kiện không đồng bộ khác nhau.
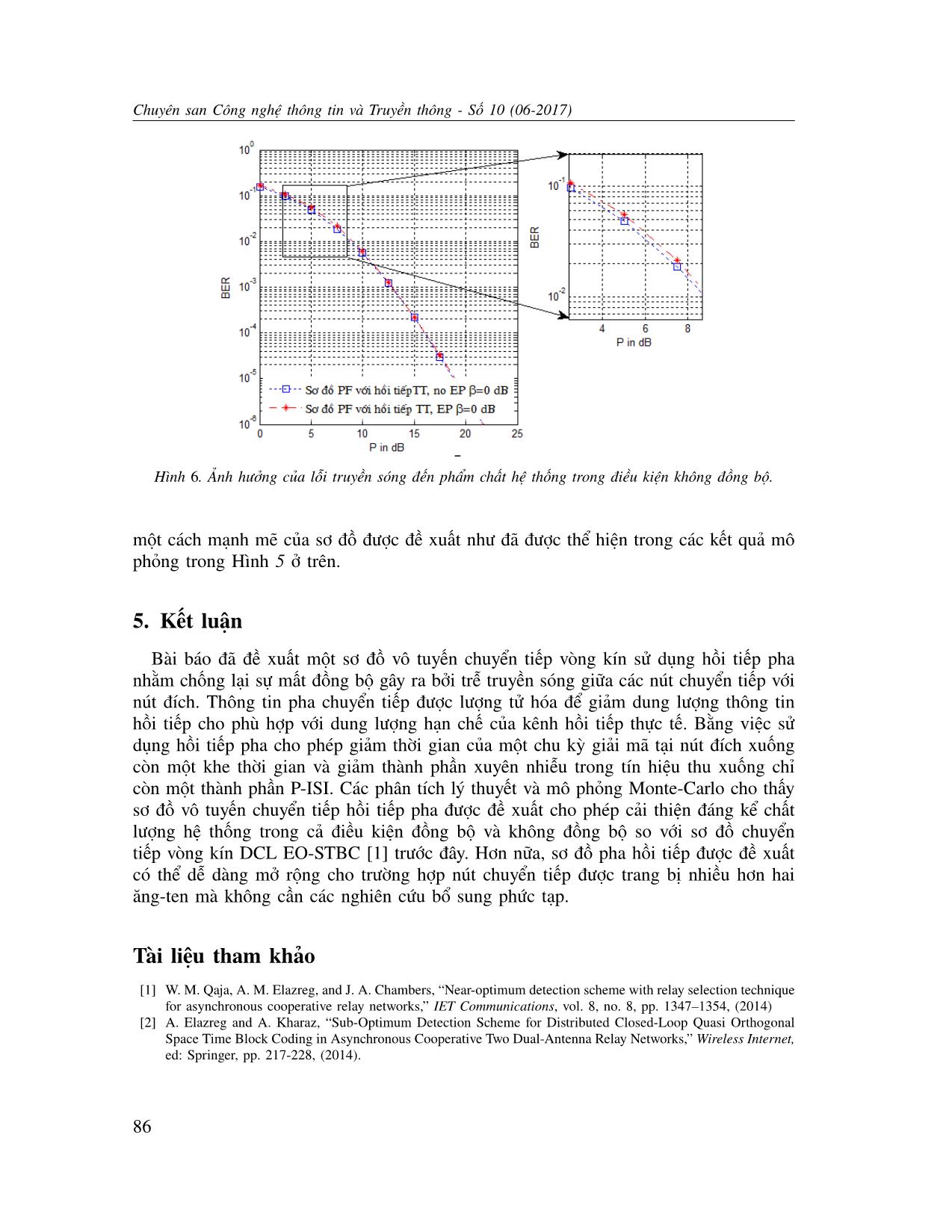
đánh giá phẩm chất BER với β = 0 dB của bộ giải mã NOD trong hai trường hợp: 1)
sử dụng tín hiệu tách sóng thực tế sˆ(n− 1) (nghĩa là có lỗi truyền sóng) và 2) sử dụng
tín hiệu chính xác s(n− 1) (nghĩa là symbol thông tin đã được phát đi tại nút nguồn,
tương đương với giả thiết không có lỗi truyền sóng (no EP)) để loại bỏ nhiễu ISI. Kết
quả mô phỏng cho thấy phẩm chất BER trong hai trường hợp có sai khác không lớn.
Điều này khẳng định hoàn toàn có thể thay thế tín hiệu giải mã sˆ(n− 1) bằng tín hiệu
chính xác s(n − 1) trong việc loại bỏ xuyên nhiễu ISI của thuật toán giải mã NOD
(11) và khi này có thể nói rằng sơ đồ hồi tiết pha cho phép loại bỏ hoàn toàn xuyên
nhiễu ISI với giải mã NOD. Điều này giải thích khả năng chống lại sự không đồng bộ
85
Chuyên san Công nghệ thông tin và Truyền thông - Số 10 (06-2017)
Hình 6. Ảnh hưởng của lỗi truyền sóng đến phẩm chất hệ thống trong điều kiện không đồng bộ.
một cách mạnh mẽ của sơ đồ được đề xuất như đã được thể hiện trong các kết quả mô
phỏng trong Hình 5 ở trên.
5. Kết luận
Bài báo đã đề xuất một sơ đồ vô tuyến chuyển tiếp vòng kín sử dụng hồi tiếp pha
nhằm chống lại sự mất đồng bộ gây ra bởi trễ truyền sóng giữa các nút chuyển tiếp với
nút đích. Thông tin pha chuyển tiếp được lượng tử hóa để giảm dung lượng thông tin
hồi tiếp cho phù hợp với dung lượng hạn chế của kênh hồi tiếp thực tế. Bằng việc sử
dụng hồi tiếp pha cho phép giảm thời gian của một chu kỳ giải mã tại nút đích xuống
còn một khe thời gian và giảm thành phần xuyên nhiễu trong tín hiệu thu xuống chỉ
còn một thành phần P-ISI. Các phân tích lý thuyết và mô phỏng Monte-Carlo cho thấy
sơ đồ vô tuyến chuyển tiếp hồi tiếp pha được đề xuất cho phép cải thiện đáng kể chất
lượng hệ thống trong cả điều kiện đồng bộ và không đồng bộ so với sơ đồ chuyển
tiếp vòng kín DCL EO-STBC [1] trước đây. Hơn nữa, sơ đồ pha hồi tiếp được đề xuất
có thể dễ dàng mở rộng cho trường hợp nút chuyển tiếp được trang bị nhiều hơn hai
ăng-ten mà không cần các nghiên cứu bổ sung phức tạp.
Tài liệu tham khảo
[1] W. M. Qaja, A. M. Elazreg, and J. A. Chambers, “Near-optimum detection scheme with relay selection technique
for asynchronous cooperative relay networks,” IET Communications, vol. 8, no. 8, pp. 1347–1354, (2014)
[2] A. Elazreg and A. Kharaz, “Sub-Optimum Detection Scheme for Distributed Closed-Loop Quasi Orthogonal
Space Time Block Coding in Asynchronous Cooperative Two Dual-Antenna Relay Networks,” Wireless Internet,
ed: Springer, pp. 217-228, (2014).
86
Tạp chí Khoa học và Kỹ thuật - Học viện KTQS - Số 184 (06-2017)
[3] M. T. O. E. Astal and J. C. Olivier, “Distributed Closed-Loop Extended Orthogonal STBC: Improved
performance in imperfect synchronization,” in: Proc. Personal Indoor and Mobile Radio Commun., England,
pp. 1941-1945, (2013).
[4] A. M. Elazreg, F. M. Abdurahman, and J. A. Chambers, “Distributed closed-loop quasi-orthogonal space time
block coding with four relay nodes: overcoming imperfect synchronization,” in: Proc. IEEE Int. Conf. on
Wireless and Mobile Computing, Netw. and Commun., WIMOB, pp. 320-325, (2009).
[5] Desouky, Ahmed, and Ahmed El-Mahdy, “Asynchronous down-link cooperative communication scheme in
Rayleigh fading wireless environment,” in: Proc. Signal Processing: Algorithms, Architectures, Arrangements,
and Applications, pp.142-146, (2016)
[6] A. Elazreg and J. Chambers, “Closed-loop extended orthogonal space time block coding for four relay nodes
under imperfect synchronization,” in: Proc. Workshop on Statistical Signal Processing, pp. 545-548, (2009).
[7] F.-C. Zheng, A. G. Burr, and S. Olafsson, “Signal Detection for Distributed Space-Time Block Coding: 4 Relay
Nodes under Quasi-Synchronisation,” IEEE Transactions on Communications, vol. 57, no. 5, pp. 1250-1255,
(2009).
[8] A. M. Elazreg and J. A. Chambers, “Sub-optimum detection scheme for asynchronous cooperative relay
networks,” IET Communications, vol. 5, no. 15, pp. 2250-2255, (2011).
[9] L. Guangxiang and W. Zhuo, “Signal detection for cooperative cellular systems with 4 relay nodes under
imperfect synchronization,” in: Proc. Signal Processing, Commun. and Computing, pp. 1-6, (2013).
[10] F. C. Zheng, A. G. Burr, and S. Olafsson, “Near-optimum detection for distributed space-time block coding
under imperfect synchronization,” IEEE Transactions on Communications, vol. 56, no. 11, pp. 1795-1799,
(2008).
[11] M.-T. E. Astal, A. M. Abu-Hudrouss, and J. C. Olivier, “Improved signal detection of wireless relaying networks
employing space-time block codes under imperfect synchronization,” Wireless Personal Communications, vol.
82, no. 1, pp. 533-550, (2015).
[12] G. Celik and H. Celebi, “G-CRLB analysis of time delay based localization for decode-and-forward cooperative
relay networks in multipath environments,” in: Proc. Int. Wireless Commun. and Mobile Computing, pp. 454-
459, (2015).
[13] Y. Jing, “Combination of MRC and distributed space-time coding in networks with multiple-antenna relays,”
IEEE Trans. on Wireless Commun., vol. 9, pp. 2550-2559, (2010).
Ngày nhận bài 21-4-2017; Ngày chấp nhận đăng 23-8-2017.

Trần Thế Nghiệp nhận bằng kỹ sư ngành điện, điện tử năm 2006 tại Học viện Kỹ thuật Quân
sự và thạc sĩ ngành kỹ thuật điện tử tại Học viện Công nghệ Bưu chính Viễn thông năm 2011.
Hiện tại đang làm nghiên cứu sinh tại Học viện Kỹ thuật Quân sự. Hướng nghiên cứu hiện
tại là: mã không gian-thời gian, mã không gian-thời gian phân tán và truyền thông hợp tác
MIMO.
87