Lược đồ sai phân khác thường mô phỏng số mô hình siêu quần thể: Sử dụng định lý ổn định Lyapunov

 (1). So với cách chứng minh của chúng tôi trước đây, cách chứng minh sử dụng sử dụng định lý ổn định 
Lyapunov ngắn gọn và đơn giản hơn rất nhiều. Ở đây, không cần thực hiện các tính toán phức tạp và các kỹ thuật tinh 
vi. Cách tiếp cận này có thể được áp dụng cho các lớp bài toán tương tự. 
 Trong phần II lược đồ sai phân khác thường bảo toàn các tính chất của mô hình (1) được xây dựng. Phần III 
trình bày các thử nghiệm số nhằm chỉ ra các kết quả lý thuyết là hoàn toàn đúng đắn. Phần kết luận và hướng nghiên 
cứu tiếp theo được trình bày trong phần IV. 
II. XÂY DỰNG LƯỢC ĐỒ SAI PHÂN KHÁC THƯỜNG 
Chúng tôi đề xuất lược đồ sai phân khác thường cho mô hình (1) ở dạng 
 ( , ( 
 ( ( 
 khi . 
So với lược đồ chúng tôi đã xây dựng trước đây [1] lược đồ (3) đơn giản hơn, chỉ chứa một tham số . Mục 
tiêu của chúng ta là xác định điều kiện đặt lên hàm mẫu số đề lược đồ (3) bảo toàn các tính chất ( ( của mô 
hình (1). 
A. Tính chất hội tụ đơn điệu của tổng ( ( ( 
Định lý 1. Lược đồ sai phân (3) bảo toàn tính chất ( của mô hình (1) với mọi hàm ( thỏa mãn. 
 ( ( ( khi . ( 
Chứng minh. Đặt . Cộng vế với vế hai phương trình của (3) ta thu được phương trình sai phân tuyến 
tính với hệ số hằng số đối với 
 ( 
 ( 
 ( 
Dễ dàng tìm được biểu thức nghiệm tường minh của (5) 
 ( 
) (
 ( 
)
 ( 
Chú ý rằng nếu φ là hàm dương thì 
 ( 
 ( Vì thế điểm cân bằng 
 là điểm cân bằng 
ổn định tiệm cận địa phương của phương trình sai phân tuyến tính (5). Do đó nó cũng chính là điểm cân bằng ổn định 
tiệm cận toàn cục. Kết hợp với (6) Định lý được chứng minh. 
B. Tính chất bị chặn 
Định lý 2. Lược đồ sai phân (3) bảo toàn tính chất ( của mô hình (1) nếu hàm ( thỏa mãn điều kiện 
 ( { 
 } ( 
Chứng minh. Ta sẽ chứng minh định lý bằng phương pháp quy nạp toán học. Đầu tiên theo Định lý 1 thì lược đồ (3) 
bảo toàn tính chất ( ( . Do đó, với mọi giá trị ban đầu thỏa mãn (2) thì nghiệm của (1) đều thỏa mãn 
Do đó để chỉ ra lược đồ (3) bảo toàn tính chất ( của mô hình (1) ta chỉ cần chứng minh với mọi giá trị ban 
đầu thỏa mãn (2) thì nghiệm của (3) đều không âm. Thật vậy, dễ dàng đưa lược đồ (3) về dạng lược đồ hiển dạng 
( 
 ( 
Đặng Quang Á, Hoàng Mạnh Tuấn 277 
 ( 
( 
Do hàm thỏa mãn (7) nên từ (8) ta thu được với mọi . Ta cần chỉ ra với mọi 
 và thỏa mãn (2). Thế vào biểu thức của ta nhận được 
 ( 
 ( 
Mẫu số của biểu thức là ( nên ta chỉ cần chỉ ra tử số là không âm. Đặt 
 ( 
thì 
 ( 
 ( 
Do nên 
 ( 
 Mặt khác, do ta có 
 Do đó 
 = 
 ( 
Vì thế từ (10) ta thu được với mọi và thỏa mãn (2). Từ đó Định lý được chứng minh. 
C. Tính chất ổn định toàn cục của tập hợp điểm cân bằng 
Bằng cách sử dụng một định lý mở rộng của Định lý ổn định Lyapunov [9, Theorem 3.3] chúng ta chỉ ra tính 
chất ổn định toàn cục của tập hợp điểm cân bằng. 
1. Trường hợp 
Trường hợp này trên tập {( } } mô hình (1) chỉ có duy nhất điểm cân 
bằng (
 . Chúng ta cần xác định điều kiện đặt lên hàm φ sao điểm cân bằng là ổn định tiệm cận toàn cục 
của phương trình (3), tức là là ổn định tiệm cận địa phương và điểm hút toàn cục. 
Định lý 3. Nếu hàm thỏa mãn các điều kiện của Định lý 2 thì điểm cân bằng là ổn định tiệm cận toàn 
cục của phương trình (3) trên tập D. 
Chứng minh. Sử dụng một mở rộng của Định lý ổn định Lyapunov [9, Theorem 3.3] ta sẽ chỉ ra tính chất ổn 
định toàn cục của . 
Xét hàm ( ( 
)
 trên tập . Ta chỉ ra hàm ( thỏa mãn 4 điều kiện trong Định lý [9, 
Theorem 3.3] trên miền (thay vì trên vì ta chỉ xét tính chất ổn định toàn cục trên ). Rõ ràng hàm ( là liên 
tục trên . Hơn nữa 
1) ( với mọi ( và ( 
2) Ta có 
 ( ( ( ( 
) ( 
) 
 ( ( 
) 
( 
Ta để ý rằng: Do tính chất ( của mô hình được bảo toàn nên với mọi giá trị ban đầu thuộc và ( 
 ( 
 thì 
278 LƯỢC ĐỒ SAI PHÂN KHÁC THƯỜNG MÔ PHỎNG SỐ MÔ HÌNH SIÊU QUẦN THỂ: SỬ DỤNG ĐỊNH LÝ ỔN ĐỊNH LYAPUNOV 
 ( 
Tương tự, với mọi giá trị ban đầu thuộc và ( ( 
 thì 
 ( 
Vì thế từ (11), (12), (13) ta nhận được ( với mọi ( . Do đó, điều kiện (2) của Định lý 
được thỏa mãn. 
3) Mặt khác, từ (11) ta thấy rằng ( khi và chỉ khi ( {( } 
} . Do tính chất ( 
được bảo toàn nên trong trường hợp này ta có = {( } 
} . Ta cần chỉ ra là 
 -ổn định toàn 
cục, tức là là ổn định địa phương trên 
 và với mọi giá trị ban đầu thuộc thì ( ) khi . 
Thật vậy: 
Nếu các giá trị ban đầu thuộc tập , tức là thỏa mãn 
 thì từ (6) ta thấy nghiệm của (3) thỏa 
mãn 
 với mọi , hay tương đương với 
 . Thế vào (5) ta thu được 
( (
( 
) 
 (
) 
( 
Do thỏa mãn các điều kiện của Định lý 2 nên 
 do đó 
 . Mặt khác do nên 
 . Do đó, từ (14) suy ra khi , tức là là điểm hút toàn cục. Bên cạnh đó, từ (14) 
ta thấy 
( 
 ( ( 
Do đó là ổn định tiệm cận địa phương. Kết hợp với là hút toàn cục nên nó là ổn định toàn cục. 
Mặt khác do tính chất ( được bảo toàn nên rõ ràng là là 
 -ổn định toàn cục. Từ đó điều kiện (3) của Định lý 
được thỏa mãn. 
4) Do tính chất ( được bảo toàn nên hiển nhiên mọi nghiệm của (3) đều bị chặn trên . 
Như vậy, các điều kiện của định lý mở rộng của Định lý ổn định Lyapunov được thỏa mãn nên là ổn định toàn cục 
trên . Từ đó định lý được chứng minh. 
2. Trường hợp 
Ta để ý rằng nếu xuất phát từ giá trị ban đầu thì từ (5) ta nhận được nghiệm của (3) là 
 ( 
Do đó dễ dàng chỉ ra trong trường hợp này ( và là ổn định tiệm cận toàn cục. Vì thế trong 
trường hợp ta chỉ xét giá trị ban đầu thuộc vào tập 
 {( } }. Nếu 
 thì là điểm cân bằng duy nhất thuộc vào 
 . Ta cần chỉ ra tính chất ổn định tiệm cận toàn cục trong của 
Định lý sau đây được phát biểu và chứng minh tương tự Định lý 3. 
Định lý 4. Nếu hàm thỏa mãn các điều kiện của Định lý 2 thì điểm cân bằng là ổn định tiệm cận toàn 
cục của phương trình (3) trên tập . 
Chú ý 1. Hàm ( được xây dựng trong chứng minh Định lý 3 không thỏa mãn các điều kiện của Định lý 
ổn định toàn cục Lyapunov cổ điển trên tập {( } 
}. Vì thế ở đây thay vì sử dụng Định lý ổn định 
Lyapunov cổ điển chúng ta sử dụng một mở rộng của Định lý ổn định Lyapunov cổ điển. 
Đặng Quang Á, Hoàng Mạnh Tuấn 279 
Chú ý 2. Mấu chốt quan trọng trong chứng minh tính chất ổn định tiệm cận toàn cục của hai điểm cân bằng 
 và là xây dựng được hàm Lyapunov (mở rộng). Trong trường hợp này, tính chất ( và ( có vai trò đặc biệt 
quan trọng trong việc xây dựng hàm Lyapunov. Nói cách khác thì tính chất ổn định toàn cục của lược đồ sai phân có 
liên kết chặt chẽ với tính chất ( và ( của mô hình. Nếu không có hai tính chất này thì việc chỉ ra hàm Lyapunov 
là cực kỳ khó khăn và phức tạp. 
Chú ý 3. Có thể áp dụng các kỹ thuật trong phần này cho các lược đồ sai phân mà chúng tôi đã đề xuất trước 
đó [1] để chứng minh tính chất ổn định toàn cục của tập hợp điểm cân bằng. 
D. Tính chất không tuần hoàn của nghiệm 
Nhờ tiêu chuẩn Dulax ta dễ dàng chỉ ra mô hình (1) không có nghiệm tuần hoàn. Đối với các phương trình sai 
phân việc chỉ ra tính chất không tuần hoàn của nghiệm phức tạp hơn rất nhiều. Tuy nhiên, do điểm cân bằng là ổn định 
toàn cục nên rõ ràng lược đồ sai phân (3) cũng không thể có nghiệm tuần hoàn. 
Tổng hợp các kết quả ta nhận được các lược đồ bảo toàn chính xác các tính chất cho mô hình (1). 
Định lý 5. Lược đồ sai phân (3) bảo toàn tính chất ( ( của mô hình (1) nếu hàm ( thỏa mãn 
điều kiện 
 ( { 
 } ( 
Chú ý 4. Có rất nhiều cách để lựa chọn hàm thỏa mãn điều kiện (16), chẳng hạn ta có thể chọn hàm 
 ( 
, 
. 
III. CÁC THỬ NGHIỆM SỐ 
Trong phần này chúng tôi trình bày một vài thử nghiệm số nhằm chỉ ra rằng các kết quả lý thuyết nhận được 
bên trên là hoàn toàn chính xác. 
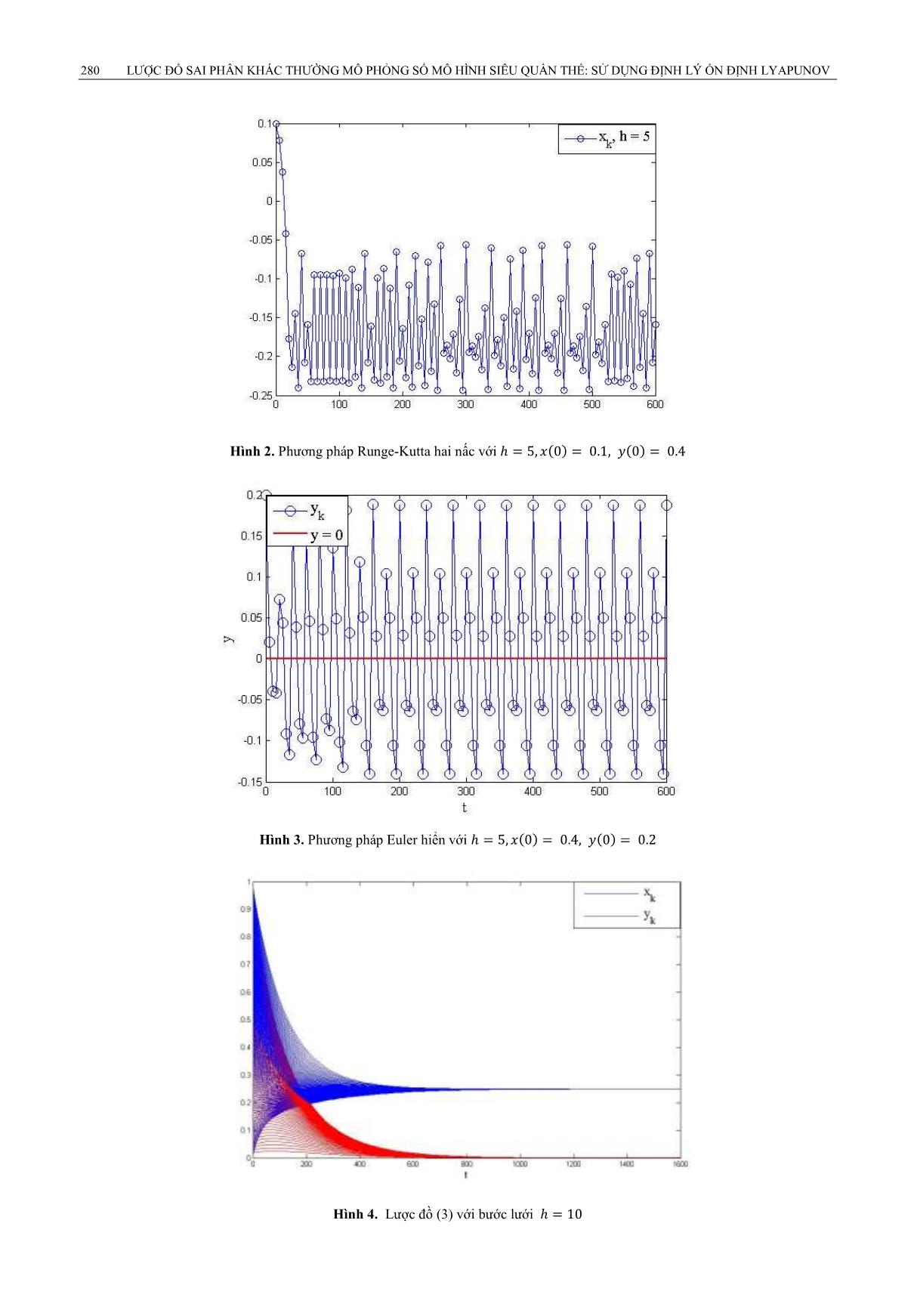
A. Trường hợp 
Xét mô hình (1) với các tham số . Trong trường hợp này . 
Mô hình có hai điểm cân bằng là ( và ( , trong đó là điểm cân bằng ổn định toàn 
cục, còn là điểm cân bằng không ổn định. 
Nghiệm số thu được từ các phương pháp Runge-Kutta bốn nấc kinh điển (classical four stage Runge–Kutta 
method), phương pháp Runge-Kutta hiển hai nấc (two stage Runge–Kutta method) và phương pháp Euler hiển (explicit 
Euler method) được biểu diễn lần lượt trong các Hình 1-3. Ta thấy rằng phương pháp Runge-Kutta bốn nấc không bảo 
toàn được tính chất nghiệm dương của mô hình. Phương pháp Runge-Kutta hai nấc và phương pháp Euler hiển có 
nghiệm dao động xung quanh điểm cân bằng với biên độ dao động tăng dần. Khi xem xét nghiệm của mô hình trên 
khoảng thời gian càng lớn thì dao động xảy ra càng mạnh. Nghiệm số thu được trong các trường hợp này không thể 
bảo toàn các tính chất của mô hình (1). Nói chung, các phương pháp sai phân bình thường như Runge-Kutta và Taylor 
chỉ bảo toàn tính chất của bài toán khi bước lưới được chọn đủ nhỏ. 
Nghiệm số thu được từ lược đồ (3) được biểu diễn trong Hình 4, ở đây ta chọn = 5. Trong hình mỗi cặp 
đường màu xanh và màu đỏ tương ứng với một cặp nghiệm và . Trường hợp này, lược đồ (3) bảo toàn các tính 
chất của mô hình (1). Tương tự như vậy, khi ta chọn bước lưới bất kỳ thì tính chất của mô hình vẫn được bảo toàn nhờ 
lược đồ (3). 
Hình 1. Phương pháp Runge-Kutta bốn nấc kinh điển với ( ( 
280 LƯỢC ĐỒ SAI PHÂN KHÁC THƯỜNG MÔ PHỎNG SỐ MÔ HÌNH SIÊU QUẦN THỂ: SỬ DỤNG ĐỊNH LÝ ỔN ĐỊNH LYAPUNOV 
Hình 2. Phương pháp Runge-Kutta hai nấc với ( ( 
Hình 3. Phương pháp Euler hiển với ( ( 
Hình 4. Lược đồ (3) với bước lưới 
Đặng Quang Á, Hoàng Mạnh Tuấn 281 
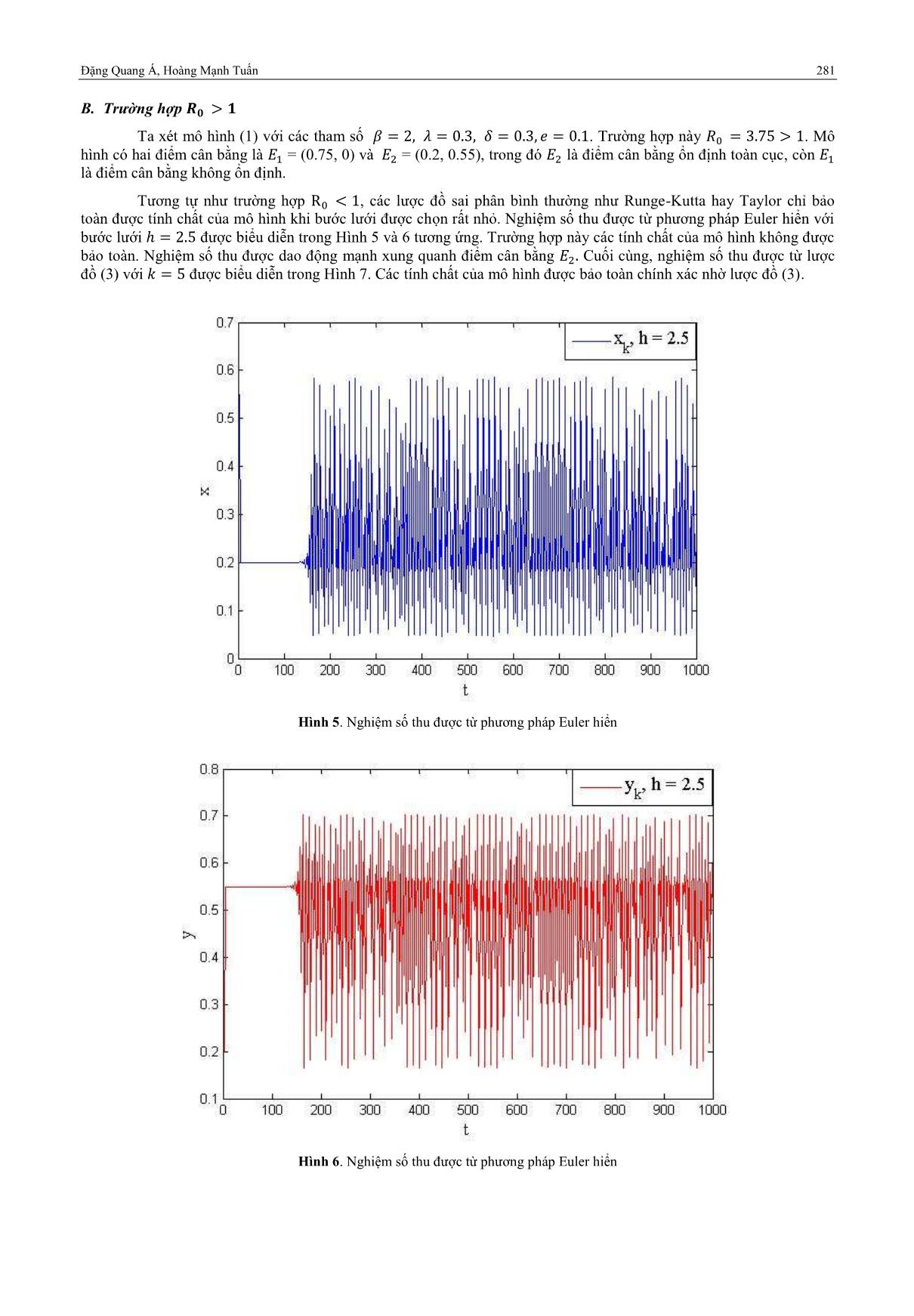
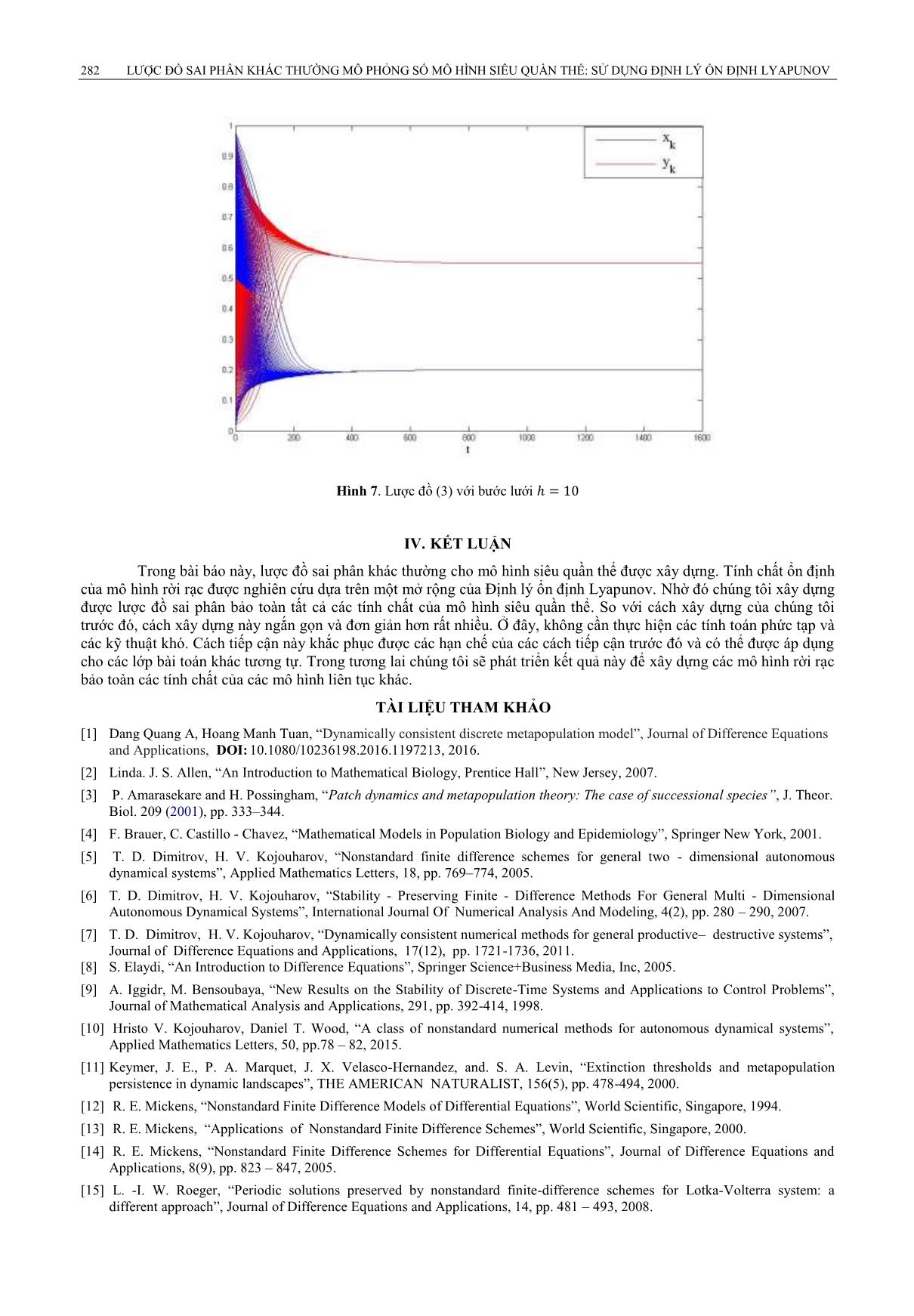
B. Trường hợp 
Ta xét mô hình (1) với các tham số . Trường hợp này . Mô 
hình có hai điểm cân bằng là = (0.75, 0) và = (0.2, 0.55), trong đó là điểm cân bằng ổn định toàn cục, còn 
là điểm cân bằng không ổn định. 
Tương tự như trường hợp , các lược đồ sai phân bình thường như Runge-Kutta hay Taylor chỉ bảo 
toàn được tính chất của mô hình khi bước lưới được chọn rất nhỏ. Nghiệm số thu được từ phương pháp Euler hiển với 
bước lưới được biểu diễn trong Hình 5 và 6 tương ứng. Trường hợp này các tính chất của mô hình không được 
bảo toàn. Nghiệm số thu được dao động mạnh xung quanh điểm cân bằng Cuối cùng, nghiệm số thu được từ lược 
đồ (3) với được biểu diễn trong Hình 7. Các tính chất của mô hình được bảo toàn chính xác nhờ lược đồ (3). 
Hình 5. Nghiệm số thu được từ phương pháp Euler hiển 
Hình 6. Nghiệm số thu được từ phương pháp Euler hiển 
282 LƯỢC ĐỒ SAI PHÂN KHÁC THƯỜNG MÔ PHỎNG SỐ MÔ HÌNH SIÊU QUẦN THỂ: SỬ DỤNG ĐỊNH LÝ ỔN ĐỊNH LYAPUNOV 
Hình 7. Lược đồ (3) với bước lưới 
IV. KẾT LUẬN 
Trong bài báo này, lược đồ sai phân khác thường cho mô hình siêu quần thể được xây dựng. Tính chất ổn định 
của mô hình rời rạc được nghiên cứu dựa trên một mở rộng của Định lý ổn định Lyapunov. Nhờ đó chúng tôi xây dựng 
được lược đồ sai phân bảo toàn tất cả các tính chất của mô hình siêu quần thể. So với cách xây dựng của chúng tôi 
trước đó, cách xây dựng này ngắn gọn và đơn giản hơn rất nhiều. Ở đây, không cần thực hiện các tính toán phức tạp và 
các kỹ thuật khó. Cách tiếp cận này khắc phục được các hạn chế của các cách tiếp cận trước đó và có thể được áp dụng 
cho các lớp bài toán khác tương tự. Trong tương lai chúng tôi sẽ phát triển kết quả này để xây dựng các mô hình rời rạc 
bảo toàn các tính chất của các mô hình liên tục khác. 
TÀI LIỆU THAM KHẢO 
[1] Dang Quang A, Hoang Manh Tuan, ―Dynamically consistent discrete metapopulation model‖, Journal of Difference Equations 
and Applications, DOI: 10.1080/10236198.2016.1197213, 2016. 
[2] Linda. J. S. Allen, ―An Introduction to Mathematical Biology, Prentice Hall‖, New Jersey, 2007. 
[3] P. Amarasekare and H. Possingham, ―Patch dynamics and metapopulation theory: The case of successional species”, J. Theor. 
Biol. 209 (2001), pp. 333–344. 
[4] F. Brauer, C. Castillo - Chavez, ―Mathematical Models in Population Biology and Epidemiology‖, Springer New York, 2001. 
[5] T. D. Dimitrov, H. V. Kojouharov, ―Nonstandard finite difference schemes for general two - dimensional autonomous 
dynamical systems‖, Applied Mathematics Letters, 18, pp. 769–774, 2005. 
[6] T. D. Dimitrov, H. V. Kojouharov, ―Stability - Preserving Finite - Difference Methods For General Multi - Dimensional 
Autonomous Dynamical Systems‖, International Journal Of Numerical Analysis And Modeling, 4(2), pp. 280 – 290, 2007. 
[7] T. D. Dimitrov, H. V. Kojouharov, ―Dynamically consistent numerical methods for general productive– destructive systems‖, 
Journal of Difference Equations and Applications, 17(12), pp. 1721-1736, 2011. 
[8] S. Elaydi, ―An Introduction to Difference Equations‖, Springer Science+Business Media, Inc, 2005. 
[9] A. Iggidr, M. Bensoubaya, ―New Results on the Stability of Discrete-Time Systems and Applications to Control Problems‖, 
Journal of Mathematical Analysis and Applications, 291, pp. 392-414, 1998. 
[10] Hristo V. Kojouharov, Daniel T. Wood, ―A class of nonstandard numerical methods for autonomous dynamical systems‖, 
Applied Mathematics Letters, 50, pp.78 – 82, 2015. 
[11] Keymer, J. E., P. A. Marquet, J. X. Velasco-Hernandez, and. S. A. Levin, ―Extinction thresholds and metapopulation 
persistence in dynamic landscapes‖, THE AMERICAN NATURALIST, 156(5), pp. 478-494, 2000. 
[12] R. E. Mickens, ―Nonstandard Finite Difference Models of Differential Equations‖, World Scientific, Singapore, 1994. 
[13] R. E. Mickens, ―Applications of Nonstandard Finite Difference Schemes‖, World Scientific, Singapore, 2000. 
[14] R. E. Mickens, ―Nonstandard Finite Difference Schemes for Differential Equations‖, Journal of Difference Equations and 
Applications, 8(9), pp. 823 – 847, 2005. 
[15] L. -I. W. Roeger, ―Periodic solutions preserved by nonstandard finite-difference schemes for Lotka-Volterra system: a 
different approach‖, Journal of Difference Equations and Applications, 14, pp. 481 – 493, 2008. 
Đặng Quang Á, Hoàng Mạnh Tuấn 283 
[16] L. -I. W. Roeger, ―Nonstandard finite-difference schemes for the Lotka-Volterra systems: generalization of Mickens's 
method‖, Journal of Difference Equations and Applications , 12, pp. 937 – 948, 2006. 
[17] Alexander A. Samarskii, ―The theory of difference schemes‖, Marcel Dekker, Inc, 2001. 
[18] D. T. Wood, T. D. Dimitrov, H. V. Kojouharov, ―A nonstandard finite difference method for n-dimensional productive-
destructive systems‖, Journal of Difference Equations and Applications, DOI: 10.1080/10236198.2014.997228, 2015. 
NONSTANDARD FINITE DIFFERENCE SCHEMES FOR NUMERICAL 
 SIMULATION OF A METAPOPULATION MODEL: USING THE 
LYAPUNOV STABILITY THEOREM 
Dang Quang A, Hoang Manh Tuan 
ABSTRACT — In this paper nonstandard finite difference (NSFD) schemes for a metapopulation model are constructed. The 
stability properties of the discrete models are investigated by the use of a generalization of Lyapunov stability theorem. Due to this 
result we have proved that the NSFD schemes preserve all properties of the metapopulation model. Numerical examples confirm the 
obtained theoretical results of the properties of the constructed difference schemes. The method of Lyapunov functions proves to be 
much simpler than the standard method for studying stability of the discrete metapopulation model in our very recent paper.