L+l- → γh collision in the randall – sundrum model
The production of the Higgs boson and photon from the l l + − collision when
beams l l + − , are unpolarized and polarized are studied in detail in the Randall –
Sundrum model (RS). Based on the results, we show that the advantageous direction to
observe Higgs boson is the same direction of the lepton l− or antilepton l+ .And at the
high energy region, the total cross-section changed very small when the collision energy
s increased. We also obtained the value of cross section of the Higgs boson production
in e e + − collision is smaller than µ µ + − collision.

Trang 1

Trang 2

Trang 3

Trang 4
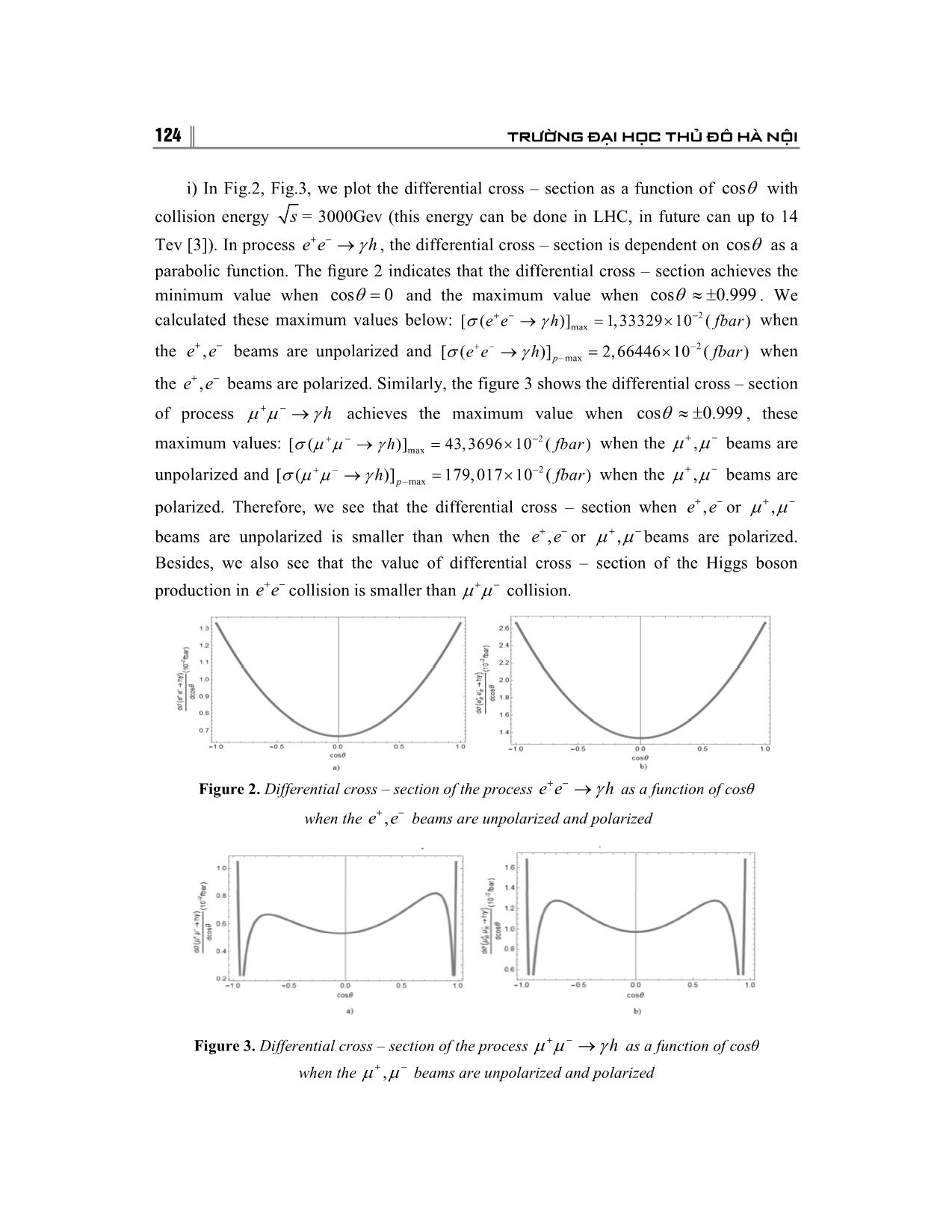
Trang 5
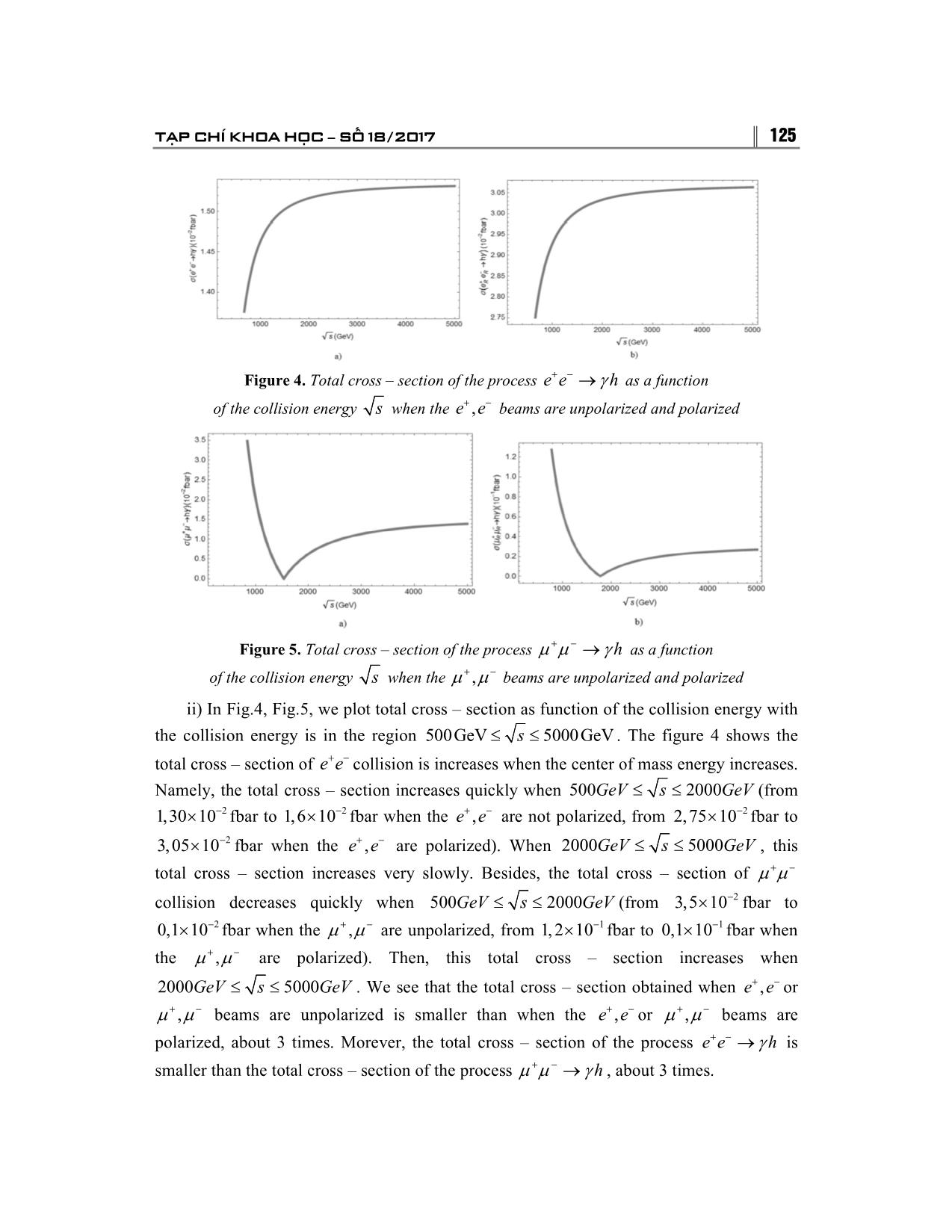
Trang 6

Trang 7
Bạn đang xem tài liệu "L+l- → γh collision in the randall – sundrum model", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: L+l- → γh collision in the randall – sundrum model

120 TRƯỜNG ĐẠI HỌC THỦ ĐÔ H� NỘI l+ l − → γ h COLLISION IN THE RANDALL – SUNDRUM MODEL Dao Thi Le Thuy 1, Le Nhu Thuc 1 Nguyen Thi Nhung 2, Dang Trong Hoa 2 1Hanoi National University of Education 2Graduate students – 26 th course – Faculty of Physics – HNUE AbstractAbstract: The production of the Higgs boson and photon from the l+ l − collision when beams l+, l − are unpolarized and polarized are studied in detail in the Randall – Sundrum model (RS). Based on the results, we show that the advantageous direction to observe Higgs boson is the same direction of the lepton l− or antilepton l+ ... And at the high energy region, the total cross�section changed very small when the collision energy s increased. We also obtained the value of cross section of the Higgs boson production in e+ e − collision is smaller than �+ � − collision. KeywordsKeywords: lepton, Higgs, Randall – Sundrum model. Email: thuydtl@hnue.edu.vn Received 15 July 2017 Accepted for publication 10 September 2017 1. INTRODUCTION Almost all existing experimental data is described successfully by the Standard Model of electroweak. However this model suffers from many theoretical drawbacks, one of these is the hierarchy problem. Namely, the Standard Model can not consistently accommodate the weak energy scale (about 1 Tev) and a much higher scale such as the Planck scale (about 10 19 GeV). Therefore, it is commonly believed that the Standard Model is only an effective theory emergings as the low – energy limit of some more fundamental high – scale theory. Recently, it was pointed out that the existence of extra – dimensions could be a solution of the hierarchy problem [7]. The Randall – Sundrum model (RS) is one of the most attractive attempts [1]. RS was given by Randall and Sundrum in 1999 to solve the hierarchy problem of the Standard Model. It involves a finite five – dimensional bulk that is extremely warp and contains two branes: the Planck brane (also called Gravity brane – where gravity is a relatively strong force) and TeV brane (also called weak brane, studied with the Standard Model particles). In this model, the two branes are separated in the not – necessarily large fifth dimension by approximately 16 units (the units based on the brane and bulk energies). The Planck brane has positive brane energy, and the Tevbrane has negative brane energy. TẠP CHÍ KHOA HỌC −−− SỐ 18/2017 121 These energies are the cause of the extremely warped spacetime. In this warped spacetime that is only warped along the fifth dimension, the graviton's probability function is extremely high at the Planck brane, but it drops exponentially as it moves closer towards the TeV brane. In this, gravity would be much weaker on the TeV brane than on the Planck brane. In order to obtain a consistent solution to the Einstein equations corresponding to a low – energy effective theory on the visible brane with a flat metric, the branes must have equal but opposite cosmological constants and these must be precisely related to the bulk cosmological constant. The RS is defined by the 5D action [1]: 4 R S=−∫ d xdy − g ˆ +Λ 16 πG5 +−dxg4 L −+ V dxg4 − L − V , (1) ∫hid( hid hid) ∫ vis( vis vis ) where gˆ �ˆv ˆ is the bulk metric with �ˆ, vˆ = 0, 4 , and 4 refers to the y coordinate; when y = 0, �v the bulk metric with the hidden brane is ghid ( x ), and when y=1/2, the bulk metric with the �v visible brane is gvis ( x ) (� ,v = 0, 1, 2, 3) . The 5 – dimensional warped metric is given by [1]: ds2= e− 2()σyη dx � dx v − b 22 dy , (2) �v 0 Where σ()ymby=0 0 [ (2()1) θ y −−− 2( y 1/2)( θ y − 1/2) ] and b 0 is a constant parameter. Gravitational fluctuations around the above background metric will be defined through the replacements: η→+ η ε h( xyb , ); →+ b bx ( ). (3) �v � v � v 0 0 Based on the theories of Randall – Sundrum model, we have necessary constants to complete next section. In this paper, we study the production of the Higgs boson and photon at e+ e − , �+ � − collider. This paper is organized as follows: In Sec.2, we have interaction vertices between lepton, antilepton, photon and Higgs boson in the Randall Sundrum model. In addition, we also calculate results from production of the Higgs boson in the collider and show our numerical results with discussion. And our conclusions in Sec.3. 2. l+ l − → γ h COLLISIONS IN RANDALL – SUNDRUM MODEL We are interested in the production of Higgs boson and photon from the l+, l − colliders in the high energy, 122 TRƯỜNG ĐẠI HỌC THỦ ĐÔ H� NỘI r r r r l−(p)+ l + (p) → hk () + γ () k (4) 1 2 1 2 r r Here pi, k i stand for the momentum of the particle, respectively. There are three Feynman diagrams contributing to reaction (4), representing the s, u, t – channel exchange depicted in Figure 1. Figure 1. The Feynman diagrams l+ l − → γ h collision. Use Feynman rules, the matrix element for process l+ l − → γ h can be written as the following cases: + For s – channel: e. c r r r M=− iγ [( kqgkq )να −× ν α ]ε* ()v(p) k γ up () , (5) sq 2 2 s 2 s α 221 ν s e. c r r r M=−iγ [( kqgkq )να −× ν α ]ε* ()v(p)(1 k + γ )() γ up , (6) sLL2q 2 2 s 2 s α 2251 ν s e. c r r r M=− iγ [( kqgkq )να −× ν α ]ε* ( k ) v(p )(1 − γ ) γ up ( ) , (7) sRR2q 2 2 s 2 s α 2251 ν s + For u – channel: e. g . m r r r M=− ie ( dbkvp +γ )()()( ε* γ ν qmupˆ + )() , (8) u 2m ( q2+ m 2 ) ν 2 2u e 1 w u e e. g . m 2 r r r M=−ie ( dbkvp +γε )()()(1)()* + γγ ν up , (9) uLL 4m ( q2+ m 2 ) ν 22 5 1 w u e e. g . m 2 r r r M=−ie ( dbkvp +γε )()()(1)()* − γγ ν up , (10) uRR 4m ( q2+ m 2 ) ν 22 5 1 w u e e. g . m r r r M=−ie ( dbkvp +γε )()()(1)* + γγ ν qupˆ () , (11) uLR 4m ( q2+ m 2 ) ν 22 5u 1 w u e e. g . m r r r M=−ie ( dbkvp +γε )()()(1)* − γγ ν qupˆ () . (12) uRL 4m ( q2+ m 2 ) ν 22 5u 1 w u e TẠP CHÍ KHOA HỌC −−− SỐ 18/2017 123 + For t – channel: e. g . m r r r M=− ie ( dbkvpqmup +γ )()()( ε* ˆ + ) γ � () , (13) t 2m ( q2+ m 2 ) � 2 2t e 1 w t e e. g . m 2 r r r M=−ie ( dbkvp +γε )()()(1)()* + γγ � up , (14) tLL 4m ( q2+ m 2 ) � 22 5 1 w t e e. g . m 2 r r r M=−ie ( dbkvp +γε )()()(1)()* − γγ � up , (15) tRR 4m ( q2+ m 2 ) � 22 5 1 w t e e. g . m r r r M=−ie ( dbkvp +γε )()()(1)q* + γγˆ � up () , (16) tLR 4m ( q2+ m 2 ) � 22 5t 1 w t e e. g . m r r r M=−ie ( dbkvp +γε )()()(1)q* − γγˆ � up () . (17) tRL 4m ( q2+ m 2 ) � 22 5t 1 w t e Using these matrix elements, we evaluate the differential and total cross – section for Higgs boson and photon production in the l+ l − collider in the next section. In this section, we present the numerical results for differential and total cross – section for Higgs boson production in the e+ e − , �+ � − collider when the e+, e − , �+, � − beams are polarized and not polarized. We use the expression of the cross – section: r dσ 1 k 2 = r M , (18) d(cosθ ) 64 π 2 s p with M is the matrix element, d� = d(cosθ ) d ϕ ; θ∈ [0, π ] ; ϕ∈[0,2 π ] . We assess the number, make the identification and evaluation of the results obtained from the dependence of the differential cross – section by cos θ and the total cross – section fully follows s . We choose: m =0,00051 GeV; m = 80 GeV; m = 0 ; m = 0,1055 GeV; e w γ � 1 m = 120 GeV; α = , e= 4πα ; g = 0.634 ; ξ =1/ 6 ; h 137 12 γξ Z m 2 Z =16 +ξγ2 16 − ξ ; tan 2θ = h ; ( ()) 22 22 2 mh () Z−36 ξ γ − m φ cos θ 6ξγ a = ; c =sinθ − cos θ . Z Z We obtain some estimates for the cross – section as following: 124 TRƯỜNG ĐẠI HỌC THỦ ĐÔ H� NỘI i) In Fig.2, Fig.3, we plot the differential cross – section as a function of cos θ with collision energy s = 3000Gev (this energy can be done in LHC, in future can up to 14 Tev [3]). In process e+ e − → γ h , the differential cross – section is dependent on cos θ as a parabolic function. The figure 2 indicates that the differential cross – section achieves the minimum value when cosθ = 0 and the maximum value when cos θ ≈ ± 0.999 . We + − − 2 calculated these maximum values below: [(σee→ γ h )]max = 1,3332910( × fbar ) when + − + − − 2 the e, e beams are unpolarized and [(σee→ γ h )]p−max = 2,6644610( × fbar ) when the e+, e − beams are polarized. Similarly, the figure 3 shows the differential cross – section of process �+ � − → γ h achieves the maximum value when cos θ ≈ ± 0.999 , these + − − 2 + − maximum values: [(σ��→ γ h )]max = 43,369610( × fbar ) when the �, � beams are + − − 2 + − unpolarized and [(σ��→ γ h )]p−max = 179,01710( × fbar ) when the �, � beams are polarized. Therefore, we see that the differential cross – section when e+, e − or �+, � − beams are unpolarized is smaller than when the e+, e − or �+, � − beams are polarized. Besides, we also see that the value of differential cross – section of the Higgs boson production in e+ e − collision is smaller than �+ � − collision. Figure 2. Differential cross – section of the process e+ e − → γ h as a function of cosθ when the e+, e − beams are unpolarized and polarized Figure 3. Differential cross – section of the process �+ � − → γ h as a function of cosθ when the �+, � − beams are unpolarized and polarized TẠP CHÍ KHOA HỌC −−− SỐ 18/2017 125 Figure 4. Total cross – section of the process e+ e − → γ h as a function of the collision energy s when the e+, e − beams are unpolarized and polarized Figure 5. Total cross – section of the process �+ � − → γ h as a function of the collision energy s when the �+, � − beams are unpolarized and polarized ii) In Fig.4, Fig.5, we plot total cross – section as function of the collision energy with the collision energy is in the region 500GeV≤s ≤ 5000GeV . The figure 4 shows the total cross – section of e+ e − collision is increases when the center of mass energy increases. Namely, the total cross – section increases quickly when 500GeV≤ s ≤ 2000 GeV (from 1,30× 10 −2 fbar to 1,6× 10 −2 fbar when the e+, e − are not polarized, from 2,75× 10 −2 fbar to 3,05× 10 −2 fbar when the e+, e − are polarized). When 2000GeV≤ s ≤ 5000 GeV , this total cross – section increases very slowly. Besides, the total cross – section of �+ � − collision decreases quickly when 500GeV≤ s ≤ 2000 GeV (from 3,5× 10 −2 fbar to 0,1× 10 −2 fbar when the �+, � − are unpolarized, from 1,2× 10 −1 fbar to 0,1× 10 −1 fbar when the �+, � − are polarized). Then, this total cross – section increases when 2000GeV≤ s ≤ 5000 GeV . We see that the total cross – section obtained when e+, e − or �+, � − beams are unpolarized is smaller than when the e+, e − or �+, � − beams are polarized, about 3 times. Morever, the total cross – section of the process e+ e − → γ h is smaller than the total cross – section of the process �+ � − → γ h , about 3 times. 126 TRƯỜNG ĐẠI HỌC THỦ ĐÔ H� NỘI 3. CONCLUSION In this paper, the production of the Higgs boson and photon in the l+ l − collider when the l+, l − beams are polarized and unpolarized are calculated, we have obtailed that the differential cross – section and total cross – section of the the Higgs boson production when the l+, l − beams are unpolarized is smaller than the l+, l − beams are polarized. The value of cross – section obtained in e+ e − collision is smaller than �+ � − collision. Althought that, the cross – sections are very small, about 10 �2 fbar. We also showed that the advantageous direction to see Higgs boson is parallel direction of the initial lepton beam with the antilepton beam. REFERENCES 1. D. Dominici, B. Grzadkowski, J. F. Gunion and M. Toharia (2003), “The Scalar sector of the Randall – Sundrum model”, Nucl. Phys . B 671, p.243, [arXiv:hep – ph/0206192]. 2. Dao Thi Le Thuy, Bui Thi Ha Giang (2016), “ e+ e − → hZ collision in Randall – Sundrum model”, Communications in Physics, Vol.26, No.1 (2016), pp.19–24. 3. E. S. Reich (2013), “Physicists plant to build a bigger LHC”, Nature News, Nature Publishing Group , Nov 12. 4. L. Randall and R. Sundrum (1999), Phys. Rev . Lett. 83, p.3370. 5. Maxime Gabella (June – 2006), The Randall – Sundrum Model , University of Oxford. 6. M. Beneke, P. Moch, J. Rohrwild (2016), “ Lepton flavor violation in RS models with a brane – or nearly brane – localized Higgs”, Nuclear Physics B 906 (2016) pp.561–614. 7. Ryuichiro Kitano1, (2000), “ Lepton Flavor Violation in the Randall – Sundrum Model with Bulk Neutrinos”, [arXiv:hep – ph/0002279v2 16 Mar 2000]. S� VA CH�M l+ l − →γ h TRONG MÔ HÌNH RANDALL – SUNDRUM Tóm tt�t�t�t�t: Quá trình sinh Higgs boson và photon t� va ch�m l+ l − khi chùm l+, l − không phân c�c và phân c�c trong mô hình Randall – Sundrum (RS) ñư�c chúng tôi tính toán chi ti�t, t� ñó ch� ra ñư�c hư�ng có l�i ñ� thu ñư�c tín hi�u c�a Higgs trong cùng hư�ng v�i hư�ng c�a chùm lepton ho�c ph�n lepton ban ñ�u. Trong mi�n năng lư�ng cao, khi năng lư�ng va ch�m tăng thì ti�t di�n tán x� ít thay ñ�i, bên c�nh ñó chúng tôi cũng ch� ra ñư�c giá tr� ti�t di�n tán x� c�a s� sinh Higgs t� va ch�m e+ e − nh� hơn va ch�m �+ � − . T� khóakhóa: H�t Lepton, trư�ng Higgs, mô hình Randall�Sundrum
File đính kèm:
 ll_h_collision_in_the_randall_sundrum_model.pdf
ll_h_collision_in_the_randall_sundrum_model.pdf

