Khai thác tập phổ biến có trọng số dựa trên cấu trúc N-list

 phần tiền tố là X, trong 
đó A xếp sau B theo thứ tự trong I1. WL(XA) và WL(XB) là hai WN-list tương ứng của XA và XB. Ta có WL(XAB) là 
WN-list của k-itemset XAB được xác định như sau: 
1. Với mỗi cặp Ci(xi, yi, wi) WL(XA) và Cj(xj, yj, wj) WL(XB), nếu Cj là tổ tiên của Ci thì ta thêm (xj, yj, wi) 
vào WL(XAB). 
2. Duyệt WL(XAB) và tổ hợp các WN-code có cùng (pre, post) thành một WN-code mới có trọng số là tổng 
của các giá trị trọng số trong các WN-code đang xét. 
Dựa vào Định nghĩa 8 ta dễ dàng xây dựng được Thuật toán 2 (WL_Intersection) thực hiện phép giao giữa 
hai WN-list với độ phức tạp tuyến tính. 
Định lý 2. Cho X là một itemset với WN-list của X là WL(X) = . Độ 
phổ biến trọng số của X là được tính như sau: 
∑ 
∑ 
 (3) 
Chứng minh: Không mất tính tổng quát, ta giả sử itemset X = A1A2...Am, trong đó Ai đứng sau Ai+1 theo thứ tự 
trong I1. Theo cách xác định WN-list trong định nghĩa 7, ta có: 
(a) Với mỗi WN-code Ci(xi, yi, wi) WL(X), tồn tại một nút trên cây WN có item-name = Am, pre = xi và pos = 
yi tương ứng với (xi, yi). 
(b) wi là tổng các weight của các nút có item-name = A1 trong cây con thuộc cây WN có gốc là Am trong (a). 
Gọi Ti là tập các giao dịch chứa X đi qua cây con có gốc là Am(pre = xi, pos = yi), lúc đó mỗi Ti sẽ tương ứng 
với một WN-code (xi, yi, wi) và theo (a) và (b) ta có: 
 ∑ 
(c) 
 ⋃ 
(d) 
Theo công thức (2), (c) và (d) ta có: 
∑ 
∑ 
∑ ∑ 
∑ 
∑ 
∑ 
Định lý 2 đã được chứng minh. 
IV. THUẬT TOÁN NFWI KHAI THÁC FWI TRÊN WD 
Chúng tôi sử dụng cây liệt kê (set-enumeration tree) [16] để đơn giản hóa quá trình duyệt khai thác FWI. Cụ 
thể, với CSDL ví dụ trong Bảng 2, ta có cây liệt kê như Hình 2. 
Hình 2. Cây liệt kê của CSDL trong Bảng 2 
Vận dụng các định nghĩa và định lý đã trình bày ở phần trước, chúng tôi đề xuất thuật toán NFWI để khai thác 
FWI trên WD như Hình 3. 
Thuật toán 3: Thuật toán NFWI 
Input: CSDL có trọng số WD và ngưỡng minws 
Output: FWI, là tập tất cả các tập phổ biến có trọng số. 
Method name: NFWI_Algorithm(WD, minws) 
1. Call Construction_WN_Tree(WD, minws) to generate Tree and I1 
2. Scan Tree to generate WN-lists of items in I1 
3. Let FWI I1 
4. Call Find_FWI(I1, ) 
5. return FWI 
Bùi Danh Hường, Võ Đình Bảy, Nguyễn Duy Hàm 251 
Procedure Find_FWI(Lk,Prek) 
6. Prenext = Prek 
7. for i = Lk.size downto 2 do 
8. Prenext i 
9. Lnext = 
10. for j = i-1 downto 1 do 
11. WLij = WL_Intersection(WLi, WLj) 
12. if ws(WLij) minws then 
13. FWI {Prek {Li} {Lj}} 
14. Inext Li 
15. if Lnext then Find_FWI(Lnext, Prenext) 
16. remove last item of Prenext 
Hình 3. Thuật toán NFWI 
Thuật toán NFWI hoạt động như sau: đầu tiên xây dựng cây WN và phát sinh WN-list của các 1-FWI. Tiếp đó 
duyệt theo cây liệt kê và áp dụng thuật toán giao hai WN-list để xác định WN-list của một k-itemset từ WN-list của hai 
(k-1)-itemset tương ứng. Trong quá trình tính toán WN-list, áp dụng định lý 2 để tìm và cập nhật tập FWI. 
Chi tiết của thuật toán NFWI được thể hiện ở trong Thuật toán 3. Sau khi xây dựng cây WN và phát sinh tập 
các 1-FWI là I1, thì gọi hàm Find_FWI(Lk, Prek) để bắt đầu tiến trình xử lý khai thác FWI. Ở đây, Lk là tập các item 
cuối và Prek là tập các tiền tố giống nhau của các itemset thuộc về lớp hiện tại. Dòng 4 thể hiện thời điểm gọi hàm 
Find_FWI lần đầu tiên, trong đó Lk = I1 và Prek = . Dòng 6, 8, 9, 14 và 16 là nơi khai báo và tính toán các biến mới là 
Lnext và Prenext, các biến này được sử dụng làm tham số để gọi hàm đệ quy cho lớp tìm kiếm tiếp theo (Dòng 15). Ở 
dòng 7-14, thuật toán thực hiện phép giao của mọi cặp WN-lists của các k-itemset có trong Ik, sau đó so sánh giá trị ws 
của (k+1)-itemset thu được với ngưỡng, và phụ thuộc vào kết quả so sánh để cập nhật tập FWI và Lnext (Dòng 13-14). 
Ví dụ 3. Chúng ta sẽ minh họa hoạt động của thuật toán NFWI với CSDL ví dụ ở trong Bảng 2. Sau khi gọi 
hàm Construction_WN_Tree ta thu được kết quả là cây WN như Hình 1 với tập I1 = {B, E, A, D, C}, minws = 0.5, 
sumtw = 2.4. 
Từ cây WN và I1 ta sinh ra được WN-list cho các 1-FWI như sau: 
WL(C) = {(5, 0, 0.5), (6, 2, 0.4), (8, 4, 0.4)} 
WL(D) = {(4, 1, 1), (7, 5, 0.4)} 
WL(A) = {(3, 3, 1.4), (9, 7, 0.4)} 
WL(E) = {(2, 6, 2)} 
WL(B) = {(1, 8, 2.4)} 
Cập nhật các 1-FWI vào tập FWI: 
FWI = {B, E, A, D, C} 
Duyệt theo các nhánh của cây liệt kê (Hình 2) từ trái qua phải, ta lần lượt khai thác FWI theo tiến trình như 
sau: 
Khởi đầu với L1 = {B, E, A, D, C}, Pre1 = , S1 = 
 Đi theo nhánh C: Pre2 = {C} 
WL(CD) = {(4, 1, 0.5), (7, 5, 0.4)} 
WL(CA) = {(3, 3, 0.5), (3, 3, 0.4)} = {(3, 3, 0.9)} 
WL(CE) = {(2, 6, 0.5), (2, 6, 0.4), (2, 6, 0.4)} = {(2, 6, 1.3)} 
WL(CB) = {(1, 8, 0.5), (1, 8, 0.4), (1, 8, 0.4)} = {(1, 8, 1.3)} 
Do ws(CD) = (0.5+0.4)/2.4 = 0.9/2.4<minws = 0.5 nên CD không phải là FWI. Tương tự như vậy, CA cũng 
không phải là FWI. 
Do ws(CE) = ws(CB) = ws(C) = 1.3/2.4 > 0.5 nên cập nhật FWI và L2 = {E, B}: 
FWI = {B, E, A, D, C, CE, CB} 
o Bởi vì L2 = {E, B} nên gọi đệ quy đến hàm Find_FWI(L2 = {E, B}, Pre2 = {C}). 
WL(CEB) = {(1, 8, 1.3)} 
Bởi vì ws(CEB) = 1.3/2.4 > 0.5 nên cập nhật FWI: 
252 KHAI THÁC TẬP PHỔ BIẾN CÓ TRỌNG SỐ DỰA TRÊN CẤU TRÚC N-LIST 
FWI = {B, E, A, D, C, CE, CB, CEB} 
Thực hiện tương tự với các nhánh D, A và E, ta nhận được kết quả cuối cùng như sau: 
FWI = {B, E, A, D, C, CE, CB, CEB, DE, DB, DEB, AE, AB, AEB, EB} 
V. THỰC NGHIỆM VÀ ĐÁNH GIÁ 
Tất cả các thử nghiệm trong phần tiếp theo đều được tiến hành trên cùng một hệ thống CPU Intel Core i5 2.5 
GHz, bộ nhớ Ram 8GBs, chạy trên hệ điều hành Windows 7, sử dụng ngôn ngữ lập trình Visual C# 2012. 
Chúng tôi thực nghiệm trên các CSDL Accidents, Connect, Retail và BMS-POS, được download từ 
 và biến đổi bằng cách thêm bảng lưu trữ trọng số của các item (ngẫu nhiên trong khoảng 
1 đến 10). Chúng tôi so sánh thuật toán NFWI với các thuật toán khai thác FWI mới nhất là WIT-FWIs-Diff [14] và 
IWS [15], trong đó WIT-FWIs-Diff được đánh giá hiệu quả trên các CSDL dày, còn IWS thì hiệu quả hơn trên các 
CSDL thưa. 
Bảng 3. Một số thông số về các CSDL dùng thử nghiệm 
CSDL 
Số lượng 
items 
Số lượng 
giao dịch 
Độ dài trung bình của 
giao dịch 
Ghi chú 
Accidents 468 340,183 33.8 Modified 
Connect 130 67,557 43 Modified 
Retail 16,470 88,162 10.3 Modified 
BMS-POS 1,657 515,597 6.5 Modified 
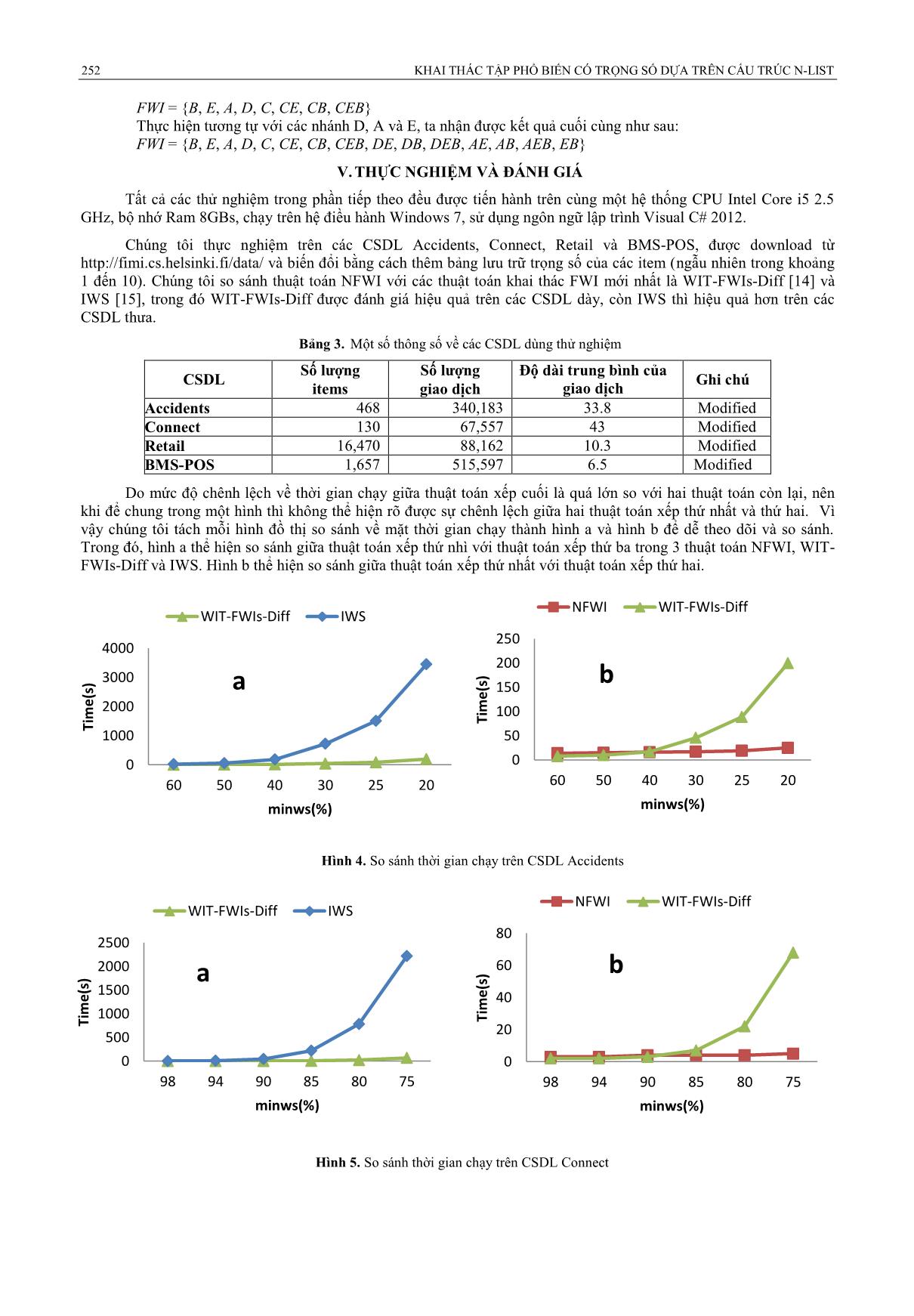
Do mức độ chênh lệch về thời gian chạy giữa thuật toán xếp cuối là quá lớn so với hai thuật toán còn lại, nên 
khi để chung trong một hình thì không thể hiện rõ được sự chênh lệch giữa hai thuật toán xếp thứ nhất và thứ hai. Vì 
vậy chúng tôi tách mỗi hình đồ thị so sánh về mặt thời gian chạy thành hình a và hình b để dễ theo dõi và so sánh. 
Trong đó, hình a thể hiện so sánh giữa thuật toán xếp thứ nhì với thuật toán xếp thứ ba trong 3 thuật toán NFWI, WIT-
FWIs-Diff và IWS. Hình b thể hiện so sánh giữa thuật toán xếp thứ nhất với thuật toán xếp thứ hai. 
Hình 4. So sánh thời gian chạy trên CSDL Accidents 
Hình 5. So sánh thời gian chạy trên CSDL Connect 
0
1000
2000
3000
4000
60 50 40 30 25 20
Ti
m
e
(s
) 
minws(%) 
a 
WIT-FWIs-Diff IWS
0
50
100
150
200
250
60 50 40 30 25 20
Ti
m
e
(s
) 
minws(%) 
b 
NFWI WIT-FWIs-Diff
0
500
1000
1500
2000
2500
98 94 90 85 80 75
Ti
m
e
(s
) 
minws(%) 
a 
WIT-FWIs-Diff IWS
0
20
40
60
80
98 94 90 85 80 75
Ti
m
e
(s
) 
minws(%) 
b 
NFWI WIT-FWIs-Diff
Bùi Danh Hường, Võ Đình Bảy, Nguyễn Duy Hàm 253 
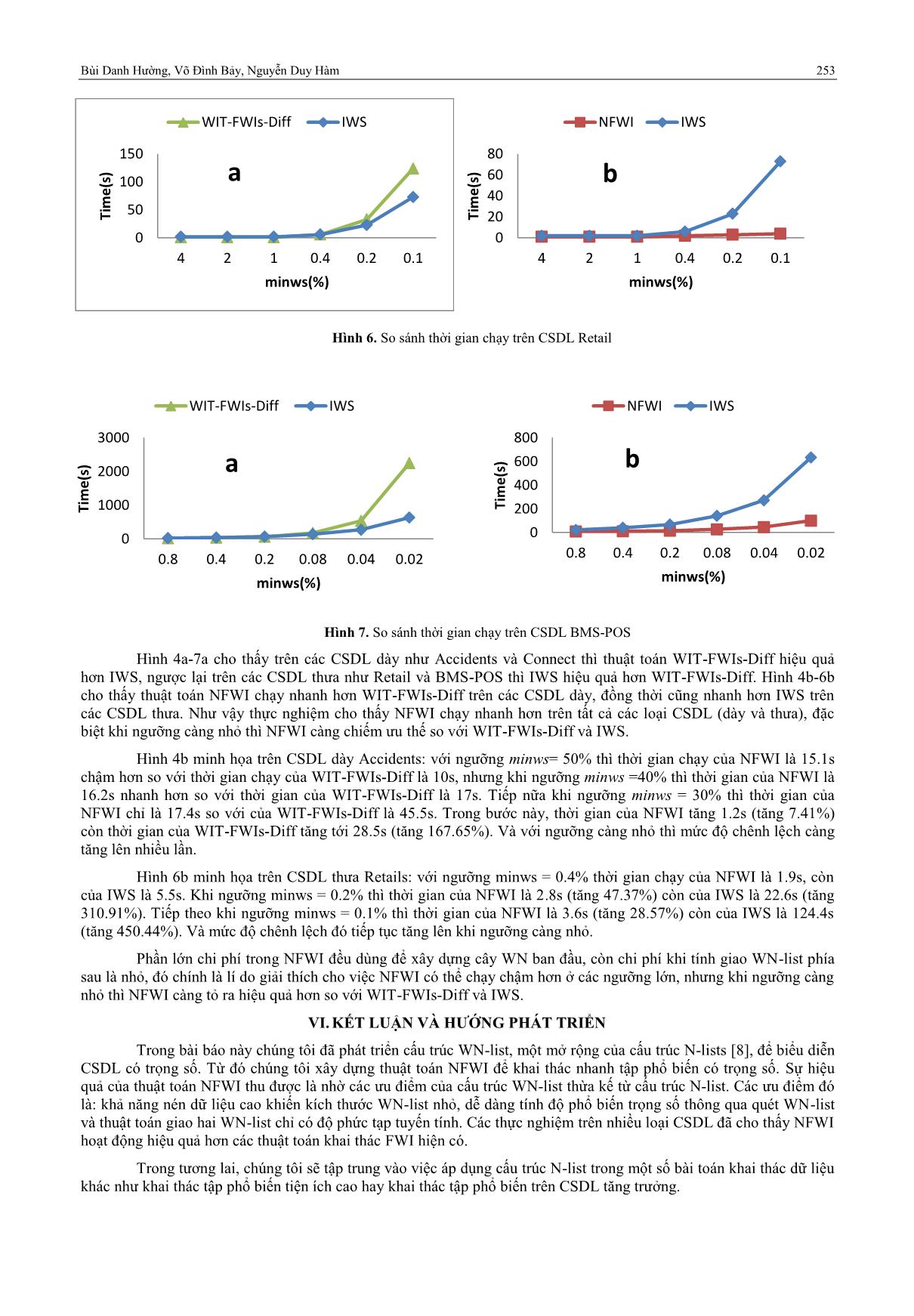
Hình 6. So sánh thời gian chạy trên CSDL Retail 
Hình 7. So sánh thời gian chạy trên CSDL BMS-POS 
Hình 4a-7a cho thấy trên các CSDL dày như Accidents và Connect thì thuật toán WIT-FWIs-Diff hiệu quả 
hơn IWS, ngược lại trên các CSDL thưa như Retail và BMS-POS thì IWS hiệu quả hơn WIT-FWIs-Diff. Hình 4b-6b 
cho thấy thuật toán NFWI chạy nhanh hơn WIT-FWIs-Diff trên các CSDL dày, đồng thời cũng nhanh hơn IWS trên 
các CSDL thưa. Như vậy thực nghiệm cho thấy NFWI chạy nhanh hơn trên tất cả các loại CSDL (dày và thưa), đặc 
biệt khi ngưỡng càng nhỏ thì NFWI càng chiếm ưu thế so với WIT-FWIs-Diff và IWS. 
Hình 4b minh họa trên CSDL dày Accidents: với ngưỡng minws= 50% thì thời gian chạy của NFWI là 15.1s 
chậm hơn so với thời gian chạy của WIT-FWIs-Diff là 10s, nhưng khi ngưỡng minws =40% thì thời gian của NFWI là 
16.2s nhanh hơn so với thời gian của WIT-FWIs-Diff là 17s. Tiếp nữa khi ngưỡng minws = 30% thì thời gian của 
NFWI chỉ là 17.4s so với của WIT-FWIs-Diff là 45.5s. Trong bước này, thời gian của NFWI tăng 1.2s (tăng 7.41%) 
còn thời gian của WIT-FWIs-Diff tăng tới 28.5s (tăng 167.65%). Và với ngưỡng càng nhỏ thì mức độ chênh lệch càng 
tăng lên nhiều lần. 
Hình 6b minh họa trên CSDL thưa Retails: với ngưỡng minws = 0.4% thời gian chạy của NFWI là 1.9s, còn 
của IWS là 5.5s. Khi ngưỡng minws = 0.2% thì thời gian của NFWI là 2.8s (tăng 47.37%) còn của IWS là 22.6s (tăng 
310.91%). Tiếp theo khi ngưỡng minws = 0.1% thì thời gian của NFWI là 3.6s (tăng 28.57%) còn của IWS là 124.4s 
(tăng 450.44%). Và mức độ chênh lệch đó tiếp tục tăng lên khi ngưỡng càng nhỏ. 
Phần lớn chi phí trong NFWI đều dùng để xây dựng cây WN ban đầu, còn chi phí khi tính giao WN-list phía 
sau là nhỏ, đó chính là lí do giải thích cho việc NFWI có thể chạy chậm hơn ở các ngưỡng lớn, nhưng khi ngưỡng càng 
nhỏ thì NFWI càng tỏ ra hiệu quả hơn so với WIT-FWIs-Diff và IWS. 
VI. KẾT LUẬN VÀ HƯỚNG PHÁT TRIỂN 
Trong bài báo này chúng tôi đã phát triển cấu trúc WN-list, một mở rộng của cấu trúc N-lists [8], để biểu diễn 
CSDL có trọng số. Từ đó chúng tôi xây dựng thuật toán NFWI để khai thác nhanh tập phổ biến có trọng số. Sự hiệu 
quả của thuật toán NFWI thu được là nhờ các ưu điểm của cấu trúc WN-list thừa kế từ cấu trúc N-list. Các ưu điểm đó 
là: khả năng nén dữ liệu cao khiến kích thước WN-list nhỏ, dễ dàng tính độ phổ biến trọng số thông qua quét WN-list 
và thuật toán giao hai WN-list chỉ có độ phức tạp tuyến tính. Các thực nghiệm trên nhiều loại CSDL đã cho thấy NFWI 
hoạt động hiệu quả hơn các thuật toán khai thác FWI hiện có. 
Trong tương lai, chúng tôi sẽ tập trung vào việc áp dụng cấu trúc N-list trong một số bài toán khai thác dữ liệu 
khác như khai thác tập phổ biến tiện ích cao hay khai thác tập phổ biến trên CSDL tăng trưởng. 
0
50
100
150
4 2 1 0.4 0.2 0.1
Ti
m
e
(s
) 
minws(%) 
a 
WIT-FWIs-Diff IWS
0
20
40
60
80
4 2 1 0.4 0.2 0.1
Ti
m
e
(s
) 
minws(%) 
b 
NFWI IWS
0
1000
2000
3000
0.8 0.4 0.2 0.08 0.04 0.02
Ti
m
e
(s
) 
minws(%) 
a 
WIT-FWIs-Diff IWS
0
200
400
600
800
0.8 0.4 0.2 0.08 0.04 0.02
Ti
m
e
(s
) 
minws(%) 
b 
NFWI IWS
254 KHAI THÁC TẬP PHỔ BIẾN CÓ TRỌNG SỐ DỰA TRÊN CẤU TRÚC N-LIST 
TÀI LIỆU THAM KHẢO 
[1] R. Agrawal, T. Imielinski, and A. Swami, "Mining association rules between sets of items in large databases," in SIGMOD '93 
Proceedings of the 1993 ACM SIGMOD international conference on Management of data, 1993, pp. 207-216. 
[2] R. Agrawal, H. Mannila, R. Srikant, H. Toivonen, and I. A. Verkamo, "Fast discovery of association rules," in Advances in 
knowledge discovery and data mining. American Association for Artificial Intelligence Menlo Park, 1996, pp. 307-328. 
[3] J. Han, J. Pei, and Y. Yin, "Mining frequent patterns without candidate generation," in SIGMOD '00 Proceedings of the 2000 
ACM SIGMOD international conference on Management of data, 2000, pp. 1-12. 
[4] G. Grahne and J. Zhu, "Fast algorithms for frequent itemset mining using FP-trees," IEEE Transactions on Knowledge and 
Data Engineering, vol. 17, no. 10, pp. 1347-1362, 2005. 
[5] M. J. Zaki, "Scalable algorithms for association mining," IEEE Transactions on Knowledge and Data Engineering, vol. 12, no. 
3, pp. 372-390, 2000. 
[6] M. J. Zaki and K. Gouda, "Fast vertical mining using diffsets," in KDD '03 Proceedings of the ninth ACM SIGKDD 
international conference on Knowledge discovery and data mining, 2003, pp. 326-335. 
[7] B. Vo, L. Hong, and B. Le, "DBV-Miner: A Dynamic Bit-Vector approach for fast mining frequent closed itemsets," Expert 
Systems with Applications, vol. 39, no. 8, pp. 7196-7206, 2012. 
[8] Z. Deng, Z. Wang, and J. Jiang, "A new algorithm for fast mining frequent itemsets using N-lists," Science China Information 
Sciences, vol. 55, no. 9, pp. 2008-2030, 2012. 
[9] B. Vo, T. Le, F. Coenen, and T.-P. Hong, "Mining frequent itemsets using the N-list and subsume concepts," International 
Journal of Machine Learning and Cybernetics, pp. 1-13, 2014. 
[10] Z. Deng and S. Lv, "PrePost+: An efficient N-list-based algorithm for mining frequent itemsets via Children-Parent 
Equivalence pruning," Expert Systems with Applications, vol. 42, no. 13, pp. 5424-5432, 2015. 
[11] G. D. Ramkumar, S. Ranka, and S. Tsur, "Weighted Association Rules: Model and Algorithm," in Proc. Fourth ACM Int’l 
Conf. Knowledge Discovery and Data Mining, 1998, pp. 01-13 
[12] C. H. Cai, A. W. C. Fu, C. H. Cheng, and W. W. Kwong, "Mining association rules with weighted items," in Database 
Engineering and Applications Symposium, 1998. Proceedings. IDEAS'98. International, 1998, pp. 68-77. 
[13] F. Tao, F. Murtagh, and M. Farid, "Weighted Association Rule Mining Using Weighted Support and Significance Framework," 
in KDD '03 Proceedings of the ninth ACM SIGKDD international conference on Knowledge discovery and data mining, 2003, 
pp. 661-666. 
[14] B. Vo, F. Coenen, and B. Le, "A new method for mining Frequent Weighted Itemsets based on WIT-trees," Expert Systems 
with Applications, vol. 40, no. 4, pp. 1256-1264, 2013. 
[15] H. D. Nguyen, B. Vo, M. H. T. Nguyen, and T.-P. Hong, "An Improved Algorithm for Mining Frequent Weighted Itemsets," in 
Systems, Man, and Cybernetics (SMC), 2015 IEEE International Conference on, 2015, pp. 2579-2584. 
[16] R. Rymon, "Search through systematic set enumeration," in In Proc. Int'l Conf. principles of knowledge representation and 
reasoning, 1992, pp. 539-550. 
A WEIGHTED N-LIST-BASED METHOD FOR MINING FREQUENT 
WEIGHTED ITEMSETS 
Bui Danh Huong, Vo Dinh Bay, Nguyen Duy Ham 
ABSTRACT— Mining frequent itemsets plays an important role in data mining. There have been many different methods proposed 
to solve this problem. In particular, the N-list structure proposed by Deng et al. (Deng, Wang, & Jiang, 2012) that use a hybrid 
approach between the FP-tree and enumerate-tree achieved encouraging efficiency. However, this method operates only on binary 
databases. In this paper, we proposed the WN-list (Weighted N-list) structure, an extension of the N-list structure, to solve the 
problem of mining frequent weighted itemsets from weighted database. First, some theorems are developed to calculate the weight 
support of an itemset, and then, an algorithm is built based on these theorems for fast mining frequent weighted itemsets. 
Experimental results on a variety of databases (sparse and dense) show that the proposed method outperforms existing methods, 
especially with the small threshold.