Giáo trình Xử lý tín hiệu số
TÍN HIỆU, HỆ THỐNG và XỬ LÝ TÍN HIỆU
Để hiểu “Xử lý tín hiệu” là gì, ta sẽ tìm hiểu ý nghĩa của từng từ. Tín hiệu(signal) dùng để
chỉ một đại lượng vật lý mang tin tức. Về mặt toán học, ta có thể mô tả tín hiệu như là một
hàm theo biến thời gian, không gian hay các biến độc lập khác. Chẳng hạn như, hàm:
x( ) 20 t t = 2 mô tả tín hiệu biến thiên theo biến thời gian t. Hay một ví dụ khác, hàm:
s( , ) 3 5 x y x xy y = + + 2 mô tả tín hiệu là hàm theo hai biến độc lập x và y, trong đó x và y
biểu diễn cho hai tọa độ không gian trong mặt phẳng.
Hai tín hiệu trong ví dụ trên thuộc về lớp tín hiệu có thể được biểu diễn chính xác bằng hàm
theo biến độc lập. Tuy nhiên, trong thực tế, các mối quan hệ giữa các đại lượng vật lý và các
biến độc lập thường rất phức tạp nên không thể biểu diễn tín hiệu như trong hai ví dụ vừa nêu
trên.
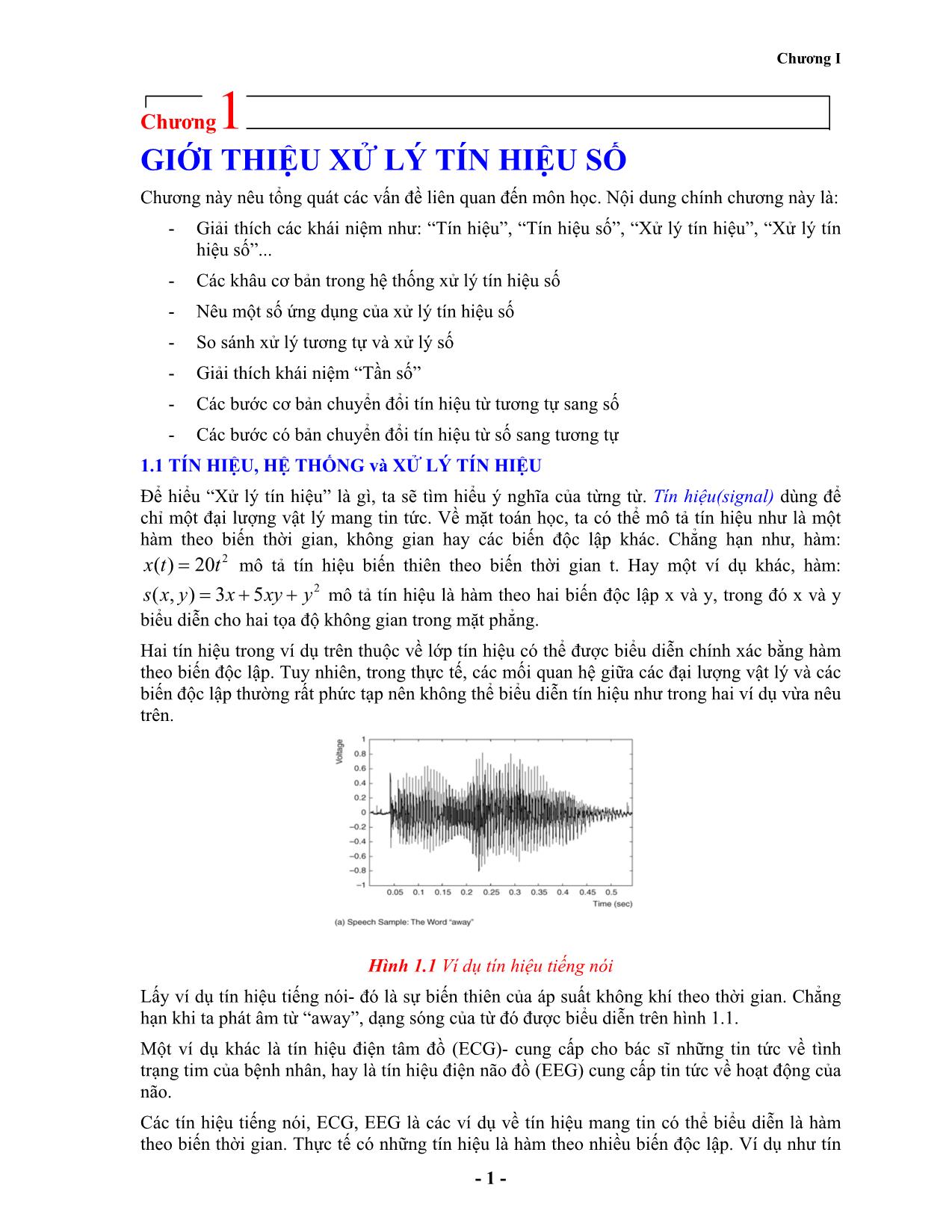
Hình 1.1 Ví dụ tín hiệu tiếng nói
Lấy ví dụ tín hiệu tiếng nói- đó là sự biến thiên của áp suất không khí theo thời gian. Chẳng
hạn khi ta phát âm từ “away”, dạng sóng của từ đó được biểu diễn trên hình 1.1.
Một ví dụ khác là tín hiệu điện tâm đồ (ECG)- cung cấp cho bác sĩ những tin tức về tình
trạng tim của bệnh nhân, hay là tín hiệu điện não đồ (EEG) cung cấp tin tức về hoạt động của
não.
Các tín hiệu tiếng nói, ECG, EEG là các ví dụ về tín hiệu mang tin có thể biểu diễn là hàm
theo biến thời gian. Thực tế có những tín hiệu là hàm theo nhiều biến độc lập. Ví dụ như tínChương I
hiệu ảnh (image)- là sự thay đổi của cường độ ánh sáng theo không gian, có thể xem là hàm
độ sáng theo hai biến không gian.
Tất cả các tín hiệu đều do một nguồn nào đó tạo ra, theo một cách thức nào đó. Ví dụ tín hiệu
tiếng nói được tạo ra bằng cách ép không khí đi qua dây thanh âm. Một bức ảnh có được
bằng cách phơi sáng một tấm phim chụp một cảnh/ đối tượng nào đó. Quá trình tạo ra tín
hiệu như vậy thường liên quan đến một hệ thống, hệ thống này đáp ứng lại một kích thích
nào đó. Trong tín hiệu tiếng nói, hệ thống là hệ thống phát âm, gồm môi, răng, lưỡi, dây
thanh. Kích thích liên quan đến hệ thống được gọi là nguồn tín hiệu (signal source). Như
vậy ta có nguồn tiếng nói, nguồn ảnh và các nguồn tín hiệu khác.

Trang 1

Trang 2
Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Giáo trình Xử lý tín hiệu số

ủa DFT là hữu hạn: Chương V - 96 - 2 2 0 1 0 1 1 0 1 0 2[ ] ( ) 0 1 1 [ ] [ ] 01 1 k N kn N N j n k N n N j n kX k X k N N x n e x n e k N π π π − − Ω Ω= , = , , , − = − − = = Ω |Ω = , = , , , − = | = , = , , , − ∑ ∑ L L L Để cho gọn, ta ký hiệu: N 2j N eW π−= Khi không cần để ý đến N, ta có thể viết đơn giản W thay cho NW Vậy, 1 0 [ ] [ ] 0 1 1 N kn N n X k x n W k N − = = , = , , , −∑ L là DFT của dãy 0[ ]x n . lấy cửa sổ từ x[n] Ví dụ: Tính DFT của ]Nn[u]n[u]n[x −−= 21 1 0 0 ( ) j k N N N n kn n n e W π−− − = = =∑ ∑ Suy ra DFT của [ ] 1 0 1 7x n n= , = , , , .L Ví dụ: Cho 1 0 [ ] 0 1 7 n x n n , =⎧= ⎨ , = , ,⎩ . Tìm [ ] 0 1 7X k k , = , , , Chương V - 97 - Chương V - 98 - Ví dụ: Cho [ ] [ 2]y n nδ= − và 8N = . Tìm [ ]Y k Ví dụ: Cho [ ] 0 1 1pnNx n cW n N −= , = , , , − , với p là một số nguyên [0 1 1]p N∈ , , , − và 2NjNW e π−= Tìm DFT của [ ]x n . 5.2.2 Biểu thức tính biến đổi Fourier rời rạc ngược Trong mục này, ta sẽ đi thiết lập công thức khôi phục [ ]x n từ [ ]X k . Sự khôi phục này được gọi là tổng hợp hay DFT ngược (IDFT) Từ biểu thức tính DTFT ngược được thiết lập trong mục 5.2.1 và do tính tương hỗ giữa miền thời gian và tần số, ta có thể suy ra biểu thức tính IDFT như sau: 1 0 1[ ] [ ] 0 1 1 N kn N k x n X k W n N N − − = = , = , , , −∑ Chương V - 99 - Sau đây ta sẽ chứng minh điều này đúng: 1 1 0 0 1 1 ( ) 0 0 1[ ] [ ] 1 [ ] N N kl kn N N k l N N k l n N l k x n x l W W N x l W N − − − = = − − − = = = = ∑∑ ∑ ∑ Ta có 1 ( ) 0 0 N k l n N k N l n W l n − − = , =⎧= ⎨ , ≠⎩∑ Thay kết quả này vào x[n] ta có được biểu thức tính IDFT trên là đúng 1 1 1 ( ) 0 0 0 1 1[ ] [ ] [ ] [ ] 1 ( [ ]) [ ] N N N k l n N l k l x n x l W x l N n l N N Nx n x n N δ− − −− = = = = = − = = ∑ ∑ ∑ Ví dụ: Tìm IDFT của [ ] 1 0 1 7X k k = , = , , , . Ví dụ: Cho [ ] [ ] 2 [ 1] 3 [ 2] [ 3]x n n n n nδ δ δ δ= + − + − + − và 4N = , tìm [ ]X k . Chương V - 100 - Ví dụ: Cho [ ] 2 [ ] 2 [ 2]X k k kδ δ= + − và 4N = , tìm [ ]x n . 5.2.3 Chọn số mẫu tần số N Qua mục 5.2.1 ta thấy biểu thức tính DFT được thành lập từ việc lấy mẫu DTFT với số mẫu là N. Số mẫu N này cũng chính là số mẫu của tín hiệu rời rạc trong miền thời gian hay là độ dài của cửa sổ DFT, nói ngắn gọn là số mẫu tần số bằng số mẫu thời gian. Ví dụ: Cho tín hiệu x[n] như hình bên. Tính rồi vẽ hai loại phổ biên độ |)(X| Ω và |X[k]| trên đồ thị. Xem đồ thị ta thấy rõ ràng rằng: các mẫu |X[k]| bằng với |)(X| Ω tại cùng tần số. Chương V - 101 - Việc chọn N ảnh hưởng đến độ phân giải của phổ rời rạc. Chọn N càng lớn, độ phân giải càng tốt, nghĩa là khoảng cách giữa hai vạch phổ cạnh nhau X[k] và X[k+1] càng nhỏ, nghĩa là đường bao của phổ rời rạc X[k] càng gần với hình ảnh của phổ liên tục |)(X| Ω . Để việc tăng N không làm ảnh hưởng đến kết quả, ta kéo dài tín hiệu trong miền thời gian ra bằng cách chèn thêm các mẫu bằng 0 (zero-padding) vào phía cuối của tín hiệu. Ví dụ: Cho [ ] [ ] [ 5]x n u n u n= − − . Tìm X[k] với N như sau: (a) N = 5. Chương V - 102 - (b) N = 10 5.2.4 Các tính chất của biến đổi Fourier rời rạc Hầu hết các tính chất của DFT tương tự như các tính chất của DTFT, nhưng có vài điểm khác nhau. Điểm khác nhau đó là do DFT chính là một chu kỳ trích ra từ dãy DFS tuần hoàn với chu kỳ N. Bây giờ ta thay đổi ký hiệu, ký hiệu [ ]x n% là dãy tuần hoàn chu kỳ N, [ ]x n là một chu kỳ trích ra từ [ ]x n% : [ ] [ ] [ ] k x n x n n kNδ∞ =−∞ = ∗ −∑% = ∑∞ −∞= − k ]kNn[x Chương V - 103 - 1. Dịch vòng Nếu [ ] [ ] DFT x n X k↔ thì ]k[XW]mn[x km DFT↔− với 2NjNW e π−= Ví dụ: Dịch vòng đi m mẫu sẽ cho kết quả trùng với dich vòng đi (m mod N) mẫu. 2. Tổng chập vòng , 1 2 1 2[ ] [ ] [ ] [ ] DFT N x n x n X k X k⊗ ↔ ở đây: 1 1 2 1 2 mod 0 [ ] [ ] [ ] [ ] [ ] N N p y n x n x n x p x n p − = = ⊗ = −∑ Dấu ⊗ là ký hiệu tổng chập vòng. Nhắc lại công thức tổng chập tuyến tính: 1 2 1 2[ ] [ ] [ ] [ ] [ ] p y n x n x n x p x n p ∞ =−∞ = ∗ = −∑ Chương V - 104 - Thoạt nhìn, ta thấy biểu thức tính tổng chập vòng rất giống tổng chập tuyến tính. Tuy nhiên, hai phép chập đó khác nhau ở những điểm sau đây: - Phép chập vòng chỉ áp dụng cho hai dãy dài hữu hạn và bằng nhau, kết quả cũng là một dãy cùng chiều dài, nghĩa là 1[ ]x n , 2[ ]x n , and [ ]y n đều có chiều dài là N. Trong khi đó, phép chập tuyến tính áp dụng cho hai dãy có chiều dài bất kỳ: nếu 1[ ]x n dài 1x N , 2[ ]x n dài 1xN thì [ ]y n dài - Phép dịch trong tổng chập vòng là phép dịch vòng, khác với phép dịch trong tổng chập tuyến tính là phép dịch tuyến tính. Vì những điểm khác nhau trên nên kết quả của tổng chập vòng và tổng chập tuyến tính của cùng hai dãy có thể không trùng nhau. Tuy nhiên, ta có cách làm cho hai kết quả đó trùng nhau như sau: - Chuyển tổng chập tuyến tính sang miền tần số: )(X).(X)(Y 21 ΩΩ=Ω - Lấy mẫu )(Y Ω với số mẫu là 1NNNN 21 xxy −+=≥ , ta được: ]k[H].k[X]k[Y = - Tính DFT ngược, ta được: y[n] = x[n] * h[n] ở đây chiều dài của y[n] , x[n] và h[n] là: 1NNNN 21 xxy −+=≥ Như vậy, bằng cách kéo dài các tín hiệu x1[n] và x2[n] ra đến chiều dài 1NNNN 21 xxy −+=≥ rồi lấy chập vòng, ta được hai kết quả của tổng chập vòng và chập tuyến tính là trùng nhau: ]n[x]n[x]n[x]n[x]n[y 2121 ⊗=∗= Ví dụ: Tìm 1 2[ ] [ ] [ ]x n x n z n⊗ = , với 1[ ] [1,2,0,0]x n = , 2[ ] [1,1,0,0]x n = và N = 4. Kết quả này có trùng với tổng chập tuyến tính không? Chương V - 105 - Ví dụ: Tìm [ ] [ ] [ ]y n x n x n= ⊗ , với [ ] [1,0,1,1]x n = trong hai trường hợp: (a) N = 4 (b) N = 8 N bằng bao nhiêu là đủ để tổng chập vòng trùng với tổng chập tuyến tính? 5.3 MỘT SỐ ỨNG DỤNG CỦA DFT Phần này sẽ giới thiệu sơ lược về một số ứng dụng của DFT trong thực tế 5.3.1 Phân tích phổ tín hiệu Trong chương trước, ta đã biết được ý nghĩa của phổ trong việc phân tích tín hiệu, từ phổ của tín hiệu ta biết được một số thông tin cần thiết. Để tìm phổ của tín hiệu (cả liên tục và rời rạc), ta cần phải biết giá trị của tín hiệu tại tất cả các thời điểm. Tuy nhiên trong thực tế, do ta chỉ quan sát được tín hiệu trong một khoảng thời gian hữu hạn nên phổ tính được chỉ là xấp xỉ của phổ chính xác. DFT được ứng dụng rất hiệu quả trong việc tính toán phổ xấp xỉ này. Trong thực tế, nếu tín hiệu cần phân tích là tín hiệu liên tục, trước hết ta cho tín hiệu đó đi qua một bộ lọc chống chồng phổ rồi lấy mẫu với tần số B2Fs ≥ , với B là băng thông của tín hiệu sau khi lọc. Như vậy, tần số cao nhất chứa trong tín hiệu rời rạc là Fs/2. Sau đó, ta phải giới hạn chiều dài của tín hiệu trong khoảng thời gian T0 = LT, với L là số mẫu và T là khoảng cách giữa hai mẫu. Cuối cùng, ta tính DFT của tín hiệu rời rạc L mẫu. Như đã trình bày trên, muốn tăng độ phân giải của phổ rời rạc, ta tăng chiều dài của DFT bằng cách bù thêm số 0 vào cuối tín hiệu rời rạc trước khi tính DFT. Ví dụ sau đây minh họa một ứng dụng của DFT trong việc phân tích phổ tín hiệu điện tâm đồ (ECG): Hình vẽ (a) là đồ thị của 11 nhịp tim của một bệnh nhân. 11 nhịp tim này xuất hiện trong khoảng thời gian 9 giây, tương đương với 11/9 = 1.22 nhịp trong một giây, hay 73 nhịp trong một phút. Hình (b) là chi tiết nửa đầu của nhịp tim thứ tư. Hình (c) là một đoạn phổ biên độ DFT có được sau khi lấy mẫu đoạn 11 nhịp tim (a) với tần số lấy mẫu là 8 kHz. Nhìn (c) ta thấy có hai điểm biên độ cao nhất xuất hiện ở tần số 88 Hz Chương V - 106 - và 235 Hz. Để tìm hiểu phổ kỹ hơn, ta tính DFT của tín hiệu ở hình (b)- phổ này thể hiện ở hình (d), ở đây ta thấy rõ hai điểm biên độ cao nhất ở tần số 88 Hz và 235 Hz bên trong mỗi nhịp tim. Tuy nhiên, ta không thấy tần số lặp lại nhịp tim là 1.22 Hz trong DFT hình (c). Hình (e) giải thích rõ hơn điều này. Nó là phiên bản mở rộng của các đỉnh nhọn trong dải tần từ 60 Hz đến 100 Hz. Trong khi tần số 1.22 Hz quá nhỏ nên không thấy rõ trong hình (c) thì trong hình (e) này, ta thấy rõ các hài của tần số 1.22 Hz và thấy rõ khoảng cách giữa hai đỉnh nhọn là 1.22 Hz. 5.3.2 Tính tín hiệu ra hệ thống rời rạc LTI Tín hiệu ra hệ thống rời rạc LTI được tính bằng cách chập tín hiệu vào với đáp ứng xung của hệ thống: ]n[h]n[x]n[y ∗= Ta có hai cách để tính tổng chập này: một là tính trực tiếp, hai là tính thông qua tổng chập vòng như phân tích trong mục 5.2.4. Cách tính qua tổng chập vòng sẽ có lợi hơn về mặt thời gian. Lý do là tổng chập vòng có thể tính thông qua DFT, mà DFT có thể được tính nhanh nhờ thuật toán tính nhanh FFT. Để tính y[n], ta thực hiện theo các bước sau đây: - Kéo dài x[n] đến độ dài N = Nx + Nh - 1 Chương V - 107 - - Kéo dài h[n] đến độ dài N = Nx + Nh - 1 - Tính DFT của x[n] N mẫu, ta được X[k] - Tính DFT của h[n] N mẫu, ta được H[k] - Nhân X[k] với H[k], ta được Y[k]: Y[k] = X[k].H[k] - Tính DFT ngược của Y[k], ta được y[n] Việc tính DFT và DFT ngược được thực hiện nhờ một thuật toán tính nhanh DFT, gọi là FFT (Fast Fourier Transform). Phần sau sẽ trình bày về thuật toán FFT. 5.4 TÍNH NHANH DFT BẰNG THUẬT TOÁN FFT DFT được ứng dụng rộng rãi trong xử lý tín hiệu rời rạc/ số nên nhiều nhà toán học, kỹ sư đã rất quan tâm đến việc rút ngắn thời gian tính toán. Năm 1965, Cooley và Tukey đã tìm ra thuật toán tính DFT một cách hiệu quả gọi là thuật toán FFT. Cần lưu ý FFT không phải là một phép biến đổi mà là một thuật toán tính DFT nhanh và gọn hơn. Để đánh giá hiệu quả của thuật toán, ta sử dụng số phép tính nhân và cộng phức. Số phép nhân và cộng phức liên quan trực tiếp đến tốc độ tính toán khi thuật toán được thực hiện trên các máy tính hay là các bộ xử lý chuyên dụng. 5.4.1 Hiệu quả tính toán của FFT Công thức tính DFT của dãy dài N: 1 0 [ ] [ ] N kn n X k x n W − = =∑ Qua đây ta thấy để tính mỗi giá trị DFT ta cần N phép nhân và cộng phức. Để tính toàn bộ DFT ta cần 2N phép nhân và cộng phức. Tuy nhiên, nếu tính DFT nhờ thuật toán FFT thì số phép nhân và cộng phức giảm xuống chỉ còn 22 logN N . Ví dụ như 102 1024N = = thì nếu tính trực tiếp DFT cần 2 20 62 10N = = phép nhân và cộng phức, trong khi tính qua FFT thì số phép nhân và cộng phức giảm xuống chỉ còn 22 logN N = 5120. Số phép tính giảm đi gần 200 lần! Hình sau cho thấy rõ hiệu quả của thuật toán FFT: 0 20 40 60 80 100 0 2000 4000 6000 8000 10000 N, Size of DFT or FFT N um ber of O perations Chương V - 108 - Có nhiều thuật toán FFT khác nhau bao gồm FFT phân chia theo thời gian và FFT phân chia theo tần số. Trong phần này ta tập trung vào thuật toán FFT cơ số 2 ( 2 where is an integeriN i= ) phân chia theo thời gian. 5.4.2 Nguyên tắc của FFT Nguyên tắc cơ bản mà các thuật toán FFT đều dựa vào là phân chia DFT N mẫu thành các DFT nhỏ hơn một cách liên tục: Với N = 2i, đầu tiên ta phân chia DFT N mẫu thành các DFT 2N mẫu, sau đó phân chia DFT 2 N mẫu thành DFT 4N mẫu và cứ tiếp tục như thế cho đến khi được các DFT dài N = 2. Việc tính DFT nhỏ hơn rõ ràng sẽ cần ít phép tính nhân và cộng phức hơn. Trước tiên, chia [ ]x n thành các dãy con chẵn và lẻ: even odd [ ] [ ] [ ]kn kn n n X k x n W x n W= +∑ ∑ Đặt 2n m= với n chẵn và 2 1n m= + với n lẻ: 2 21 1 2 (2 1) 0 0 [ ] [2 ] [2 1] N N mk k m m m X k x m W x m W − − + = = = + + =∑ ∑ 2 21 1 2 2 0 0 [2 ]( ) [2 1]( ) N N mk k mk m m x m W W x m W − − = = + + =∑ ∑ [ ] [ ] [ ] [ ] [ ]k ke oX k X k W X k G k W H k= + = + [ ]eX k và [ ]oX k là DFT 2N mẫu. Tiếp theo chia dãy con 2N mẫu là x[2m] làm đôi bằng cách đặt 2m p= : 4 41 1 4 2 4 0 0 [ ] [4 ]( ) [4 2]( ) N N kp k kp e p p X k x p W W x p W − − = = = + + =∑ ∑ Thực hiện tương tự như vậy cho dãy con x[2m+1] Ví dụ: N = 8 Quá trình phân chia DFT 8 mẫu thành các DFT nhỏ hơn được minh họa trên lưu đồ. Đầu tiên, chia x[n] thành 2 dãy con, dãy thứ nhất là dãy chẵn x[0], x[2], x[4], x[6] và dãy thứ hai là dãy lẻ x[1], x[3], x[5], x[7]. Tiếp theo, chia dãy chẵn thành 2 dãy con, dãy thứ nhất là x[0], x[4] và dãy thứ hai là x[2], x[6]. Tương tự, dãy lẻ được chia thành 2 dãy con, là dãy x[1], x[5] và dãy x[3], x[7]. Các DFT 2 mẫu được tính đơn giản như sau: ]1[g]0[gW]1[gW]0[g]1[G ]1[g]0[gW]1[gW]0[g]0[G 1eW,1k0,W]n[g]k[G 1.11.0 0.10.0 2 2j1 0n nk −=+= +=+=⇒ −==≤≤= π− = ∑ (chỉ cần phép cộng và trừ) Chương V - 109 - Chương V - 110 - FFT cơ sở: A “Butterfly” 0 WNr WN(r + N/2) Lưu ý: WN(r + N/2) = WN N/2 WNr = -1 WNr = - WNr , do đó có thể vẽ lại lưu đồ FFT đơn giản như sau: Chương V - 111 - Phụ lục 1 Summary: The Common Types of Fourier Transforms Continuous in Time ( )x t = Aperiodic in Frequency Discrete in Time [ ]x n = Periodic in Frequency Periodic in Time, = Discrete in Frequency Fourier Series (FS): 0 1 ( ) jk tk Ta x t e dtT ω−= ∫ 0( ) jk tk k x t a e ω ∞ =−∞ = ∑ Discrete Fourier Series (DFS) and Discrete Fourier Transform (DFT): 1 0 [ ] [ ] ,0 1 N kn N n X k x n W k N − = = ≤ ≤ −∑ 1 0 1[ ] [ ] ,0 1 N kn N k x n X k W n N N − − = = ≤ ≤ −∑ where 2 Nj NW e π−= . Aperiodic in Time, = Continuous in Frequency Fourier Transform (FT): ( ) ( ) ( ) ( ) j t j t X x t e dt x t X e dt ω ω ω ω ∞ − −∞ ∞ − −∞ = = ∫ ∫ Discrete-Time Fourier Transform (DTFT): ( ) [ ] j n n X x n e ∞ − Ω =−∞ Ω = ∑ 2 1[ ] ( ) 2 j nx n X e dππ Ω= Ω Ω∫ Chương V - 112 - Phụ lục 2 Some Fourier Relationships The Fourier transform is the Laplace transform evaluated on the j∞ axis. ( ) ( ) ( ) ( )j t st s j s j X x t e dt X s x t e dtω ω ω ω ∞ ∞− −=−∞ −∞ = ⎡ ⎤= = = ⎢ ⎥⎣ ⎦∫ ∫ The discrete-time Fourier transform is the z-transform evaluated around the unit circle. ( ) [ ] ( ) [ ]j j j n n z e n n z e X x n e X z x n xΩ Ω ∞ ∞− Ω − ==−∞ =−∞ = ⎡ ⎤Ω = = = ⎢ ⎥⎣ ⎦∑ ∑ Discrete-time periodic signals can also be described by a Fourier Series expansion: 0[ ] synthesis equationjk nk k N x n a e Ω ∈ = ∑ and 0 1 [ ] analysis equationjk nk n N a x n e N − Ω ∈ = ∑ then using the DTFT of the impulse train, ( )P Ω that we previously found, the DTFT of an arbitrary discrete-time periodic signal can be found from 0 ( )X Ω the DTFT of one period 0[ ]x n 0 2 2( ) ( ) ( ) k kX X N N π πδ⎛ ⎞Ω = Ω Ω−⎜ ⎟⎝ ⎠∑ 0 2 2 2( ) ( ) k k kX N N N π π πδ= Ω−∑ The DFT is simply a scaled version of the terms of one period of the discrete time Fourier transform for a periodic sequence: 1 0 0 2[ ] ( ) [ ] ,0 1 N kn N n kX k X x n W k N N π − = = = ≤ ≤ −∑ for 2 0 1 1kN k NπΩ = , = , , , − , i.e. only look at the N distinct sampled frequencies of 0 ( )X Ω . Also important, the orthogonality of exponentials: 1 0 [ ] N kn N n W N kδ− = =∑ where 2 Nj NW e π−= .
File đính kèm:
 giao_trinh_xu_ly_tin_hieu_so.pdf
giao_trinh_xu_ly_tin_hieu_so.pdf

