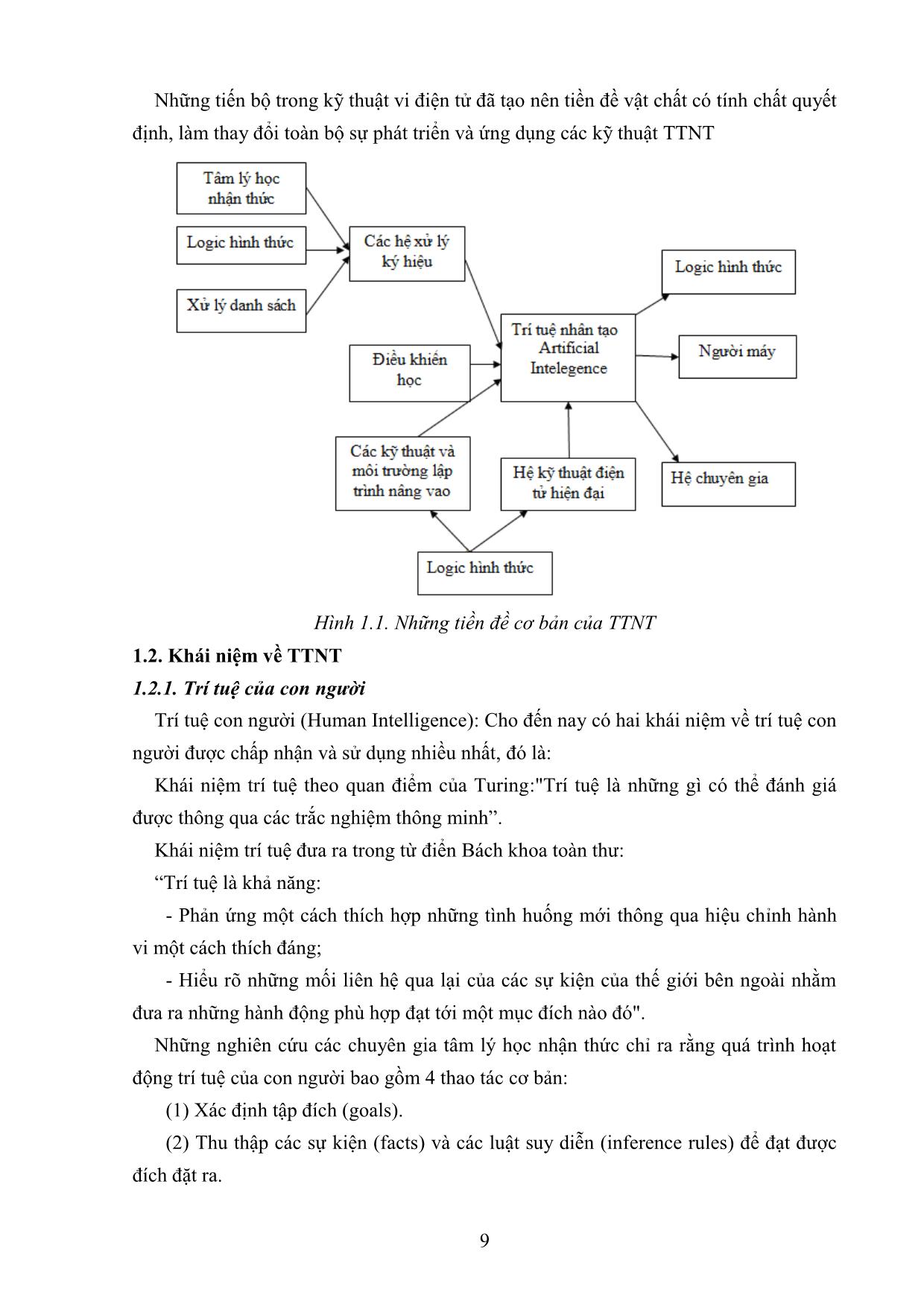
Giáo trình Nhập môn trí tuệ nhân tạo (Phần 1)

hức G  H đã đƣợc chứng minh. 
 105 
 Trong các hệ tri thức, chẳng hạn các hệ chuyên gia, hệ lập trình logic,..., sử dụng 
các luật suy diễn ngƣời ta thiết kế lên các thủ tục suy diễn (còn đƣợc gọi là thủ tục 
chứng minh) để từ các tri thức trong CSTT ta suy ra các tri thức mới đáp ứng nhu cầu 
của ngƣời sử dụng. 
 Một hệ hình thức (formal system) bao gồm một tập các tiên đề và một tập các luật 
suy diễn nào đó (trong ngôn ngữ biểu diễn tri thức nào đó). 
 Một tập luật suy diễn đƣợc xem là đầy đủ, nếu mọi hệ quả logic của một tập các tiên 
đề đều chứng minh đƣợc bằng cách chỉ sử dụng các luật của tập đó. 
Phương pháp chứng minh bác bỏ 
Phƣơng pháp chứng minh bác bỏ (refutation proof hoặc proof by contradiction) là 
một phƣơng pháp thƣờng xuyên đƣợc sử dụng trong các chứng minh toán học. Tƣ 
tƣởng của phƣơng pháp này là nhƣ sau Để chứng minh P đúng, ta giả sử P sai (thêm 
 P vào các giả thiết) và dẫn tới một mâu thuẫn. 
Giả sử chúng ta có một tập hợp các công thức G ={G1,..., Gm} ta cần chứng minh 
công thức H là hệ quả logic của G Điều đó tƣơng đƣơng với chứng minh công thức 
G1...Gm H là vững chắc. Thay cho chứng minh G1... Gm H là vững chắc, ta 
chứng minh G1...Gm  H là không thỏa mãn đƣợc. Tức là ta chứng minh tập G‟= 
(G1,..., Gm, H) là không thỏa đƣợc nếu từ G‟ ta suy ra hai mệnh đề đối lập nhau. Việc 
chứng minh công thức H là hệ quả logic của tập các tiêu đề G bằng cách chứng minh 
tính không thỏa đƣợc của tập các tiêu đề đƣợc thêm vào phủ định của công thức cần 
chứng minh, đƣợc gọi là chứng minh bác bỏ. 
3.4. Luật phân giải. Thủ tục chứng minh bác bỏ bằng luật phân giải 
 Để thuận tiện cho việc sử dụng luật giải, chúng ta sẽ cụ thể hoá luật giải trên các 
dạng câu đặc biệt quan trọng. 
Luật giải trên các câu tuyển: 
A1 .... Am C 
 CB1 .....Bn 
A1 ....AmB1 ...Bn 
trong đó Ai, Bj và C là các literal. 
Luật giải trên các câu Horn: 
 Giả sử Pi (1 i m), Rj (1 j n), Q và S là các literal. Khi đó ta có các luật sau 
P1 ....Pm  S Q, 
R1 .... Rn S 
P1 ...Pm  R1 ...  Rn Q 
 106 
Một trƣờng hợp riêng hay đƣợc sử dụng của luật trên là 
P1 ... Pm  S Q, 
              S 
P1 ...Pm Q 
Khi ta có thể áp dụng luật giải cho hai câu, thì hai câu này đƣợc gọi là hai câu giải 
được và kết quả nhận đƣợc khi áp dụng luật giải cho hai câu đó đƣợc gọi là giải thức 
của chúng. Giải thức của hai câu A và B đƣợc kí hiệu là res(A, B). Chẳng hạn, hai câu 
tuyển giải đƣợc nếu một câu chứa một literal đối lập với một literal trong câu kia. Giải 
thức của hai literal đối lập nhau (P và P) là câu rỗng. 
Ký hiệu câu rỗng là [] (hoặc ), câu rỗng không thoả đƣợc. 
Giả sử G là một tập các câu tuyển (Bằng cách chuẩn hoá ta có thể đƣa một tập các 
công thức về một tập các câu tuyển). Ký hiệu R(G) là tập câu bao gồm các câu thuộc 
G và tất cả các câu nhận đƣợc từ G bằng một dãy áp dụng luật phân giải. 
Luật phân giải là luật đầy đủ để chứng minh một tập câu là không thỏa đƣợc. Điều 
này đƣợc suy từ định lý sau 
Định lý phân giải: 
Một tập câu tuyển là không thỏa đƣợc nếu và chỉ nếu câu rỗng [] R(G). 
Định lý phân giải có nghĩa rằng, nếu từ các câu thuộc G, bằng cách áp dụng luật 
phân giải ta dẫn tới câu rỗng thì G là không thỏa đƣợc, còn nếu không thể sinh ra câu 
rỗng bằng luật giải thì G thỏa đƣợc. Lƣu ý rằng, việc dẫn tới câu rỗng có nghĩa là ta đã 
dẫn tới hai literal đối lập nhau P và P (tức là dẫn tới mâu thuẫn). 
Từ định lý phân giải, ta đƣa ra thủ tục sau đây để xác định một tập câu tuyển G là 
thỏa đƣợc hay không Thủ tục này đƣợc gọi là thủ tục phân giải. 
Input Tập G các câu tuyển 
Output: Kết luận G thỏa đƣợc hay không thỏa đƣợc. 
Procedure Resolution; 
Begin 
1. Repeat 
1.1. Chọn hai câu A và B thuộc G; 
1.2. if A và B phân giải đƣợc then tính Res (A, B) ; 
1.3. if Res (A, B) là câu mới then thêm Res (A, B) vào G; 
until 
nhận đƣợc [] hoặc không có câu mới xuất hiện; 
2. if nhận đƣợc câu rỗng then thông báo G không thoả đƣợc 
 107 
else thông báo G thoả đƣợc; 
End; 
 Nhận xét: nếu G là tập hữu hạn các câu thì các literal có mặt trong các câu của G là 
hữu hạn. Do đó số các câu tuyển thành lập đƣợc từ các literal đó là hữu hạn. Vì vậy chỉ 
có một số hữu hạn câu đƣợc sinh ra bằng luật phân giải. Thủ tục phân giải sẽ dừng lại 
sau một số hữu hạn bƣớc. 
Chỉ sử dụng luật phân giải ta không thể suy ra mọi công thức là hệ quả logic của 
một tập công thức đã cho. Tuy nhiên, sử dụng luật phân giải ta có thể chứng minh 
đƣợc một công thức bất kì có là hệ quả của một tập công thức đã cho hay không bằng 
phƣơng pháp chứng minh bác bỏ. Vì vậy luật giải đƣợc xem là luật đầy đủ cho bác bỏ. 
Sau đây là thủ tục chứng minh bác bỏ bằng luật giải: 
input Tập G các công thức; 
Công thức cần chứng minh H; 
Output: Kết luận H đƣợc chứng minh. 
Procedure Refutation_Proof 
 Begin 
1. Thêm H vào G; 
2. Chuyển các công thức trong G về dạng chuẩn hội; 
3. Từ các dạng chuẩn hội ở bƣớc hai, thành lập tạp các câu tuyển G‟; 
4. Áp dụng thủ tục giải cho tập câu G‟; 
5. if G‟ không thoả đƣợc then thông báo H là hệ quả logic; 
 else thông báo H không là hệ quả logic của G; 
 End; 
Ví dụ 3.6 Giả giử G là tập hợp các câu tuyển sau 
 A B P (1) 
 C DP (2) 
 EC      (3) 
A       (4) 
E       (5) 
D       (6) 
Hãy chứng minh P. 
Ta thêm vào G câu sau: 
 P  (7) 
áp dụng luật giải cho câu (2) và (7) ta đƣợc câu: 
 108 
 C D (8) 
Từ câu (6) và (8) ta nhận đƣợc câu: 
 C  (9) 
Từ câu (3) và (9) ta nhận đƣợc câu: 
 E  (10) 
Tới đây đã xuất hiện mâu thuẫn, vì câu (5) và (10) đối lập nhau. 
Từ câu (5) và (10) ta nhận đƣợc câu rỗng. 
Vậy P đƣợc chứng minh. 
Ví dụ 3.7 Cho các câu sau: 
1) QT S 
2) APQ C 
3) PQ B 
4) B C  T 
5) PA 
6) PQ 
Hãy chuẩn hóa các câu và chứng minh S bằng phản chứng. 
- Chuẩn hóa: 
+ QT S  Q TS 
+ APQ C  A P QC 
+ PQ B  P QB 
- Thành lập các câu tuyển: 
 Q TS (1) 
 A P QC (2) 
 P QB (3) 
 B C  T (4) 
 PA (5) 
P (6) 
Q (7) 
- Chứng minh S bằng phản chứng: bổ sung S (8) 
- Từ (8), (1) Q T (9) 
- Từ (9), (7) T (10) 
- Từ (10), (4) B C (11) 
- Từ (5), (6) A (12) 
 109 
- Từ (12), (6), (7), (2) C (13) 
- Từ (3), (6), (7) B (14) 
- Từ (13), (14), (11) [] 
Kết luận: S đƣợc chứng minh. 
Ví dụ 3.8 Cho các câu sau: 
1) (AC) B F 
2) E  FA 
3) GF I 
4) (E F) B G 
5) BC 
Hãy chuẩn hóa các câu và chứng minh I bằng phản chứng. 
- Chuẩn hóa: 
+ (AC) B F  (AC)  B  F  ( A C) B  F  ( A B  F)( C B  F) 
+ GF I  G  F  I 
+ (E F) B G  (E F)  BG  ( E F)  BG  ( E  BG) ( F BG) 
- Thành lập các câu tuyển: 
 A B  F (1) 
 C B  F (2) 
 G  F  I (3) 
 E  BG (4) 
 F BG (5) 
 E  FA (5) 
B (6) 
C (7) 
- Chứng minh I bằng phản chứng: 
+ Bổ sung I (8) 
+ Từ (8), (3) G  F (9) 
+ Từ (6), (7), (2) F (10) 
+ Từ (9), (10) G (11) 
+ Từ (11), (5) F B (12) 
+ Từ (12), (10), (6) [] 
Kết luận: I đƣợc chứng minh. 
 110 
Ví dụ 3.9 Cho các câu sau: 
Nếu trời mƣa thì Lan mang theo dù 
Nếu Lan mang theo dù thì Lan không bị ƣớt 
Nếu trời không mƣa thì Lan không bị ƣớt 
a) Xây dựng các câu trên bằng các biểu thức logic mệnh đề 
b) Hãy chứng minh rằng"Lan không bị ƣớt" 
- Xây dựng các câu trên bằng các biểu thức logic mệnh đề 
R="Trời mƣa” 
U ="Lan mang theo dù” 
W ="Lan bị ƣớt” 
Lúc đó, ta có các biểu thức logic sau: 
R U (1) 
U W (2) 
 R W (3) 
- Chứng minh rằng"Lan không bị ƣớt" 
+ Giả sử"Lan bị ƣớt"tức là có W (4) 
+ Chuẩn hóa: 
(1) RU (5) 
(2) U W (6) 
(3) ( R) W  R W (7) 
+ Ta có: 
(4), (6) U (8) 
(8), (5) R (9) 
(9), (7) W (10) 
(10), (4) câu  
- Kết luận: W tứ là"Lan không bị ƣớt”. 
Ví dụ 3.10 Cho các câu sau: 
A F 
A (F P) 
PQ D 
A 
AD G 
Hãy chứng minh G. 
 111 
- Chuẩn hóa: 
A F  AF 
A (F P)  A  F  P 
PQ D  ( P Q)D  ( PD) ( Q  D) 
AD G  A D  G 
- Các công thức đã chuẩn hóa: 
 AF (1) 
 A  F  P (2) 
 PD (3) 
 Q  D (4) 
 A D  G (5) 
A (6) 
- Chứng minh bằng phản chức: 
Giả sử G (7) 
(7), (5) A D (8) 
(8), (6) D (9) 
(9), (3) P (10) 
(6), (1) F (11) 
(11), (2), (6) P (12) 
(12), (10) câu  
- Kết luận: G đƣợc chứng minh. 
Ví dụ 3.11 Cho các câu sau: 
A  B C 
 B  C D 
 D 
Chứng minh: A B. 
- Chuẩn hóa: 
A  B C  A  B  C 
 B  C D  B  C  D 
 D 
- Giả sử: (A B)  ( A  B)  A  B 
- Ta có: 
 A  B  C (1) 
 112 
 B  C  D (2) 
 D (4) 
A (5) 
 B (6) 
- (1), (2) A  D (7) 
- (7), (4) A (8) 
(8), (5) câu  
- Kết luận: A B. 
Ví dụ 3.12 Cho các câu sau: 
 113 
CÂU HỎI VÀ BÀI TẬP CHƢƠNG 3 
3.1.Trình bày cú pháp của logic mệnh đề gồm: các ký hiệu và các qui tắc xây dựng 
công thức. 
3.2.Trình bày khái niệm về literal, câu phân tử, câu phức, câu tuyển, câu Kowalski, 
câu Horn.Cho ví dụ minh họa. 
3.3. Khái niệm dạng chuẩn hội? Trình bày các bƣớc chuẩn hóa công thức về dạng 
chuẩn hội.Cho ví dụ minh họa. 
3.4. Trình bày các luật suy diễn Modus Ponens, Modus Tonens, Bắc cầu. Chứng minh 
các luật này bằng bảng chân lý. 
3.5.Trình bày các luật phân giải trên câu tuyển và câu Horn. 
3.6.Trình bày các luật suy diễn Loại bỏ hội, đƣa vào hội, đƣa vào tuyển, phân giải. 
3.7.Chứng minh các luật này bằng bảng chân lý. 
3.8.Trình bày thủ tục chứng minh bác bỏ bằng luật phân giải 
3.9. Chuẩn hóa công thức sau về dạng chuẩn hội: 
(A B) CD 
3.10. Cho các câu sau: 
 + (M N P) (Q R) 
 + (S N) (P Q) 
 + (M S) M 
Hãy chứng minh R bằng các cách sau: 
1. Sử dụng phƣơng pháp chứng minh diễn dịch 
2. Sử dụng phƣơng pháp chứng minh phản chứng. 
3.11. Cho các câu sau: 
 + (A B) (B C) 
 + ( C D) ( D E) 
 + E 
Chứng minh A bằng các cách sau: 
1. Sử dụng phƣơng pháp chứng minh diễn dịch. 
2. Sử dụng phƣơng pháp chứng minh phản chứng. 
3.12. Cho các câu sau: 
+ (M N) ( NP) 
 + (P Q) (QR) 
 + M 
Chứng minh R bằng hai cách: 
 114 
1. Sử dụng phƣơng pháp chứng minh diễn dịch. 
2. Sử dụng phƣơng pháp chứng minh phản chứng. 
3.12. Cho các câu sau: 
( AB C) ((DE) C) 
 E (AB) 
 A D 
Chứng minh C bằng hai cách: 
1. Sử dụng phƣơng pháp chứng minh diễn dịch. 
2. Sử dụng phƣơng pháp chứng minh phản chứng. 
3.13. Cho các câu sau: 
((BC) (GE)) (AD C) 
D BE 
A DC 
A 
Chuẩn hóa các câu về dạng chuẩn hội. 
Chứng minh G bằng hai cách: 
- Sử dụng phƣơng pháp chứng minh diễn dịch. 
- Sử dụng phƣơng pháp chứng minh phản chứng. 
3.14. Cho các câu sau 
(A B D) (B C F) 
( C D) ( D E) 
 E 
Chứng minh A bằng cách: 
1. Sử dụng phƣơng pháp chứng minh diễn dịch. 
2. Sử dụng phƣơng pháp chứng minh phản chứng. 
3.15Cho các câu sau 
+ A (B E) 
+ C (D P) 
+ (E C) (P Q) 
+ A 
+ B 
+ D 
1. Chuẩn hóa các câu về dạng chuẩn hội và thành lập các câu tuyển. 
2. Chứng minh Q bằng hai cách: 
 115 
a) Sử dụng phƣơng pháp chứng minh diễn dịch. 
b) Sử dụng phƣơng pháp chứng minh phản chứng. 
3.16. Cho các câu sau: 
+ B (A C) 
+ C (D P) 
+ A 
+ B 
+ D 
1. Chuẩn hóa các câu về dạng chuẩn hội và thành lập các câu tuyển. 
2. Chứng minh P bằng hai cách: 
a) Sử dụng phƣơng pháp chứng minh diễn dịch. 
b) Sử dụng phƣơng pháp chứng minh phản chứng. 
3.17. Cho các câu sau: 
+ A D BC 
+ A C 
+ B D 
+ A 
1. Chuẩn hóa các câu về dạng chuẩn hội và thành lập các câu tuyển. 
2. Chứng minh B bằng hai cách: 
a) Sử dụng phƣơng pháp chứng minh diễn dịch. 
b) Sử dụng phƣơng pháp chứng minh phản chứng. 
3.18. Cho các câu sau: 
 + (A (BC))  (DE) 
 + (A B) C 
1. Chuẩn hóa các câu về dạng chuẩn hội và thành lập các câu tuyển. 
2. Chứng minh A bằng hai cách: 
a) Sử dụng phƣơng pháp chứng minh diễn dịch. 
b) Sử dụng phƣơng pháp chứng minh phản chứng. 
3.19. Cho các câu sau: 
 + ( A (BC)) D 
 + (B C) E 
 + D B E 
1. Chuẩn hóa các câu về dạng chuẩn hội và thành lập các câu tuyển. 
2. Chứng minh C bằng hai cách: 
 116 
a) Sử dụng phƣơng pháp chứng minh diễn dịch. 
b) Sử dụng phƣơng pháp chứng minh phản chứng. 
3.20. Biểu thức nào trong số các biểu thức sau đây là vững chắc? 
a) P  Q  R P  Q 
b) (P Q) P 
c) ((P Q  (Q R)) (P R) 
3.21. Biểu thức nào trong số các biểu thức sau đây là vững chắc? 
a) P  Q  R P  Q 
b) (P Q) P 
c) ((P Q  (Q R)) (P R) 
3.22. Cho các câu sau: 
( PQ R) ((KE) R) 
 E (PQ) 
 P K 
Chứng minh R bằng hai cách: 
a) Sử dụng phƣơng pháp chứng minh diễn dịch. 
b) Sử dụng phƣơng pháp chứng minh phản chứng. 
3.23. Cho các câu sau: 
 + (P (QR))  (KE) 
 + (P Q) R 
1. Chuẩn hóa các câu về dạng chuẩn hội và thành lập các câu tuyển. 
2. Chứng minh P bằng hai cách: 
a) Sử dụng phƣơng pháp chứng minh diễn dịch. 
b) Sử dụng phƣơng pháp chứng minh phản chứng. 
3.24. Cho các câu sau: 
 + (A B C) (D E) 
 + (T B) (C D) 
 + (A T) A 
Hãy chứng minh E bằng các cách sau: 
1. Sử dụng phƣơng pháp chứng minh diễn dịch 
2. Sử dụng phƣơng pháp chứng minh phản chứng. 
3.25. Cho các câu sau: 
 + P  Q 
 + P R 
 117 
 + (Q  R) S 
Hãy chứng minh S bằng các cách 
1. Sử dụng phƣơng pháp chứng minh diễn dịch 
2. Sử dụng phƣơng pháp chứng minh phản chứng. 
3.26. Cho các câu sau: 
A F 
A (F P) 
PQ D 
A 
AD G 
1. Chuẩn hóa các câu về dạng chuẩn hội và thành lập các câu tuyển. 
2. Chứng minh G 
3.27. Cho các biểu thức logic mệnh đề sau 
NCD P 
QP C 
QC F  H 
 N PH 
NQ 
Hãy chứng minh F. 
3.28. Cho các biểu thức logic mệnh đề sau: 
AB C 
ABC P 
AS H 
ABCP S 
ABD 
Hãy chứng minh SH. 
3.29. CSTT của hệ chuyên gia về bệnh cảm cúm nhƣ sau: 
-"Nếu bệnh nhân rát họng và bị viêm nhiễm thì bệnh nhân bị viêm họng và bệnh nhân 
đi chữa họng" 
-"Nếu bệnh nhân có thân nhiệt >370 thì bệnh nhân bị sốt” 
-"Nếu bệnh nhân bị ốm trên 7 ngày và sốt thì bệnh nhân bị viêm nhiễm” 
-"Nếu bệnh nhân bị sốt và ho và kèm theo khó thở hoặc kèm theo tiếng rên thì bệnh 
nhân bị viêm phổi” 
a) Hãy biểu diễn các tri thức trên dƣới dạng logic mệnh đề. 
 118 
b) Có một bệnh nhân khai:"Thân nhiệt > 370"và"ốm trên 7 ngày”. Hãy dùng lập luận 
kết luận bệnh nhân này bị"viêm nhiễm". 
3.30. Cho CSTT mô tả mối quan hệ của các thành phần trong một tam giác: 
- Nếu biết 3 cạnh của 1 tam giác ta có thể biết nủa chu vi của tam giác đó 
- Nếu biết 2 cạnh và nữa chu vi của một tam giác thì ta có thể biết đƣợc cạnh còn lại 
của tam giác đó 
- Nếu biết đƣợc diện tích và một cạnh của một tam giác thì ta có thể biết đƣợc chiều 
cao tƣơng ứng với cạnh đó 
- Nếu biết 2 cạnh và một góc kẹp giữa 2 cạnh đó của một tam giác thì ta có thể biết 
đƣợc cạnh còn lại của tam giác đó. 
- Nếu biết 2 cạnh và một góc kẹp giữa 2 cạnh đó của một tam giác thì ta có thể biết 
đƣợc diện tích của tam giác đó 
- Nếu biết ba cạnh và nữa chu vi của một tam giác thì ta biết đƣợc diện tích của tam 
giác đó 
- Nếu biết diện tích và đƣờng cao của một tam giác thì ta biết đƣợc cạnh tƣơng ứng 
với đƣờng cao của tam giác đó 
Giả sử biết đƣợc 2 cạnh và và góc kẹp giữ hai cạnh đó. Hãy chứng minh rằng ta có 
thể suy ra đƣợc đƣờng cao tƣơng ứng với cạnh còn lại.