Giáo trình Logic chuyên ngành

ệ suy luận tự nhiên bao giờ cũng bắt đầu bằng giả thiết hay 
giả định. Sau đây là một số hệ logic với đặc điểm phụ thuộc do giáo sư Voisvillo e. K xây 
dựng. 
Hệ K1: Đặc điểm phụ thuộc (của công thức A nào đó trong chuỗi suy diễn vào các giả định và 
giả thiết) là một tập hợp các giả định, giả thiết (có thể là tập rỗng). Khái niệm công thức phụ 
thuộc vào giả định trong chuỗi suy diễn được định nghĩa quy nạp: 
a) Giả định (giả thiết) A phụ thuộc vào chính nó (và nghĩa là đặc điểm phụ thuộc của nó là 
tập hợp {A}); 
b) Sự phụ thuộc của các công thức khác được xác định theo các quy tắc suy luận. 
4 Voisvillo E. K. Các khía cạnh triết học – phương pháp luận của logic relevant. Moskva 1988. (Tiếng nga) 
9
9
Trong các quy tắc sau đây ta ký hiệu A, B, C, D là công thức bất kỳ; Γ, Δ là tập các công thức 
(có thể rỗng). Dấu phẩy giữa các tập hợp có nghĩa là dấu hội; “Γ \ Δ” có nghĩa là kết quả việc 
loại bỏ các thành phần thuộc Δ ra khỏi Γ : 
∧i : ],)[(
][],[
ΔΓ∧
ΔΓ
BA
BA ∧e : ( ][
])[(
Γ
Γ∧
A
BA ; 
][
])[(
Γ
Γ∧
B
BA ; 
∨i : ])[(
][
Γ∨
Γ
BA
A ; 
])[(
][
Γ∨
Γ
BA
B ; ∨e: ],,[
],[],,[
BAC
BCAC
∨ΔΓ
ΔΓ 
Trong đó A ∨ B là giả định có trước khi sử dụng quy tắc này trong chuỗi suy diễn. 
⊃i : }]{\)[(
][
ABA
B
Γ⊃
Γ với A là giả định bất kỳ trong chuỗi suy diễn. 
⊃e : ],[
][],)[(
ΔΓ
ΔΓ⊃
B
ABA ; ¬e: ][
][
Γ
⪪
A
A 
¬e : }]{\,[
][],[
AA
BB
ΔΓ¬
ΔΓ¬ với A là giả định bất kỳ trong chuỗi suy diễn. 
Chuỗi suy diễn là dãy các công thức (với đặc điểm phụ thuộc), trong đó mỗi công thức hoặc là 
một giả định, một giả thiết, hoặc là nhận được từ các công thức trước nó bằng cách sử dụng 
các quy tắc của hệ. Công thức cuối cùng được goị là kết luận. Nếu kết luận là công thức A [ Γ] 
thì : 
 Nếu Γ ≠ ∅, Γ = {B1, B2, , Bn}, ta nói A là hệ quả của các công thức B1, B2, , Bn. 
Viết Γ A. 
Nếu Γ = ∅ thì A là định lý, chuỗi suy diễn được gọi là phép chứng minh của công thức A. 
Trong hệ này các giả định có thể được sử dụng bao nhiêu lần cũng được, và chúng không bị 
loại bỏ khỏi suy luận. 
Ta nhận thấy rằng các quy tắc ∧i , ⊃i và ¬e không đảm bảo tính liên hệ về nội dung giữa tiền 
đề và kết luận. Thật vậy: 
Với ∧i , để ý rằng nếu trong chuỗi suy diễn, công thức giả định A không hề được sử 
dụng, thì kết luận của suy luận không phụ thuộc vào A. Thế nhưng bao giờ ta cũng có thể làm 
cho kết luận phụ thuộc vào một công thức bất kỳ, bằng cách sử dụng quy tắc ∧i, ∧e. Như thế 
mặc dầu không cần đến giả định A khi ta rút ra B, nhưng vẫn có thể coi là B phụ thuộc vào A. 
10
10
 Với ⊃i , nếu A ∉ Γ thì trong tiền đề B không phụ thuộc vào A, có nghĩa là B không 
được rút ra nhờ có A; còn ở kết luận Γ \ {A} = Γ, nhưng lại có B ⊃ A [Γ \ {A}}, hay A ⊃ B 
[Γ] và có nghĩa là B là hệ qủa của A trong điều kiện có Γ. Nghịch lý ở đây thể hiện khá rõ 
ràng. 
 Tương tự với ¬e. Nếu A ∉ Γ và A ∉ Δ thì B[Γ], ¬B[Δ] cho biết A không phải là 
một trong số các nguyên nhân làm xuất hiện mâu thuẫn B và ¬B. Thế nhưng từ đó quy tắc 
này lại cho phép rút ra ¬A [ Γ, Δ \ {A}], cứ như A là một trong những nguyên nhân gây ra 
mâu thuẫn B và ¬B vậy. Nghịch lý đã rõ ràng. 
2. Hệ suy luận tự nhiên relevant 
Để chuyển sang relevant logic, ta xét hệ K2 (tương đương K1), trong đó những vi phạm nguyên 
lý relevant (nguyên lý đảm bảo sự liên hệ về nội dung giữa tiền đề và kết luận) được gom về 
trong một quy tắc duy nhất. 
Hệ K2: Đặc điểm phụ thuộc bây giờ được hiểu là dãy các giả định (giả thiết); Γ, Δ là dãy bất 
kỳ của các giả định (công thức), và cũng có thể là dãy trống. 
Quy tắc: 
∧i : ])[(
][],[
Γ∧
ΓΓ
BA
BA ∧e : ( ][
])[(
Γ
Γ∧
A
BA ; 
][
])[(
Γ
Γ∧
B
BA ; 
∨i : ])[(
][
Γ∨
Γ
BA
A ; 
])[(
][
Γ∨
Γ
BA
B ; ∨e: ],[
],[],,[
BAC
BCAC
∨Γ
ΓΓ 
⊃i : ])[(
],[
Γ⊃
Γ
BA
AB ⊃e : ],[
][],)[(
ΔΓ
ΔΓ⊃
B
ABA 
¬e : 
],,[
],[],,[
*CA
CBAB
ΔΓ¬
ΔΓ¬ ¬e: ][
][
Γ
⪪
A
A 
trong đó *C là C nếu như C không trùng với A, và *C là dãy trống trong trường hợp ngược 
lại. 
],[
][
Γ
Γ
BA
A Quy tắc đơn điệu, với B là giả định bất kỳ trong chuỗi 
suy diễn. 
11
11
],,[
],,,[
ΔΓ
ΔΓ
BA
BBA Rút gọn đặc điểm phụ thuộc 
],,,[
],,,[
ΔΓ
ΔΓ
BCA
CBA Hoán vị đặc điểm phụ thuộc 
Các khái niệm chuỗi suy diễn và phép chứng minh định nghĩa như cũ. 
Nếu có chuỗi suy diễn với kết luận A [ Γ ] thì ta nói rằng A suy ra được từ tập Δ bất kỳ chứa 
tất cả các phần tử của dãy Γ. 
Bây giờ nếu ta thay khái niệm trên đây thành: Nếu có chuỗi suy diễn với kết luận A[Γ ] thì ta 
nói rằng A suy ra được từ tập công thức Δ, với Δ chứa tất cả các phần tử của Γ và Γ không 
rỗng (nghĩa là Γ chứa ít nhất một phần tử). 
Trong hệ thống này quy tắc duy hất không đảm bảo tính liên hệ về nội dung giữa tiền đề và kết 
luận (tính relevant) là quy tắc đơn điệu. Như vậy, loại bỏ quy tắc này, ta sẽ tránh được các 
nghịch lý. Hệ logic relevant thu được từ hệ K2 sau khi loại bỏ quy tắc đơn điệu được gọi là hệ 
RAO5. 
 Thay đổi chút ít hệ K2 ta được một trong những hệ logic relevant quan trọng nhất là hệ 
R6: Loại bỏ khỏi K2 quy tắc gây nghịch lý là quy tắc đơn điệu và thêm vào quy tắc phân phối 
của phép hội đối với phép tuyển 
]))[()((
]))[((
Γ∧∨∧
Γ∨∧
CABA
CBA 
Hệ En (tương đương với một hệ logic relevant nổi tiếng khác là hệ E) nhận được từ hệ trên 
bằng cách thay quy tắc hoán vị trong đặc điểm phụ thuộc bằng quy tắc hạn chế hoán vị trong 
đặc điểm phụ thuộc như sau: 
],),(,[
]),(,,[
Δ⊃Γ
Δ⊃Γ
BDCA
DCBA 
Chúng tôi cho rằng cơ sở lý luận thật sự của lập trình logic chính là logic relevant. Bởi vậy, 
việc nghiên cứu logic relevant lại càng có ý nghĩa. 
5 Giáo sư tiến sĩ Smirnov V.A. là người đưa ra thuật ngữ này, và ông cũng là người đầu tiên nghiên cứu hệ RAO. 
6 Chính xác hơn là ta được hệ suy luận tự nhiên tương đương với hệ R. 
BẢNG ĐỊNH NGHĨA CÁC PHÉP TOÁN LOGIC 
MỘT SỐ HẰNG ĐẲNG THỨC TRONG LOGIC MỆNH ĐỀ 
1. A + A = A; Luật đồng nhất, luật nuốt 
2. A . A = A; Luật đồng nhất, luật nuốt 
3. A + B = B + A Tính chất giao hoán của phép cộng 
4. A + (B + C) = (A+ B) + C Tính chất kết hợp của phép cộng 
5. A . B = B . A Tính chất giao hoán của phép nhân 
6. A . (B . C) = (A . B) . C Tính chất kết hợp của phép nhân 
7. A . (B + C) = A.B + A.C Tính phân phối của phép cộng đối với phép nhân 
8. A + (B . C) = (A + B) . (A + C ) Tính phân phối của phép nhân đối với phép cộng 
9. A + A = 1 ; Định nghĩa 1 
10. A . A = 0 ; Định nghĩa 0 
11. A = A Luật hoàn nguyên 
12. BA + = A . B Luật De Moorgan 
13. BA. = A + B Luật De Moorgan 
14. A.(A + B) = A Luật giản lược 
15. A + (A.B) = A Luật giản lược 
 A ¬A 
 T F 
 F T 
A B A & B A B A ∨ B 
T 
T 
F 
F 
 T 
 F 
 T 
 F 
 T 
 F 
 F 
 F 
 T 
 T 
 F 
 F 
 T 
 F 
 T 
 F 
 T 
 T 
 T 
 F 
A B A ⊃ B A B A ≡ B A B A ∨ B 
T 
T 
F 
F 
T 
F 
T 
F 
T 
F 
T 
T 
 T 
T 
F 
F 
T 
F 
T 
F 
T 
F 
F 
T 
 T 
 T 
 F 
 F 
 T 
 F 
 T 
 F 
 F 
 T 
 T 
 F 
Tuyển nghiêm ngặt Tương đương Kéo theo 
Tuyển không nghiêm ngặt Hội Phủ định 
CÁC KÝ HIỆU 
Ký hiệu Tên gọi Ví dụ sử dụng 
¬ Phủ định ¬ A 
& Hội A & B 
∨ Tuyển không nghiêm ngặt A ∨ B 
∨ Tuyển nghiêm ngặt A ∨ B 
⊃ Kéo theo A ⊃ B 
≡ Tương đương A ≡ B 
→ Kéo theo relevant, rút ra kết quả A → B; {p ∨ q, ¬ p ∨ r}→ q 
 Phủ định (trong đại số Boole) A 
. Hội (trong đại số Boole) A.B 
+ Tuyển (trong đại số Boole) A + B 
∀ Lượng từ toàn thể ∀xA(x) 
∃ Lượng từ tồn tại ∃xA(x) 
← , / Thế bằng x ← t, x/t 
term Hạn từ a là một term 
WFF Công thức A ∨ B là một WFF 
mgu Đồng nhất thể lớn nhất mgu(A,B) 
inf Thông tin Inf(A) 
U Toàn bộ thông tin inf(A) ≠ U 
T Đúng T(A→B)/α 
F Sai F(A→B)/α 
⊆ Là tập hợp con của hoặc bằng MA ⊆ MB 
∈ Thuộc về pi ∈ α 
∉ Không thuộc về pi ∉ α 
∅ Tập hợp rỗng MA ≠ ∅ 
|= Là quy luật logic, hệ quả |= A; Γ, A |= B 
|− Được chứng minh, định lý, rút ra |− A; Γ, A |− B 
⇔ Nghĩa là, tương đương với Inf(A) ⊆ inf (B) ⇔ MA ⊆ MB 
Fail Thất bại (trong hợp giải) fail
srqqp ¬∨∨∨ , 
 Resolvent rỗng ¬ p , p 
  
CÁC TIÊN ĐỀ VÀ QUY TẮC LOGIC MỆNH ĐỀ 
(1) Cho A, B, C là các công thức bất kỳ của hệ S . Khi đó các công thức sau đây là tiên 
đề của hệ S : 
(A1) (A ⊃ (B ⊃ A)); 
(A2) ((A ⊃ (B ⊃ C)) ⊃ ((A ⊃B) ⊃ (A ⊃ C)); 
(A3) (¬ B ⊃ ¬ A) ⊃ ((¬ B ⊃ A) ⊃ B)) 
(2) Quy tắc suy diễn duy nhất của S là Modus Ponens: 
B
ABAMP ,⊃ 
CÁC QUY TẮC CỦA HỆ SUY LUẬN TỰ NHIÊN TRONG LOGIC 
MỆNH ĐỀ 
Quy tắc nhập & (ký hiệu &i) BA
BA
&
, 
Quy tắc khử & (ký hiệu &e) A
BA & ; 
B
BA & 
Quy tắc nhập ∨ (ký hiệu ∨i) BA
A
∨ ; BA
B
∨ 
Quy tắc khử ∨ (ký hiệu ∨e) B
ABA ¬∨ , ; 
A
BBA ¬∨ , 
Quy tắc nhập ¬ (ký hiệu ¬i) A
BB
¬
¬, (*) 
Quy tắc khử ¬ (ký hiệu ¬e) A
A¬¬ 
Quy tắc nhập ⊃ (ký hiệu ⊃i) BA
B
⊃ (*) 
Quy tắc khử ⊃ (ký hiệu ⊃e) B
ABA ,⊃ 
CÁC TIÊN ĐỀ VÀ QUY TẮC LOGIC VỊ TỪ 
Các tiên đề 
Với mọi công thức A, B, C, và biến x bất kỳ, các biểu thức A1, A2, A3 sau đây là tiên đề 
của logic vị từ: 
A1. A ⊃ (B ⊃ A); 
A2. (A ⊃ (B ⊃ C)) ⊃ ((A ⊃ B) ⊃ (A ⊃ C)); 
A3. (¬A ⊃ ¬ B) ⊃ ((¬A ⊃ B) ⊃ A); 
A4. ∀x A(x) ⊃ A(t), với A(x) là công thức, t là hạn từ, tự do đối với x trong công 
thức A(x). 
A5. ∀x (A ⊃ B) ⊃ (A ⊃ ∀x B), nếu trong công thức A không có xuất hiện tự do của x. 
Các quy tắc 
1) 
B
ABAMP ,⊃ (Modus ponens) 
2) 
xA
AGen ∀ (Quy tắc tổng quát hóa) 
CÁC QUY TẮC CỦA HỆ SUY LUẬN TỰ NHIÊN LOGIC VỊ TỪ 
Các quy tắc của hệ suy luận tự nhiên logic mệnh đề 
Quy tắc nhập ∀ ( ký hiệu ∀i) )(
)(
xxA
xA
∀ x không xuất hiện tự do trong các 
giả thiết và giả định trước A(x) trong 
chuỗi suy diễn. 
Quy tắc khử ∀( ký hiệu ∀e) )(
)(
tA
xxA∀ t tự do đối với x trong A(x) 
Quy tắc nhập ∃ ( ký hiệu ∃i): )(
)(
xxA
tA
∃ t tự do đối với x trong A(x) 
Quy tắc khử ∃ (ký hiệu ∃e) )(
)(
cA
xxA∃ c là hằng đối tượng mới 
QUY TẮC HỆ SUY LUẬN TỰ NHIÊN LOGIC RELEVANT (HỆ K2) 
Đặc điểm phụ thuộc được hiểu là dãy các giả định (giả thiết), ghi trong cặp dấu ngoặc 
vuông; Γ, Δ là dãy bất kỳ của các giả định (công thức), và cũng có thể là dãy trống. 
∧i : ])[(
][],[
Γ∧
ΓΓ
BA
BA ∧e : ( ][
])[(
Γ
Γ∧
A
BA ; 
][
])[(
Γ
Γ∧
B
BA ; 
∨i : ])[(
][
Γ∨
Γ
BA
A ; 
])[(
][
Γ∨
Γ
BA
B ; ∨e: ],[
],[],,[
BAC
BCAC
∨Γ
ΓΓ 
⊃i : ])[(
],[
Γ⊃
Γ
BA
AB ⊃e : ],[
][],)[(
ΔΓ
ΔΓ⊃
B
ABA 
¬e : 
],,[
],[],,[
*CA
CBAB
ΔΓ¬
ΔΓ¬ ¬e: ][
][
Γ
⪪
A
A 
trong đó *C là C nếu như C không trùng với A, và *C là dãy trống trong trường hợp 
ngược lại. 
],[
][
Γ
Γ
BA
A Quy tắc đơn điệu, với B là giả định bất kỳ trong 
chuỗi suy diễn. 
],,[
],,,[
ΔΓ
ΔΓ
BA
BBA Rút gọn đặc điểm phụ thuộc 
],,,[
],,,[
ΔΓ
ΔΓ
BCA
CBA Hoán vị đặc điểm phụ thuộc 
MỤC LỤC 
LỜI NÓI ĐẦU 
CÁC KÝ HIỆU 
BẢNG ĐỊNH NGHĨA CÁC PHÉP TOÁN LOGIC 
MỘT SỐ HẰNG ĐẲNG THỨC TRONG LOGIC MỆNH ĐỀ 
CÁC TIÊN ĐỀ VÀ QUY TẮC LOGIC MỆNH ĐỀ 
CÁC QUY TẮC CỦA HỆ SUY LUẬN TỰ NHIÊN TRONG LOGIC MỆNH ĐỀ 
CÁC TIÊN ĐỀ VÀ QUY TẮC LOGIC VỊ TỪ 
CÁC QUY TẮC CỦA HỆ SUY LUẬN TỰ NHIÊN TRONG LOGIC VỊ TỪ 
QUY TẮC HỢP GIẢI 
QUY TẮC HỆ SUY LUẬN TỰ NHIÊN LOGIC RELEVANT (HỆ K2) 
Chương I LOGIC MỆNH ĐỀ 
I. Mệnh đề. Các phép toán trên mệnh đề 
1. Mệnh đề 
2. Các phép toán logic trên mệnh đề 
3. Định nghĩa các phép toán logic bằng phương pháp giải tích 
4. Công thức 
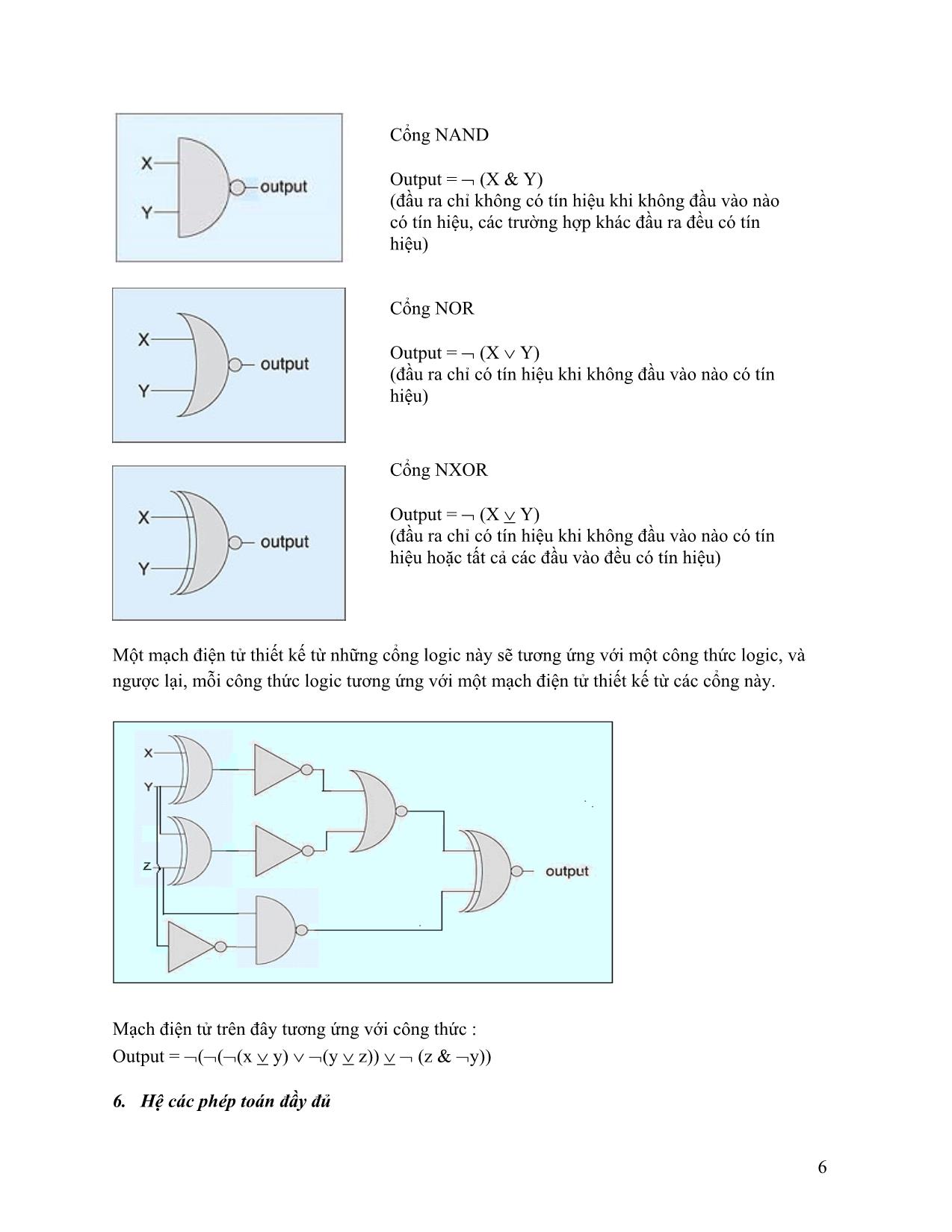
5. Các cổng logic trong kỹ thuật điện tử 
6. Hệ các phép toán đầy đủ 
II. Quy luật và mâu thuẫn logic 
1. Khái niệm quy luật và mâu thuẫn logic 
2. Các phương pháp xác định quy luật và mâu thuẫn logic 
III. Biến đổi tương đương 
1. Các ký hiệu và hằng đẳng thức 
2. Các ví dụ 
IV. Hệ tiên đề của logic mệnh đề 
1. Lý thuyết hình thức hóa (lý thuyết tiên đề hóa) 
2. Lý thuyết S (Hệ tiên đề S) 
3. Các hệ tiên đề khác của logic mệnh đề 
V. Hệ suy luận tự nhiên của logic mệnh đề 
1. Các quy tắc 
2. Chuỗi suy diễn và phép chứng minh 
3. Tính không mâu thuẫn và đầy đủ của các hệ S và NS 
Chương II HỢP GIẢI TRONG LOGIC MỆNH ĐỀ 
I. Công thức dạng tuyển 
1. Định nghĩa 
2. Quy trình INDO 
II. Quy tắc hợp giải 
III. Phương pháp hợp giải 
IV. Cây hợp giải. Hợp giải tuyến tính 
V. Giản lược tiền đề 
1. Giản lược tiền đề là quy luật logic 
2. Giản lược tiền đề một chiều 
3. Giản lược tiền đề yếu 
Chương 3 LOGIC VỊ TỪ 
I. Ngôn ngữ logic vị từ 
1. Phân tích ngôn ngữ tự nhiên 
2. Hệ ký tự 
3. Hạn từ (term) 
4. Công thức (WFF – Well Formed Formula) 
5. Các ví dụ 
6. Biểu thị tư tưởng bằng ngôn ngữ logic vị từ 
7. Biến tự do và biến buộc 
II. Diễn giải (Interpretation). Mô hình (Model) 
1. Diễn giải 
2. Giá trị chân lý của công thức trong diễn giải 
3. Mô hình (model). Quy luật logic 
III. Diễn giải Herbrand 
1. Miền herbrand 
2. Định nghĩa diễn giải herbrand và ví dụ 
3. Mô hình herbrand 
IV. Hệ tiên đề của logic vị từ 
1. Các tiên đề và quy tắc 
2. Chuỗi suy diễn, phép chứng minh 
3. Các tính chất cơ bản của hệ tiên đề logic vị từ 
V. Hệ suy luận tự nhiên của logic vị từ 
1. Các quy tắc 
2. Chuỗi suy diễn, phép chứng minh 
3. Một số ví dụ 
4. Tính không mâu thuẫn và đầy đủ của hệ suy luận tự nhiên 
Chương 4 HỢP GIẢI TRONG LOGIC VỊ TỪ 
I. Công thức dạng tuyển 
1. Định nghĩa 
2. Quy trình INSEADOR 
II. Phép thế 
1. Định nghĩa 
2. Áp dụng phép thế 
3. Tính bất biến của phép thế 
4. Phép thế hợp 
5. Quan hệ sắp xếp 
III. Đồng nhất thể 
1. Định nghĩa 
2. Đồng nhất thể lớn nhất 
IV. Quy tắc hợp giải 
V. Suy diễn hợp giải (chuỗi hợp giải) và phép chứng minh 
VI. Áp dụng 
1. Xác định tính mâu thuẫn của một tập công thức 
2. Trả lời câu hỏi đúng, sai 
3. Tìm kiếm câu trả lời 
VII. Giản lược tiền đề 
1. Giản lược tiền đề là quy luật logic 
2. Giản lược tiền đề một chiều 
3. Giản lược tiền đề yếu 
Chương 5 RELEVANT LOGIC 
I Dẫn nhập 
II. Nghịch lý của suy diễn logic và phép toán kéo theo 
1. Các nghịch lý 
2. Các cố gắng giải quyết nghịch lý 
III. Suy diễn logic – một quan hệ về nội dung, hay là về thông tin giữa 
các mệnh đề 
1. Các đặc điểm của quan hệ suy diễn logic 
2. Thông tin của mệnh đề. Nội dung logic là thông tin 
3. Nguyên nhân của nghịch lý suy diễn logic (cổ điển) 
IV Quan hệ suy diễn logic relevant 
V Xác định về mặt hình thức nguyên nhân nghịch lý của khái niệm 
kéo theo logic cổ điển. Hệ logic tự nhiên relevant 
1. Nguyên nhân nghịch lý của khái niệm kéo theo logic cổ điển về mặt 
hình thức 
2. Hệ suy luận tự nhiên relevant 
BÀI TẬP 
DANH MỤC TÀI LIỆU THAM KHẢO 
TÀI LIỆU THAM KHẢO 
1. Nguyễn Đức Dân. Logic và Tiếng Việt, NXB Giáo dục, Hà Nội 1996 
2. Nguyễn Đức Đồng, Nguyễn Văn Vĩnh. Logic toán, NXB Thanh Hóa 
3. Phạm Đình Nghiệm. Cơ sở phương pháp luận của lập trình logic, Luận án Phó tiến 
sĩ triết học, Moskva 1991 (Tiếng Nga). 
4. E. Mendencon. Nhập môn logic toán, NXB Khoa học, (Tiếng Nga). 
5. M. Genesereth. Computational logic .  
6. E.K. Voisvillo. Khía cạnh triết lý-nhận thức luận của logic relevant, Moskva 1988 
(Tiếng Nga). 
7. A.N. Kongomorov, A.G. Dragalin. Nhập môn logic toán, NXB Đại học Tổng hợp 
Moskva, 1982 (Tiếng Nga). 
8. Huge. Introduction to logic 
9. P. Tidman, H. Kanane. Logic and Philosophy. A modern introduction, Wadsworth 
Publishing Company.