Giáo trình Cấu trúc dữ liệu - Chương 13: Đồ thị
Một đồ thị (graph) G gồm một tập V chứa các đỉnh của đồ thị, và tập E chứa
các cặp đỉnh khác nhau từ V. Các cặp đỉnh này được gọi là các cạnh của G. Nếu e
= (ν, µ) là một cạnh có hai đỉnh ν và µ, thì chúng ta gọi ν và µ nằm trên e, và e
nối với ν và µ. Nếu các cặp đỉnh không có thứ tự, G được gọi là đồ thị vô hướng
(undirected graph), ngược lại, G được gọi là đồ thị có hướng (directed graph).
Thông thường đồ thị có hướng được gọi tắt là digraph, còn từ graph thường mang
nghĩa là đồ thị vô hướng. Cách tự nhiên để vẽ đồ thị là biểu diễn các đỉnh bằng
các điểm hoặc vòng tròn, và các cạnh bằng các đường thẳng hoặc các cung nối các
đỉnh. Đối với đồ thị có hướng thì các đường thẳng hay các cung cần có mũi tên chỉ
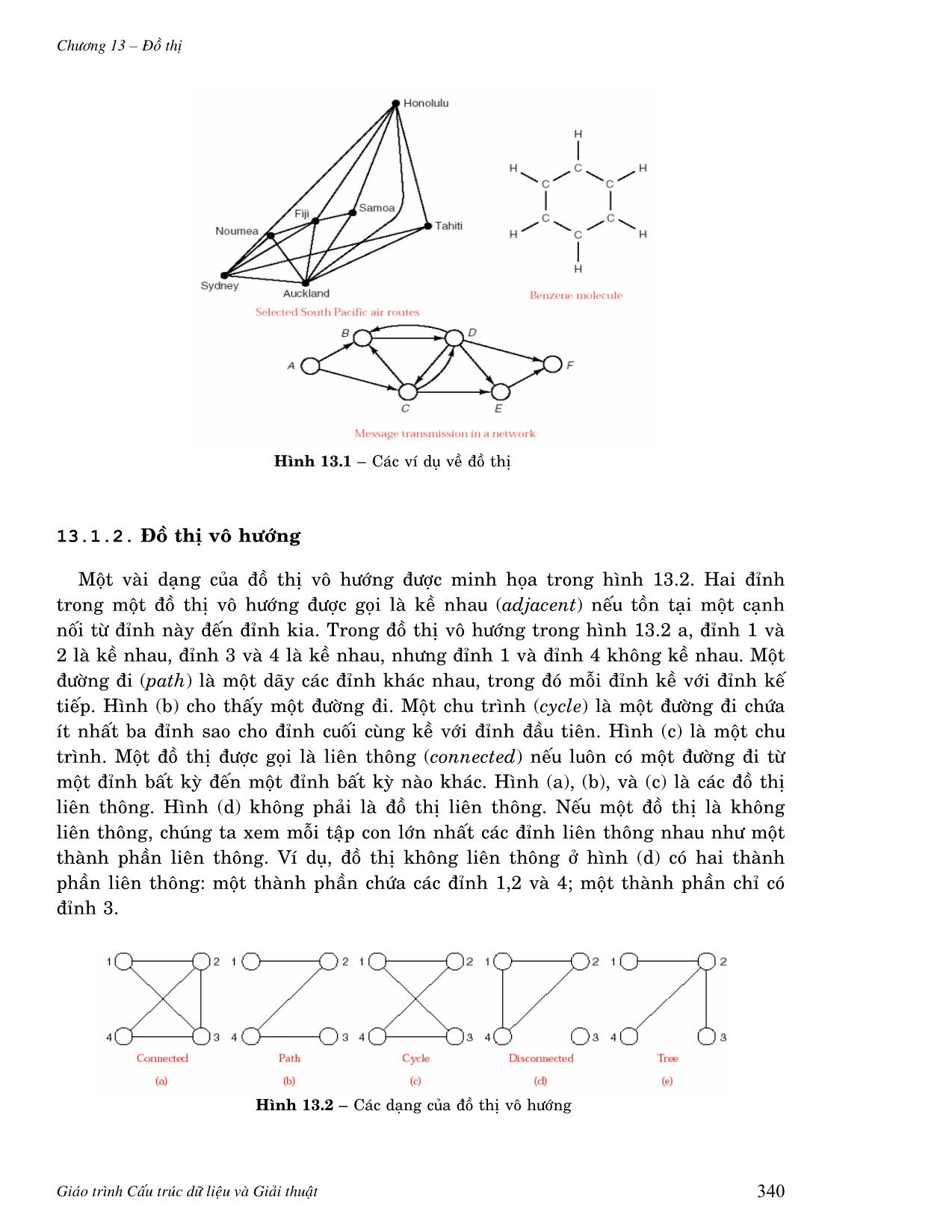
hướng. Hình 13.1 minh họa một số ví dụ về đồ thị.
Đồ thị thứ nhất trong hình 13.1 có các thành phố là các đỉnh, và các tuyến bay
là các cạnh. Trong đồ thị thứ hai, các nguyên tử hydro và carbon là các đỉnh, các
liên kết hóa học là các cạnh. Hình thứ ba là một đồ thị có hướng cho biết khả
năng truyền nhận dữ liệu trên mạng, các nút của mạng (A, B, , F) là các đỉnh và
các đường nối các nút là có hướng. Đôi khi cách chọn tập đỉnh và tập cạnh cho đồ
thị phụ thuộc vào giải thuật mà chúng ta dùng để giải bài toán, chẳng hạn bài
toán liên quan đến quy trình công việc, bài toán xếp thời khóa biểu,
Đồ thị được sử dụng để mô hình hóa rất nhiều dạng quá trình cũng như cấu
trúc khác nhau. Đồ thị có thể biểu diễn mạng giao thông giữa các thành phố, hoặc
các thành phần của một mạch in điện tử và các đường nối giữa chúng, hoặc cấu
trúc của một phân tử gồm các nguyên tử và các liên kết hóa học. Những người
dân trong một thành phố cũng có thể được biểu diễn bởi các đỉnh của đồ thị mà
các cạnh là các mối quan hệ giữa họ. Nhân viên trong một công ty có thể được
biểu diễn trong một đồ thị có hướng mà các cạnh có hướng cho biết mối quan hệ
của họ với những người quản lý. Những người này cũng có thể có những mối quan
hệ “cùng làm việc” biểu diễn bởi các cạnh không hướng trong một đồ thị vô
hướng.

Trang 1
Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Giáo trình Cấu trúc dữ liệu - Chương 13: Đồ thị

ược tạo bởi tất cả các đỉnh và một số cạnh của đồ thị G. Chúng
ta gọi những cây như vậy là cây phủ (spanning tree) của G. Cũng như phần trước,
chúng ta có thể xem một mạng trên một đồ thị G như là một bản đồ các tuyến
bay, với mỗi đỉnh biểu diễn một thành phố và tải trọng trên một cạnh là giá vé
bay từ thành phố này sang thành phố kia. Một cây phủ của G biểu diễn một tập
các đường bay cho phép các hành khách hoàn tất một chuyến du lịch qua khắp
các thành phố. Dĩ nhiên rằng, hành khách cần phải thực hiện một số tuyến bay
nào đó một vài lần mới hoàn tất được chuyến du lịch. Điều bất tiện này được bù
đắp bởi chi phí thấp. Nếu chúng ta hình dung mạng trong hình 13.11 như một hệ
thống điều khiển tập trung, thì đỉnh nguồn tương ứng với sân bay trung tâm, và
các đường đi từ đỉnh này là những hành trình bay. Một điều quan trọng đối với
một sân bay theo hệ thống điều khiển tập trung là giảm tối đa chi phí bằng cách
chọn lựa một hệ thống các đường bay mà tổng chi phí nhỏ nhất.
Định nghĩa: Một cây phủ tối tiểu (minimal spanning tree) của một mạng liên
thông là cây phủ mà tổng các tải trọng trên các cạnh của nó là nhỏ nhất.
Mặc dù việc so sánh hai cây phủ trong hình 13.12 là không khó khăn, nhưng
cũng khó mà biết được còn có cây phủ nào có trị nhỏ hơn nữa hay không. Bài toán
của chúng ta là xây dựng một phương pháp xác định một cây phủ tối tiểu của một
mạng liên thông.
Giáo trình Cấu trúc dữ liệu và Giải thuật 358
Chương 13 – Đồ thị
Hình 13.12 – Hai cây phủ trong một mạng
13.6.2. Phương pháp
Chúng ta đã biết giải thuật tìm cây phủ trong một đồ thị liên thông, do giải
thuật tìm đường ngắn nhất đã có. Chúng ta có thể thay đổi chút ít trong giải
thuật tìm đường ngắn nhất để có được phương pháp tìm cây phủ tối tiểu mà R. C.
Prim đã đưa ra lần đầu vào năm 1957.
Trước hết chúng ta chọn ra một đỉnh bắt đầu, gọi là nguồn, và trong khi tiến
hành phương pháp, chúng ta nắm giữ một tập X các đỉnh mà đường đi từ chúng
đến đỉnh nguồn thuộc về cây phủ tối tiểu mà chúng ta đã tìm thấy. Chúng ta cũng
cần nắm một tập Y gồm các cạnh nối các đỉnh trong X mà thuộc cây đang được
xây dựng. Như vậy, chúng ta có thể hình dung rằng các đỉnh trong X và các cạnh
trong Y đã tạo ra một phần của cây mà chúng ta cần tìm, cây này sẽ lớn lên
thành cây phủ tối tiểu cuối cùng. Lúc khởi đầu, đỉnh nguồn là đỉnh duy nhất
trong X, và Y là tập rỗng. Tại mỗi bước, chúng ta thêm một đỉnh vào X: đỉnh này
được chọn sao cho nó có một cạnh nối với một đỉnh nào đó đã có trong X có tải
trọng nhỏ nhất, so với các tải trọng của tất cả các cạnh khác nối các đỉnh còn
nằm ngoài X với các đỉnh đã có trong X. Cạnh tối tiểu này sẽ được đưa vào Y.
Việc chứng minh giải thuật Prim đem lại cây phủ tối tiểu không thực dễ dàng,
chúng ta tạm hoãn việc này lại sau. Tuy nhiên, chúng ta có thể hiểu về việc chọn
lựa một đỉnh mới để thêm vào X và một cạnh mới để thêm vào Y . Tiêu chí Prim
cho chúng ta một cách dễ dàng nhất để thực hiện việc kết nối này, và như vậy,
theo tiêu chí tham lam, chúng ta nên sử dụng nó.
Khi hiện thực giải thuật Prim, chúng ta cần nắm giữ một danh sách các đỉnh
thuộc X như là các phần tử của một mảng kiểu bool. Cách nắm giữ các cạnh
trong Y sẽ dễ dàng nếu như chúng ta bắt chước cách lưu trữ các cạnh trong một
đồ thị.
Giáo trình Cấu trúc dữ liệu và Giải thuật 359
Chương 13 – Đồ thị
Chúng ta sẽ cần đến một mảng phụ neighbor để biết thêm rằng, đối với mỗi
đỉnh ν, đỉnh nào trong X có cạnh đến ν có tải trọng nhỏ nhất. Các tải trọng nhỏ
nhất này cũng chứa trong mảng distance tương ứng. Nếu một đỉnh ν không có
một cạnh nào nối được với một đỉnh nào đó trong X, trị của phần tử tương ứng
của nó trong distance sẽ là infinity.
Hình 13.13 – Ví dụ về giải thuật Prim
Mảng neighbor được khởi tạo bằng cách gán neighbor[v] đến đỉnh nguồn
cho tất cả các đỉnh ν, và distance được khởi tạo bằng cách gán distance[v]
bởi tải trọng của cạnh nối từ đỉnh nguồn đến ν hoặc infinity nếu cạnh này
không tồn tại.
Để xác định đỉnh nào sẽ được thêm vào tập X tại mỗi bước, chúng ta chọn đỉnh
ν trong số các đỉnh chưa có trong X mà trị tương ứng trong mảng distance là
nhỏ nhất. Sau đó chúng ta cần cập nhật lại các mảng để phản ánh đúng sự thay
đổi mà chúng ta đã làm đối với tập X như sau: với mỗi w chưa có trong X, nếu có
Giáo trình Cấu trúc dữ liệu và Giải thuật 360
Chương 13 – Đồ thị
một cạnh nối ν và w, chúng ta xem thử tải trọng của cạnh này có nhỏ hơn
distance[w] hay không, nếu quả thực như vậy thì distance[w] cần được cập
nhật lại bằng trị của tải trọng này, và neighbor[w] sẽ là ν.
Lấy ví dụ, chúng ta hãy xem xét mạng trong hình (a) của hình 13.13. Trạng
thái ban đầu trong hình (b): Tập X (các đỉnh được tô màu) chỉ gồm đỉnh nguồn 0,
và đối với mỗi đỉnh w, đỉnh được lưu trong neighbor[w] được chỉ bởi các mũi tên
từ w. Trị của distance[w] là tải trọng của cạnh tương ứng. Khoảng cách từ
nguồn đến đỉnh 1 là một trong những trị nhỏ nhất, nên 1 được thêm vào X như
hình (c), và trong các phần tử của các mảng neighbor và distance chỉ có các
phần tử tương ứng với đỉnh 2 và đỉnh 5 là được cập nhật lại. Đỉnh kế tiếp gần với
các đỉnh trong X nhất là đỉnh 2, nó được thêm vào X như hình (d), trong này
cũng đã chỉ ra các trị của các mảng đã được cập nhật lại. Các bước cuối cùng được
minh họa trong hình (e), (f) và (g).
13.6.3. Hiện thực
Để hiện thực giải thuật Prim, chúng ta cần chọn một lớp để biểu diễn cho
mạng. Sự tương tự của giải thuật này so với giải thuật tìm đường ngắn nhất trong
phần trước giúp chúng ta quyết định thiết kế lớp Network dẫn xuất từ lớp
Digraph.
template
class Network: public Digraph {
public:
Network();
void read(); // Định nghĩa lại để nhập thông tin về mạng.
void make_empty(int size = 0);
void add_edge(Vertex v, Vertex w, Weight x);
void minimal_spanning(Vertex source,
Network &tree) const;
};
Chúng ta sẽ viết lại phương thức nhập read để đảm bảo rằng tải trọng của
cạnh (ν, w) luôn trùng với tải trọng của cạnh (w, ν), với mọi ν và w, vì đây là một
mạng vô hướng. Phương thức mới make_empty(int size) tạo một mạng có
size đỉnh và không có cạnh. Phương thức khác, add_edge, thêm một cạnh có
một tải trọng cho trước vào mạng. Chúng ta cũng đã giả sử rằng lớp Weight đã có
đầy đủ các toán tử so sánh. Ngoài ra, người sử dụng cần khai báo trị lớn nhất có
thể của Weight gọi là infinity. Phương thức minimal_spanning mà chúng ta
sẽ viết ở đây sẽ tìm cây phủ tối tiểu và trả về qua tham biến tree. Tuy phương
thức chỉ có thể tìm cây phủ khi thực hiện trên một mạng liên thông, nó cũng có
thể tìm một cây phủ cho một thành phần liên thông có chứa đỉnh source trong
mạng.
Giáo trình Cấu trúc dữ liệu và Giải thuật 361
Chương 13 – Đồ thị
template
void Network::minimal_spanning(Vertex source,
Network &tree) const
/*
post: Xác định cây phủ tối tiểu trong thành phần liên thông có chứa đỉnh source của mạng.
*/
{
tree.make_empty(count);
bool component[graph_size]; // Các đỉnh trong tập X.
Vertex neighbor[graph_size];// Phần tử thứ i chứa đỉnh trước của nó sao cho khoảng
// cách giữa chúng nhỏ nhất so với các khoảng cách từ
// các đỉnh trước khác đã có trong tập X đến nó.
Weight distance[graph_size];// Các khoảng cách nhỏ nhất tương ứng với từng phần tử
// trong mảng neighbor trên.
Vertex w;
for (w = 0; w < count; w++) {
component[w] = false;
distance[w] = adjacency[source][w];
neighbor[w] = source;
}
component[source] = true; // Tập X chỉ có duy nhất đỉnh nguồn.
for (int i = 1; i < count; i++) {
Vertex v; // Mỗi lần lặp bổ sung thêm một đỉnh vào tập X.
Weight min = infinity;
for (w = 0; w < count; w++) if (!component[w])
if (distance[w] < min) {
v = w;
min = distance[w];
}
if (min < infinity) {
component[v] = true;
tree.add_edge(v, neighbor[v], distance[v]);
for (w = 0; w < count; w++) if (!component[w])
if (adjacency[v][w] < distance[w]) {
distance[w] = adjacency[v][w];
neighbor[w] = v;
}
}
else break; // Xong một thành phần liên thông trong đồ thị không liên thông.
}
}
Vòng lặp chính trong hàm trên thực hiện n-1 lần, với n là số đỉnh, và trong
vòng lặp chính còn có hai vòng lặp khác, mỗi vòng lặp này thực hiện n-1 lần. Vậy
các vòng lặp thực hiện (n-1)2 lần. Các lệnh bên ngoài vòng lặp chỉ hết O(n), nên
thời gian chạy của hàm là O(n2).
13.6.4. Kiểm tra giải thuật Prim
Chúng ta cần chứng minh rằng, đối với đồ thị liên thông G, cây phủ S sinh ra
bởi giải thuật Prim phải có tổng tải trọng trên các cạnh nhỏ hơn so với bất kỳ
Giáo trình Cấu trúc dữ liệu và Giải thuật 362
Chương 13 – Đồ thị
một cây phủ nào khác của G. Giải thuật Prim xác định một chuỗi các cạnh s1, s2,
..., sn tạo ra cây phủ S. Như hình 13.14, s1 là cạnh thứ nhất được thêm vào tập Y
trong giải thuật Prim, s2 là cạnh thứ hai được thêm vào, và cứ thế.
Để chứng minh S là một cây phủ tối tiểu, chúng ta chứng minh rằng nếu m là
một số nguyên, 0 ≤ m ≤ n, thì sẽ có một cây phủ tối tiểu chứa cạnh si với i ≤ m.
Chúng ta sẽ chứng minh quy nạp trên m. Trường hợp cơ bản, khi m = 0, rõ ràng
là đúng, vì bất kỳ cây phủ tối tiểu nào cũng đều phải chứa một tập rỗng các cạnh.
Ngoài ra, khi chúng ta hoàn tất việc quy nạp, trường hợp cuối cùng với m = n chỉ
ra rằng có một cây phủ tối tiểu chứa tất cả các cạnh của S, và chính là S. (Lưu ý
rằng nếu thêm bất kỳ một cạnh nào vào một cây phủ thì cũng tạo ra một chu
trình, nên bất kỳ cây phủ nào chứa mọi cạnh của S đều phải chính là S). Nói cách
khác, khi chúng ta hoàn tất việc quy nạp, chúng ta đã chứng minh được rằng S
chính là cây phủ tối tiểu.
Như vậy chúng ta cần trình bày các bước quy nạp bằng cách chứng minh rằng
nếu m < n và T là một cây phủ tối tiểu chứa các cạnh s i với i ≤ m, thì phải có một
cây phủ tối tiểu U cũng chứa các cạnh trên và thêm một cạnh sm+1. Nếu sm+1 đã có
trong T, chúng ta có thể đơn giản cho U = T, như vậy chúng ta có thể giả sử rằng
sm+1 không là một cạnh trong T. Chúng ta hãy xem hình (b) của hình 13.14.
Hình 13.14 – Kiểm tra giải thuật Prim
Chúng ta hãy gọi X là tập các đỉnh trong S thuộc các cạnh s1, s2, ..., sm và R là
tập các đỉnh còn lại trong S. Trong giải thuật Prim, cạnh sm+1 nối một đỉnh trong
Giáo trình Cấu trúc dữ liệu và Giải thuật 363
Chương 13 – Đồ thị
X với một đỉnh trong R, và sm+1 là một trong các cạnh có tải trọng nhỏ nhất nối
giữa hai tập này. Chúng ta hãy xét ảnh hưởng của việc thêm cạnh sm+1 này vào T,
như minh họa trong hình (c). Việc thêm vào này phải tạo ra một chu trình C, do
mạng liên thông T rõ ràng là có chứa một đường đi có nhiều cạnh nối hai đầu của
cạnh sm+1. Chu trình C phải có chứa một cạnh t ≠ sm+1 nối tập X với tập R, do nếu
chúng ta di dọc theo đường đi khép kín C chúng ta phải đi vào tập X một số lần
bằng với số lần chúng ta đi ra khỏi nó. Chúng ta hãy xem hình (d). Giải thuật
Prim bảo đảm rằng tải trọng của sm+1 nhỏ hơn hoặc bằng tải trọng của t. Do đó,
cây phủ mới U trong hình (e), có được từ T bằng cách loại đi t và thêm vào sm+1,
sẽ có tổng tải trọng không lớn hơn tải trọng của T. Như vậy chúng ta đã có được
U là một cây phủ tối tiểu của G, mà U chứa các cạnh s1, s2, ..., sm, sm+1. Điều này
hoàn tất được quá trình quy nạp của chúng ta.
13.7. Sử dụng đồ thị như là cấu trúc dữ liệu
Trong chương này, chúng ta đã tìm hiểu chỉ một ít ứng dụng của đồ thị, nhưng
chúng ta đã bắt đầu thâm nhập vào những vấn đề sâu sắc của các giải thuật về đồ
thị. Nhiều giải thuật trong số đó, đồ thị xuất hiện như các cấu trúc toán học và đã
nắm bắt được các đặc trưng thiết yếu của bài toán, thay vì chỉ là những công cụ
tính toán cho ra được những lời giải của chúng. Lưu ý rằng trong chương này
chúng ta đã nói về các đồ thị như là các cấu trúc toán học, chứ không như các cấu
trúc dữ liệu, do chúng ta đã sử dụng chúng để đặc tả các vấn đề trong toán học,
và để viết các giải thuật, chúng ta đã hiện thực các đồ thị trong các cấu trúc dữ
liệu như danh sách hoặc bảng. Tuy vậy, rõ ràng là đồ thị tự bản thân nó có thể
được xem như các cấu trúc dữ liệu - các cấu trúc dữ liệu mà có chứa các mối quan
hệ giữa các dữ liệu phức tạp hơn những gì đã được mô tả trong một danh sách
hoặc một cây. Do tính tổng quát và mềm dẻo, đồ thị là cấu trúc dữ liệu rất hiệu
quả và đã tỏ rõ những giá trị của nó trong những ứng dụng cấp tiến như thiết kế
hệ quản trị cơ sở dữ liệu chẳng hạn. Tất nhiên, một công cụ mạnh như vậy càng
nên được sử dụng mọi khi cần thiết, nhưng việc sử dụng nó cần phải được kết hợp
với việc xem xét một cách cẩn thận để sức mạnh của nó không làm cho cho chúng
ta bị rối. Cách an toàn nhất trong việc sử dụng một công cụ mạnh là dựa trên sự
chính quy; nghĩa là, chúng ta chỉ sử dụng công cụ mạnh trong những phương
pháp đã được định nghĩa một cách cẩn thận và dễ hiểu. Do tính tổng quát của đồ
thị, việc tuân thủ nguyên tắc vừa nêu ra trong việc sử dụng nó không phải luôn dễ
dàng.
Giáo trình Cấu trúc dữ liệu và Giải thuật 364File đính kèm:
 giao_trinh_cau_trsuc_du_lieu_chuong_13_do_thi.pdf
giao_trinh_cau_trsuc_du_lieu_chuong_13_do_thi.pdf

