Giải thuật tSVM cho phân lớp phi tuyến tập dữ liệu lớn
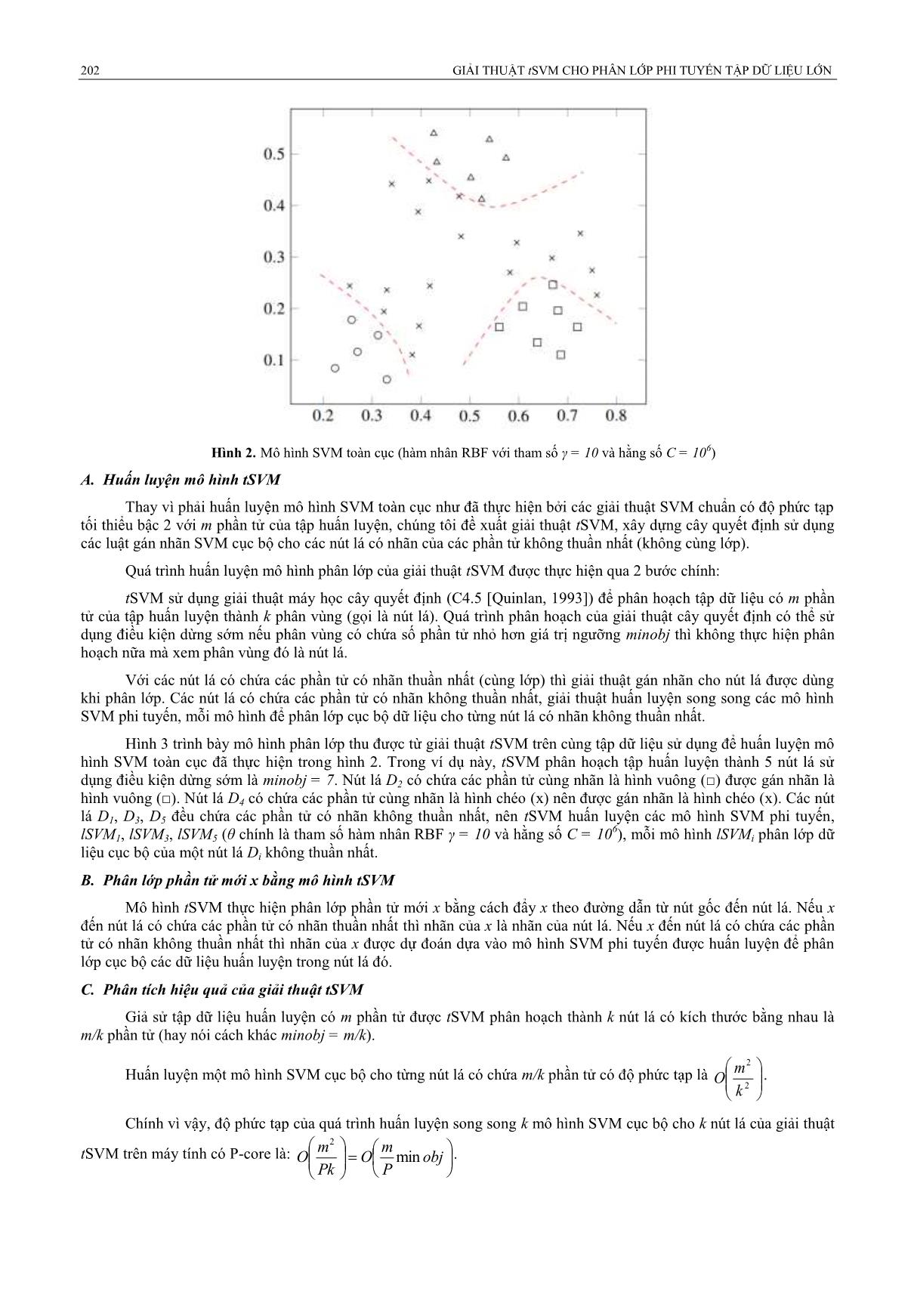
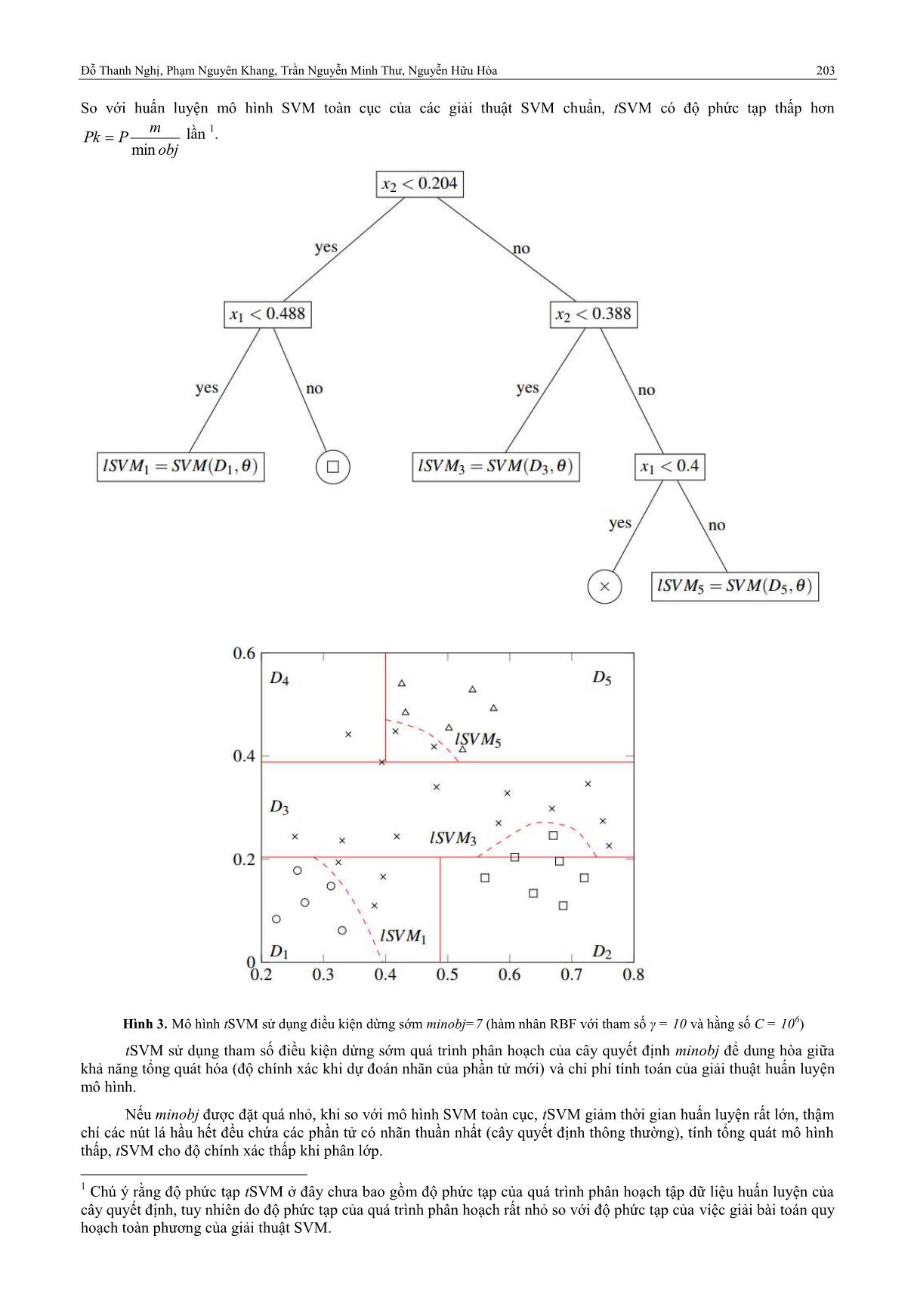
TÓM TẮT— Trong bài viết này, chúng tôi trình bày giải thuật tSVM cho phân lớp phi tuyến tập dữ liệu lớn. Giải thuật tSVM sử dụng máy học cây quyết định để phân hoạch nhanh tập dữ liệu lớn thành k phân vùng được gọi là nút lá. Chỉ những nút lá có nhãn (lớp) của các phần tử thuần nhất (giống nhau) được giải thuật tSVM gán nhãn tương ứng như giải thuật cây quyết định dùng để phân lớp. Với mỗi nút lá có nhãn các phần tử không thuần nhất, giải thuật tSVM huấn luyện một mô hình SVM phi tuyến dùng để phân lớp dữ liệu cục bộ của nút lá. Việc huấn luyện các mô hình SVM trên từng nút lá có nhãn không thuần nhất hoàn toàn độc lập với nhau, vì thế có thể được thực hiện song song trên các máy tính multi-Core. Kết quả thực nghiệm trên các tập dữ liệu của UCI và 3 tập dữ liệu nhận dạng ký tự viết tay và tập dữ liệu phân lớp ảnh cho thấy giải thuật tSVM cho kết quả phân lớp nhanh, chính xác khi so sánh với giải thuật SVM chuẩn như LibSVM

Trang 1

Trang 2
Trang 3
Trang 4

Trang 5
Trang 6

Trang 7

Trang 8

Trang 9
Tóm tắt nội dung tài liệu: Giải thuật tSVM cho phân lớp phi tuyến tập dữ liệu lớn

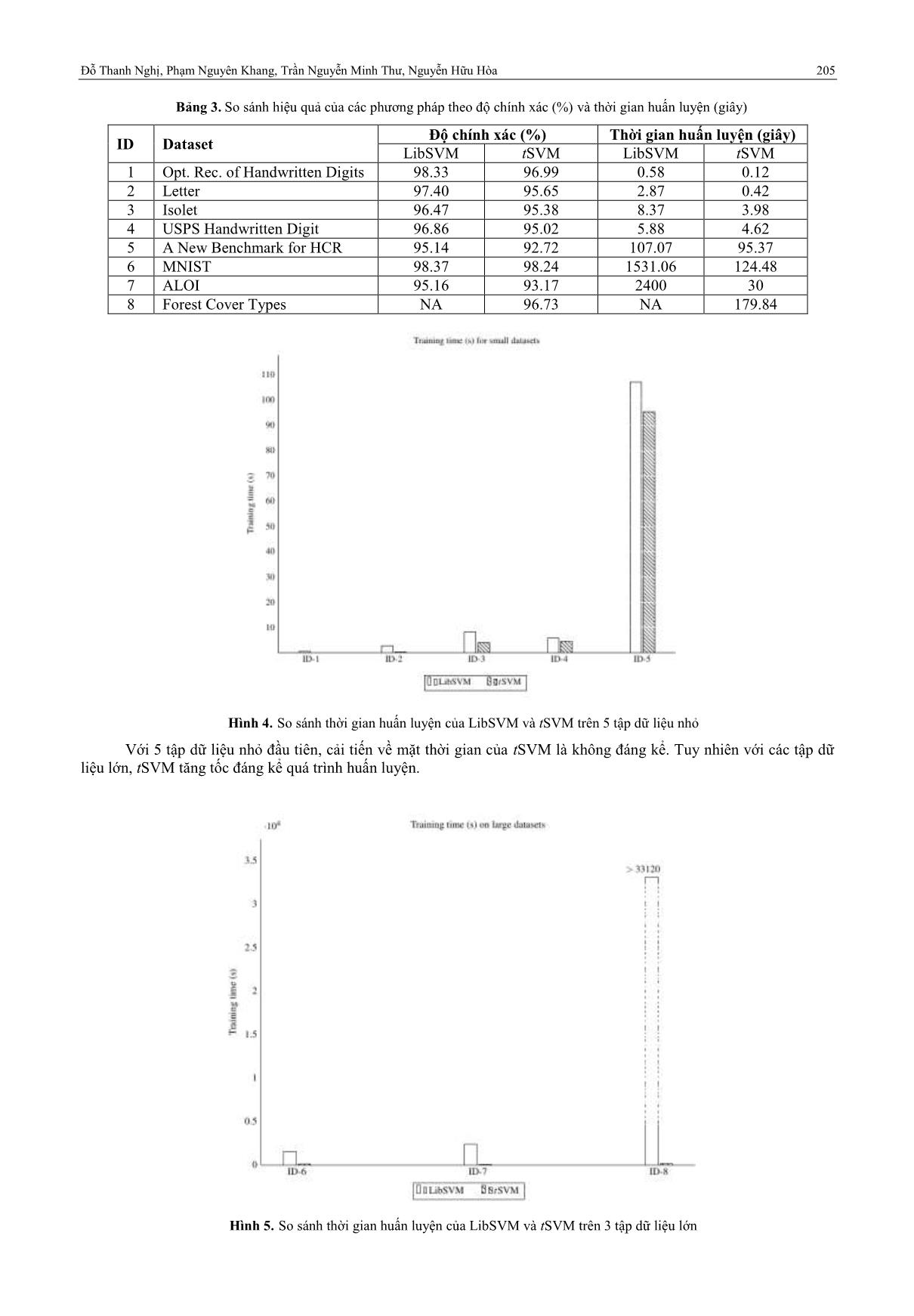
a trên hai tiêu chí: độ chính xác phân lớp và thời gian huấn luyện. Tất cả các thí nghiệm được chạy trên máy tính cá nhân, cài hệ điều hành Linux Fedora 20, bộ vi xử lý Intel® Core i7-4790, 3.6 GHz, 4 nhân và bộ nhớ RAM 32 GB. B. Chuẩn bị tập dữ liệu Thí nghiệm được thực hiện trên 4 tập dữ liệu UCI [Lichman, 2013] và 3 bộ dữ liệu ký tự viết tay chuẩn hai bộ cũ: USPS [Lecun et al., 1989], MNIST [Lecun et al., 1998], một bộ dữ liệu ký tự viết tay mới [van der Maaten, 2009] và tập dữ liệu phân lớp ảnh [Geusebroek et al., 2005]. Bảng 1 trình bày mô tả của các tập dữ liệu thực nghiệm. Nghi thức kiểm tra đánh giá được chỉ ra trong cột cuối của bảng. Dữ liệu đã được chia thành hai tập: huấn luyện (Trn) và kiểm tra (Tst). Chúng tôi sử dụng tập huấn luyện để huấn luyện các mô hình SVM. Sau đó, sử dụng các mô hình phân lớp thu được để phân lớp dữ liệu trong tập kiểm tra. Bảng 1. Mô tả các tập dữ liệu thực nghiệm ID Dataset Số phần tử Số thuộc tính Số lớp Nghi thức kiểm tra 1 Opt. Rec. of Handwritten Digits 5620 64 10 3832 Trn - 1797 Tst 2 Letter 20000 16 26 13334 Trn - 6666 Tst 3 Isolet 7797 617 26 6238 Trn - 1559 Tst 4 USPS Handwritten Digit 9298 256 10 7291 Trn - 2007 Tst 5 A New Benchmark for HCR 40133 3136 36 36000 Trn - 4133 Tst 6 MNIST 70000 784 10 60000 Trn - 10000 Tst 7 ALOI 108000 128 1000 72000 Trn - 36000 Tst 8 Forest Cover Types 581012 54 7 400000 Trn - 181012 Tst C. Điều chỉnh tham số Chúng tôi đề xuất sử dụng hàm nhân RBF trong cả tSVM và LibSVM vì tính tổng quát và tính hiệu quả của nó [Chang & Lin, 2011]. Chúng tôi cũng điều chỉnh siêu tham số γ của hàm nhân RBF và hằng số C (tham số dung hòa lỗi và độ rộng của lề SVM) để có được kết quả cao nhất. Hơn nữa giải thuật tSVM của chúng tôi có sử dụng thêm một tham số điều kiện dừng sớm quá trình phân hoạch của cây quyết định minobj được đặt bằng 1000 phần tử (nhằm tạo ra một sự dung hòa giữa độ chính xác của mô hình phân lớp và chi phí tính toán). Bảng 2 trình bày các siêu tham số được sử dụng cho tSVM và LibSVM. Bảng 2. Các tham số của tSVM và LibSVM ID Dataset C Minobj 1 Opt. Rec. of Handwritten Digits 0.0001 100000 1000 2 Letter 0.0001 100000 1000 3 Isolet 0.0001 100000 1000 4 USPS Handwritten Digit 0.0001 100000 1000 5 A New Benchmark for HCR 0.001 100000 1000 6 MNIST 0.05 100000 1000 7 ALOI 0.01 100000 1000 8 Forest Cover Types 0.0001 100000 1000 D. Kết quả phân lớp Kết quả phân lớp của LibSVM và tSVM trên 8 tập dữ liệu được cho trong bảng 3 và các hình 4, 5 và 6. Như mong đợi, giải thuật tSVM của chúng tôi có thời gian huấn luyện ngắn hơn nhiều so với giải thuật LibSVM. Về tiêu chí độ chính xác phân lớp, giải thuật của chúng tôi cho kết quả có thể so sánh được với giải thuật LibSVM. Đỗ Thanh Nghị, Phạm Nguyên Khang, Trần Nguyễn Minh Thư, Nguyễn Hữu Hòa 205 Bảng 3. So sánh hiệu quả của các phương pháp theo độ chính xác (%) và thời gian huấn luyện (giây) ID Dataset Độ chính xác (%) Thời gian huấn luyện (giây) LibSVM tSVM LibSVM tSVM 1 Opt. Rec. of Handwritten Digits 98.33 96.99 0.58 0.12 2 Letter 97.40 95.65 2.87 0.42 3 Isolet 96.47 95.38 8.37 3.98 4 USPS Handwritten Digit 96.86 95.02 5.88 4.62 5 A New Benchmark for HCR 95.14 92.72 107.07 95.37 6 MNIST 98.37 98.24 1531.06 124.48 7 ALOI 95.16 93.17 2400 30 8 Forest Cover Types NA 96.73 NA 179.84 Hình 4. So sánh thời gian huấn luyện của LibSVM và tSVM trên 5 tập dữ liệu nhỏ Với 5 tập dữ liệu nhỏ đầu tiên, cải tiến về mặt thời gian của tSVM là không đáng kể. Tuy nhiên với các tập dữ liệu lớn, tSVM tăng tốc đáng kể quá trình huấn luyện. Hình 5. So sánh thời gian huấn luyện của LibSVM và tSVM trên 3 tập dữ liệu lớn 206 GIẢI THUẬT tSVM CHO PHÂN LỚP PHI TUYẾN TẬP DỮ LIỆU LỚN Xét thời gian huấn luyện mô hình phân lớp cho tập dữ liệu MNIST, giải thuật tSVM nhanh hơn LibSVM đến 12.30 lần. Xét thời gian huấn luyện mô hình phân lớp cho tập dữ liệu ảnh ALOI. Tập dữ liệu này rất đặc biệt do có số phần tử lớn và số lớp của đối tượng là 1000, nếu huấn luyện mô hình đa lớp bằng cách xây dựng mô hình phân lớp nhị phân cho từng cặp lớp như LibSVM thì cần đến 499500 mô hình nhị phân. Trong khi đó, tSVM đã phân hoạch tập huấn luyện có 1000 lớp thành các phân vùng con, mỗi phân vùng có số lớp ít hơn so với tập huấn luyện đầy đủ. Kết quả là giải thuật tSVM nhanh hơn LibSVM đến 80 lần. Đặc biệt, với tập dữ liệu Forest cover type (được xem như là tập dữ liệu khó đối với SVM phi tuyến [Yu et al., 2003], [Do & Poulet, 2004], LibSVM chạy đến 23 ngày vẫn chưa hoàn thành quá trình huấn luyện mô hình. Trong khi đó, tSVM thực hiện huấn luyện trong 179.8 giây (3 phút) và cho độ chính xác phân lớp là 96.73%. Hình 6. So sánh độ chính xác phân lớp của LibSVM và tSVM trên 8 tập dữ liệu V. CÁC NGHIÊN CỨU LIÊN QUAN Để cải tiến việc huấn luyện giải thuật máy học SVM cho các tập dữ liệu lớn, các công trình nghiên cứu trong [Boser et al., 1992], [Chang & Lin, 2011], [Osuna et al., 1997], [Platt, 1998] đã chia bài toán quy hoạch toàn phương gốc thành các bài toán con để giải quyết. Nghiên cứu của chúng tôi liên quan đến các giải thuật huấn luyện mô hình phân lớp phi tuyến cục bộ. Nhóm các giải thuật huấn luyện mô hình phân cấp cho vấn đề phân lớp, thực hiện phân lớp qua 2 bước chính: gom nhóm tập dữ liệu huấn luyện thành k nhóm (clusters); bước tiếp theo là huấn luyện các mô hình phân lớp cục bộ cho từng nhóm. Đề xuất của [Jacobs et al., 1991] sử dụng giải thuật cực đại kỳ vọng (Expectation-Maximization, EM [Dempster et al., 1977]) để chia dữ liệu thành k nhóm không tách rời (joint clusters); và huấn luyện các mô hình mạng nơ-ron (Neural Network) để phân lớp dữ liệu cục bộ cho từng nhóm. Nghiên cứu của [Collobert et al., 2002] chỉ khác với nghiên cứu của [Jacobs et al., 1991] là xây dựng k mô hình SVM [Vapnik, 1995] cục bộ. CSVM [Gu & Han, 2013] sử dụng giải thuật k-means [MacQueen, 1967] để phân hoạch tập dữ liệu huấn luyện thành k nhóm tách biệt; sau đó huấn luyện các mô hình SVM tuyến tính có trọng số từ các nhóm dữ liệu. Nghiên cứu gần nhất là giải thuật kSVM [Do, 2015] và krSVM [Do & Poulet, 2015] xây dựng song song k mô hình SVM phi tuyến cục bộ trên máy tính đa nhân, bộ nhớ chia sẻ, để phân lớp cục bộ k nhóm, được phân hoạch từ tập dữ liệu huấn luyện với k-means. DTSVM [Chang et al., 2010] sử dụng giải thuật học cây quyết định [Breiman et al., 1984], [Quinlan, 1993] để phân hoạch tập dữ liệu huấn luyện thành các phân vùng tách rời nhau và xây dựng các mô hình SVM cục bộ cho các phân vùng. Các giải thuật này đều nhằm cải tiến tốc độ huấn luyện mô hình phân lớp. Nhóm các nghiên cứu sau đây thực hiện huấn luyện mô hình phân lớp từ k láng giềng của phần tử mới x khi phân lớp. Mô hình học của [Bottou & Vapnik, 1992] tìm k láng giềng của phần tử mới x, thực hiện huấn luyện mô hình mạng nơ-ron để phân lớp k láng giềng này, dùng mô hình mạng nơ-ron cục bộ thu được để phân lớp phần tử x. [Vincent & Bengio, 2001] đề xuất giải thuật huấn luyện k siêu phẳng cục bộ (k-local hyperplane). Các nghiên cứu khác về giải thuật SVM cục bộ sử dụng các chiến lược khác nhau cho tìm kiếm k láng giềng, bao gồm SVM-kNN [Zhang et al., 2006] sử dụng các độ đo khoảng cách khác nhau, ALH [Yang & Kecman, 2008] sử dụng khoảng cách có trọng số và chọn lọc các đặc trưng quan trọng, FaLK-SVM [Segata & Blanzieri, 2010] tăng tốc quá trình tìm k láng giềng sử dụng cây chỉ mục cover tree [Beygelzimer et al., 2006]. Đỗ Thanh Nghị, Phạm Nguyên Khang, Trần Nguyễn Minh Thư, Nguyễn Hữu Hòa 207 Nghiên cứu và phân tích lý thuyết về các giải thuật huấn luyện mô hình phân lớp cục bộ được thảo luận trong [Bottou & Vapnik, 1992]. Nghiên cứu chỉ ra có sự dung hòa giữa khả tăng tổng quát của mô hình phân lớp cục bộ và số phần tử được sử dụng để huấn luyện một mô hình phân lớp cục bộ. Kích thước của tập dữ liệu cục bộ được dùng như một tham số tự do bổ sung để điều khiển tính cục bộ và khả năng tổng quát của mô hình phân lớp cục bộ. VI. KẾT LUẬN VÀ HƯỚNG PHÁT TRIỂN Chúng tôi vừa trình bày một giải thuật mới tSVM cho phép huấn luyện nhanh mô hình máy học véc-tơ hỗ trợ cục bộ để phân lớp dữ liệu phi tuyến chính xác cho các tập dữ liệu lớn. Giải thuật tSVM sử dụng máy học cây quyết định để phân hoạch nhanh tập dữ liệu lớn thành k nút lá. Với các nút lá có chứa các phần tử có nhãn không thuần nhất, giải thuật tSVM huấn luyện song song các mô hình SVM phi tuyến, mỗi mô hình để phân lớp cục bộ dữ liệu cho từng nút lá có nhãn không thuần nhất. Kết quả thực nghiệm trên các tập dữ liệu của UCI và 3 tập dữ liệu nhận dạng ký tự viết tay và tập dữ liệu phân lớp ảnh cho thấy giải thuật tSVM cho kết quả phân lớp nhanh, chính xác khi so sánh với giải thuật SVM chuẩn như LibSVM. Một ví dụ về tính hiệu quả của giải thuật tSVM là: thời gian huấn luyện trên tập dữ liệu Forest Cover Types (400.000 phần tử, 54 chiều, 7 lớp) chỉ có 179.8 giây và độ chính xác phân lớp tổng thể 96.73%. Trong thời gian tới, chúng tôi dự định sẽ cung cấp thêm các thực nghiệm trên những tập dữ liệu lớn khác nữa và so sánh hiệu quả của tSVM với các giải thuật học máy khác. Một trong những hướng phát triển của nghiên cứu này trong tương lai là cải tiến độ chính xác phân lớp của tSVM. TÀI LIỆU THAM KHẢO [1] Beygelzimer, A., Kakade, S., Langford, J.: “Cover trees for nearest neighbor”, in proc. of the 23rd intl conf. on Machine learning, pp. 97-104, 2006. [2] Boser, B., Guyon, I., Vapnik, V., “An training algorithm for optimal margin classifiers”, In proceedings of 5th ACM Annual Workshop on Computational Learning Theory, pp.144-152, 1992. [3] Bottou, L., Vapnik, V., “Local learning algorithms”, Neural Computation 4(6): 888-900, 1992. [4] Breiman, L., Friedman, J .H., Olshen, R. A. and Stone, C.: “Classification and Regression Trees”, Wadsworth International, 1984. [5] Chang, C. C., Lin, C. J., “LIBSVM: a library for support vector machines”, ACM Transactions on Intelligent Systems and Technology, vol. 2, no. 27, pp.1-27, 2011 [6] Chang, F., Guo, C. Y., Lin, X. R., Lu, C. J.: “Tree decomposition for largescale SVM problems”, Journal of Machine Learning Research 11:2935-2972, 2010. [7] Collobert, R., Bengio, S., Bengio, Y.: “A parallel mixture of SVMs for very large scale problems”, Neural Computation 14(5):1105-1114, 2002. [8] Cristianini, N., Shawe-Taylor, J., “An Introduction to Support Vector Machines: And Other Kernel-based Learning Methods”, Cambridge University Press, New York, NY, USA, 2000. [9] Dempster, A. P., Laird, N. M., Rubin, D. B.: “Maximum likelihood from incomplete data via the EM algorithm”, Journal of the royal statistical society, series B, vol.39(1):1-38, 1977 [10] Do, T. N., Poulet, F.: “Random local SVMs for classifying large datasets”, in proc. of Intl Conf. on Future Data and Security Engineering 2015 (FDSE 2015), Springer, 2015, pp. 3-15. [11] Do, T. N.: “Non-linear classification of massive datasets with a parallel algorithm of local support vector machines”, in Advanced Computational Methods for Knowledge Engineering Studies in Computational Intelligence, Springer, 2015, pp. 231- 241. [12] Geusebroek, J. M., Burghouts, G. J., Smeulders, A. W. M.: The amsterdam library of object images. Intl Journal Computer Vision 61(1): 103–112, 2005. [13] Gu, Q., Han, J.: “Clustered support vector machines”, in proc. of the Sixteenth Intl Conf. on Artificial Intelligence and Statistics, vol. 31, pp.307-315, 2013. [14] Guyon, I., Web page on svm applications, 1999, [15] Jacobs, R. A., Jordan, M. I., Nowlan, S. J., Hinton, G. E.: “Adaptive mixtures of local experts”, Neural Computation vol.3(1):79-87, 1991. [16] LeCun, Y., Boser, B., Denker, J., Henderson, D., Howard, R., Hubbard, W., Jackel, L.: Backpropagation applied to handwritten zip code recognition. Neural Computation 1(4):541–551, 1989. [17] LeCun, Y., Bottou, L., Bengio, Y., Haffner, P.: Gradient-based learning applied to document recognition. Proceedings of the IEEE 86(11): 2278–2324, 1998. [18] Lichman, M.: UCI machine learning repository, 2013, [19] MacQueen, J.: “Some methods for classification and analysis of multivariate observations”, in proc. of 5th Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, University of California Press 1, pp.281-297, 1967. [20] Osuna, E., Freund, R., Girosi, F., “An improved training algorithm for support vector machines”, Neural Networks for Signal Processing VII, J. Principe, L. Gile, N. Morgan, and E. Wilson Eds, pp.276-285, 1997. [21] Platt, J.: “Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines”, Microsoft Research Technical Report MSR-TR-98-14, 1998. [22] Quinlan, J. R.: “C4.5: Programs for Machine Learning”, Morgan Kaufmann, 1993. 208 GIẢI THUẬT tSVM CHO PHÂN LỚP PHI TUYẾN TẬP DỮ LIỆU LỚN [23] Segata, N., Blanzieri, E.: “Fast and scalable local kernel machines”, Journal Machine Learning Research 11, pp.1883-1926, 2010. [24] Van der Maaten, L.: A new benchmark dataset for handwritten character recognition, 2009, Publications files/characters.zip. [25] Vapnik, V.: “The Nature of Statistical Learning Theory”, Springer-Verlag, 1995. [26] Vincent, P., Bengio, Y.: “K-local hyperplane and convex distance nearest neighbor algorithms”, In Advances in Neural Information Processing Systems, The MIT Press, pp.985-992, 2001. [27] Wu X. and Kumar V.: “Top 10 Algorithms in Data Mining”, Chapman & Hall/CRC, 2009. [28] Yang, T., Kecman, V.: “Adaptive local hyperplane classification”, Neurocomputing vol.71(13-15): 3001-3004, 2008. [29] Yu, H., Yang, J., Han, J.: “Classifying large data sets using SVMs with hierarchical clusters”, In proceedings of the ACM SIGKDD Intl. Conf. on KDD, ACM, pp.306-315, 2003. [30] Zhang, H., Berg, A., Maire, M., Malik, J.: “SVM-KNN: Discriminative nearest neighbor classification for visual category recognition”, In IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Volume 2., pp. 2126-2136, 2006. tSVM ALGORITHM FOR NON-LINEAR CLASSIFICATION OF VERY LARGE DATASETS Thanh Nghi Do, Nguyen Khang Pham, Minh Thu Tran Nguyen, Huu Hoa Nguyen ABSTRACT— In this paper, we present the new support vector machines algorithm, called tSVM for effectively non-linear classification of large datasets. The tSVM algorithm performs the training task of large datasets with two main steps. The first one is to partition the full dataset into k terminal-nodes, and then the second one is to learn in parallel local SVM models for classifying impurity terminal-nodes with mixture of labels. The numerical test results on 4 datasets from UCI repository, 3 benchmarks of handwritten letters recognition and a color image collection of one-thousand small objects show that our tSVM algorithm is efficient compared to the standard SVM (LibSVM) in terms of training time and accuracy for dealing with large datasets.
File đính kèm:
 giai_thuat_tsvm_cho_phan_lop_phi_tuyen_tap_du_lieu_lon.pdf
giai_thuat_tsvm_cho_phan_lop_phi_tuyen_tap_du_lieu_lon.pdf

