Estimation of transmission range of a dual-hop LoRa network under interference effects

)
( )
1
2
, ,
2
, ,
SIR
k
X Y X Y
k i Y i
N
i
Y
X
X Y
P
P
l d h
l d h
=
=

% (4) 
với kk A kN p N = 
% là số lượng ED kích hoạt trong vùng SFk; ( )
2
, ,, ,k i Y i Yl d hP lần lượt là công 
suất phát, hệ số suy hao và độ lợi kênh truyền của nguồn nhiễu ED thứ i từ SFk đến máy thu Y. 
Trong phần 3, khoảng cách truyền dẫn từ S đến G và vị trí trạm lặp sẽ được tính toán dựa 
trên điều kiện ngưỡng của các chỉ số SNR và SIR. 
3. TÍNH CỰ LY TRUYỀN VÀ VỊ TRÍ TRẠM LẶP 
Trong mạng LoRa, một gói hoạt động trong vùng SFo, 7,...,12o được xem là giải mã 
chính xác nếu thỏa mãn đồng thời hai điều kiện sau: 
i) SNR lớn hơn giá trị ngưỡng qo với qo cho trên bảng 1. 
ii) SIR của các gói khác nhau từ cùng một SF hoặc từ các SF khác phải lớn hơn giá trị 
ngưỡng ∆𝑜,𝑘 (dB) với 𝑜, 𝑘 ∈ {7, ,12} [12]. Giá trị ∆𝑜,𝑘 là phần tử thuộc hàng o và cột k được 
Transport and Communications Science Journal, Vol 72, Issue 3 (04/2021), 264-276 
270 
lấy trong ma trận sau: 
 
 SF SF SF SF SF SF
7 8 9 10 11 12
SF 1 8 9 9 9 97
SF 11 1 11 12 13 138
SF 15 13 1 13 14 159
19 18 17 1 17 18SF
10
22 22 21 20 1 20SF
11
25 25 25 24 23 1SF
12
dB
− − − − −
− − − − −
− − − − −
− − − − −
− − − − −
− − − − −
 =
 (5) 
3.1. Tính cự ly truyền tối đa khi có trạm lặp 
Để tính cự ly truyền tối đa khi có trạm lặp thì vị trí trạm lặp, S và G phải thỏa mãn các 
điều kiện sau: 
• Điều kiện đảm bảo SNR ngưỡng 
 , ,SNRS R S Rq và SNRRG oq (6) 
do S luôn ở vị trí xa nhất của mạng nên ,S Rq luôn là 12q , vị trí R đang xét có thể thay đổi 
ở một trong các vùng SF đặt nên 
oq thay đổi. 
• Điều kiện đảm bảo ngưỡng SIR 
✓ Ngưỡng SIR do nhiễu trong cùng SF co-SF 
 , ,SIR
co SF co SF
S R S R
− − và , ,SIR
co SF co SF
R G R G
− − (7) 
SIR của 2 chặng đều phải lớn hơn ngưỡng, giá trị ,
co SF
X Y
− , ,X S R , ,Y R G tùy thuộc 
vào vùng gói dữ liệu được gửi đi; hơn nữa ,
co SF
X Y
− cũng là thành phần đường chéo trong ma trận 
 . Ví dụ nếu gói gửi từ S ở vùng SF12 thì , 12,12
co SF
S R
− = , tương tự với chặng thứ hai có 
, ,
co SF
R G o o
− = với 7, ,12o K . 
✓ Ngưỡng SIR do nhiễu từ các SF khác inter-SF 
inter inter
, ,SIR
SF SF
S R S R
− − và 
inter inter
, ,SIR
SF SF
R G R G
− − (8) 
các giá trị 
i nter
,
SF
X Y
− tùy thuộc vào SF của gói muốn nhận và gói nhiễu, ta có 
 i nter, 12, , 7,...,11
SF
S R k k
− = và i nter, , , ; , 7,...,12
SF
R G o k k o o k
− = 
✓ Ngưỡng SIR do cả nhiễu co-SF khác inter-SF 
, ,SIR
both both
S R S R và , ,SIR
both both
R G R G (9) 
các giá trị SIR cần đảm bảo cả ngưỡng co-SF và inter-SF từ S đến R và từ R đến G, các giá 
trị ngưỡng , 12, , 7,...,12
both
S R k k = và 
i nter
, , , 7,...,12
SF
R G o k k
− = 
Chương trình findDmaxWithRelay thực hiện tìm cự ly truyền tối đa (max)SGD giữa S và G 
và vị trí trạm lặp tương ứng _ (max)R kx được mô tả theo đoạn mã giả dưới đây với các tham số 
Tạp chí Khoa học Giao thông vận tải, Tập 72, Số 3 (04/2021), 264-276 
271 
được mô tả trong Bảng 2. 
Bảng 2. Tham số trong chương trình findDmaxWithRelay. 
Ký hiệu 
tham số 
Ý nghĩa 
_R kx Vị trí trạm lặp với k chạy để  (max)_ ,c RR kx d x 
cd , Rx và SGD Lần lượt là vị trí ngắn nhất, bước tăng của Rx và SGD trong vòng for 
, (max)SG kD Cự ly truyền tối đa tại vị trí trạm lặp _R kx 
(max)SGD Cự ly truyền lớn nhất trong các , (max)SG kD và vị trí trạm lặp tương ứng _ (max)R kx 
PROCEDURE findDmaxWithRelay 
Begin 
xR = dc; 200m
Rx
 = ; 200m
SGD
 = ; ( )max 10 ;RSG x RD x= 
SGD =[]; % ma trận rỗng 
for xR_k = dc to xR (max) 
  ,SG kD = ; % ma trận rỗng 
 for ( _ )_RSG x k m cD d= to ( )maxRSG xD 
 if ( , ,SNRS R S Rq and SNRRG oq and , ,SIR
both both
S R S R and , ,SIR
both both
R G R G ) 
 _ ,SG k mD = ( _ )_RSG x k mD ; 
 else if 
 _ ,SG k mD = 0; 
 endif 
, , , ,,SG k SG k SG k mD D D = ; % ghép ma trận 
 endfor 
 , (max) _max ( );SG k SG kD D= % cự ly lớn nhất với vị trí trạm lặp _xR k 
, (max),SG SG SG kD D D = ; % ghép ma trận 
endfor 
(max) max( )SG SGD D= ; 
end 
3.2. Tính vị trí trạm lặp để đảm bảo cự ly truyền nhất định 
Để quy hoạch mạng thuận tiện hơn, bài báo xây dựng chương trình findRelayLocation thực 
hiện các vị trí đặt trạm lặp với một cự ly truyền xác định DSG, tập kết quả trả về là các vị trí 
trạm lặp Rx thỏa mãn các điều kiện về SNR và SIR như trong công thức (7) và (9). Thuật toán 
như sau: 
PROCEDURE findRelayLocation 
Begin 
200
Rx
m = ; xR (max) = DSG – dc 
xR = []; % ma trận rỗng 
Transport and Communications Science Journal, Vol 72, Issue 3 (04/2021), 264-276 
272 
for xR_k = dc to xR (max) 
 if ( , ,SNRS R S Rq and SNRRG oq and , ,SIR
both both
S R S R and , ,SIR
both both
R G R G ) 
 _[ , ];R R R kx x x= % ghép ma trận 
 endif 
 endfor 
 End 
3.3. Tính cự ly truyền tối đa khi không có trạm lặp 
Để so sánh hiệu quả của việc sử dụng trạm lặp trong việc mở rộng phạm vi truyền của 
mạng LoRa phần này sẽ tính cự lý truyền tối đa khi không dùng trạm lặp. Cự ly truyền tối đa 
khi không có trạm lặp DSG(max) là cự ly lớn nhất mà tại đó thỏa mãn các điều kiện sau: 
• Điều kiện đảm bảo SNR ngưỡng: 
 , ,SNRS G S Gq (10) 
do S luôn ở vị trí xa nhất của mạng nên ,S Gq luôn là 12q . 
• Điều kiện đảm bảo ngưỡng SIR cho cả nhiễu co-SF và inter-SF: 
 , ,SIR
both both
S G S G (11) 
 với , 12, , 7,...,12
both
S G k k = 
 Chương trình findDmaxWithoutRelay thực hiện tìm DSG(max) được mô tả theo đoạn mã giả 
dưới đây với 
cd là cự lý tối thiểu xét, SG là bước tăng dần DSG khi thỏa mãn các điều kiện về 
SNR và SIR, cờ flag=0 khi các điều kiện SNR và SIR không còn thỏa mãn và cự ly đã đạt tối 
đa. 
PROCEDURE findDmaxWithoutRelay 
Begin 
DSG = dc ; flag =1; 200SG m = ; 
while (flag) 
if ( , ,SNRS G S Gq and , ,SIR
both both
S G S G ) then 
DSG = DSG + SG ; 
 else 
 DSG (max) = DSG ; flag =0; 
 end if 
end while 
End 
4. KẾT QUẢ MÔ PHỎNG 
Phần này đưa ra các kết quả mô phỏng tính toán cự ly truyền tối đa và vị trí trạm lặp cho 
mạng LoRa với mô hình mạng như hình 1 và kịch bản có trạm lặp và không có trạm lặp thông 
qua mô phỏng Monte Carlo. Các thông số mô phỏng được thực hiện với 250 KHz,BW = 
3, = 868 MHz,cf = 10 byte,pacL = 60sinT = , ED=10
3 và 4 / 5. CR = 
Hình 2 thể hiện kết quả khảo sát SNR giữa S và G khi không sử dụng trạm lặp. Căn cứ vào 
kết quả trên ta thấy nếu không xét đến nhiễu SIR mà chỉ xét đến điều kiện SNR thì cự ly tối đa 
Tạp chí Khoa học Giao thông vận tải, Tập 72, Số 3 (04/2021), 264-276 
273 
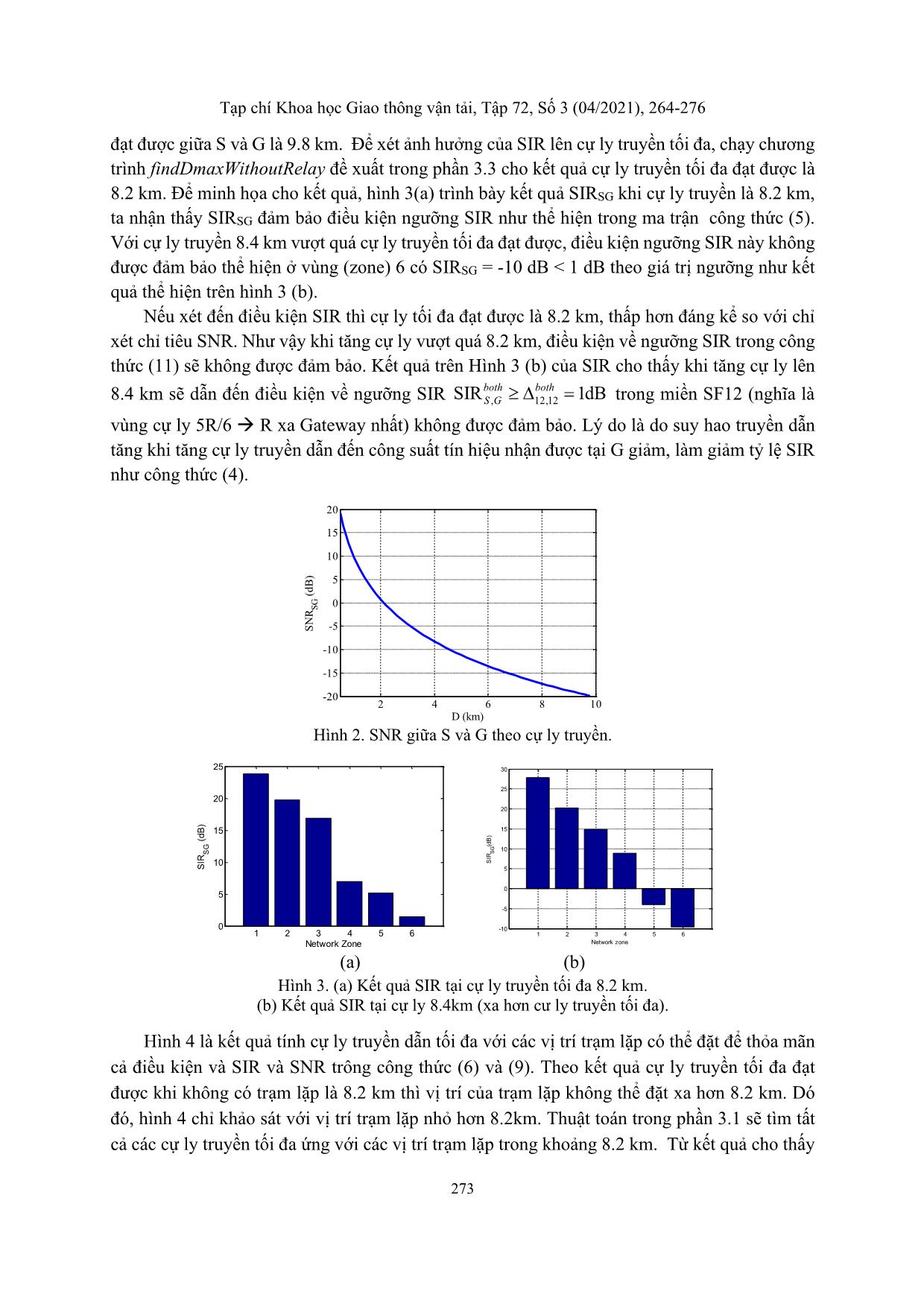
đạt được giữa S và G là 9.8 km. Để xét ảnh hưởng của SIR lên cự ly truyền tối đa, chạy chương 
trình findDmaxWithoutRelay đề xuất trong phần 3.3 cho kết quả cự ly truyền tối đa đạt được là 
8.2 km. Để minh họa cho kết quả, hình 3(a) trình bày kết quả SIRSG khi cự ly truyền là 8.2 km, 
ta nhận thấy SIRSG đảm bảo điều kiện ngưỡng SIR như thể hiện trong ma trận công thức (5). 
Với cự ly truyền 8.4 km vượt quá cự ly truyền tối đa đạt được, điều kiện ngưỡng SIR này không 
được đảm bảo thể hiện ở vùng (zone) 6 có SIRSG = -10 dB < 1 dB theo giá trị ngưỡng như kết 
quả thể hiện trên hình 3 (b). 
Nếu xét đến điều kiện SIR thì cự ly tối đa đạt được là 8.2 km, thấp hơn đáng kể so với chỉ 
xét chỉ tiêu SNR. Như vậy khi tăng cự ly vượt quá 8.2 km, điều kiện về ngưỡng SIR trong công 
thức (11) sẽ không được đảm bảo. Kết quả trên Hình 3 (b) của SIR cho thấy khi tăng cự ly lên 
8.4 km sẽ dẫn đến điều kiện về ngưỡng SIR , 12,12SIR 1dB
both both
S G = trong miền SF12 (nghĩa là 
vùng cự ly 5R/6 → R xa Gateway nhất) không được đảm bảo. Lý do là do suy hao truyền dẫn 
tăng khi tăng cự ly truyền dẫn đến công suất tín hiệu nhận được tại G giảm, làm giảm tỷ lệ SIR 
như công thức (4). 
Hình 2. SNR giữa S và G theo cự ly truyền. 
(a) (b) 
Hình 3. (a) Kết quả SIR tại cự ly truyền tối đa 8.2 km. 
(b) Kết quả SIR tại cự ly 8.4km (xa hơn cư ly truyền tối đa). 
Hình 4 là kết quả tính cự ly truyền dẫn tối đa với các vị trí trạm lặp có thể đặt để thỏa mãn 
cả điều kiện và SIR và SNR trông công thức (6) và (9). Theo kết quả cự ly truyền tối đa đạt 
được khi không có trạm lặp là 8.2 km thì vị trí của trạm lặp không thể đặt xa hơn 8.2 km. Dó 
đó, hình 4 chỉ khảo sát với vị trí trạm lặp nhỏ hơn 8.2km. Thuật toán trong phần 3.1 sẽ tìm tất 
cả các cự ly truyền tối đa ứng với các vị trí trạm lặp trong khoảng 8.2 km. Từ kết quả cho thấy 
2 4 6 8 10
-20
-15
-10
-5
0
5
10
15
20
D (km)
S
N
R
S
G
 (
d
B
)
1 2 3 4 5 6
0
5
10
15
20
25
Network Zone
S
IR
S
G
 (
d
B
)
1 2 3 4 5 6
-10
-5
0
5
10
15
20
25
30
Network zone
S
IR
S
G
(d
B
)
Transport and Communications Science Journal, Vol 72, Issue 3 (04/2021), 264-276 
274 
cự ly tối đa của mạng LoRa đạt 12.72 km tại ví trí trạm lặp xR = 6.6 km. Kết quả này tăng lên 
đáng kể so với cự ly 8.2 km không dùng trạm lặp. Tại vị trí xR = 7 km, khi ta khảo sát đến 
DSG > 10 km thì điều kiện ngưỡng (cho chặng RG, lúc này có dRG > 3 km) không thỏa 
mãn nữa nên cự ly truyền lớn nhất DSG là 10 km. Cần lưu ý rằng tại bất kỳ khoảng cách 
nào thì mô hình mạng vẫn tuân theo hình 1, nên các kết quả không chỉ xét đến cự ly mà 
còn xét đến vị trí trạm lặp đang thuộc SF nào ứng với cự ly đó như trong bảng 1. Vị trí 
của trạm lặp càng gần G thì công suất phát càng thấp và mức ngưỡng qo càng cao. Phân 
tích cụ thể hơn kết quả trên Hình 4 ta nhận thấy, khi tăng vị trí đặt trạm lặp quá xa S ( nghĩa là 
xR > 6.6 km) thì suy hao truyền dẫn từ S đến R sẽ lớn làm giảm công suất tín hiệu hiệu có ích 
dẫn đến ảnh hưởng của co-SF và inter-SF nghiêm trọng hơn nên giảm cự ly truyền tối đa đạt 
được, và khi xR > 7.8 km thì điều kiện ngưỡng SIR không còn thỏa mãn. 
Để làm rõ ảnh hưởng của nhiễu co-SF và inter-SF, Hình 5 là kết quả cự ly truyền tối đa 
nếu chỉ xét điều kiện về SNR như trong công thức (6), nghĩa là không xét đến nhiễu co-SF và 
inter-SF. Kết quả cho thấy nhiễu co-SF và inter-SF không gây ảnh hưởng nhiều đến cự ly truyền 
tối đa nhưng ảnh hưởng đến vị trí đặt trạm lặp do khi tăng vị trí đặt trạm lặp quá xa S thì suy 
hao truyền dẫn từ S đến R lớn làm giảm công suất thu được tại R dẫn đến ảnh hưởng của co-
SF và inter-SF nghiêm trọng hơn. Nếu chỉ xét đến điều kiện ngưỡng SNR, có thể đặt vị trí trạm 
lặp lên tới 9.8 km so với 7.8 km khi xét đến ảnh hưởng của cả nhiễu co-SF và inter-SF. 
Hình 4. Cự ly truyền dẫn tối đa với các vị trí đặt trạm lặp khác nhau xét cả điều kiện SIR và SNR. 
Tạp chí Khoa học Giao thông vận tải, Tập 72, Số 3 (04/2021), 264-276 
275 
Hình 5. Cự ly truyền dẫn tối đa với các vị trí đặt trạm lặp khác nhau chỉ xét điều kiện ngưỡng SNR. 
Hình 6. Kết quả SNR với các vị trí đặt trạm lặp khác nhau ở cự ly truyền 10 km. 
Hình 6 là kết quả SNR với các vị trí đặt trạm lặp khác nhau ở cự ly truyền 10 km. Để đảm 
bảo điều kiện ngưỡng SNR trong (6) thì vị trí trạm lặp có thể đặt trong khoảng từ 5 km đến 
9.8km. Tuy nhiên, nếu xét đến điều kiện SIR trong công thức (6) thì vị trí trạm lặp có thể đặt 
trong khoảng từ 5 km đến 6.17 km so với S. Tương tự, áp dụng với cự ly truyền 12 km thì vị 
trí trạm lặp có thể đặt ở vị trí từ 6 km đến 8 km so với S. 
5. KẾT LUẬN 
Bài báo đã sử dụng cấu hình mạng LoRa gồm 6 vùng SFk và mô hình kênh truyền Rayleigh 
để phân tích tín hiệu cũng như tính toán các chỉ số chất lượng hệ thống gồm SNR, SIR. Căn cứ 
vào các điều kiện ngưỡng SNR và SIR của mạng LoRa xét trong cùng một vùng SF (co-SF) và 
giữa các vùng SF (inter-SF), cự ly truyền dẫn tối đa và vị trí trạm lặp được tính toán. Các kết 
quả cho thấy việc đặt thêm trạm lặp ở vị trí phù hợp có thể mở rộng phạm vi truyền của mạng 
LoRa. Các kết quả và thuật toán đề xuất trong bài báo có thể áp dụng trong quá trình quy hoạch 
và thiết kế mạng LoRa ban đầu trước khi triển khai thực tế. 
LỜI CẢM ƠN 
Nghiên cứu này được tài trợ bởi Trường đại học Giao thông vận tải trong đề tài mã số 
T2020-DT-004. 
Tác giả xin chân thành cảm ơn Công ty cổ phần thiết bị quan trắc địa kỹ thuật và môi trường 
Việt Nam đã hỗ trợ trong quá trình thực hiện nghiên cứu thực nghiệm. 
TÀI LIỆU THAM KHẢO 
[1]. A. Mahmood et al., Scalability Analysis of a LoRa Network Under Imperfect Orthogonality, IEEE 
Transactions on Industrial Informatics, 15 (2019) 1425-1436. https://doi.org/10.1109/TII.2018.2864681 
[2]. R. El Chall, S. Lahoud, M. El Helou, LoRaWAN Network: Radio Propagation Models and 
Performance Evaluation in Various Environments in Lebanon, IEEE Internet of Things Journal, 6 
(2019) 2366-2378. https://doi.org/10.1109/JIOT.2019.2906838 
[3]. Orestis Georgiou, Usman Raza, Low Power Wide Area Network Analysis: Can LoRa Scale?, IEEE 
Wireless Communications Letters, 6 (2017) 162-165. https://doi.org/10.1109/LWC.2016.2647247 
Transport and Communications Science Journal, Vol 72, Issue 3 (04/2021), 264-276 
276 
[4]. D. Bankov, E. Khorov, A. Lyakhov, Mathematical model of LoRaWAN channel access with capture 
effect, 2017 IEEE 28th Annual International Symposium on Personal, Indoor, and Mobile Radio 
Communications (PIMRC), 2017, pp. 1-5. https://doi.org/10.1109/PIMRC.2017.8292748 
[5]. D. Croce et al., Impact of LoRa Imperfect Orthogonality: Analysis of Link-Level Performance, 
IEEE Communications Letters, 22 (2018) 796-799. https://doi.org/10.1109/LCOMM.2018.2797057 
[6]. Lain-Chyr Hwang et al., A bridge between the smart grid and the Internet of Things: Theoretical 
and practical roles of LoRa, International Journal of Electrical Power & Energy Systems, 113 (2019) 
971-981. https://doi.org/10.1016/j.ijepes.2019.06.001 
[7]. H. Lee, K. Ke, Monitoring of Large-Area IoT Sensors Using a LoRa Wireless Mesh Network 
System: Design and Evaluation, IEEE Transactions on Instrumentation and Measurement, 67 (2018) 
2177-2187. https://doi.org/10.1109/TIM.2018.2814082 
[8]. J. Petajajarvi et al., On the coverage of LPWANs: range evaluation and channel attenuation model 
for LoRa technology, 14th International Conference on ITS Telecommunications (ITST), 2015, pp. 55-
59. https://doi.org/10.1109/ITST.2015.7377400 
[9]. P. A. Campos et al., Evaluation of LoRaWAN Transmission Range for Wireless Sensor Networks 
in Riparian Forests, 22nd International ACM Conference on Modeling, 2019, pp. 199-206. 
https://doi.org/10.1145/3345768.3355934 
[10]. T. H. Nguyen et al., Performance Analysis and Optimization of the Coverage Probability in Dual 
Hop LoRa Networks With Different Fading Channels, IEEE Access, 8 (2020) 107087-107102. 
https://doi.org/10.1109/ACCESS.2020.3000600 
[11]. L. Parri et al., Offshore LoRaWAN Networking: Transmission Performances Analysis Under 
Different Environmental Conditions, IEEE Transactions on Instrumentation and Measurement. Early 
Access, 2020, pp. 1-1. https://doi.org/10.1109/TIM.2020.3031193 
[12]. A. Hoeller et al., Analysis and Performance Optimization of LoRa Networks With Time and 
Antenna Diversity, IEEE Access, 6 (2018) 32820-32829. https://doi.org/ 
10.1109/ACCESS.2018.2839064